玻化微珠保温砂浆导热系数模型研究*
龚建清,张婵韬
(湖南大学 土木工程学院,湖南 长沙 410082)
玻化微珠保温砂浆导热系数模型研究*
龚建清†,张婵韬
(湖南大学 土木工程学院,湖南 长沙 410082)
基于最小热阻力法则和均匀化方法估算了玻化微珠保温砂浆的等效导热系数.用ANSYS模拟玻化微珠保温砂浆二维单元胞体的热传导,发现对热阻网络的横向热阻的极端考虑会给计算结果带来误差.用ANSYS计算的三维单元体模型的等效导热系数值与3种理论计算值进行比较,发现用假设横向热阻无穷小与假设横向热阻无穷大求得的单元体等效热阻的平均值作为单元体的等效热阻来求单元体等效导热系数更精确,最后实验也验证了这一结论.实验值与本文提出的理论模型计算值偏差仅为0.2%,证明用该方法来估算玻化微珠保温砂浆的导热系数是可行的.
最小热阻力;均匀化方法;等效导热系数;玻化微珠保温砂浆;有限元模拟
玻化微珠保温砂浆作为建筑节能领域的一种保温材料,除其物理力学性能应满足一定要求外,更重要的是其保温性能应满足节能的要求.导热系数是衡量玻化微珠保温砂浆保温性能最主要的技术性能指标,它的大小直接决定着玻化微珠保温砂浆的品质及工程项目的节能效果.因此,对玻化微珠保温砂浆的导热机理进行研究,并建立理论计算模型,对研究其保温性能至关重要.
目前,国内对玻化微珠保温砂浆的研究主要集中在从其组成材料及施工工艺方面进行创新、改进,提高其各项工作性能这些方面[1-6],针对玻化微珠保温砂浆导热机理的研究很少见,导热系数理论计算模型也很少.
玻化微珠保温砂浆是一种无机复合材料,国际上常用来计算复合材料等效导热系数的方法主要有3种——理论分析法、数值模拟计算法和实验研究法.理论分析法应用得最多的是 Maxwell-Eucken方程及其一系列改进方程[7-12],这类方法简单,应用范围广;数值计算法用得最多的是有限元法和有限差分法[13-14].这类方法简单、直观,在一定范围内能够给出与实验相符合的结果.但是所得结果只能以曲线或图表方式给出,或以经验公式的形式给出,一般说来无法将其表达为材料微结构几何和各组分体积分数的函数.实验研究的方法通常是通过对特定材料的导热系数进行研究,得到其中的规律,从而归纳出经验公式.此种方法针对特定材料求导热系数是最可靠的,但是却无法普及到其他材料的应用中去[15].
本研究选择了一种理论分析法:运用均匀化方法,建立一个玻化微珠保温砂浆的单元胞体,基于最小热阻力法则推导出单元胞体横向热阻无穷大和横向热阻无穷小2种热阻网络等效导热系数理论计算公式,2种热阻网络计算结果相差较大.用有限元软件ANSYS,模拟根据稳态导热原理建立起来的防护热板法,研究玻化微珠保温砂浆二维单元胞体的热传导,发现对横向热阻的极端考虑会带来较大误差.因此本研究用2种热阻网络的平均热阻作为单元体的等效热阻来计算单元体等效导热系数,得出的结果与ANSYS模拟值及实测值的偏差均比前两者小.本研究论证了该理论计算模型与玻化微珠保温砂浆的适用性及该模型的可靠性,为玻化微珠保温砂浆的配比研究提供了一条新途径.
1 实验
1.1 实验原料
湖南韶峰水泥集团有限公司生产的普通硅酸盐水泥,P.O42.5;信阳市中凯保温材料有限公司生产的玻化微珠,堆积密度80~100kg/m3,干表观密度160kg/m3,导热系数0.032W/(m·K);外加剂采用自配复合外加剂:耒阳市洪波灰渣有限公司生产的干排二级粉煤灰,密度2.34g/cm3;石家庄市隆瑞建筑材料有限公司生产的可再分散性乳胶粉LR-80,堆积密度500g/L±50g/L;河北华艺纤维素有限公司生产的羟丙基甲基纤维素;广州杜科建材有限公司生产的DUK-A2型聚丙烯纤维,长度19 mm.试验材料的配比见表1.

表1 水泥基体材料配比Tab.1 Mixture proportion of cement matrix
1.2 配方设计及试块制作
分别按照玻化微珠骨料体积掺量占硬化后试块总体积分数的0%,10%,20%,30%和40%共5个水平制作试块,每个水平制作试块2个,尺寸为300mm×300mm×30mm.1个试块的玻化微珠掺量mc=ρkV,式中ρ为玻化微珠干表观密度,k为玻化微珠骨料体积掺量占硬化后试块的总体积分数,V为一个试块的体积.制作好的试块用聚乙烯薄膜覆盖成型后放在养护室内2d,脱模后再到标准养护箱(温度20℃,相对湿度60%)中养护至28d.
1.3 实验方法
试样导热系数的测试参照GBT 10294—2008(《绝热材料稳态热阻及有关特性的测定——防护热板法》).导热系数测定仪为沈阳紫微机电设备有限公司生产的CD-DR3030型导热系数测定仪.
1.4 结果
实验测得不同骨料掺量玻化微珠保温砂浆导热系数实验值见表2.

表2 不同骨料掺量玻化微珠保温砂浆导热系数实验值Tab.2 Experimental values of thermal conductivity of hollow beads insulating mortar with different aggregate content
从表2中可以看出,随着玻化微珠体积掺量的增加,导热系数下降.
2 模型的建立
玻化微珠保温砂浆的组成很复杂,包括骨料、胶凝材料、纤维增强剂、外加剂、改性剂等多种组分.大量的研究表明[16-17],当玻化微珠保温砂浆组分固定时,影响其导热系数的主要因素为玻化微珠骨料的掺量.因此,本研究将由各种胶凝材料及外加剂组成的水泥基体看成一个相,那么就可以把玻化微珠保温砂浆作为一种由水泥基体和玻化微珠颗粒组成的两相无机复合材料,来研究其导热性能.
2.1 理论基础
最小热阻力法则:热量在物体内传递时,热流会沿热阻最小的通道传递,相应通道的总热阻为最小热阻.热阻力(ΔT)即为热流量q流过热阻为R的通道时所消耗的温降:

傅立叶定律:对于物性参数不随方向变化的各向同性物体,导热热流密度矢量与温度梯度之间的关系为:

式中:q为热流量,表示单位时间内通过单位面积的热量;λ为导热系数,表示在单位时间内每单位温度降低时,每单位面积所通过的热量,是直接表征物质导热能力的一个重要物理量.

式中:q为单位时间内通过面积A的总热量;ΔT表示温度与沿导热方向L深度处温度的差值.由式(1)(3)可得均质材料热阻

式中:L为热流通道的长度;A为热流通道的面积;λ为通道材料的导热系数.对于复合材料,我们要引入2个新概念——等效热阻(Re)和等效导热系数(λe).等效热阻为1W热量通过复合材料时所引起的温升.等效导热系数则是在稳定传热条件下,1m厚的复合材料,两侧表面的温差为1℃,在1s内,通过1m2面积传递的热量.按式(4)则有:

因此,复合材料的导热系数可通过计算等效热阻得来.
均匀化方法:利用均匀化方法可以建立起研究单元体与复合材料总体之间的关系.该方法的思路为:从非均质材料中选取一个具有代表性的单胞,单胞的平均性质可以作为材料宏观性质的表征.
2.2 单元体的建立
根据玻化微珠保温砂浆的特点,作以下假设:
1)玻化微珠颗粒以相同大小的球体均匀分布于水泥基体中;
2)由于玻化微珠内空腔的直径远小于4mm,故在空腔内的热对流是可以忽略的[18];
3)由于使用温度不高,辐射相对于总传热来说很小,故辐射传热忽略不计[19];
4)虽然玻化微珠的单胞粒子在微观上呈现不均匀性,但其尺寸远小于复合材料的宏观尺寸,为此在宏观上可认为具有各向同性.
由于假定玻化微珠粒子在水泥基体中均匀分布,整个复合材料可以考虑为一系列单元连接而成,而每个单元是由水泥基体包含着一个玻化微珠粒子的立方体,如图1所示.

图1 玻化微珠保温砂浆导热物理模型的建立过程Fig.1 The process of modeling heat conduction of hollow beads insulating mortar
根据均匀化方法,复合材料的等效导热系数可以考虑为在相应温度下一个单元的等效导热系数.
2.3 理论公式的推导
为了求得单元体等效热阻,可以把复合物单元体分割成数量足够多的等尺度微元块,根据式(4)算出微元块的平均热阻.微元块间的连接抽象为微元块热阻之间的连接,单元体的等效热阻就等于热阻网络的总热阻.
根据横向(垂直于热流的方向)热阻的不同,热阻网络可以分成两种极端的形式,如图2所示.

图2 两种热阻网络图Fig.2 Two kind of resistance network
图2(a)是假设横向热阻为无穷大,各热阻横向间不会有热传递,在平行于热流方向进行微层处理,则单元体热流通道被分成两大部分:第一部分是在热流主向上只有连续相的通道;第二部分是在热流主向上会遇到球形分散相的通道,在该通道内,根据热阻率相等的原则,以过球心的热流线为轴,取微元环形通道,各通道热阻并联,遇到球形分散相的通道热阻由分散相和连续相串联组成.
先分别求得各部分等效热阻.

式中:λ1,λ2分别为分散相球体和连续相的导热系数;θ为球半径与轴线的夹角;r为分散相球体的半径;rcosθdθ为半径r与轴线夹角θ处圆筒环的筒壁厚.
第二部分由许多微环通道的热阻并联构成,可以用并联热阻倒数求和得到总热阻.第一部分和第二部分同样是并联关系,所以单元体总热阻由各热流通道热阻并联得到:

图2(b)是假设横向热阻为无穷小,温度沿热流的方向呈线性分布.在垂直于热流方向进行微层处理,则单元体可以分为2大部分:第一部分只含连续相;第二部分含有分散相和连续相,第一部分和第二部分各层串联组成,第二部分各层由分散相和连续相并联组成.
各部分热阻由傅立叶定律求得.

式中:λ1和λ2分别为分散相球体和连续相的导热系数;r为分散相球体的半径;dx为x处薄层的厚度.
2.4 基于最小热阻力法则模型的计算结果与分析
按照以上2种模型的计算公式,分别求分散相体积分数为10%,20%,30%,40%的计算值.
玻化微珠是表面玻化封闭的球状体颗粒,内部为多孔空腔结构,空腔直径约50~100μm.真正起隔热作用的正是这些微小的空腔,即使玻化微珠颗粒粒径不同,内部空腔的大小变化也十分微小,只要分散相掺量不变,则空腔总量变化也非常小,因此本文忽略颗粒大小对导热系数的影响,根据分散相的体积分数来求分散相的等效半径:设单元体是边长为l的正方体,分散相等效半径为r,分散相的体积分数为v,则

λ1和λ2分别取0.032W/(m·K)和0.93W/(m·K).将式(16)及λ1和λ2分别代入式(11)和式(15),得到的结果如图3所示.
从图3中可以看出,基于最小热阻力法则建立的2种模型,随着玻化微珠粒子掺量的增加,2种计算模型的计算值都逐渐降低,这和已有研究结果一致[3,7].横向热阻无穷小模型的计算值均高于横向热阻无穷大模型,且随着玻化微珠掺量的增加,这种趋势越来越明显.可见单元体热阻网络的划分方式对等效导热系数的计算值有很大的影响.

图3 2种热阻网络模型计算结果对比Fig.3 The comparison of calculation result of two kind of resistance network model
3 有限元模拟

本文用有限元软件模拟了根据稳态导热原理传热建立起来的防护热板法,建立了一个三维的单元体热传导模型,如图4所示.四边绝热,热流从顶面输入.
3.1 二维单元传热模拟
考虑到玻化微珠颗粒在水泥基体中均匀分布,且三维模型是完全对称的,所以将三维温度场简化
近年来,用数值法来解传热问题越来越普遍,常用的主要有有限元法、有限差分法及边界元法.本研究采用的是有限元法,应用ANSYS软件进行单元体的传热数值模拟.
国际上用来测量导热系数的方法有2两种:稳态法和非稳态法.2种方法的各种形式都各有特点和适用条件.根据稳态导热原理建立起来的方法在国内外已很成熟.20世纪80年代末,我国已参照国际标准制定了一系列国家标准.根据该原理制作的测试装备主要有防护热板法和圆球法导热系数测定仪.防护热板法的试样最容易制作,而且平行的等温面比较容易实现、操作也方便,因此被广泛采用.防护热板装置的原理如下:在具有平行表面的均匀板状试件内,建立类似于以2个平行的温度均匀的平面为界的无限大平板中存在的一维均匀热流密度.平板导热仪由热板、冷板和护板3部分组成.热的流动方向从热板流向冷板,当温度达到恒定后,测量冷热板的温差(ΔT)、两板之间的距离L及从热板传输的热流量q,根据傅立叶稳态热传导规律,即可求出单元体等效导热系数:为二维.二维模型更易看清楚单元体温度梯度的变化,以及热流的方向.

图4 单元体示意图Fig.4 Sketch of unit
单元各边设定的边界条件如下:
左右两边为绝热边,顶边施加第一类边界条件:恒温载荷30℃;底边施加第二类边界条件:对流载荷,环境温度取25℃,对流传热系数取25W/(m2·°C).使用求解器进行求解,然后进入后处理,得到单元的温度云图(图5)和热流矢量图(图6).
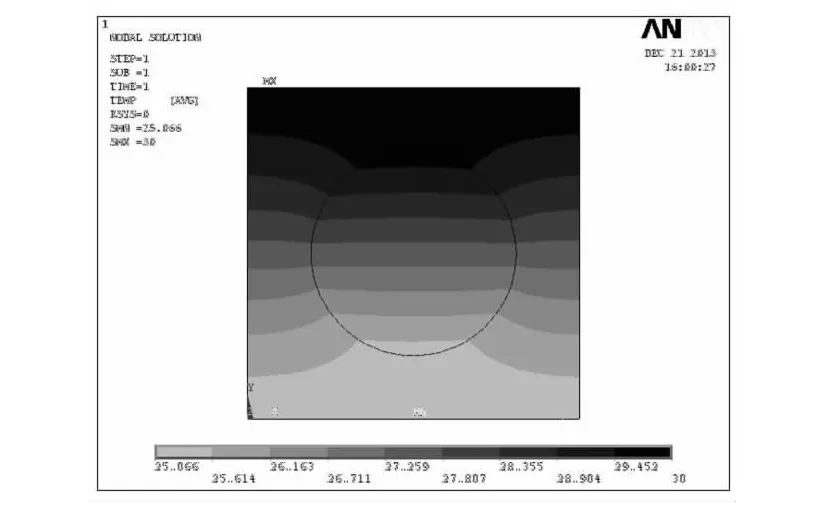
图5 单元温度云图Fig.5 Temperature nephogram of unit
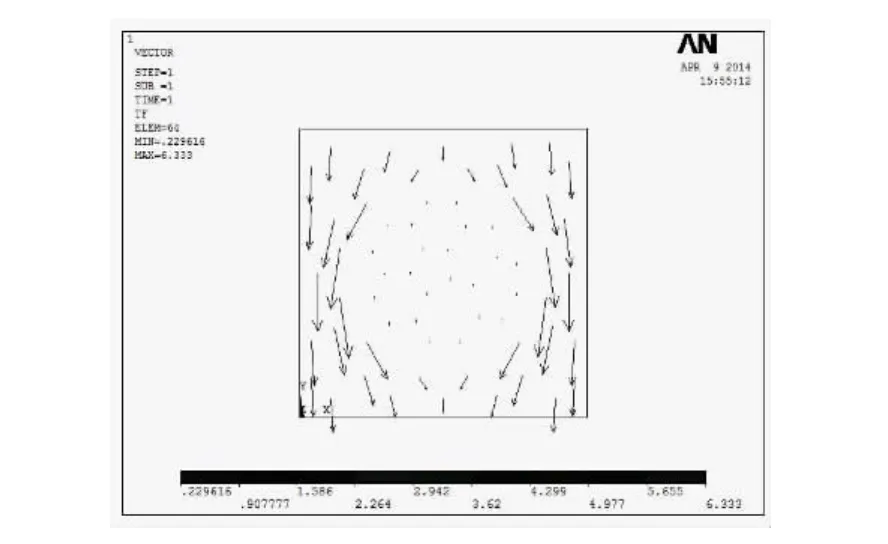
图6 单元热流矢量图Fig.6 Heat flux vector diagram of unit
热流矢量图反映了单元内热流的方向及大小,箭头的方向代表热流的方向,箭头的长短代表热流的强弱.很明显,热流的方向并不是都沿着单元体的轴线方向.大部分遇到分散相的热流,方向不再是沿着轴线方向,而是发生了偏转.因此假设横向热阻无穷大,或者假设横向热阻无穷小都与实际不符,从而使理论计算值产生一定偏差.
如果要得到更高精度的单元体等效导热系数值,必须考虑横向热阻.横向热阻的大小为单元体等效导热系数值.文献[20]对简单的热阻网络进行过计算,发现用横向热阻无穷大模型的等效热阻和横向热阻无穷小模型的等效热阻的算术平均值来作为单元体的等效热阻的近似值仅比用实际的单元体等效热阻作为横向热阻进行迭代得到的单元体等效热阻精确值小0.2%.因此,本文用横向热阻无穷大模型的等效热阻和横向热阻无穷小模型的等效热阻的算术平均值作为单元体的等效热阻,求得单元体的等效导热系数为:


3.2 等效导热系数数值计算
为了得到较精确的计算机模拟值,本研究采用与理论计算模型一致的三维单元体模型.用与二维模型热传导模拟类似的步骤进行求解.得到上下边的温差ΔT及热流量q.利用式(17),分别计算出了玻化微珠保温砂浆复合体系,玻化微珠填充体积分数为10%,20%,30%和40%时相应的单元体的等效导热系数.并将横向热阻无穷小模型的等效导热系数理论公式计算值(λe-bc)、横向热阻无穷大模型的等效导热系数理论公式计算值(λe-cb)以及本文提出的用2种模型等效热阻的算术平均值作为单元体等效热阻求得的单元体等效导热系数(λe)与计算机模拟值进行对比,结果见表3.

表3 理论公式计算值与计算机模拟值比较Tab.3 Comparison between theoretical formula values and computer simulation values
从表3中可以看出,λe-bc,λe-cb与计算机模拟值的平均偏差均大于λe与计算机模拟值的平均偏差,这初步证明了采用本文提出的用2种模型等效热阻平均值求单元体等效导热系数比仅采用2种模型中的一种求单元体等效导热系数更精确.
4 实验论证
将实验值与λe-bc,λe-cb,λe进行对比,见表4.

表4 导热系数实验值与理论计算值比较Tab.4 Comparison between experimental values of thermal conductivity of hollow beads insulating mortar and theoretical formula values
横向热阻无穷小模型的计算值(λe-bc)比实验值略高,两者的平均偏差约为14%,横向热阻无穷大模型的计算值(λe-cb)则比实验值偏小,两者的平均偏差为11%,但是λe与实验值的平均偏差比二者的平均偏差均小,仅为0.2%.这也再次说明了本文提出的用2种模型等效热阻平均值来求单元体等效导热系数具有更高的精确度,同时也说明本文提出的基于最小热阻法则的理论计算方法用来快速估算玻化微珠保温砂浆导热系数是可行的.
5 结 论
1)基于最小热阻力法则和均匀化方法建立的2种模型的玻化微珠保温砂浆复合体系的等效导热系数计算值随玻化微珠粒子掺量的增加而逐渐降低.
2)单元体热阻网络的划分方式对等效导热系数的计算值有很大的影响.横向热阻无穷小模型的计算值均高于横向热阻无穷大模型的计算值,且随着玻化微珠掺量的增加这种趋势越来越明显.
3)从二维单元的温度云图可以看出,温度的梯度不是呈现完全的线性变化.热流矢量图则反映出大部分热流在遇到分散相时热流方向不再是沿着轴线方向,而是发生了偏转.
4)用横向热阻无穷大模型的等效热阻和横向热阻无穷小模型的等效热阻的算术平均值作为单元体的等效热阻求单元体等效导热系数比选择两种模型中的任意一种具有更高的精度.
5)对于玻化微珠保温砂浆,用基于最小热阻力法则和均匀化方法建立理论公式来估算玻化微珠保温砂浆的导热系数是可行的.
[1] 吴彻平,彭家惠,瞿金东,等.新型脱硫石膏基保温砂浆的配制及性能研究[J].材料导报,2011,25(10):121-124.
WU Che-ping,PENG Jia-hui,QU Jing-dong,et al.Investigation on preparation and properties of a novel gypsum-based thermal insulation mortar[J].Materials Review,2011,25(10):121-124.(In Chinese)
[2] 李珠,李赞婷.玻化微珠保温砂浆配合比研究及机理分析[J].新型建筑材料,2011,38(2):46-48.
LI Zhu,LI Zan-ting.Experiment on mix proportion of glazed hollow beads insulating mortar and its mechanism analysis[J].New Building Materials,2011,38(2):46-48.(In Chinese)
[3] 魏艳萍.玻化微珠保温混凝土抗压强度与导热系数研究[J].太原科技大学学报,2010,31(4):305-308.
WEI Yan-ping.The compressive strength and thermal conductivity research of vitrified microsphere thermal insulation concrete[J].Journal of Taiyuan University of Science and Technology,2010,31(4):305-308.(In Chinese)
[4] 李聚刚.玻化微珠酚醛树脂粉末复合保温浆料的研制[J].化学建材,2013(3):22-25.
LI Ju-gang.The development of phenolic resin powder and vitrified microsphere composite thermal insulating mortar[J].Chemical Materials for Construction,2013(3):22-25.(In Chinese)
[5] 张泽平,樊亚男,吴迪.掺加陶粒的玻化微珠保温混凝土试验研究[J].新型建筑材料,2011,38(11):21-24.
ZHANG Ze-ping,FAN Ya-nan,WU Di.Study on the experiment of thermal insulation glazed hollow bead concrete mixing with haycite[J].New Building Materials,2011,38(11):21-24.(In Chinese)
[6] 杨卓强,李珠,赵林,等.玻化微珠保温砂浆发泡技术及其机械喷涂的应用[J].施工技术,2011,40(6):23-25.
YANG Zhuo-qiang,LI Zhu,ZHAO Lin,et al.Foaming technology of vitrified microsphere insulation mortar and its application for mechanical spraying[J].Construction Technology,2011,40(6):23-25.(In Chinese)
[7] EUCKEN A.Thermal conductivity of ceramic refractory materials:calculation from thermal conductivity of constituents[J].Ceramic Abstract,1932(11):576;1933(12):231.
[8] 王家俊.聚酰亚胺/氮化铝复合材料的制备与性能研究[D].杭州:浙江大学高分子科学与工程系,2001.
WANG Jia-jun.Preparation and investigation on the polyimide/AIN composite materials[D].Hangzhou:Department of Polymer Science and Engineering,Zhejiang University,2001.(In Chinese)
[9] BRUGGEMAN D A G.Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen.I.Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen[J].Annalen der Physik,1935,416(7):665-679.
[10]FRICKE H.A mathematical treatment of the electric conductivity and capacity of disperse systems[J].Physical Review,1924(24):575-587.
[11]HAMILTON R L,CROSSER O K.Thermal conductivity of heterogeneous two-component systems[J].Industrial & Engineering Chemistry Fundamental,1962,1(3):187-191.
[12]HASSELMAN D P H.Effective thermal conductivity of composites with interfacial thermal barrier resistance[J].Journal of Composite Materials,1987,21(6):508-515.
[13]JAMES B W,WOSTERTHOLM G H,KEEN G S,et al.Prediction and measurement of the thermal conductivity of composite materials[J].Physics,1987,20:261-268.
[14]RAMANI K ,VAIDYANATHAN A.Finite element analysis of effective thermal conductivity of filled polymeric composites[J].Composite Materials,1995,29:1725-1740.
[15]尧璟云,阮丰乐,程颐.无机玻化微珠保温砂浆的质量控制[J].新型建筑材料,2011,38(12):5-7.
YAO Jing-yun,RUAN Feng-le,CHENG Yi.Quality control of glazed hollow bead inorganic insulation mortar[J].New Building Materials,2011,38(12):5-7.(In Chinese)
[16]张建隽,李建宇.玻化微珠保温混凝土抗压强度与导热系数试验研究[J].混凝土与水泥制品,2012(3):60-62.
ZHANG Jian-jun,LI Jian-yu.Experimental research on compressive strength and thermal conductivity of thermal insulation glazed hollow bead concrete[J].China Concrete and Cement Products,2012(3):60-62.(In Chinese)
[17]HARMATHY T Z.Thermal properties of concrete at elevated temperatures[J].Journal of Materials,1970,5:47-74.
[18]KONG M,ZHAO W J,WEI L,et al.Investigations on the microstructure and hardening mechanism of TiN/SiN nano composite coatings[J].J Phys D:Appl Phys,2007,40(9):2858.
[19]奚同庚.无机材料热物性学[M].上海:上海科学技术出版社,1981:69-75.
XI Tong-geng.Thermophysical properties of inorganic[M].Shanghai:Shanghai Science and Technology Publishing House,1981:69-75.(In Chinese)
[20]陈则韶,钱军,叶一火.复合材料等效导热系数的理论推算[J].中国科学技术大学学报,1992,22(4):416-423.
CHEN Ze-shao,QIAN Jun,YE Yi-huo.The theoretical calculation of effective thermal conductivity of composite materials[J].Journal of University of Science and Technology of China,1992,22(4):416-423.(In Chinese)
Study on the Thermal Conductivity Model of Hollow Beads Insulating Mortar
GONG Jian-qing†,ZHANG Chan-tao
(College of Civil Engineering,Hunan Univ,Changsha,Hunan 410082,China)
Based on the minimum thermal resistance theory and homogenization method,the effective thermal conductivity of hollow beads insulating mortar was estimated.With ANSYS imitating the heat transmission of the 2Dunit model of hollow beads insulating mortar,we can find it will bring about calculation errors by considering the extreme cases of the transverse thermal resistance of resistance network.Compared with the effective thermal conductivity of 3Dunit cell model calculated by ANSYS with three kinds of theoretical calculating value,it is more accurate than the effective thermal conductivity of unit calculated by the model of effective thermal resistance average.A model was built by assuming transverse thermal resistance infinitesimal and infinite.Final laboratory finding also confirms this conclusion.With only 0.2%deviation between the experiment values and the calculation of theoretical model,it is feasible to estimate the effective thermal conductivity of hollow bead insulating mortar.
minimum thermal resistance;homogenization method;effective thermal conductivity;hollow beads insulating mortar;finite element simulation
TU502
A
1674-2974(2014)06-0099-07
2014-02-12
国家自然科学基金资助项目(51278180)
龚建清(1963-),男,湖南湘乡人,湖南大学副教授,硕士生导师,博士
†通讯联系人,E-mail:gongjianqing123@yahoo.com.cn

