复杂高层结构随机地震反应中阻尼模型的影响分析＊

杨永胜，陈清军†

（1.同济大学 土木工程防灾国家重点实验室，上海 200092；2.同济大学 结构工程与防灾研究所，上海 200092）

复杂高层结构随机地震反应中阻尼模型的影响分析＊

杨永胜1，2，陈清军1，2†

（1.同济大学 土木工程防灾国家重点实验室，上海 200092；2.同济大学 结构工程与防灾研究所，上海 200092）

扼要比较了Rayleigh阻尼和Caughey阻尼两种阻尼模型，利用ANSYS软件中的APDL编程语言进行二次开发，将Caughey阻尼模型应用到复杂高层建筑结构的随机地震反应分析中；以某实际复杂高层建筑为例，采用现场测试和数值模拟相结合的方法，分析了不同阻尼模型对复杂高层结构随机地震反应计算结果的影响，讨论了Rayleigh阻尼模型和Caughey阻尼模型的适用范围.结果表明，Rayleigh阻尼模型的曲线形状与所选取的控制频率相关，两控制频率间的计算阻尼比小于实测结果，两控制频率以外部分的计算阻尼比则大于实测阻尼比；Caughey阻尼模型能在较大频率范围内较准确地反映结构的阻尼特性.

阻尼；抗震设计；随机地震反应；ANSYS二次开发；振动测试

近年来，国内外相继兴建了许多复杂高层及超高层建筑，这些特殊的高层及超高层建筑结构的组成成分、耗能机理和振动特性都比较复杂，其阻尼矩阵的形成也有其特殊性［1］.目前，在高层建筑地震反应分析中往往采用Rayleigh阻尼模型来构建阻尼矩阵，对于一般结构，往往选取结构的第1和第2阶振型参数来形成Rayleigh阻尼矩阵.但对于复杂高层及超高层结构而言，高阶振型对结构地震反应的影响将不容忽视，而且对于复杂高层结构的某些构件，在地震反应分析中起控制作用的可能不再是低阶振型，因此如果采用只考虑2个低阶振型的Rayleigh阻尼模型，将会导致结构的地震反应分析结果产生较大的偏差［2］.

本文将首先扼要比较Rayleigh阻尼和Caughey阻尼2种阻尼模型，利用ANSYS软件中的APDL编程语言进行二次开发，以将Caughey阻尼模型应用到复杂高层建筑结构的随机地震反应分析中，并以某实际复杂高层建筑为例，采用现场测试和数值模拟相结合的方法，分析不同阻尼模型对复杂高层结构随机地震反应计算结果的影响.

1 两种阻尼模型比较

在结构动力分析中，一般假定阻尼力的大小与质点振动的速度成正比，即采用黏滞阻尼模型［3－4］.为了应用振型叠加法，一般假定振型关于阻尼矩阵C正交.目前，多自由度体系的阻尼矩阵主要有Rayleigh阻尼和Caughey阻尼2种模型.

Rayleigh阻尼模型作为目前应用最为广泛的阻尼模型，该模型假定结构的阻尼矩阵是质量矩阵和刚度矩阵的线性组合，通常称为比例阻尼：

式中：ωm，ωn，ξm，ξn分别为体系第m和n阶振型的自振频率及对应的振型阻尼比.振型阻尼比是结构体系耗能特性的宏观描述，易于从实验和实测试验中获取.当各阶阻尼比相同时，即ξm＝ξn＝ξ，式（2）可简化为：

对于一般工程结构而言，因为低阶振型在结构的动力反应中起主导作用，通常取低阶振型来确定比例系数a0和a1，其他各阶振型的阻尼比可通过式（4）求解：

式中：ωj为第j阶的自振频率；ξj为相应于第j阶的阻尼比.

Caughey阻尼又称扩展的Rayleigh阻尼.若要求更多阶振型的阻尼比满足实测阻尼比，则必须构造更多项的线性组合，Caughey阻尼能较好地满足这个要求.Caughey阻尼可写成如下形式［3］：

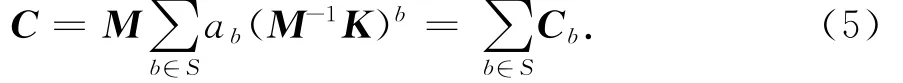
式中：ab是Caughey阻尼模型中的比例系数，集合S包含n个任意整数值，n的大小和S的具体元素取决于阻尼比曲线拟合结果.根据黏滞阻尼假定，推导得出项b对于广义阻尼值的贡献为：

上式提供了根据指定振型数目、自振频率和阻尼比计算系数ab的途径：将已知的n个自振频率以及实测的n阶阻尼比代入该式，得到n阶线性代数方程组，从中可以解得n个待定常数ab值；然后按式（5）形成阻尼矩阵，这样使得参与计算的n阶振型的阻尼比与实际量测结果吻合.理论上S可包含－∞到＋∞之间的任意整数值，但实践上，S中元素值选择越接近于零越好，这样有助于保证数值计算的稳定，当S＝｛0，l｝时，即为式（1）所示的 Rayleigh阻尼模型.本文利用ANSYS软件中的APDL编程语言进行二次开发，从而借助ANSYS软件将Caughey阻尼模型应用到复杂高层建筑结构的随机地震反应分析中.

同时，利用振型关于阻尼矩阵正交的假定，亦可推导得出第n阶振型的广义阻尼为：

2 某高层建筑结构动力特性测试

本文采用同济大学某复杂高层建筑为例，进行阻尼模型对复杂高层结构随机地震反应结果的影响分析.该建筑上部结构为21层巨型钢框架结构体系.框架的层高为4m，每边9跨，跨度为5.4m，结构平面尺寸为48.6m×48.6m，主体结构采用钢框架加外围支撑的形式.主楼楼层中部楼板缺失，形成L型3平面，往上顺时针旋转，每3层旋转90°，到顶层共旋转6次.该建筑较多楼层的楼板开洞面积大于楼板面积的35%，有效楼板宽小于典型楼板宽度的40%；结构沿高度每隔3层设2m高设备层，竖向刚度突变，该建筑属于典型的平面不规则和竖向刚度不规则的复杂高层结构.柱子采用钢管混凝土柱，截面尺寸900mm×900mm，梁采用 H型钢（700mm×300mm×24mm×13mm）（高度×宽度×腹板厚度×翼缘厚度），弦杆采用H型钢（500 mm×200mm×16mm×10mm）（高度×宽度×腹板厚度×翼缘厚度），腹杆采用H型钢（200mm×200mm×12mm×8mm）（高度×宽度×腹板厚度×翼缘厚度），支撑圆管（φ300mm×16mm），表1为结构主要构件的材料参数.

表1 结构部件材料参数Tab.1 Material parameters of structural parts

目前结构自振特性主要测试方法有稳态正弦激振法、传递函数法、自由振动法和脉动测试法.其中脉动测试法是利用环境随机振动作为结构物激振的振源来测定并分析结构物固有特性，是近年来随着计算机技术及FFT理论的普及而发展起来的，现已被广泛应用于建筑物的动力分析研究中.本文采用脉动测试法对该复杂高层结构进行了动力特性测试，所用仪器为美国凯尼公司生产的Basalt型数字振动测试仪.为了排除高频背景噪声的干扰，使得测试结果的低频成分更真实，本次测试将仪器采样频率调整到50Hz.地脉动激励可以看作为各态历经的平稳随机过程，只要测试时间足够长，可以用单个样本函数上的时间平均来描述这个过程的所有样本的平均特性.本次测试记录时间设定为20min以上，本次测试的测点选择在该高层结构21层楼梯间拐角处，其中某测试样本的时程如图1所示.

图1 测试得到的某样本时程Fig.1 A time history sample of the field test results

脉动激励的频谱通常情况下是比较平坦的，可以看成是有限带宽的白噪声，建筑结构振动信号的功率谱在自振频率处会出现较大的峰值.将测试所得的信号求其自功率谱，通过峰值所在频率点来识别结构的自振频率.对各阶自振频率对应的阻尼比，可采用半功率法求取，由半功率点幅值H（ω）／确定半功率带宽Δω，然后根据式（10）计算：

式中：ωk为第k阶自振频率；H（ωk）为k阶自振频率处的峰值.图1所示测试样本的功率谱曲线见图2，表2给出了本次测试的结构自振频率和阻尼比.

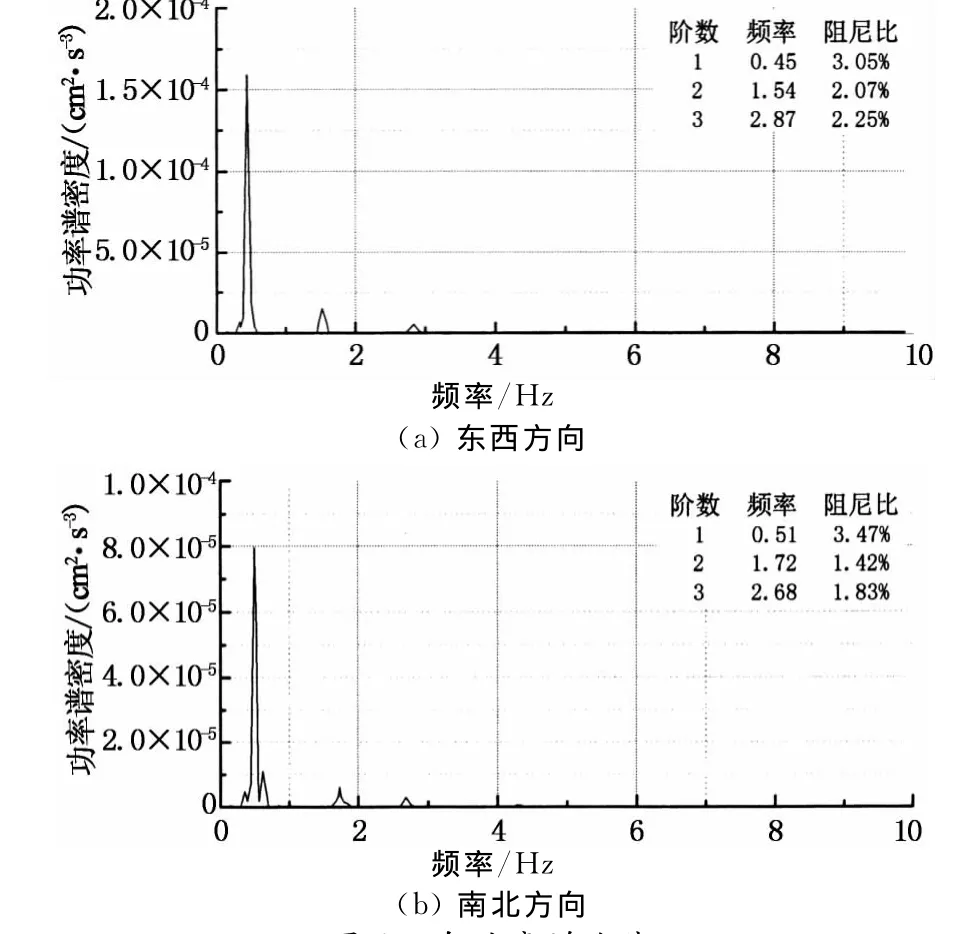
图2 自功率谱曲线Fig.2 Auto-power spectrum curves

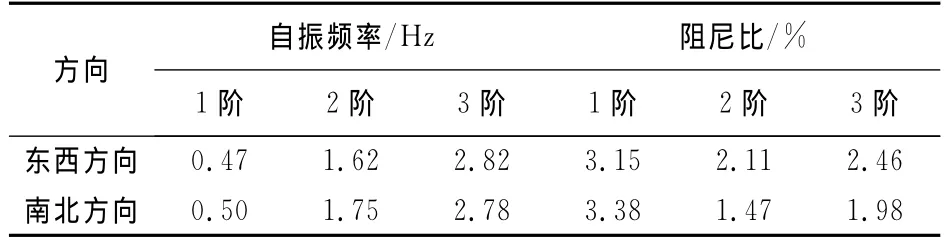
表2 结构自振频率和阻尼比的测试结果Tab.2 Natural frequency and damping ratio of the field test

3 某复杂高层结构有限元模型及随机地震动输入

3.1 结构有限元模型的建立

为进行复杂高层结构的随机地震反应分析，采用ANSYS软件建立三维有限元模型［5］，其中梁、柱、斜撑和腹杆采用Beam188单元来模拟，楼板用Shell63单元来模拟，建立的某复杂高层建筑结构三维有限元模型如图3所示.

由于地脉动激励强度较弱，一般低阶自振频率和对应的阻尼比精度较高，与实际比较相符.本文采用东西方向和南北方向第一阶自振频率对应阻尼比的平均值作为该复杂高层结构的参考阻尼比，具体取值为3.3%.

数值模型的自振特性见表3，将前三阶自振频率与实测结果比较，第一阶的相对误差为2%，第二阶的相对误差为5.2%，第三阶的相对误差为7.4%，表明本次有限元模型具有较高精度.表中同时也给出了振型对应的振型参与系数和累积有效质量参与系数.复杂高层结构进行抗震设计时，要求各振型累积参与质量之和不低于90%［6－7］，为了更精确地比较2种阻尼模型下复杂高层结构地震反应的不同以及考虑到高阶振型对复杂高层结构地震反应的影响，本文取前150阶振型参与计算，输入激励的频率取0～20Hz.

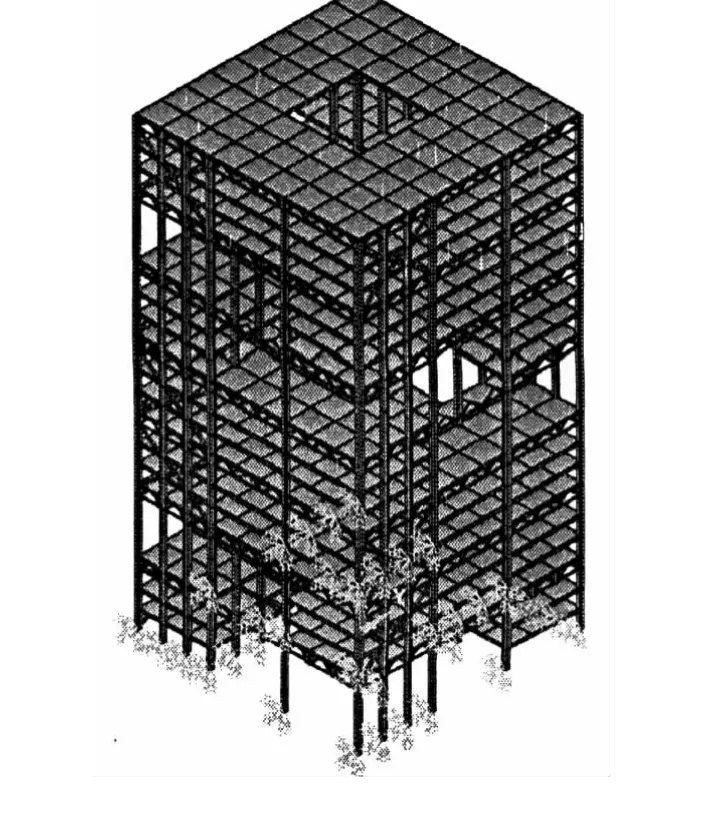
图3 结构三维有限元模型Fig.3 The three dimension finite element model

表3 结构自振特性表Tab.3 Natural vibration characteristics of the finite element model

3.2 随机地震动输入模型

本文采用杜修力于1998年提出的修正地表随机地震动模型作为输入激励，其功率谱密度表达式为：［8］

式中：ωg和ξg分别为场地土的卓越频率和阻尼比；ω0≈1.83为低频拐角频率；D＝1／28π为与震源有关的参数.杜修力修正模型假定基岩地震动为有色谱，在大量实际地震记录的统计基础上，加入高通滤波器ω4／ （ω2＋）2和低通滤波器1／［1＋（Dω）2］，合理修正了高频能量和低频能量，与实际地震动特征比较相符.

4 两种不同阻尼模型下的计算结果分析

4.1 Raleigh阻尼模型下的计算结果分析

首先，取结构实测的参考阻尼比3.3%作为各阶振型阻尼比，根据振型叠加原理，利用随机振动CQC（complete quadratic combination）法进行计算，其计算结果作为参考真实解.选取5组Rayleigh阻尼模型进行计算，第一组取结构1阶、4阶自振频率作为控制频率，记作R1；第二组取结构1阶、10阶自振频率作为控制频率，记作R2；第三组取结构1阶、25阶自振频率作为控制频率，记作R3；第四组取结构1阶、40阶自振频率作为控制频率，记作R4；最后一组取结构的1阶、150阶自振频率作为控制频率，记作R5.各组阻尼模型的拟合曲线见图4，从图中可看出，阻尼曲线的形状主要与控制频率点及两控制频率之间的间距有关：两控制频率之间的部分计算阻尼小于实际的结构阻尼，两控制频率以外的部分计算阻尼则大于实际的结构阻尼.所以，控制频率的合理选取是计算结果准确与否的关键.

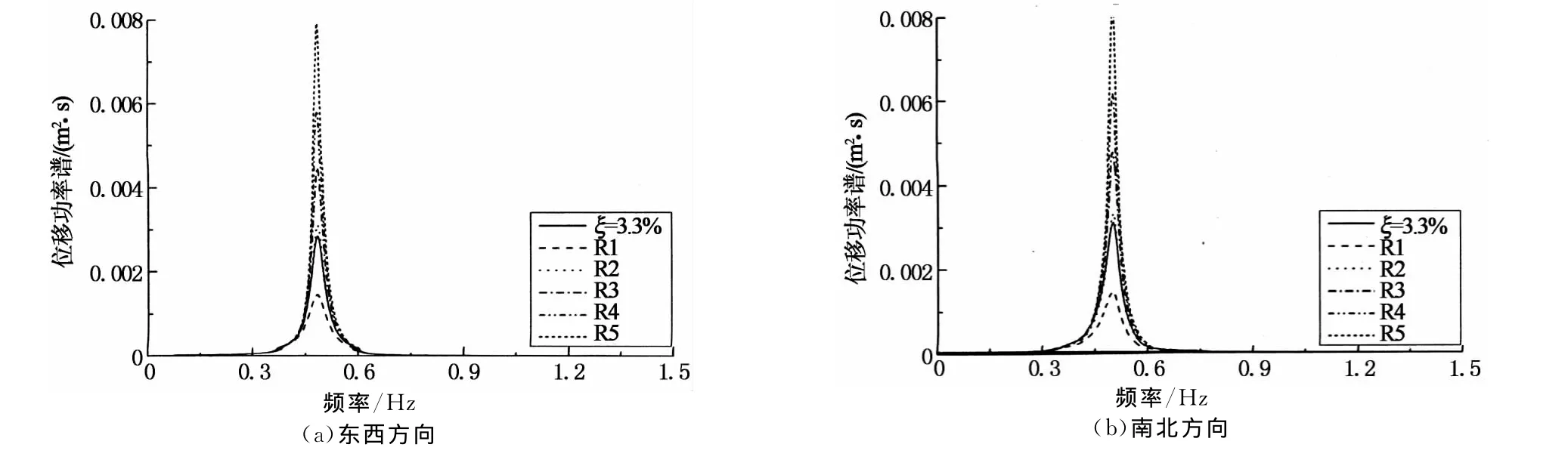
图5 顶层位移功率谱密度Fig.5 Displacement power spectral density of roof response

分别计算各Raleigh阻尼模型工况下结构的随机振动响应，选取结构顶层节点作为参考点，图5为结构顶层的位移功率谱计算结果；分别在每层楼板处选取一个参考点，计算其随机振动响应，然后根据随机振动理论，通过计算各响应量的各阶谱矩，来估算响应最大值的均值，图6为楼层的位移极值包络图.

图4 不同控制频率下的Rayleigh阻尼模型Fig.4 Rayleigh damping model under different control frequencies

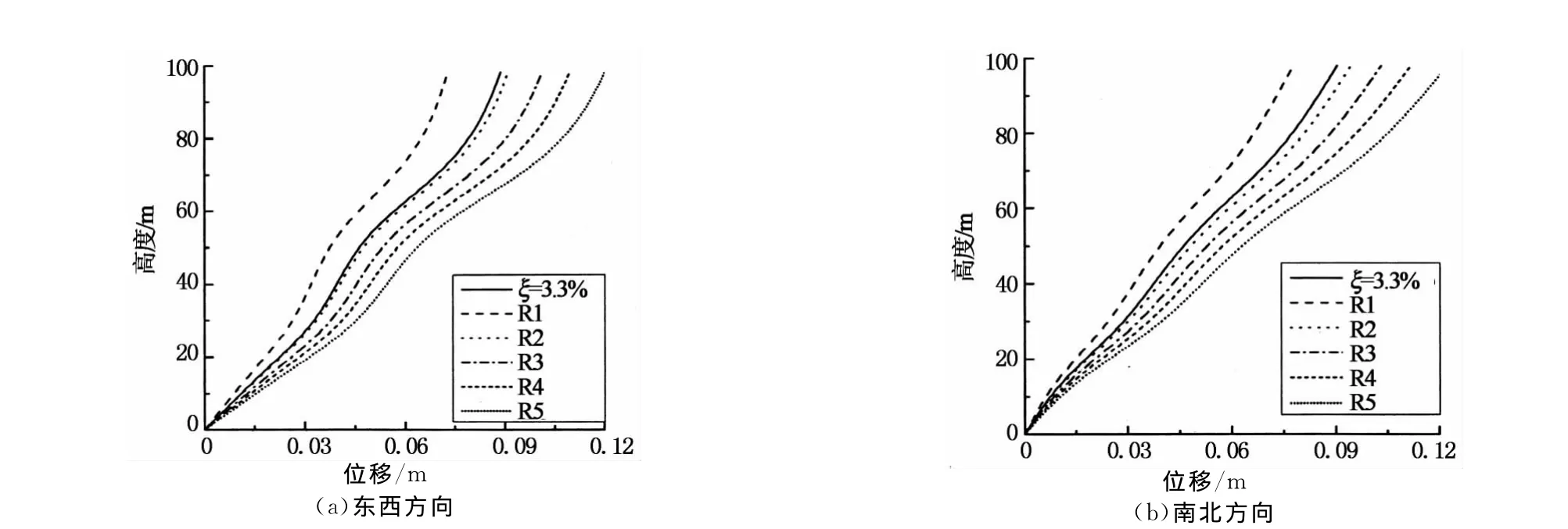
图6 楼层位移极值包络图Fig.6 Maximum relative displacement response along structural height

从图5和图6可看出由结构1阶、5阶自振频率为阻尼控制频率（R2）的计算结果与真实解最为接近，由结构前两阶自振频率为阻尼控制频率（R1）的计算结果明显偏小，说明其计算阻尼偏大，低估了结构的响应.其余3种情况（R3，R4，R5）的计算结果比真实值偏大，说明其计算阻尼比实际阻尼要小.

4.2 Caughey阻尼模型下的计算结果分析

由式（9）可知，当i＝2时，Caughey阻尼模型将与Raleigh阻尼模型相同，本文分别选取i＝5，7，9三种情况确定的Caughey阻尼模型进行计算.i＝5时，分别选取结构的第1，5，10，15，25阶自振频率作为控制频率；i＝7时，分别选取结构的第1，5，10，15，25，40，60阶自振频率作为控制频率；i＝9时，分别选取结构的第1，5，10，15，25，40，60，100，150阶自振频率作为控制频率；各组阻尼模型的拟合曲线见图7.

图7 不同控制频率下的Caughey阻尼模型Fig.7 Caughey damping model under different control frequencies

图8为各组Caughey阻尼模型下结构顶层的位移功率谱计算结果，图9为楼层位移极值包络图.从图中可以看出9个基本频率点控制的Caughey阻尼模型计算结果与参考真实值最为接近，随着控制频率点数的增加，计算结果越来越靠近真实值.由此可见，控制频率点的数目及控制频率选取的合理性是决定Caughey阻尼模型精确与否的关键.

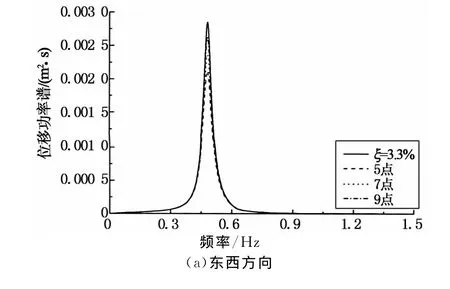
图8 顶层位移功率谱密度Fig.8 Displacement power spectral density of roof response

图9 楼层位移极值包络图Fig.9 Maximum relative displacement response along structural height

对比图5，图6与图8，图9可知，采用Caughey阻尼模型的计算结果比采用Reyleigh阻尼模型的计算结果更接近真实解，Caughey阻尼在广义上可以看作是对已知的阻尼比－频率数据以幂函数为底的非线性拟合，能在较大频域范围内更准确地反映结构的阻尼特性.在进行随机地震反应分析时，采用Caughey阻尼的计算结果更能反映实际情况.

5 结 语

本文以某实际复杂高层建筑为例，采用现场测试和数值模拟相结合的方法，分析了不同阻尼模型对复杂高层结构随机地震反应计算结果的影响，讨论了Rayleigh阻尼模型和Caughey阻尼模型的适用范围.本文的分析表明：

1）Rayleigh阻尼模型的曲线形状与所选取的控制频率相关，两控制频率间的计算阻尼比小于实测结果，两控制频率以外部分的计算阻尼比则大于实测阻尼比；对于高阶振型对地震反应贡献较大的复杂高层建筑而言，选取前两阶振型作为Rayleigh阻尼的控制频率会产生较大误差.

2）Caughey阻尼模型在广义上可以看作是对已知的阻尼比－频率数据以幂函数为底的非线性拟合，能在较大频域范围内更准确地反映结构的阻尼特性.对于高阶振型对地震反应贡献较大的复杂高层建筑而言，在结构随机地震反应分析中，采用Caughey阻尼模型可获得更高精度的计算结果.

3）本文分析的2种阻尼模型（Rayleigh阻尼模型和Caughey阻尼模型）属于比例阻尼范畴.对于多于1种材料组成的结构，由于不同材料在结构的不同部分提供的能量损失机制差别较大，将导致阻尼不是成比例的；对此，可将每一个明显的结构组成部分都建立一个比例阻尼矩阵，然后将其直接集装形成组合的体系矩阵加以处理.对于更一般的广义比例阻尼及非比例阻尼问题则需要进一步研究.

［1］ 段绍伟，向湘林，沈蒲生.复杂阻尼结构阻尼模型研究［J］.振动与冲击，2011，30（2）：73－76.

DUAN Shao-wei，XIANG Xiang-lin，SHEN Pu-sheng.Damping model of a complex structure［J］.Journal of Vibration and Shock，2011，30（2）：73－76.（In Chinese）

［2］ 沈飞，楼梦麟.超高层建筑地震反应中高阶振型影响分析［J］.工程力学，2012，29（SⅠ）：23－28.

SHEN Fei，LOU Meng-lin.Influence of high modes of super high-rise building on its seismic responses［J］.Engineering Mechanics，2012，29（S I）：23－28.（In Chinese）

［3］ CLOUGH R W，PENZIEN J.Dynamics of structures［M］.New York：McGraw-Hill，1993：183－193.

［4］ CHOPRA A K.Matrix dynamics of structures：theory and applications to earthquake engineering［M］.2nd ed.New Jersey：Prentice-Hall，2001：454－462.

［5］ 王新敏.ANSYS工程结构数值分析［M］.北京：人民交通出版社，2007：542－553.

WANG Xin-min.ANSYS numerical analysis of engineering structure［M］.Beijing：China Communications Press，2007：542－553.（In Chinese）

［6］ GB 50011—2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010：320－325.

GB 50011—2010Code for seismic design of buildings［S］.Beijing：China Architecture ＆ Building Press，2010：320－325.（In Chinese）

［7］ WILSON E L.Three-dimensional static and dynamic analysis of structures［M］.Berkeley，California：Computers and Structures，Inc，2002：12－13.

［8］ 杜修力.水工建筑物抗震可靠度设计和分析用的随机地震输入模型［J］.地震工程与工程振动，1998，18（14）：76－81.

DU Xiu-li.A random seismic input model used in seismic reliability design and analysis of hydraulic buildings［J］.Earthquake Engineering and Engineering Vibration，1998，18（14）：76－81.（In Chinese）

Influence of the Damping Model of Complex High-rise Building Structure on Its Random Seismic Response

YANG Yong-sheng1，2，CHEN Qing－jun1，2†
（1.State Key Laboratory of Disaster Reduction in Civil Engineering，Tongji Univ，Shanghai 200092，China；2.Research Institute of Structural Engineering and Disaster Reduction，Tongji Univ，Shanghai 200092，China）

A comparative analysis between Rayleigh damping model and Caughey damping model was first conducted，and then，by ANSYS secondary developing based on APDL programming language，the Caughey damping model was successfully applied to the random seismic response analysis of complex highrise building structure.An actual complex high-rise building structure was selected as the research object.By using the combination method of field vibration test and numerical simulation，the influence of different damping models on the random seismic response of complex high-rise building was analyzed，and the applicability and effectiveness of the two damping models were also discussed.The results have indicated that the curve shape of Rayleigh damping model is closely related to the control frequencies，the calculated damping ratio is lower than the actual test damping ratio between two control frequencies，and it is contrary among other frequency ranges.The Caughey damping model can more accurately meet the actual damping in a wider frequency range.

damping；seismic design；random seismic response；ANSYS secondary development；vi-bration test

TU311.3

A

1674-2974（2014）06-0028-07

2013-08-22

国家自然科学基金资助项目（50978198）

杨永胜（1984－），男，山西忻州人，同济大学博士研究生

†通讯联系人，E-mail：chengj＠tongji.edu.cn