考虑瞬态热应变的钢筋混凝土板火灾反应分析＊

王 勇，董毓利，袁广林，王 耀

（1.江苏省土木工程环境灾变与结构可靠性重点试验室（中国矿业大学），江苏 徐州 221008；2.深部岩土力学与地下工程国家重点试验室（中国矿业大学），江苏 徐州 221008；3.华侨大学 土木工程学院，福建 厦门 361000；4.北京工业大学 建筑工程学院，北京 100124）

考虑瞬态热应变的钢筋混凝土板火灾反应分析＊

王 勇1，2†，董毓利3，袁广林1，王 耀4

（1.江苏省土木工程环境灾变与结构可靠性重点试验室（中国矿业大学），江苏 徐州 221008；2.深部岩土力学与地下工程国家重点试验室（中国矿业大学），江苏 徐州 221008；
3.华侨大学 土木工程学院，福建 厦门 361000；4.北京工业大学 建筑工程学院，北京 100124）

基于非线性温度场理论，编制了钢筋混凝土构件的温度场分析程序；通过对不同温度-应力途径试件力学行为的对比分析，说明了瞬态热应变的重要性，并提出双轴受压状态下瞬态热应变计算模型和瞬态模量的概念；根据大挠度板单元和热弹塑性本构模型，建立了钢筋混凝土双向板的有限元计算模型，对3块钢筋混凝土双向板的火灾行为进行数值模拟，分析了瞬态热应变和膨胀应变对其火灾行为的影响.计算结果表明，计算模型结果与试验结果吻合较好，验证了瞬态热应变模型的有效性，参数分析得出膨胀应变和瞬态热应变对钢筋混凝土双向板的火灾行为有重要影响.

钢筋混凝土板；火灾；瞬态热应变；瞬态模量；膨胀应变

在火灾作用下，结构中楼板因大变形而引起的薄膜效应对防止结构倒塌破坏起着重要的作用.为了研究楼板的受拉薄膜效应，国内外学者进行了较多的钢筋混凝土板抗火试验［1－4］.

由于试验费用昂贵、周期长等原因，近年来，数值模拟成为对楼板抗火性能进行深入研究的一种较为经济、有效的方法.一般地，通过考虑温度对力学参数的影响，将常温本构模型推广到高温状态，发展相应的高温本构模型，用于模拟钢筋混凝土板的火灾行为.研究表明［4－6］，热弹塑性本构模型应用较为广泛.

目前，由于缺乏试验数据，还没有公认的双轴受压瞬态热应变模型，其对钢筋混凝土板火灾行为的影响研究也相对较少.鉴于此，本文在单轴瞬态热应变模型的基础上，提出双轴受压状态下瞬态热应变模型以及瞬态模量的概念，通过对3块钢筋混凝土双向板的火灾行为进行数值模拟，验证了该模型.在此基础上，研究了瞬态热应变和膨胀应变对钢筋混凝土双向板火灾行为的影响.

1 本构模型

1.1 混凝土

如图1所示，采用常温下广泛使用的Hinton弹塑性模型，混凝土屈服函数F（T）表达式为：

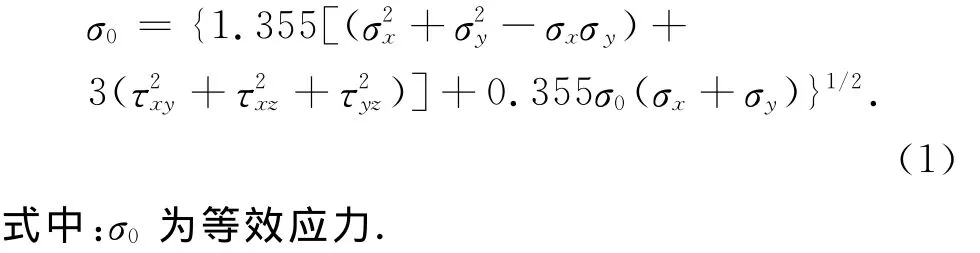
图1 高温下混凝土屈服面Fig.1 Yield surface of concrete at elevated temperatures

如图2所示，采用文献［7］的混凝土单轴应力－应变关系模型.

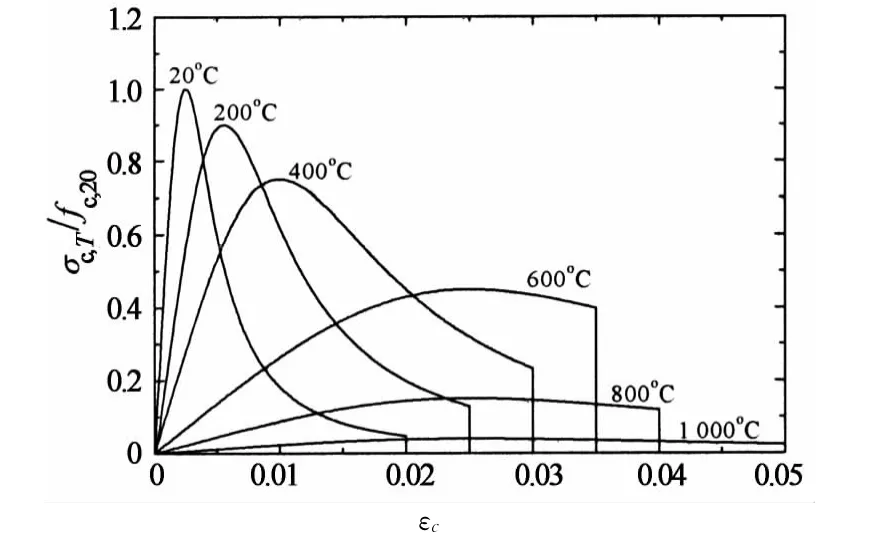
图2 高温混凝土应力-应变关系Fig.2 Stress-strain relationship of concrete at elevated temperatures

根据单轴应力－应变关系，可得等效应力和等效塑性应变的计算模型［3］，即：

对于单轴瞬态热应变计算模型，目前通常采用Anderberg模型［11］，即：

图3 钢筋应力-应变关系Fig.3 Stress-strain relationship of steel

图4 钢筋应变硬化模型Fig.4 Strain-hardening model of steel

式中：εcu，T取文献［7］中的温度T时峰值应变.

1.2 钢筋

如图3所示，采用文献［7］提出的钢筋应力-应变模型.

如图4所示，钢筋采用等向应变硬化模型，具体表达式为：

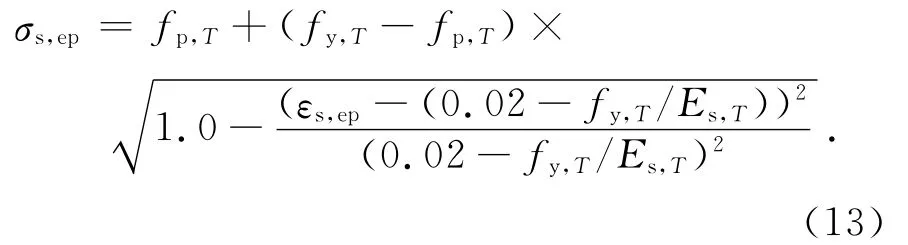
式中：fp，T为比例极限；fy，T为屈服强度；Es，T为弹性模量；σs，ep为等效塑性应力；εs，ep为等效塑性应变.

钢筋膨胀应变模型采用以下两式计算.

钢筋应力（psi），t是时间（h）.

钢筋极限应变采用下式计算［8］，即：

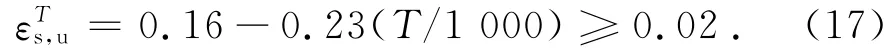
2 求解非线性方程

在修正牛顿拉夫逊增量迭代中，采用位移收敛准则来控制迭代过程，收敛容差取10－4.同时，规定最大迭代次数为20.

值得指出的是，在构件火灾行为分析的后期，需采用弧长法计算，即外荷载不再保持常值.当刚度矩阵奇异时，认为板达到破坏状态，相应时刻即为耐火极限.

3 瞬态热应变模型

为验证瞬态热应变的重要性，选取2个典型算例进行分析，其中混凝土膨胀应变模型采用式（7）.

3.1 过镇海试验

过镇海等进行了两端约束的混凝土棱柱体加热试验［8］，试件常温抗压强度为23.4MPa.模型计算结果和试验结果对比如图5（a）所示.

图5 瞬态热应变模型验证Fig.5 Validation of the transient strain model

计算表明，当考虑瞬态热应变时，理论曲线与试验曲线变化规律比较一致，符合高温下混凝土的受热性能机理.当温度小于200℃时，以自由膨胀变形为主，瞬态热应变较小，为保持试件总变形为零，自由膨胀变形主要由受力引起的应变相抵消.由于试件温度较低，混凝土弹性模量相对较大，受力引起的应变增加导致压应力的迅速增长；随着压应力的增大，瞬态热应变分量迅速发展；此时，瞬态热应变的缩短与膨胀应变值相近，故应力变化幅度变小.当温度较高时，自由膨胀变形增长趋缓，而瞬态热应变急剧发展，为维持总应变分量为零，试件发生应力松弛.

当忽略瞬态热应变时，试件的应力几乎呈直线上升，应力未得到充分释放.在380℃时就达到相应的抗压强度而破坏，明显地从性质上与试验行为不符.

3.2 Anderberg试验

Anderberg等对2个圆柱体混凝土试件进行了试验［11］.第一、第二试件常温抗压强度分别为34.7 MPa和41.3MPa.

第一个试件首先升温至400℃，并保持温度，随后加载至0.45 fc，20；第二个试件是首先加载至0.45 fc，20，随后升温到400℃.试验结果和模型计算结果如图5（b）所示.同样，当不考虑混凝土的瞬态热应变时，计算结果与试验结果差别明显.

由此看来，瞬态热应变非常重要，在数值计算中必须认真考虑.

4 模型验证

本文选用文献［2］（编号4ES-2）和文献［3，15］（编号D147，661）的3块钢筋混凝土双向简支板来验证瞬态热应变模型.板的材性性能参数见表1.由于对称性，每块板取1／4进行计算.

4.1 温度场计算

在温度分析中，采用四节点矩形单元将板沿厚度划分为20层.热工性能参数参见文献［7］.

对于D147板，从受火面算起，热电偶分别布置在0mm，22mm，48mm，75mm和95mm位置.对于661板，文献［15］只给出了板底钢筋温度和非受火面的平均温度.对于4ES-2板，从受火面开始，热电偶布置位置分别为0mm，20mm，40mm，60 mm，80mm，100mm和120mm.三板温度场计算结果与实测结果对比如图6所示.由图可知，计算结果和试验结果吻合较好，计算温度场数据可用于双向板的火灾行为分析.

图6 温度场计算结果与试验结果对比图Fig.6 Comparison between measured and predicted temperatures

4.2 数值模拟

结合温度场分析结果，采用上述本构模型对3块钢筋混凝土双向简支板进行数值模拟.值得指出的是，本构模型及计算程序在常温下的有效性已经验证，具体参见文献［16］.

由图7可知，初始阶段，由于热膨胀应变作用和截面较大的温度梯度，致使板具有较高的变形速率；随着变形的增加，板中心区域的薄膜效应逐渐由压变为拉，即受拉薄膜效应逐渐发展，变形速率变缓；最后阶段，对于D147和661两板，随着混凝土达到压应变而破坏，钢筋力学性能严重退化，特别是钢筋徐变率较大，钢筋很快达到破坏应变，刚度矩阵奇异，致使板最终破坏.对于4ES-2板，不是钢筋达到极限应变，而是大量混凝土达到极限应变，导致刚度矩阵奇异，板最终破坏.

图7 3板中心挠度-时间计算曲线与试验曲线对比Fig.7 Comparison between measured and predicted deflection-time curves of three slabs

此外，与前2个板不同，4ES-2板在后期阶段表现出较好的变形性能.一方面，这是由于4ES-2板的钢筋类型为热轧变形钢筋，而其他2板的钢筋为冷拉变形钢筋；另一方面，如图6所示，与前2个板最后阶段钢筋温度相比（700℃），4ES-2板的钢筋温度相对较低（600℃）.由此看来，钢筋力学性能对结构后期火灾行为有重要影响.

5 参数分析

以上述钢筋混凝土双向板为分析对象，本文研究了瞬态热应变和膨胀应变对双向板火灾行为的影响.

5.1 瞬态热应变

由上可知，瞬态热应变对混凝土的力学行为有重要影响，即不考虑瞬态热应变，试件的应力较大，无法得到充分释放，使得试件较早地破坏，与实际的力学作用机理不符.

因此，本文研究了瞬态热应变对钢筋混凝土双向板火灾行为的影响.其中，混凝土和钢筋的膨胀应变模型均采用文献［7］模型.模型计算结果和试验结果对比如图8所示.

图8 瞬态热应变对3板中心挠度的影响Fig.8 Effect of transient strain on the mid-span deflections of three slabs

由图可知，前期阶段，瞬态热应变对钢筋混凝土的火灾行为影响较小，膨胀应变是主要因素.随后，瞬态热应变的影响越来越大.当不考虑瞬态应变时，钢筋混凝土板的变形较大，原因在于受压区混凝土的应力无法释放，混凝土塑性应变增大，同时也使得受拉区开裂较多，最终致使刚度矩阵奇异，板较早地破坏.

因此，瞬态热应变对钢筋混凝土双向板的中后期行为有较大影响，在数值分析中应该考虑.

图9 混凝土和钢筋的热膨胀模型Fig.9 Thermal strain models of concrete and steel

5.2 膨胀应变

膨胀应变是高温下材料的主要应变之一，本文研究了其对混凝土板火灾行为的影响规律.

如图9所示，分别采用Eurocode 2，Lie和Nechnech膨胀应变模型进行分析.不同膨胀应变模型的计算结果与试验结果对比如图10所示.

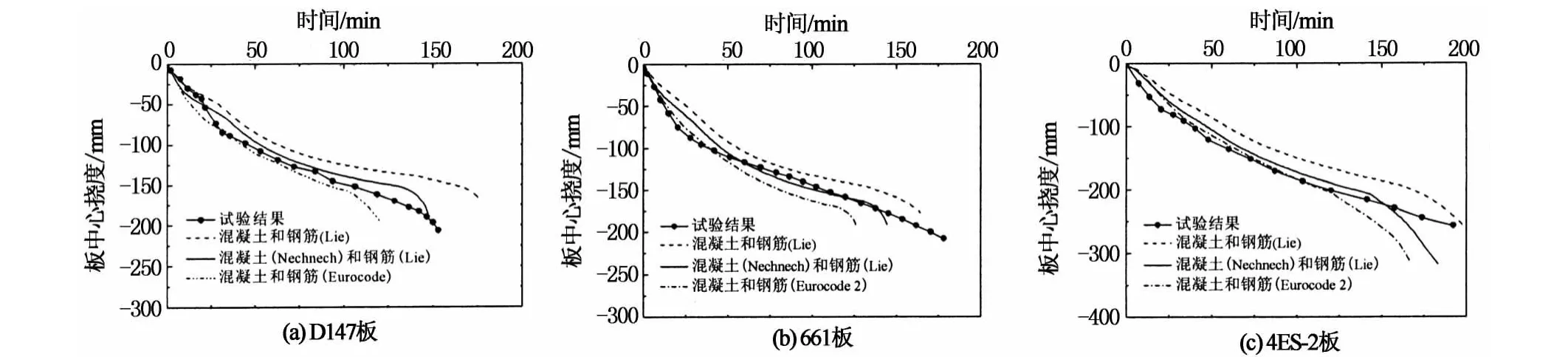
图10 膨胀应变对3板中心挠度的影响Fig.10 Effect of thermal strain on the mid-span deflections of three slabs

由图10可知，膨胀应变对钢筋混凝土双向板的 火灾行为有非常重要的影响.

对比任一个板的变形值，基于Eurocode 2模型的变形计算值始终是最大的，而基于Lie模型的变形计算值始终是最小的，Nechnech膨胀应变模型的变形居中；相应地，耐火极限值分别为最小、最大和居中.另外，在后期阶段，基于Lie模型的计算时间－变形曲线比较平缓，相反，其他2个模型的时间－变形曲线比较陡峭，变形速率较快.

上述现象的主要原因在于Eurocode 2模型计算的膨胀应变始终较大，Lie模型的膨胀应变始终较小，如图9所示.可知，较大的膨胀应变，特别是混凝土膨胀应变，会引起较大的应力，从而导致受压区较大的塑性变形和受拉区更多的开裂，最终使得板的变形和刚度退化较大，过早地破坏.

6 结 论

根据大挠度单元理论和热弹塑性本构模型，对钢筋混凝土双向简支板的火灾行为进行了数值分析，主要结论有：

1）建立混凝土双轴受压状态的瞬态热应变计算模型，提出瞬态模量的概念，通过试验验证了模型的有效性及瞬态热应变的重要性.

2）瞬态热应变对钢筋混凝土双向板的火灾行为有重要影响，当不考虑瞬态热应变时，板会过早破坏.

3）膨胀应变是影响钢筋混凝土双向板火灾行为的主要因素之一；数值结果表明，较大的膨胀应变，会导致较大的变形和较小的耐火极限.这一结论还需相关试验数据的验证.

［1］ BAILEY C G.Membrane action of unrestrained lightly reinforced concrete slabs at large displacements［J］.Engineering Structures，2001，23（5）：470－483.

［2］ 王滨，董毓利.四边简支钢筋混凝土双向板火灾试验研究［J］.建筑结构学报，2009，30（6）：23－33.

WANG Bin，DONG Yu-li.Experimental research of four-edge simple support two-way reinforced concrete slab under fire［J］.Journal of Building Structures，2009，30（6）：23－33.（In Chinese）

［3］ LIM L，BUCHANAN A，MOSS P，et al.Numerical modelling of two-way reinforced concrete slabs in fire［J］.Engineering Structures，2004，26（8）：1081－1091.

［4］ 侯晓萌，郑文忠.火灾后预应力混凝土连续板力学性能试验与分析［J］.湖南大学学报：自然科学版，2010，37（2）：6－13.

HOU Xiao-meng，ZHENG Wen-zhong.Experiment on and analysis of the mechanical performance of unbounded pres-tressed concrete continuous slab after elevated temperature［J］.Journal of Hunan University：Natural Sciences，2010，37（2）：6－13.（In Chinese）

［5］ SLUZALEC A.Thermo-elastic-plastic porous material undergoing thermal loading［J］.International Journal of Engineering Science，1999，37（15）：1985－2005.

［6］ 高立堂，宋玉普，董毓利.火灾下钢筋混凝土板的热弹塑性有限元分析——基于S-R分解原理（I：理论）［J］.计算力学学报，2007，24（1）：86－90.

GAO Li-tang，SONG Yu-pu，DONG Yu-li.Thermal-elasticplastic finite element analysis of reinforced slabs under fire based on S-R decomposition theorem （I：Theories）［J］.Chinese Journal of Computational Mechanics，2007，24（1）：86－90.（In Chinese）

［7］ Eurocode 2：Design of concrete structures.ENV 1992：Part 1-2：General rules－structural fire design［S］.Brussels：Belgian Application Document，1996：37－53.

［8］ 过镇海，时旭东.钢筋混凝土的高温性能及其计算［M］.北京：清华大学出版社，2003：16－17.

GUO Zhen-hai，SHI Xu-dong.Behavior of reinforced concrete at elevated temperatures and its calculation［M］.Beijing：Tsinghua University Press，2003：16－17.（In Chinese）

［9］ LIE T，IRWIN R.Method to calculate the fire resistance of reinforced concrete［J］.ACI Structural Journal，1993，90（1）：52－60.

［10］NECHNECH W，MEFAH F，REYNOUARD J.An elastoplastic damage model for plain concrete subjected to high temperatures［J］.Engineering Structures，2002，24（5）：597－611.

［11］ANDERBERG Y，THELANDERSSON S.Stress and deformation characteristics of concrete at high temperatures.Part II：experimental investigation and material behavior model［R］.Bulletin，Sweden：Lund Institute of Technology，1976：51－74.

［12］GERMAY T，FRANSSEN J M.A formulation of the Eurocode 2concrete model at elevated temperature that includes an explicit term for transient creep［J］.Fire Safety Journal，2012，51：1－9.

［13］LI L Y，PURKISS J.Stress-strain constitutive equations of concrete material at elevated temperature［J］.Fire Safety Journal，2005，40（7）：669－686.

［14］HARMATHY T.A comprehensive creep model［J］.Journal of Basic Engineering，1967，89（D3）：496－502.

［15］LIM L，WADE C.Experimental fire tests of two-way concrete slabs［R］.New Zealand：University of Canterbury and BRANZ Ltd，2002：5－41.

［16］王勇.钢框架结构中2×2区格连续混凝土板抗火性能研究［D］.哈尔滨：哈尔滨工业大学土木工程学院，2013：97－102.

WANG Yong.Research on fire-resistant performance of 2×2 grid continuous concrete slabs in a steel-framed structures［D］.Harbin：College of Civil Engineering，Harbin Institute of Technology，2013：97－102.（In Chinese）

Fire Response Analysis of Reinforced Concrete Slabs Considering Transient Strain

WANG Yong1，2†，DONG Yu-li3，YUAN Guang-lin1，WANG Yao4
（l.Jiangsu Key Laboratory of Environmental Impact and Structural Safety in Engineering（China Univ of Mining and Technology），Xuzhou，Jiangsu 221008，China；2.State Key Laboratory for Geomechanics and Deep Underground Engineering（China Univ of Mining and Technology），Xuzhou，Jiangsu 221008，China；3.School of Civil Engineering，Huaqiao Univ，Xiamen，Fujian 361000，China；4.College of Architecture and Civil Engineering，Beijing Univ of Technology，Beijing 100124，China）

Based on the nonlinear temperature field theory，the temperature program of reinforced concrete member was developed.By analyzing the mechanical behavior of different temperature-stress specimens，the transient strain importance was discussed，and the transient strain model under the biaxial stress state as well as transient modulus was proposed.According to the flat shell theory and thermal elasticplastic constitutive model，the finite element model of reinforced concrete two-way slab was established to simulate the fire behavior of the three slabs.In addition，the effect of transient strain and thermal strain on the fire behavior of the slab was studied.The results have shown that the predictions agree well with the test results，and the transient strain model is verified.The parametric study indicates that the transient strain and thermal strain have an important influence on the fire behavior of the slab.

book=64,ebook=97

reinforced concrete slab；fires；transient strain；transient modulus；thermal strain

TU375.4

A

1674-2974（2014）06-0063-07

2013-06-14

国家自然科学基金资助项目（51178143）；中央高校基本科研业务费专项资金资助项目（2014QNA78）；教育部博士学科点专项科研基金资助项目（20120095110027）

王 勇（1984－），男，山东曹县人 ，中国矿业大学讲师，博士

†通讯联系人，E-mail：wangyong06s＠163.com