基于可靠度的输电塔抗风优化研究＊

郑 敏，梁枢果，熊铁华

（武汉大学 土木建筑工程学院，湖北 武汉 430072）

基于可靠度的输电塔抗风优化研究＊

郑 敏，梁枢果†，熊铁华

（武汉大学 土木建筑工程学院，湖北 武汉 430072）

提出一种基于可靠度约束的输电塔实用抗风优化设计方法.首先，识别出体系的失效模式并找出关键杆件同时提取各失效模式对应的安全余量方程，计算各失效模式的可靠指标.然后，对可靠度不满足的失效模式通过加强关键杆件的方法进行优化.最后，对各失效模式进行综合求出体系可靠指标，若体系可靠度满足要求则优化结束，若体系可靠度不满足则通过优化最小可靠指标的失效模式来提高体系可靠度直到满足为止.编制程序对塔架进行了若干个风速的优化，分析结果表明：1）在完整失效路径上存在关键的破坏杆件，对关键杆件进行优化可以有效地提高体系可靠度；2）这是一种直接消除结构薄弱点的优化，优化效果好；3）随优化风速的增大，优化的效率将变低；4）方法计算简单，结果合理.

输电塔；可靠指标；失效模式；优化

塔架结构广泛应用于广播、电视、通信、输电等领域，随着建筑规范的更新，已建的很多塔架已不能满足现行规范的要求，急需对其进行加固；在塔架设计中，为了更好地利用资源也存在优化的问题.格构式塔架的质量较一般高层建筑结构要轻得多，所以一般而言，风荷载对格构式塔架的影响更大，是格构式高耸结构的主要侧向荷载.由于塔架所受风荷载的复杂性以及塔线耦联效应的复杂性，以往塔架优化中所用的风荷载都是一些经验公式［1－3］，降低了优化结果的可靠性.结构设计中存在诸多不确定性，如材料强度不确定性、荷载不确定性等等，对其进行基于概率统计的可靠度分析更符合实际，是结构设计理论的研究方向.目前，基于可靠度的结构优化取得了一定的成果，不过大多数只是在构件的层次上［4－8］，认为各个构件同等重要，这种处理对于静定结构当然没有问题，但对于高次超静定的塔架，把所有构件对结构的安全视为同等重要显然是不合理的，将造成材料的浪费.基于体系可靠度的结构优化设计［9－11］理论比较全面、合理，但由于体系可靠度计算的复杂性提高了问题的难度，对于实际结构，通常要进行大量的计算，缺乏实用性.

针对目前输电塔优化存在的不足，本文主要从两方面作了改进.一方面，本文采用的风荷载为由完全气弹模型风洞试验处理得到的等效静力风荷载，更加符合实际.另一方面，由可靠度理论可知，体系可靠指标小于各种失效模式的可靠指标，且体系可靠指标对可靠指标小的失效模式更加敏感.本文提出一种计算量相对较少的可应用于工程实际的基于体系可靠度优化设计法.

1 等效静力风荷载

1.1 风洞试验

本次风洞试验模型为一个输电塔－线体系完全气动弹性模型，依据相似理论进行设计.本次模型设计除了满足几何相似以外，还满足了气动弹性模型最重要的相似参数：Strouhal数相似、弗劳德数相似、弹性参数和惯性参数相似，气弹模型各相似比见表1.本次风洞试验模型的原型是呼高为75m跨度为750m的酒杯塔线体系，塔构件为不同截面尺寸的角钢.

考虑到该塔处于城市郊区，试验中利用塔尖和粗糙单元来模拟B类风场.本试验在西南交通大学XNJD-3风洞进行，风洞截面尺寸22.5m×4.5m，试验段长度36m，最高实验风速可达17m／s.本次试验的采样频率为256Hz，采样时间为2min.本试验总共布置了8个激光位移测点.风洞试验照片以及风向、测点的布置如图1所示，测点所测位移方向垂直于纸面.

表1 输电塔的气弹模型相似比（n＝1∶40）Tab.1 The similar ratios

图1 风洞试验Fig.1 The wind tunnel test

进行了单塔和塔线体系的多个风速下的风洞试验.图1（d）为90°风向角，也进行了0°，22.5°，45°，60°风向角的风洞试验.由于该输电塔线体系中线上的风荷载比塔直接所受风荷载大得多，而90°风向角时由于线的迎风面最大线所受的风荷载也最大，所以90°风向角时的风荷载是塔线体系的控制风荷载.下面的等效静力风荷载是针对90°风荷载情况进行的.

1.2 等效静力风荷载

有关等效风荷载的计算，详见文献［12］，这里仅给出计算结果.这里采用的等效静力风荷载分为平均风荷载和拟静力脉动风荷载两部分.

1.2.1 平均风荷载

1）输电塔直接所受的平均风荷载：输电塔直接所受的平均风荷载，参照《规范》［13］，采用式（1）的形式.

式中：W1为塔架风荷载平均值，N；w10为按10m高的平均风速算得的风压，w10＝0.5·ρ·，N／m2；μz为风压高度变化系数，μz＝ （z／10）α，α由地面粗糙度决定，这里按B类地貌，取α＝0.15；μs1为体型系数，为待拟合参数，与风速无关，z取塔架上各节点的标高，m；Af1为构件承受风压投影面积计算值，m2.

根据试验得到4个顺风向测点位移平均值，按最小二乘法拟合得到μs1＝2.24.

2）线传到塔上的平均风荷载：线传到塔上的平均风荷载只考虑顺风向，且平均地分配到导线的挂线处.线传到塔上的平均风荷载参照《规范》［13］，采用式（2）的形式.

式中：W2为线传给塔架的风荷载平均值，N；μs2为体型系数，为待拟合参数；Af2为线承受风压投影面积计算值，m2；μz为风压高度变化系数，μz＝（z／10）α，α由地面粗糙度决定，这里按B类地貌，取α＝0.15，z取塔架上挂线点的标高，m.

由特定风速下输电塔挂线与不挂线时同一测点平均位移差计算出该风速下的μs2，最后拟合得到：

式中：v为实际结构10m高的风速，m／s.

1.2.2 拟静力脉动风荷载

拟静力脉动风荷载采用模态风振力为基本标架，以广义位移方差为标架值的形式.确定风振响应均方根时先在模型上施加各模态风振力，再由振型分解法的思想按式（8）把各模态风振力下响应汇总得到风振响应均方根.

1）模态选取：为了得到风荷载动力响应中起控制作用的模态，在模型上施加按准定常得到的风压谱.经过计算，得到对于输电塔部分而言，起控制作用的模态有两阶，振型如图2所示，分别为顺风向、横风向以塔变形为主的第一阶模态.

2）模态风振力：单位广义位移下模态风振力按式（4）计算.

其中Fi为单位广义位移下的模态风振力，量纲为［F］／［L］；mi为节点i的质量；φij为第j阶模态振型在第i节点的值；n为塔的节点数；ωj为第j阶模态的自振频率.

3）广义位移方差：根据广义位移（协）方差与测点位移（协）方差的关系［式（5）］，可由测点位移（协）方差Ryij拟合广义位移（协）方差Rqmn.考虑到第一阶主要是顺风向变形，第二阶主要是横风向变形，可不考虑其相关性，两阶可分开拟合.

式中：Ryij为测点位移（协）方差，由风洞试验数据处理得到；φim，φjn为第m和n阶模态振型在i和j测点处的取值，由ANSYS模态提取；k为所选取的模态数；Rqmn为第m 和n阶模态广义位移（协）方差，为待拟合的参数.

图2 所选模态Fig.2 The selected modes

运用最小二乘法，分别由顺风向、横风向的测点位移（协）方差拟合出第一阶、第二阶模态广义位移方差Rq11和Rq22，最后由不同风速下的值拟合得到随风速变化的公式（6）和（7），以便设计中使用.

式中：v为实际结构10m高的风速，m／s；Rq11和Rq22分别为第一阶、第二阶模态广义位移方差，m2.

4）风振响应均方根：有了广义位移方差，按式（8）可以得到各种响应的均方根.

式中：φij为第j模态响应函数在i杆件的值，φij通过模态风振力施加到有限元模型上得到，可以是轴力、剪力、弯矩等内力，也可以是轴向应力、剪应力等应力，或者是其组合.

2 失效模式识别

2.1 构件的破坏准则

由于实际塔架的节点一般采用多个螺栓连接或焊接，这里构件采用梁单元，考虑构件的轴向力和弯矩.参照规范［13］，构件的破坏准则如下.

式中：N，M为杆件的轴力和弯矩；m为构件强度折减系数，对于单肢连接的角钢构件（肢宽＞40mm）取0.70；An为构件净截面面积；mM为受弯构件稳定强度折减系数，对应角钢，取1.0；W 为杆件截面抗弯抵抗矩；f为钢材屈服强度.

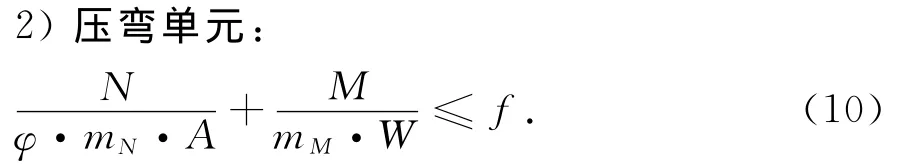
式中：φ为杆件轴心受压稳定系数；mN为压杆构件稳定系数，角钢根据翼缘板自由外伸宽度与厚度比值确定，其他符号同式（9）.各符号的含义及取值详见文献［13］.式（9）和（10）统一写为式（11）.

失效模式识别中，采用的是荷载及强度的平均值，荷载同时考虑自重和风荷载，自重视作确定值.式（11）可写成式（12）的形式.

可看出，在均值意义上，re＞1时杆件安全，re＜1时杆件破坏，re＝1为临界状态.所以在寻找失效模式时，以此为标准来判断单元的失效情况.

2.2 失效模式识别

输电塔属于超静定结构，某一个单元的失效并不意味着结构的失效，只有失效的单元达到一定的数量，形成某一完整的失效模式，结构成为机构，结构才算失效.失效模式的识别参照董聪的全局临界强度分枝－约界法［14］的基本思想进行.

记ck为阶段约界系数，cs为体系约界系数，rmin为各个杆件承载力因子中最小值，rs为最小的体系承载力因子.X为失效模式集合，Xwz为完整的失效模式集合.以下失效模式的识别都是在均值下进行的，为了进行可靠度的计算，在每一步中都计算出顺风向、横风向第一模态风振力下的应力φij1和φij2，以及自重应力σ自重，平均风应力σ平均风，并记录到失效路径X和Xwz中，其中i为破坏阶段号，j为失效模式号.失效模式识别的流程如下：

①置完整失效路径集合Xwz＝φ，置体系承载力因子Rs＝∞，计算初始状态各个杆件的承载力因子并找出其中最小值rmin，把承载力因子re＜ck·rmin的第e个单元加入失效路径集合X中.

②在失效路径集合X中，检查是否形成机构.

③如果形成机构，把该失效路径加入到完整失效路径集合Xwz中.找出该路径上各个杆件各自破坏时的承载力因子的最大值rmax，rmax就是这种失效模式的承载力因子R，而rmax对应的杆件即为该失效模式的关键杆件，判断该杆件破坏时的阶段即为该失效模式破坏的关键阶段.如果该R值比体系承载力因子Rs小，更新体系承载力Rs为R，同时把该路径从失效路径X中删除.

④如果未形成机构，把失效路径上的单元从结构中删除，对于受拉破坏的杆件，删除杆件的同时，在杆件两端的节点处加上沿杆件长度的力以模拟受拉破坏后的屈服后拉力.计算剩余各个杆件的承载力因子re，找出其中的最小值rmin，把re＜ min｛ck·rmin，cs·Rs｝ 的杆件加到失效路径上并加入到失效路径X中，同时把原来的失效路径从失效路径集合中删除.

找到所有的完整失效路径Xwz就是各种失效模式，且Xwz中还包含失效路径上破坏单元对应的σ自重，σ平均风，φij1，φij2等信息，为可靠度计算做好准备.

3 可靠度计算

后面的计算假设随机变量均为正态分布，可靠度均用可靠指标β来表示.

3.1 破坏阶段安全余量方程

3.1.1 安全余量方程提取

式中：j为失效模式号；i为失效路径上破坏阶段号；fy为钢材屈服强度，为一随机变量；σ自重为自重应力，为一确定变量，由2.2部分得到；σ平均风为平均风应力，为一确定变量，由2.2部分得到；φij1，φij2分别为顺风向、横风向第一模态应力振型在破坏单元的取值，由2.2部分得到；q1，q2分别为顺风向、横风向第一模态广义位移，为随机变量.

关于fy，以Q345为例，Q345表示屈服强度标准值fybz为345N／mm2，是具有95%保证率的屈服

可靠度是指可靠的程度，用可靠指标β表示，它与失效概率pf的关系如式（14）所示.强度的较低值，则屈服强度平均值可按式（16）得到：

q1，q2为顺风向、横风向第一模态广义位移，均值为0，由文献得到了顺风向、横风向第一模态广义位移的均方差Rq11和Rq22，且不考虑两模态的相关性，故q1和q2为相互独立的随机变量，均方根σq1和σq2可由式（18）和（19）确定.

3.1.2 安全余量方程标准化

3.2 单个失效模态可靠指标

某失效模式的各个阶段属于并联，只有所有阶段都破坏了才形成失效模式，即结构按某失效模式失效的条件是该失效模式各个阶段的安全余量方程均小于0，发生第j失效模式应满足式（22）.

式中：m为失效阶段数.可以用逐步等效线性化Johnson求交法来得到第j失效模式的等效安全余量方程.关于该求解方法详见文献［15］.计算得到的第j失效模式等效安全余量方程如式（23），式中系数满足式（24）.

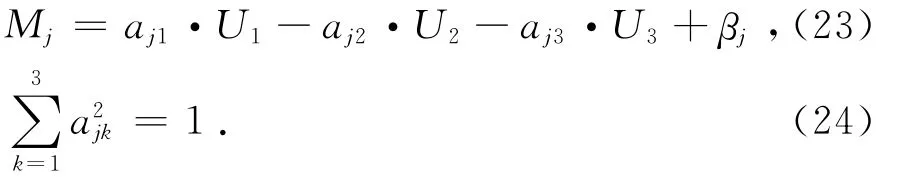
式中：βj为第j失效模式的可靠度指标.

3.3 体系可靠指标

体系的各种失效模式属于串联，只要有一种失效模式形成，结构即告破坏.不过如果从结构安全角度来看，各种失效模式也是并联，只有所有的失效模式都安全，结构才安全，即结构安全应满足式（25）.

4 塔架优化

4.1 优化模型

这里做体系可靠指标满足要求的结构质量增量最小的优化，即

其中：Ai为需要优化的失效模式对应的关键杆件的截面；m为需要优化的关键杆件个数；Ai必须在｛B1，B2，B3，…，BB｝ 中选取，B为可选取的截 面 类型数目；ΔW （A）为结构的总质量的增量；Ci为与材料、杆件长度有关的系数；Ai0为Ai优化前的截面；β为体系可靠指标，按第3部分计算；βu为目标可靠指标，由结构的安全等级以及破坏的性质确定，具体取值可参见规范［16］.

4.2 优化流程

根据体系可靠指标的两个特点，采用准则法进行优化.第一，由于体系可靠指标一定小于任一失效模式的可靠指标，提出首先把各个失效模式优化到满足目标可靠指标的要求.第二，因为体系可靠指标对可靠指标小的失效模式更敏感，提出在各个失效模式单个可靠指标满足要求的前提下若体系可靠指标不满足则提高最小可靠指标的那个失效模式的可靠指标来优化体系，直到体系可靠指标满足要求为止.其优化流程如下：

5 算例

一呼高为75m的塔架，图1所示为其风洞试验的照片，风场为B类风场，对其在10m高风速分别为19m／s，20m／s，21m／s，22m／s，23m／s，24m／s的情况下进行可靠度下的质量最小化的优化，杆件截面在表2中选取.目标可靠指标取3.7.

表2 截面型号Tab.2 Sections

在风速24m／s范围内进行各风速下基于可靠度的优化，通过数值计算，找到了9种典型的失效模式，如图3所示.

图3 前9种失效模式Fig.3 The first nine failure modes

各失效模式破坏风速、破坏起因详见表3，表中破坏风速对应实际结构10m高的风速.一种典型的失效模式包含多种起因的失效模式，表3中列出的为破坏风速较低的一种情况，而且在失效路径中只给出了主要的失效单元.失效路径所对应的杆件号如图4所示.

表3 各失效模式情况一览表Tab.3 The failure modes

图4 杆件号示意图Fig.4 Element numbers

对于不同的风速要求，对可靠度不满足要求的失效模式进行优化，优化通过加大关键杆件的截面来实现.由于塔架是一个高次超静定结构，优化过程中会产生内力重分布，消除某种失效模式往往有多种途径，而且几种需要优化的失效模式的关键杆件之间往往互相影响，优化时必须综合考虑，在保证承载力的条件下找出使结构质量增加最小的一种优化方案.

表4为各种风速的优化结果，限于篇幅，24m／s的计算结果未列出.表5列出优化的效果，图5为质量增加百分比随优化风速的变化图.可以看出，优化的效果较好，在质量增加不多的情况下，抗风承载力得到了很大提高.也可以看出，随优化风速的增大，质量增加百分比斜率总的趋势是增加的，也就是意味着随着优化风速的增大优化的效果是在变差的，这主要是因为优化风速增加，结构趋于等强度，同样的风速增加时产生的失效模式变多，而且同一种失效模式需要优化的设计变量变多.由表5可以看出，除了因为杆件截面不连续引起的可靠指标稍大一点外（优化风速为19m／s），优化后体系可靠指标均略大于目标可靠指标3.7，优化比较合理.

表4 优化结果表Tab.4 The optimized results

表5 优化效果Tab.5 The optimization effect

图5 优化效果曲线Fig.5 The optimization effect curve

6 结 论

通过本文分析，得到以下结论：

1）在完整失效路径上存在关键的破坏杆件，对关键杆件进行优化可以有效地提高体系可靠度.

2）这是一种直接消除结构薄弱点的优化，优化效果好.

3）随优化风速的增大，优化的效率将变低.这主要是因为随着优化的进行，结构趋于等强度，同样的风速增加时需要优化的失效模式变多，而且同一种失效模式需要优化的设计变量变多.

4）本文提出的基于可靠度的优化方法计算简单，结果合理.

［1］ 田琪凌，伋雨林，陈振，等.500kV输电塔承载能力分析及优化设计［J］.华中科技大学学报：城市科学版，2010，27（1）：64－69.

TIAN Qi-ling，JI Yu-lin，CHEN Zhen，et al.Analysis on the bearing capacity of 500kV overhead iced transmission tower and structural optimization［J］.Journal of HUST：Urban Science，2010，27（1）：64－69.（In Chinese）

［2］ 熊铁华，梁枢果，邹良浩.考虑断线时输电铁塔的失效模式及其极限荷载［J］.土木工程学报，2009，42（11）：86－90.

XIONG Tie-hua，LIANG Shu-guo ，ZOU Liang-hao.Dominant failure modes of transmission towers and the limit loads with wire break off［J］.China Civil Engineering Journal，2009，42（11）：86－90.（In Chinese）

［3］ 熊铁华，梁枢果，吴海洋.某输电线路铁塔覆冰条件下的失效模式分析［J］.计算力学学报，2011，28（3）：468－478.

XIONG Tie-hua，LIANG Shu-guo，WU Hai-yang.Failure modes analysis of a broken down transmission tower under ice loads［J］.Chinese Journal of Computational Mechanics，2011，28（3）：468－478.（In Chinese）

［4］ NOILUBLAO N，BUREERAT S.Simultaneous topology，shape and sizing optimization of a three-dimensional slender truss tower using multiobjective evolutionary algorithms［J］.Computers and Structures，2011，89（23／24）：2531－2538.

［5］ RAO G W.Optimum designs for transmission line towers［J］.Computer and Structreres，1995，57（1）：81－92.

［6］ 方从严，刘宁.基于可靠度的非线性随机优化［J］.水利水电科技进展，2005，25（5）：31－32.

FANG Cong－yan，LIU Ning.Reliability-based structural nonlinear stochastic optimization［J］.Advances in Science and Technology of Water Resources，2005，25（5）：31－32.（In Chinese）

［7］ 王光远，吴波.基于可靠度最优分布的桁架优化设计［J］.哈尔滨建筑工程学院学报，1990，23（2）：10－23.

WANG Guang－yuan，WU Bo.Design of trusses based on optimal reliability distribution［J］.Journal of Harbin Architecture＆Civil Engineering Institute，1990，23（2）：10－23.（In Chinese）

［8］ 黄炳生，王文涛.工程系统可靠度优化的多阶段决策算子法［J］.工程力学，1997，14（1）：69－78.

HUANG Bing-sheng，WANG Wen-tao.Multistage decision operator technique for reliability optimization of engineering system［J］.Engineering Mechanics，1997，14（1）：69－78.（In Chinese）

［9］ NATARARAJAN K，SANTHAKUMAR A R.Reliabilitybased optimization of transmission line towers［J］.Computers and Structures，1995，55（3）：387－403.

［10］方从严，刘宁，卓家寿.结构可靠度优化的敏感性分析［J］.应用力学学报，2005，22（1）：63－66.

FANG Cong－yan，LIU Ning，ZHUO Jia-shou.Structural reliability optimization with sensitivity analysis［J］.Chinese Journal of Applied Mechanics，2005，22（1）：63－66.（In Chinese）

［11］许林.基于结构可靠度的优化设计研究［D］.大连：大连理工大学，2004：27－114.

XU Lin.A study on reliability based structural optimization［D］.Dalian：Dalian University of Technology，2004：27－114.（In Chinese）

［12］郑敏，梁枢果，熊铁华.基于塔线体系气弹模型风洞试验的输电塔风致响应计算［J］.武汉理工大学学报，2013，35（11）：124－131.

ZHENG Min，LIANG Shu-guo，XIONG Tie-hua.Wind-induced response calculation of the tower in transmission towerline system based on wind tunnel tests［J］.Journal of Wuhan University of Technology，2013，35（11）：124－131.（In Chinese）

［13］DL／T 5154—2002架空送电线路杆塔结构设计技术规定［S］.北京：中国电力出版社，2002：9－30.

DL／T 5154—2002Technical regulation of design for tower and pole structures of overhead transmission line［S］.Beijing：China Electric Power Press，2002：9－30.（In Chinese）

［14］董聪.现代结构系统可靠性理论及其应用［M］.北京：科学出版社，2001：62－225.

DONG Cong.Reliability theory and its application in the modern structural systems［M］.Beijing：Science Press，2001：62－225.（In Chinese）

［15］刘宁，李同春.用三维随机有限元寻求结构的最大可能失效模式［J］.水利学报，1996（3）：36－43.

LIU Ning，LI Tong-chun.A method for searching the mostprobable failure mode by on 3-D SFEM［J］.Journal of Hydraulic Engineering，1996（3）：36－43.（In Chinese）

［16］GB 50068—2001建筑结构可靠度设计统一标准［S］.北京：中国建筑工业出版社，2001：1－19.

GB 50068—2001Unified standard for reliability design of building structures［S］.Beijing：China Architecture ＆ Building Press，2001：1－19.（In Chinese）

Study on the Reliability-based Wind Resistant Optimization of Transmission Line Towers

ZHENG Min，LIANG Shu-guo†，XIONG Tie-hua

（School of Civil and Architectural Engineering，Wuhan Univ，Wuhan，Hubei 430072，China），

A practical design method was proposed for the reliability-based wind resistant optimization of transmission line towers.Firstly，the failure modes and their key elements were identified，and their safety margin equations were established.Second，the failure modes with a reliability index of less than the target reliability index were optimized by strengthening its key element.Lastly，the system reliability index was calculated，and the failure mode with the least reliability index would be optimized if the system reliability index was less than the target reliability.An optimization example of a tower under several wind speeds was given and the results show：1）there were key elements in the whole failure path，and the structure would be well strengthened if the key element was strengthened；2）it was a method in which the weak points were eliminated directly to strengthen the whole structure and it was very effective；3）as the wind speed increased，it would be less effective；and 4）the method was simple and its results were reasonable.

towers；reliability；failure modes；optimization

TU312

A

1674-2974（2014）06-0035-08

2013-07-16

国家自然科学基金资助项目（51078296）

郑 敏（1981－），女，浙江金华人，武汉大学讲师，博士

†通讯联系人，E-mail：liangsg＠public.wh.hb.cn