嫦娥三号测距测速雷达回波的数值仿真

叶红霞 金亚秋

（复旦大学电磁波信息科学教育部重点实验室，上海200433）

引 言

自从1969年美国阿波罗11号飞船实现人类首次登月，几十年来，人类通过对月球探测获得了相当丰富的数据，对月球形状大小、轨道参数、近月空间环境、月球岩石类型与化学成分、月球资源与能源、内部结构与演化历史等研究取得了一系列突破性进展.月球将是人类长期进行深空探测的中转站，也是一个庞大的“太空实验室”，重返月球是空间科学发展的必然趋势.2003年欧洲成功发射“智能一号”（SMART-1）探测器，于2006年撞击月球卓越湖地区，取得了丰富的科学成果［1］.2007年日本“月亮女神”（SELENE）探月卫星发射升空，其上搭载了14种高精度仪器对月球构成及其演变进行精确探测（如观测月面地形、研究月面成分和矿物组成、表面和次表面结构、重力场、磁力场、高能粒子环境，以及月球等离子区等），并于2009年成功撞月，其上搭载的月球雷达探测仪（Lunar Radar Sounder，LRS）探月雷达中心频率4～6MHz，探测深度为4～5 km［2］.我国“嫦娥2号（CE-2）”卫星2010年成功发射，在100km高度月球轨道上实现了高分辨率（7 m）全月球立体影像绘制，并在15km高度对未来CE-3预选着陆点虹湾地区进行了1m分辨率成像.即将发射的CE-3将携带软着陆器，对着陆地区的地形地貌、地质构造和月表环境等进行现场探测和取样分析.然而即使相对平坦的虹湾地区，其影像图显示地形坑坑洼洼，遍布米级、几十米、几百米直径的环形坑，同时还有许多分布在环形坑底部、坑壁及坑缘地区的约米级零散石块.由于月球着陆器对地面平整度的要求非常高，有必要凭借高分辨率的数据，开展进一步分析验证并做出最终选择.

选取CE-3着陆点虹湾地区为仿真区域，根据月球表面的地形地貌（高分辨率数字地型模型（Digital Terrain Model，DTM）高程数据）及物理组成（月壤复介电常数），基于大尺度起伏粗糙的基尔霍夫模型（Kirchhoff Analysis KA）进行电磁计算［3-4］，并根据雷达回波模型进行散射系数（Normalized Radar Cross Section，NRCS）分析、高度测量等问题研究.

1 理论分析

1.1 波束建模与数据准备

嫦娥3号测距测速雷达配置有5个天线波束，各波束中心指向的几何关系如图1所示，其中R4和R5相互垂直，R4在主减速初始阶段垂直指向月面，而R5在着陆器姿态快速调整之后垂直指向月面.R1、R2、R3均匀分布在一个半锥角为17°的圆锥上，圆锥轴线、波束R1以及波束R4和R5在同一垂直平面内，圆锥轴线与R5波束中心的夹角为30°.每个天线的波束宽度为6°×6°，雷达工作频率选择X频段（波长3.8cm）和Ka频段（波长8.76 mm）.

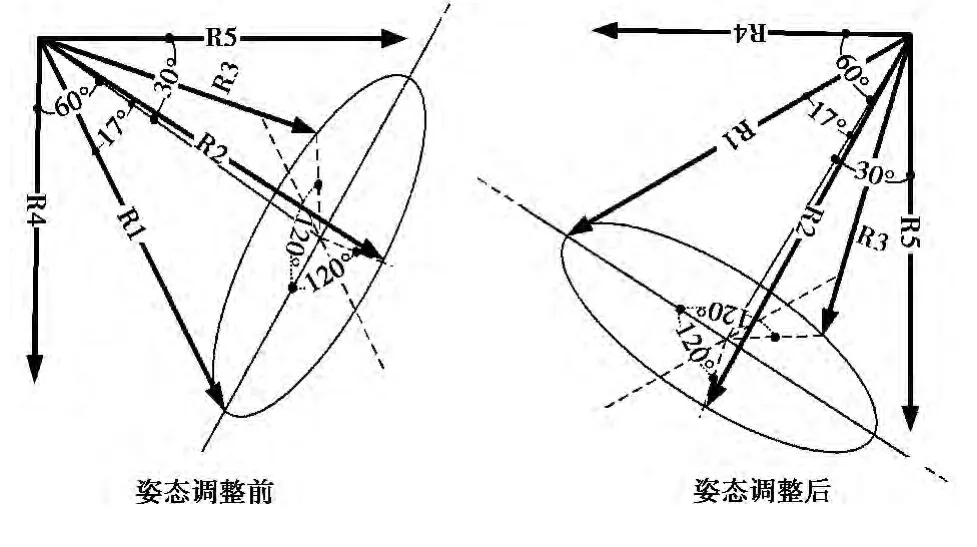
图1 雷达波束模型

为了更好地考虑月面环形山、随机起伏地形等对电磁散射的影响，需要利用尽可能高分辨率的月面高程数据.日本2010年发布了SELENE计划中搭载的月球成像仪／光谱仪（Lunar Imager／Spectrometer，LISM）获取的高分辨率DTM数据，该数据的横向分辨率为7.403m，数据类型为整型.我们选取如图2所示的某局部区域进行模拟仿真，左侧是30m分辨率的地形图，右侧是由两块7.403m分辨率的DTM数据拼凑而成的精细地形图.图3描绘了该区域月面高程沿两个垂直方向上的采样曲线.可以看出：即使看似相对平滑的虹湾地区，由于若干大小不一的环形山起伏的影响，其地形起伏变化很大，不能简单地看成平面模型进行处理.对于本文考虑的X波段λ＝3.8cm、Ka波段λ＝8.76mm而言，横向分辨单元尺寸远大于电磁波长，可考虑大尺度起伏的KA模型来分析这种起伏表面的电磁散射计算.

图2 虹湾地区LISM DTM高程地形

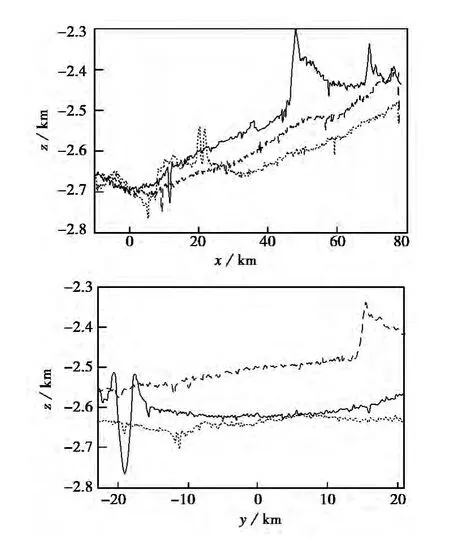
图3 LISM DTM高程沿y和x方向的变化曲线

设雷达局部坐标系内天线辐射场（即粗糙面上的入射场）表示为

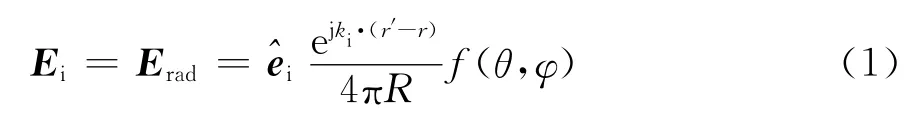
1.2 雷达后向回波计算

根据Huygens原理，在切平面近似和远场近似条件下，粗糙面上任一面元ΔSm在探测雷达位置处的二次辐射场可写成［5］

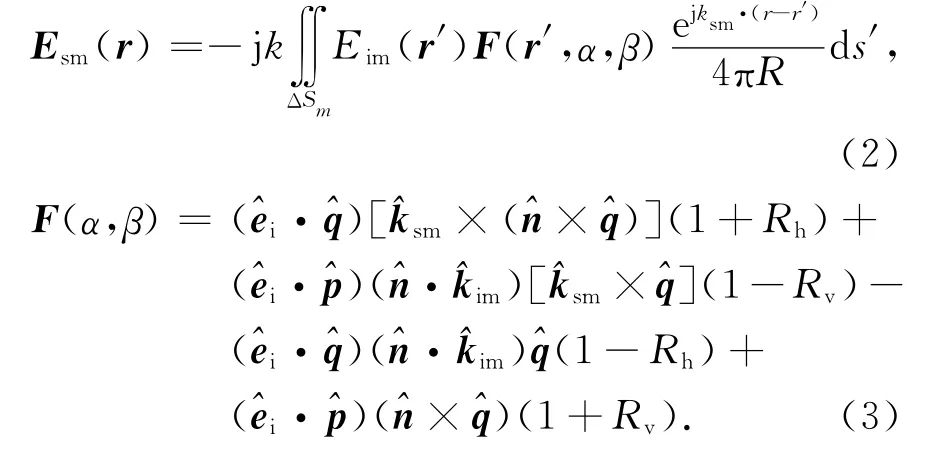
式中：Eim为局部面元照射场的振幅；为粗糙面局部位置的正交坐标矢量，对后向雷达接收和Rv为粗糙面局部区域的水平和垂直极化反射系数.

若忽略每个面元上照射场的幅度变化，只考虑其相位干涉贡献，则总散射场可近似成

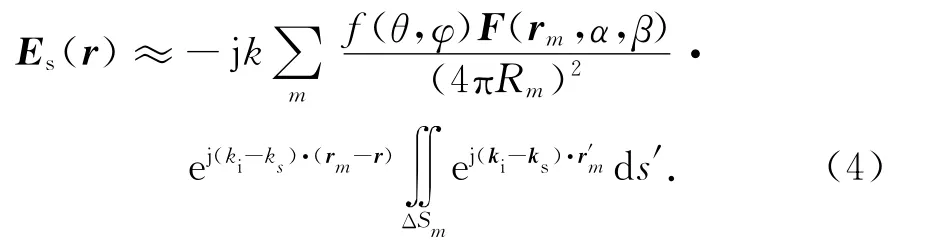
式中Rm＝｜rm-r｜表示面元中心到雷达的直线距离，上式中的相位积分可解析计算为［4］

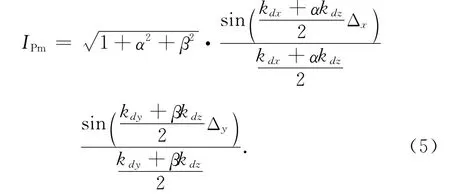
式中：kd＝ki-ks；Δx、Δy为粗糙面的横向离散间隔.这样无需对粗糙面元进一步离散剖分，大大降低计算复杂度.

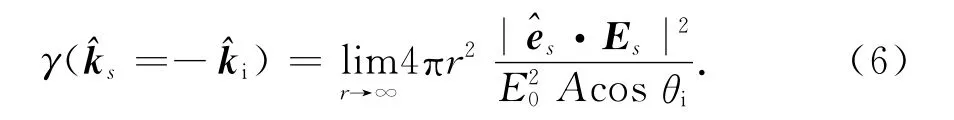
式中r取波束中心点到雷达平台的距离；E0＝1／（4πr）为波束中心点的入射波强度.分别取＝即可得到两种极化的回波功率Pr和归一化散射系数NRCS.

2 实验结果分析

对图2中中心经纬度（N43.0°，E329.7°）的一块局部区域进行数值仿真，图4分别给出了不同波段（Ka波段和X波段）两种极化（VV极化和HH极化）情况下每个雷达波束接收到的回波强度Pr随雷达下降高度的变化曲线.

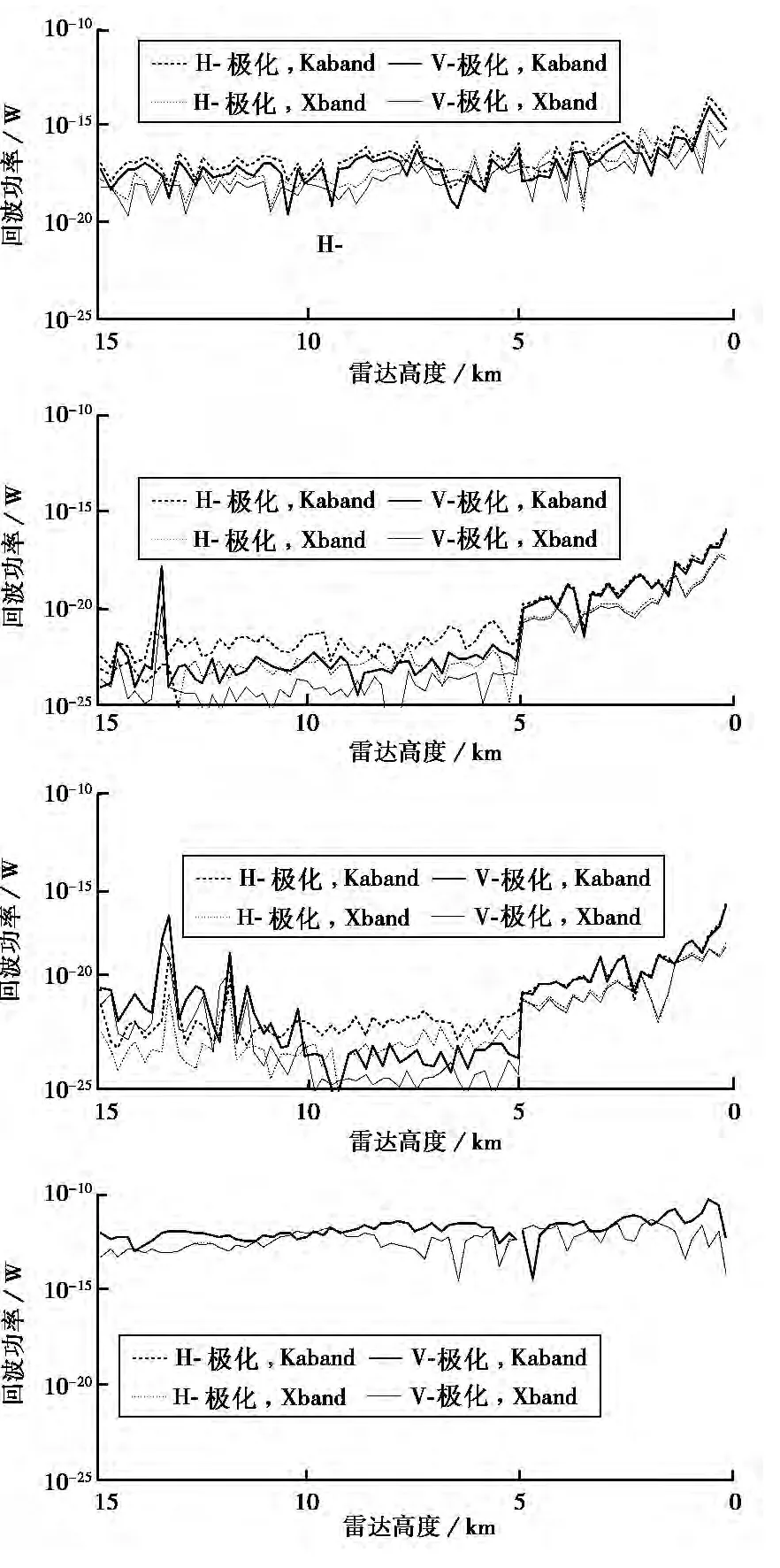
图4 雷达回波功率随雷达高度的曲线

3 结 论

本文根据日本SELENE提供的月球高分辨率DTM数据，基于高频KA方法仿真计算探测雷达下降过程中雷达散射回波，分析雷达高度、波束角、极化、频率等参数回波特性的影响.

［1］FOING B H，HEATHER D J，ALMEIDA M，et al.The science goals of ESA’s SMART-1mission to the moon［J］.Earth，Moon and Planets，2001：523-531.

［2］ONO T，KUMAMOTO A，KASAHARA Y，et al.Lunar radar sounder（LRS）experiment on-board the SELENE spacecraft［J］.Earth Planets Space，2004，52：629-637.

［3］FA W Z，JIN Y Q.Simulation of radar sounder echo from lunar surface and subsurface structure［J］.Science in China（D），2010，53（7）：1043-1055.

［4］YE H，JIN Y Q.A hybrid analytical-numerical algorithm of scattering from an object above a rough surface［J］.IEEE Trans on Geoscience and Remote Sensing，2007，45：1174-1180.

［5］TSANG L，KONG J A.Scattering of Electromagnetic Waves：Advanced Topics［M］.Wiley Interscience，2001.