电离层相位污染和多模传播检测与识别研究

李 雪 柳 文 李吉宁 孙凤娟 李川川

（中国电波传播研究所，山东 青岛266107）

引 言

天波超视距雷达（Over-The-Horizon Radar，OTHR）利用电离层作为传输介质，可实现几千千米外的超视距目标探测.电离层是时变、随机、色散和各向异性的介质，影响雷达信号传播，特别是电离层相位污染、多模传播引起OTHR杂波频谱展宽，严重制约低速目标检测［1］.针对这一问题，近年来开展了诸多研究.

相位污染引起的杂波频谱展宽，主要采用时域估计补偿方法解决，比较流行的算法有最大熵谱估计法［2］、相位梯度 估计法［3］、时频 分析法［4］、特征分解法［5］和分段多项式相位建模法［6］等.

多模传播引起的杂波频谱展宽，主要采用以下三种方法解决：

1）基于二维天线阵列

OTHR采用二维天线阵列，利用俯仰方向上的波束形成使雷达工作于单一传播模式，但为了满足一定的俯仰、方位分辨率，造价极高.

2）基于工作频率选择

OTHR电离层自适应诊断管理系统实时选择合适的工作频率，可以最大可能地避免多模式传播效应.但考虑对探测目标覆盖及环境干扰等信息，有时不能选择出单模工作频率.

3）基于信号处理技术

当不能从天线结构和频率选择上解决多模传播问题时，就需要考虑采用信号处理技术.文献［7］提出利用海杂波循环对消去除多个Bragg峰，从而发现目标.

若电离层相位污染和多模同时存在，上述方法均失效.文献［7］提出利用高分辨时频分布直接实现目标检测.

通过上述分析可以看出，仅存在相位污染、仅存在多模传播以及二者共存抑制方法完全不同.错误地使用不同类型的抑制方法，将无法获得期望的处理增益，甚至会恶化目标检测能力.同时，若回波数据不存在相位污染和多模传播，仍采用解相位污染和解多模处理，不但增加大量的无效数据处理，影响系统的实时性，还可能恶化未受污染的回波数据.

综上所述，若想有效抑制电离层引起杂波频谱展宽，必须实现回波数据下述四类情形检测与识别：

I无相位污染，无多模传播；

II仅存在相位污染；

III仅存在多模传播；

IV相位污染和多模传播共存.

国内外关于这一问题研究较少，文献［8］在满足相邻距离、方位单元污染函数相同模型假设条件下提出一种时间可逆算法检测相位污染，但不能检测多模，无法实现上述四类情形识别.

本文在时间可逆法基础上，提出特征分解法检测多模传播，级联使用时间可逆法和特征分解法实现I、III类情形识别，并可估计传播模式数目.提出了一种基于回波序列Hankel矩阵特性检测相位污染和多模传播算法，可实现I、III类情形识别、模式数目估计，且无需相邻距离、方位单元污染函数相同模型假设.首次提出基于返回散射探测多模传播检测算法，联合时间可逆法或Hankel矩阵算法实现II、IV类情形识别.

1 电离层相位污染检测方法

1.1 时间可逆法检测相位污染

OTHR在进行解电离层相位污染之前，可以通过考察回波信号序列的时间可逆性来检验是否存在相位污染.

假设来自K个相邻距离、方位单元的回波信号受到相同的相位污染.其中第k个距离单元上的回波序列表示为

式中：sk为未受污染的回波序列；D称为模糊矩阵，分别表示为：

式中：TR为脉冲重复周期；N为一个相干积累时间（Coherent Accumulative Time，CIT）内脉冲重复周期的个数.φ（n）（n＝0，1，…，N-1）为相位污染函数.注意φ（n）中不包含任何线性分量，因为线性分量只会使多普勒谱平移，而不是展宽.

用K个回波序列分别构成数据矩阵X的每一列，矩阵的维数是N×K，得到协方差矩阵R＝XXH／K，其时间可逆性指R＝JR＊J，其中J为交换矩阵，JR＊J称为R的时间逆矩阵.回波信号满足时间可逆性的充分必要条件是对角矩阵D也满足该性质，即D＝JD＊J.

充分条件理论推导如下

设RS＝SSH，则

已知RS＝J，则

由于J2＝I（I为单位矩阵），因此，

而

将式（6）代入式（7）得

上式的推导利用了交换矩阵J的性质JH＝J.由式（8）可见，当D＝JD＊J时有

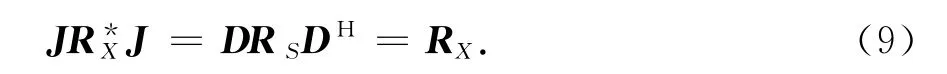
即回波信号满足时间可逆性.

必要条件理论推导如下

左乘D-1，右乘（DH）-1，可得

由此可推出

即

从上述推导可知，当回波信号满足时间可逆性时，对角矩阵D满足时间可逆性，回波信号未经历相位污染；当回波信号不满足时间可逆性时，对角矩阵D也不满足时间可逆性，回波信号存在相位污染.这就给出了回波信号是否存在相位污染的一个判据.实际应用中，通常通过检验信号协方差矩阵的噪声子空间与其时间逆矩阵的信号子空间是否正交来判断.

若杂波频谱展宽由多模传播引起，则未受污染回波序列为

式中r表示模式数目，回波序列协方差矩阵为

即各传播模式自协方差矩阵和互协方差矩阵之和.由于各传播模式回波不相关，故互协方差矩阵为零.而各模式自相关矩阵满足时间可逆性，因此无法利用该方法实现多模传播检测.

1.2 特征分解法检测多模传播

根据现代谱估计理论，信源数目与回波信号协方差矩阵主特征值数目相对应.若回波不存在相位污染，考虑一阶海杂波正负峰成对出现，则回波协方差矩阵主特征值数目为传播模式数目两倍.依据此特性可实现多模传播检测及传播模式数目估计.

若回波信号存在相位污染，其时间平稳性受到破坏，即使不存在多模传播，主特征值数目仍为多个，此时该方法不能检测多模传播.显然，单独应用该方法也不能实现上述四类情形识别.

1.3 时间可逆法与特征分解法的级联应用

通过前面分析可以看出，时间可逆法仅能检测相位污染，但不能实现多模传播检测.特征分解法虽能实现多模传播检测，但需已知回波不存在相位污染.

若先利用时间可逆法检测出回波信号未受相位污染，再利用特征分解法检测多模传播，则可实现上述第I、III类情形识别.但正如前面所分析，该方法要求相邻距离、方位单元杂波数据需满足独立同分布序列，污染函数需满足同一性模型假设.

1.4 Hankel矩阵法检测相位污染和多模传播

有时，电离层相位污染较为严重，回波数据不满足相邻距离、方位单元污染函数同一性模型假设.此时，级联算法失效.本文首次提出一种基于回波时间序列Hankel矩阵的相位污染、多模传播检测方法，可实现I、III类情形识别，且无需上述假设条件.

假设信号s（n）由r个时变复正弦分量叠加组成

式中：Ai为信号幅度；φi为信号相位，i＝1，…，r.每条曲线的瞬时频率为

式中：ωi为信号瞬时频率；Ts为采样间隔.

考虑由s（n）时间序列构造的Hankel矩阵：

式中c＝3r表示矩阵列数，文献［9］给出了该矩阵的几个性质.

性质1：当复正弦分量频率为常量时，Hankel矩阵的秩为r.

性质2：当复正弦分量频率是时变时，Hankel矩阵为满秩.

显然，式（16）可用于表示OTHR回波零中频信号，r表示海杂波一阶峰数目.当回波信号存在电离层相位污染时，频率是时变的，回波信号构造的Hankel矩阵为满秩；当回波信号不存在电离层相位污染时，频率是常量，回波信号构造的Hankel矩阵秩为r，因此该方法可用于判断电离层相位污染是否存在.

当不存在电离层相位污染时，根据回波时间序列构造的Hankel矩阵的秩表征了回波信号数目，考虑海杂波一阶峰成对出现，则传播模式数目为r／2.若r／2＞1，则为多模式传播.Hankel矩阵秩的一半为传播模式数目.因此，该方法可用于电离层相位污染不存在情况下的多模传播检测.该方法与级联应用时间可逆法和特征分解法相比，具有更小的计算量，且使用条件更加宽泛.但正如文献［9］指出，该方法易受噪声影响.OTHR地海杂波回波能量较强，杂噪比通常在50dB之上，有时甚至达70～80dB，因此可忽略噪声影响.若由于电离层吸收或工作频率过低引起杂噪比下降时，使用前应先对噪声进行抑制.文献［9］采用奇异值分解方法对噪声进行了抑制，取得较好效果.通过上述分析可以看出，基于时间可逆法和特征分解法的级联算法、Hankel矩阵法均仅能实现I、III类型识别，当电离层存在相位污染时，无法判别多模传播是否存在，即不能实现II、IV类型识别.

1.5 基于返回散射传播模式区提取的多模传播检测

返回散射探测是OTHR最重要的电离层环境探测手段，其探测路径与雷达信号路径相同.通过对返回散射扫频探测结果处理，可获得覆盖区内全频段传播模式信息，图5（c）是典型的两层返回散射电离图.显然，根据各传播模式区域信息，可实现某一工作频率、距离单元回波多模传播检测.该方法与时间可逆法（或Hankel矩阵法）级联使用，可实现II、IV类情形识别.基于返回散射探测传播模式区提取的多模传播检测方法与特征分解法、Hankel矩阵法相比，引入新信息源，在回波信号存在相位污染情形下仍可有效检测多模.但该方法不能准确估计模式模糊区的传播模式数目.

2 实测数据验证

高频返回散射定频探测数据与OTHR回波数据特性相同，可利用其进行上述算法验证.

2.1 I类情形检测与识别验证

图1为某高频返回散射探测站定频地物回波功率谱，工作频率9.656MHz，群距离700km，脉冲重复频率40Hz，相干积累时间12.8s，频谱形成过程中，为了抑制多普勒旁瓣，添加了汉明窗.从图中可获得频谱最高谱峰3dB宽度为0.12Hz，与无相位污染条件下回波频谱宽度理论值0.114Hz几乎相同.可确定该距离单元回波既不存在相位污染，也不存在多模传播，符合I类情形.分别采用Hankel矩阵算法和级联应用时间可逆法、特征分解法处理回波数据，其中Hankel矩阵列数取为9，设A表示回波信号时间逆矩阵信号向量和协方差矩阵噪声向量的内积均值，取K＝0.01表示正交门限值，定义M表示主特征值数目，N表示传播模式数目，判断结果如表1所示.

图1 返回散射定频探测谱图

表1 相位污染、多模传播检测与识别

2.2 II类情形检测与识别验证

图2（a）为2010年3月30日7时31分某高频返回散射探测站定频地物回波频谱数据，工作频率8.726MHz，群距离780km，脉冲重复频率20Hz，相干积累时间51.2s.图2（b）为取前12.8s数据进行相干积累获得的谱图，显然，图形中仅存在一个谱峰，且频谱峰值3dB宽度为0.17Hz，略大于无相位污染条件下回波频谱宽度理论值0.114Hz，故图2（b）所示频谱仅存在较小相位污染，未受多模传播影响.综合上述分析，可确定图2（a）所示频谱存在相位污染，但不存在多模传播，符合II类情形.分别采用时间可逆法和Hankel矩阵算法检测相位污染，其中Hankel矩阵列数取为9，判断结果如表2所示.由于相位污染存在，此时只能采用基于返回散射传播模式区提取检测多模传播.图3为2010年3月30日7时30分55秒探测的扫频电离图，其波束指向与图2（a）相同.图中黑色“＋”为工作频率8.726MHz、群距离780km对应的位置，显然，该距离单元回波为单模传播，判断结果如表2所示.

图2 返回散射定频探测频谱图

图3 返回散射扫频探测图

表2 相位污染、多模传播检测与识别

2.3 III类情形检测与识别验证

图4为2010年5月12日13时45分某高频返回散射探测站定频地物回波功率谱，工作频率8.532MHz，群距离850km，相干积累时间6.4s，脉冲重复频率20Hz.显然，该回波数据存在多模式传播，同时该组试验数据录取于中午时段，电离层较为稳定，且相干积累时间较短，各谱峰3dB宽度与理论值基本相同，故该组数据不存在相位污染，属于第III类情形.分别采用Hankel矩阵算法和级联应用时间可逆法、特征分解法处理回波数据，其中Hankel矩阵列数取为9，判断结果如表3所示.

图4 返回散射定频测谱图

表3 相位污染、多模传播检测与识别

2.4 IV类情形检测与识别验证

图5（a）为2009年5月17日15时31分0秒探测的返回散射探测定频海洋回波功率谱，工作频率12.077MHz，群距离1 250km，脉冲重复频率20 Hz，相干积累时间51.2s.图5（b）为取前6.4s进行相干积累获得的频谱图，其峰值3dB宽度为0.23Hz，略大于理论值，从图中可明显看出存在两个传播模式.综合上述分析，图5（a）所示频谱多模与相位污染共存，属于IV类情形.采用时间可逆法和Hankel矩阵法检测电离层相位污染，其中Hankel矩阵的列数取为12，判断结果如表4所示.由于相位污染存在，此时只能采用基于返回散射传播模式区提取检测多模传播.图5（c）为2009年5月17日15时30分55秒探测的返回散射扫频图.图中黑色“＋”为工作频率12.077MHz、群距离1 250km对应的位置，显然，该距离单元回波存在多模传播.故该回波数据多模传播与相位污染共存.

图5 返回散射扫、定频探测图形

表4 返回散射实测数据相位污染检测

3 结 论

综合应用时间可逆法、特征分解法、Hankel矩阵法、基于返回散射传播模式提取的多模传播检测与识别算法，可实现I、II、III、IV类情形识别，为后续信号处理选择相应类型抑制算法提供依据.实际应用中，首先采用时间可逆法或Hankel矩阵法判别回波数据是否存在相位污染：若不存在相位污染，则采用特征分解法或Hankel矩阵法进行多模传播检测；若存在相位污染，则采用返回散射传播模式提取算法实现多模传播检测.

［1］凡俊梅，焦培南，肖景明.海洋杂波对高频雷达检测海面上低速目标的影响［J］.电波科学学报，1997，12（2）：205-210.FAN Junmei，JIAO Peinan，XIAO Jingming.The sea clutter effect on the low doppler targets detection by HF radar［J］.Chinese Journal of Radio Science，1997，12（2）：205-210.（in Chinese）

［2］BOURDILLON A，GAUTHIER F，PARENT J.Use of maximum entropy spectral analysis to improve ship detection by over-the-horizon radar［J］.Radio Science，1987，22（2）：313-320.

［3］邢孟道，保 铮.电离层电波传播相位污染校正［J］.电波科学学报，2002，17（2）：129-133.XING Mengdao，BAO Zheng.Phase perturbation correction in ionospheric electromagnetic wave propagation［J］.Chinese Journal of Radio Science，2002，17（2）：129-133.（in Chinese）

［4］HOWLAND P E，COOPER D C.Use of the Wigner-Ville distribution to compensate for ionospheric layer movement in high-frequency sky-wave radar systems［J］.IEEE Proceedings-F，1993，140（1）：29-36.

［5］ANDERSON S J，ABRAMOVICH Y I.A unified approach to detection，classification，and correction of ionospheric distortion in HF sky wave radar systems［J］.Radio Science，1998，33（4）：1055-1067.

［6］李 雪，邓维波，焦培南.分段多项式建模解电离层慢径相位污染阶数选择新方法［J］.电波科学学报，2009，24（6）：1-6.LI Xue，DEND Weibo，JIAO Peinan.New orderselect method of polynomial modeling for ionosphere phase perturbation correction［J］.Chinese Journal of Radio Science，2009，24（6）：1-6.（in Chinese）

［7］郭 欣.天波超视距雷达信号处理技术研究［D］.南京：南京理工大学，2004.GUO Xin.Study on Skywave Over-the-horizon Radar Signal Processing［D］.Nanjing：Nanjing University of Scienee and Technology，2004.（in Chinese）

［8］ABRAMOVICH Y I，ANDERSON S J，SOLOMON I S D.Adaptive ionospheric distortion correction techniques for HF skywave radar［C］／／Proceedings of 1996 IEEE National Radar Conference.Ann Arbor，1996：267-272.

［9］DIMONTE C L，ARUN K S.Tracking the frequencies of superimposed time-varying harmonics［C］／／Proceedings of 1990IEEE National Radar Conference，1990：2539-2542.