极化雷达图像目标相干系数判据的检测研究

王海鹏 金亚秋

（复旦大学 电磁波信息科学教育部重点实验室，上海200433）

引 言

合成孔径雷达（Synthetic Aperture Raear，SAR）成像遥感技术在民用与军事领域都得到了广泛的应用［1］.近年来，机载与星载SAR的空间分辨率已达到了分米量级.甚高分辨率（Very High Resolution，VHR）的全极化SAR技术的发展，极大地扩展了SAR信息研究与应用领域.VHR-SAR的应用技术从地面分布性随机目标的分类与识别，逐步发展到特定的立体目标多维信息的检测与识别［2］.

以往在中等分辨率与单极化SAR图像条件下，常用的目标检测算法主要基于图形图像处理方法，如基于概率分布的恒虚警率（Constant False Alarm Rate，CFAR）算法［3］，滤波、形态学算子、小波变换、模糊理论等方法.

全极化SAR提供了目标与环境的复散射矩阵、相干矩阵、实Mueller矩阵等特征函数矩阵.本文首先计算与模拟理想目标的复散射矢量，然后与SAR图像中待识目标的散射矢量进行相干系数判据计算，对该类待识目标进行检测与理想目标的同类识别.在计算与成像模拟时，利用复旦大学电磁波信息科学教育部重点实验室散射计算软件BART，进行理想目标极化散射计算与成像模拟.以此理想目标模拟数据为目标识别样本，对全极化系统Pi-SAR观测海面养殖箱的成像数据，研究其是否同类目标相干系数判据的检测与识别.

1 相干系数判据与目标检测

1.1 目标复散射矩阵与相干系数

式中：Eih、Eiv为水平、垂直极化入射波；Esh、Esv为水平、垂直极化散射波；R为观测点到目标的距离；k为波数.

由互易性原理，单站SAR一般有Shv＝Svh，复散射矢量可写为

本文采用Pauli展开的复散射矢量为

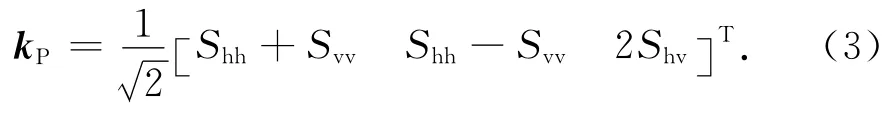
1.2 目标检测算法

对式（2）作归一化，有

设理想目标的归一化散射矢量为ωT，而有待识别是否是同类的检测目标为ωM.两者相干系数定义为［5］

式中：i（ωj）＝k（j＝T，M）表示极化散射特性为ωj的图像；ˉC＝〈kP·k＊TP〉为协方差矩阵.显然，若ωT＝ωM，则两者完全相干，即γ＝1；若两者完全不相干（正交），则γ＝0.实际应用中，受系统噪声等影响，即使是同类目标，γ很难达到1.我们设定阈值T，当γ（ωT，ωM）≥T时，认为两者是同类目标.

本文用两种方法计算式（5）中的γ：一种是直接在实测SAR图像中提取感兴趣目标区域，然后计算其散射特征矢量，再对整幅图像计算γ值，通过阈值滤波，即可获得所检测的目标；另一种是采用仿真的方法，仿真目标散射回波，以仿真结果作为样本，进行目标的检测，下面分别叙述.

2 Pi-SAR实测数据与仿真数据

2.1 Pi-SAR实测数据

Pi-SAR为日本机载SAR系统，携带一个L波段天线（中心频率1.27GHz）和两个X波段天线（中心频率9.55GHz），均可进行全极化测量.在方位向上均做4视处理时，L、X波段分辨率分别为3 m×3m与1.5m×1.5m.图1给出X波段HH图像，地点为日本本州岛（E34.27°，N134.76°），飞行方向自下而上，雷达照射方向自左而右.特别可看到，图中左上面有多个亮度较高的长方形目标，其为人工养殖箱.

图1 Pi-SAR X波段HH极化图像

由Google Earth，图2给出图1区域的光学遥感图像.后续计算均按图2的红框区域（如图2（b））中的目标形状、大小等参数.

2.2 仿真数据

根据Google Earth数据，养殖箱的模型如图3所示，每个大方框为11m×11m，方框间隔4m，材料厚度与高度均为0.5m.因为养殖箱内海浪较小，假定箱内水面为平面.采用本实验室开发的BART软件［6］，计算该类目标模型的复散射矩阵.

图2 海面上人工养殖箱目标

采用的雷达参数和Pi-SAR的一致，飞行高度为12km，中心频率为9.55GHz，带宽为100MHz，入射角为45°，分辨率为1.5m×1.5m.得到的HH极化SAR图像如图3（b）所示.

模拟时，没有考虑系统噪声、海风海浪等可能的影响.模型材质为金属.

图3 养殖箱目标模型及其SAR图像模拟

3 结果分析与展望

3.1 结果分析

为验证检测算法的有效性，先从实测SAR图像中任意选出一个养殖箱图像，作为理想目标样本.并获得其目标散射矢量.然后对于其他养殖箱目标作为待测目标，计算式（3）相干系数.结果如图4（a）所示.

可以看出，大部分养殖箱都可以被检测出来.下面有几个没有被检测到，是因为这些目标与作为训练样本的数据差异过大.

从图1看出，船舶（中间有两艘）和陆地都比较亮.若用CFAR检测，这些亮点是无法消除的.但本文的相干系数检测算法基于目标本身的复散射特性，而不仅是图像灰度值.因此，在目标散射矢量的相干系数检测中，目标材质、大小、形状，以及雷达入射等参数，均纳入了对检测结果的影响.

以图3物理模型作为理想的养殖箱目标，计算其散射矢量，并作为样本，对于SAR图像中所有待测养殖箱目标进行相干系数检测，最终的检测结果如图4（b）所示.

由图4可以看出，对位于图下面的几个养殖箱来说，（b）结果要好于（a）结果.这应该是因为作为理想目标的模拟结果没有受到成像过程中相干斑噪声等影响.

3.2 展望

对于更为复杂的目标识别，合适的目标散射模型与其散射数据库研究，可能是必须的.

复杂目标一般都具有多个散射中心空间分布，如何构建纳入散射中心分布的合适的特征函数与检测，需要进一步的研究.

图4 目标检测结果

［1］SKNOLNIK M I.Introduction to Radar Systems［M］.McGraw-Hill Companies，2001.

［2］JIN Yaqiu，XU Feng.Polarimetric Scattering and SAR Information Retrieval［M］.Singapore：John Wiley and Sons，2013.

［3］ROHLING H.Radar CFAR thresholding in clutter and multiple target situations［J］.IEEE Transactions on Aerospace and Electronic Systems，1983，19（4）：608-621.

［4］CLOUDE S R.Polarisation：Application in Remote Sensing［M］.New York：Oxford University Press，2009.

［5］MARINO A，CLOUDE S R，WOODHOUSE I H.Detecting depolarized targets using a new geometrical perturbation filter［J］.IEEE Transactions on Geoscience and Remote Sensing，2012 50（10）：3787-3799.

［6］XU Feng，JIN Yaqiu.Bidirectional analytic ray tracing for fast computation of composite scattering from electric-large target over a randomly rough surface［J］.IEEE Transactions on Antennas and Propagation，2009 57（5）：1495-1505.