干扰环境下的信号调制识别*
许世宏,梁伟洋
(空军第一航空学院,河南 信阳 464000)
1 引言
通信信号调制制式识别技术的研究一直引起了人们的极大兴趣,经过三十多年的相关研究,目前的研究更趋向实用化,人们重点关注在低信噪比、非高斯等接近真实通信环境下的识别问题[1-4]。以往相关研究大都是基于这样的条件下进行的,即观测样本只包含一种未知的调制类型。随着通信需求的日益增长和通信技术的快速发展,各种民用、军事的无线电台、通信发射设备迅速增多,在有限的无线电通信频谱范围内各种信号分布日益密集,因此不同发射设备发射的无线电通信信号,会不可避免地在相同的频谱上混叠在一起;在无线电通信对抗环境下,敌方为了破坏、阻止我方正常通信,常采用一些人为有意干扰;所有这些因素的存在常常会使接收机在其有限的带宽范围内存在多种调制类型的通信信号。以往很多相关研究成果对这种干扰环境不适合,因此研究这种人为有意干扰、邻道干扰、同道干扰环境下的调制识别问题无论是在理论上还是在实际工程中都具有重要意义。目前,就多种调制信号同时存在情况下的调制识别问题。国内外公开发表的文献很少,仅有几个在非高斯环境下的文献可供参考[2-4]。本文借鉴文献[2]的思想,利用分集技术,首先采用独立成分分析(ICA)获得观测样本矢量的独立分量以消除干扰信号的影响,然后采用以二值支持矢量机(SVM)为基础的多值分类器对观测样本的调制类型进行识别。仿真表明,该算法在低速、中等干扰强度环境下,对调制类型具有较高的识别率。
2 信号模型及调制识别算法描述
假设观测样本来自L个独立的接收天线,第i个天线的接收信号可以表示为
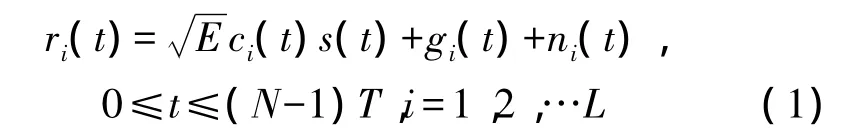

2.1 独立成分分析
独立成分分析(ICA)属于盲信号分离的范畴,它是在没有信源和信道先验信息的情况下,通过对来自多个天线的观测信号进行盲分离,以恢复信源信息的一种技术。把式(2)表示的L个接收天线的信号r1(t),r2(t),…,rL(t)写成向量的形式:
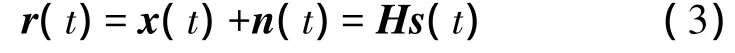
独立成分分析就是在混合矩阵H和独立成分s(t)未知的情况下,寻求分离矩阵 W=[w1,…wN]T,使 y(t)=Wr(t)是对 s(t)的最优估计。从理论上讲W=H-1,但由于混合矩阵H也是未知的,所以需要通过观测样本对其进行估计。由于干扰信号和有用信号来自不同的信源,通过信道卷积变换后,它们是统计独立的。独立成分分析的实现方法有最大似然法和负熵最大化法,负熵最大化法是使对信源信号的估计值之间的互信息最小化,核心思想是寻求观测样本的内在统计独立成分,使y的非高斯性最大化。一般做法是让y与一个标准高斯随机变量v进行比较来判断y的高斯性,即

函数G(u)=-exp(-u2/2)。根据信息论的知识,高斯变量的熵最大,因此负熵的大小可以作为度量变量非高斯性的标准。
根据观测样本矢量求解分离矩阵W有很多算法,其中FastICA算法是通过牛顿迭代使目标函数达到优化的迭代算法,该算法具有稳健性高、收敛速度快等优点,因此本文在寻求分离矩阵时以高阶统计量为基础,采用基于负熵最大化(与非高斯性最大化等价)的快速算法FastICA[6]。
2.2 多值分类器设计
调制类型识别的本质可以看成是一个模式识别问题[7],分类器的设计至关重要。对于多种调制类型的识别问题,一般先进行二值分类,然后再推广到多值分类。支持矢量机(SVM)方法是基于统计学习VC维理论和结构风险最小化原则的一种学习机器,相对于神经网络,它具有较优的分类性能和较好的推广能力。在小样本条件下,支持矢量机能明显缩小经验风险和实际风险的差异,因此SVM在解决小样本、非线性和高维模式识别问题中表现出了特有的优势。该方法的核心思想是通过核函数变换运算,将观测样本向高维空间进行映射,使输入矢量从低维空间变换到高维特征空间,并在这个高维空间中构造能够识别不同调制类型的超平面,以达到识别样本的目的[8]。
对于已知训练样本集合(y1,z1),…,(yi,zi),i=1,2,…,n,y∈Rm,zi∈{+1,-1}用一个超平面(ω·z)-b=0将z1,z2,…,zn没有错误地分为两类(+1或-1),即
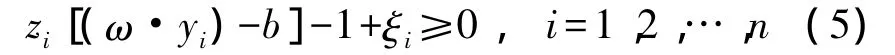
式中,ω=(ω1,ω2,…,ωn)为分类面的权向量系数,ξi是松弛项。为了将寻求最优分类面的问题转化为最优化问题的求解,支持矢量机采用拉格朗日算子求解最优分类超平面,最后得到最优分类函数为[7-8]

支持矢量是指距最优分类超平面最近且平行于该超平面的训练样本,sgn(·)是符号函数,ai为拉格朗日算子。一般用符合Mercer条件的核函数K(yi,x)代替上式中的点积(yi·x),最后得到分类判决函数
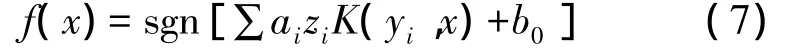
该判决函数就是寻求的支持矢量机,构造SVM的复杂程度与支持矢量的数量有关,这在选择核函数参数时应该注意。
式(7)是个标准二值SVM分类器,将该二值分类器推广到多种调制类型的识别时,涉及二值到多值的推广问题,也就是分类器的组合问题,本文采用投票决策法进行组合分类器设计,其主要思想是:假设待分类的调制类型有N种,将N种类型两两组合,共有N(N-1)/2种组合方式,显然,组合的多少与待识别的调制类型数量的平方密切相关,因此如果调制类型数量较多,为了提高识别速度,一般采用分级的办法减少每组SVM的组合数量,从而提高识别速度。设计每组SVM的多值组合的具体方法是:在第i种类型和第j种类型之间识别时,如果这两种调制类型的二值SVM分类函数大于零,则判定被测样本属于第i种调制类型,给第i种调制类型投一票,否则给第j种调制类型投一票。这样经过多个二值SVM分类判决后,每种调制类型的得票数量不同,选择得票最多的那种调制类型作为对观测样本的最终判决类型。
2.3 识别算法描述
对来自L个接收天线的信号r1(t),…,rL(t)构成观测矢量r,为了得到相应的独立分量,先按下面步骤对该样本矢量进行处理:
(1)中心化:首先对观测样本矢量进行去均值化、中心化处理:r=r-E(r);
(2)白化处理:即对中心化后的样本矢量按珓r=BD-1/2BTr进行变换,其中 B 是 E(r·rT)的特征向量矩阵,D是特征值的对角矩阵(可以验证E)=I),白化后的分量是非相关的;
(3)采用ICA快速算法,求出分离矩阵,进而得到独立样本矢量。
然后再按下列步骤对独立样本矢量进行识别:
(1)将得到的独立样本矢量输入到二值SVM分类器进行识别;
(2)采用投票决策法进行多值分类器组合,选取得票最多的调制类型作为样本的识别类型。
3 仿真分析
为了验证本文算法在干扰环境下的识别性能,在假定观测样本中包含两种未知的调制类型(其中一种是干扰)的情况下,我们对算法进行了仿真验证。调制类型从{2QAM,4QAM,16QAM}中独立等概率选取。采用Jakes信道模型,载波频率取900MHz,码元速率为300ksymbol/s,移动台的移动速度小于10m/s。观测样本来自3个相互独立的接收机,分别在0dB、5 dB、10dB条件下,采集3种调制类型的训练样本,每种条件下采集的训练样本个数为30,完成对SVM的训练。核函数选择径向基核函数K(yi,x)=exp{-|x-yi|2/(2c2)},宽度 c=0.5,c的大小影响支持矢量的个数,因而会对最优分类超面的形成产生影响,从而影响最终的识别性能。
仿真1:该仿真的目的是在给定信噪比的情况下,考查信干比对算法总体识别性能的影响。信噪比为10dB,信干比的变化范围是0dB到20dB。仿真结果如图1所示,可以看出,在观测样本为300、信干比为8 dB时,算法的总体正确识别率大于0.9,随着信干比增加,算法性能逐渐变好。为了对比,图1还给出了在没有干扰存在的情况下算法的性能,可以看出,在信干比大于12 dB时,干扰对算法性能的影响较小。

图1 信干比对算法性能的影响(SNR=10dB)Fig.1 The effect of SIR on modulation classification algorithm when SNR=10dB
仿真2:该仿真的目的是为了考察在衰落信道下算法性能,仿真中采用移动速度的变化来改变信道衰落状况,观测样本为200个和300个,信干比SIR=10dB,信噪比 SNR取10dB,从图2可以看出,当移动速度小于12 m/s时,此时信道属于慢衰落信道,这种情况下算法的识别性能变化较小;随着移动速度的增加,信道衰落变快,信道变化也来越快,由于信道衰落的影响,算法性能越来越差。从图中还可以看出,样本数量越大,信道衰落对算法性能影响越大。
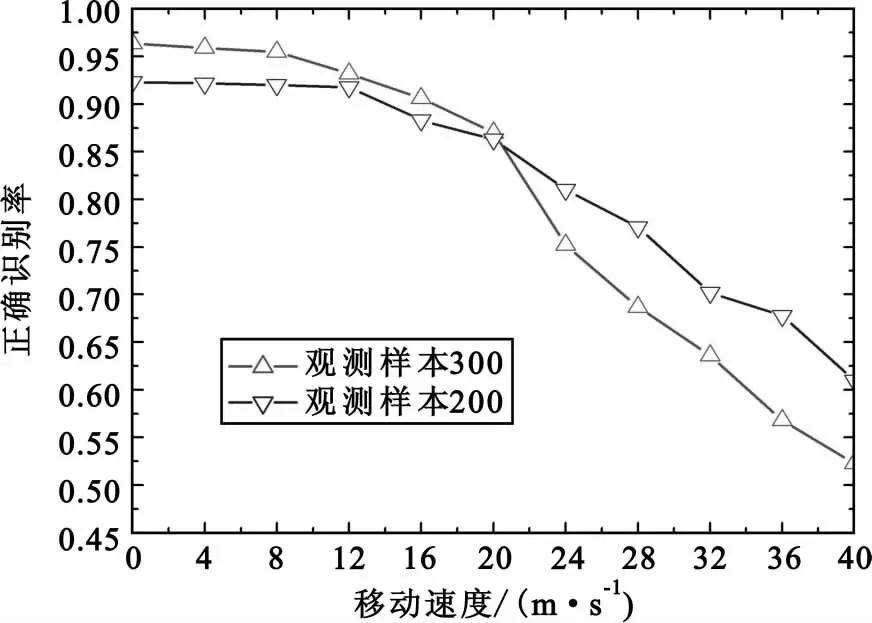
图2 速度对算法性能的影响(SNR=10dB,SIR=10dB)Fig.2 The effect of speed on modulation classification algorithm when SNR=10dB and SIR=10dB
仿真3:该仿真为了研究不同核函数参数对算法性能的影响。由于核函数参数影响支持矢量的个数和最优分类超平面,因此不同的参数会影响算法的性能。表1给出了径向基核函数宽度c和多项式核函数K(xi,x)=((x·xi)+1)d的阶数d对算法性能的影响。观测样本为300,信干比SIR=10dB,信噪比SNR=10dB,可以看出,对径向基核函数,其参数c在0.5时,算法性能最好,随着c的增大或减小,算法性能逐渐变差;而对多项式核函数,当其阶数d为3时,算法识别性能最好;因此合理选择核函数参数是设计分类器的关键因素之一。从表1还可以看出,两种不同的核函数在分别选择合适的参数的情况下,对算法性能没有明显影响。

表1 核函数参数对算法别性能的影响(SNR=10dB,SIR=10dB)Table 1 The effect of kernel function parameters on the performance of algorithm when SNR=10dB and SIR=10dB
4 结束语
本文根据实际工程的需要,在干扰环境下,研究了通信信号调制识别问题,将独立成分分析技术和多天线接收技术引入到信号调制识别领域,提出了一种基于ICA和多值SVM的调制识别算法。研究表明,由于干扰的存在,使观测样本发生了较大变化,为了达到较好的识别性能,对移动速度和信干比等提出了一些限制,如何降低对这些因素的限制以及如何识别更高阶的调制类型是进一步研究应该重点考虑的问题。
[1]Dobre O A,Abdi A,Bar-Ness Y,et al.A survey of automatic modulation classification techniques:classical approaches and new trends [J].IET Communications,2007,4(1):137-156.
[2]Abdi A,Dobre O A,Choudhry R.Modulation classification in fading channels using antenna arrays[C]//Proceedings of 2004 IEEE Military Communications Conference.Monterey:IEEE,2004:211-217.
[3]刘明骞,李兵兵,曹超凤.非高斯噪声下数字调制信号识别方法[J].电子与信息学报,2013,35(1):85-91.LIU Ming-jian,LI Bing-bing,CAO Chao-feng.Recognition Method of Digital Modulation Signals in NonGaussian Noise[J].Journal of Electronics & Information Technology,2013,35(1):85-91.(in Chinese)
[4]崔伟亮,李剑强,江桦.衰落信道盲接收条件下的调制分类[J].电子与信息学报,2011,33(8):1896-1901.CUI Wei-liang,LI Jian-qiang,JIANG Hua.Modulation Classification Algorithm in Fading Channels under Blind Reception Conditions[J].Journal of Electronics & Information Technology,2011,33(8):1896-1901.(in Chinese)
[5]Hyvarinen A,Oja E.Independent component analysis:algorithms and applications [J]. Neural Networks,2000,13(4-5):411-430.
[6]Hyvarinen A.Fast and robust fixed-point algorithm for independent component analysis[J].IEEE Transactions on Neural Network,1999,10(3):626-634.
[7]边肇祺,张学工.模式识别[M].2版.北京:清华大学出版社,2001.BIAN Zhao-qi,ZHANG Xue-gong.Pattern Recognition[M].2nd ed.Beijing:Tsinghua University Press,2001.(in Chinese)
[8]Vapnik V N.An Overview of Statistical Learning Theory[J].IEEE Transactions on Neural Networks,1999,10(5):988-998.

