砌体墙板的平面外性能
倪玉双,杨伟军,梁建国,蒋耀华
(1.长沙理工大学 土木与建筑学院,长沙410114;2.中机国际工程设计研究院有限责任公司,长沙410007)
砌体墙是由块体、竖向灰缝、水平灰缝组成的一种各向异性材料,混合结构房屋中,墙体除了承受墙体平面内的竖向荷载外还承受垂直于墙面的平面外荷载,包括风载和水平地震作用等。它本质上相当于四边有支撑的竖向平板,该平板受到垂直于它表面的荷载,墙体向外弯曲时,在墙体内引起压应力和拉应力,朝向荷载的墙面受压,而另一面受拉。所以将由块体和砂浆组成的砌体墙进行匀质化后即可以采用板的理论来进行研究。
砌体匀质化理论是源于复合材料力学的新兴砌体研究理论,匀质化方法即按照连续体假设,综合考虑块体和砂浆的共同表现,将其几何和材料信息融入到一个等效体中,再将等效体应用到整个结构中的方法。一些学者验证了这一方法推导砌体结构平面内力学性能的可行性[1-9]。中国对砌体墙板平面外抗风与抗震性能的研究很少,而实际地震时砌体墙经常发生平面外破坏。国外一些学者对砌体平面外受力性能做过一些研究。但是结合砌体匀质化方法的研究不多。Mistler等[10]研究了砌体墙平面内、平面外宏观力学性能。Lourenço等[11]分析了在平面外荷载的作用下,墙体尺寸(墙宽和墙高)对砌体结构的影响。Gilbert等[12]进行了无筋砌体墙在平面外低周反复荷载作用下的力学研究。建立了新的力学分析模型,对墙体的总的位移进行动力特性迭代分析,确定了墙体的破坏形式。Lam等[13]提出了一种采用单自由度分析模型研究无筋砌体墙在水平地震荷载作用下的平面外性能的方法。Gabriele等[14]用匀质化方法对平面外荷载作用下的砌体墙进行了极限承载力分析。
本文运用砌体匀质化理论,结合板的理论对砌体墙板的平面外性能进行研究,且本文用薄板理论和中厚板理论两种理论来研究匀质化砌体墙的平面外力学性能,以研究两种理论对不同厚度墙体的适用性,完善砌体分析理论。
1 砌体墙板的匀质化

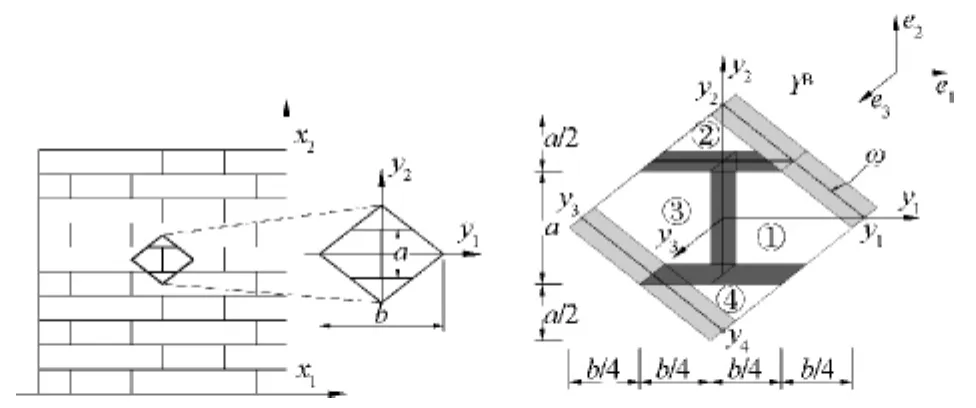
图1 砌体墙板的匀质化单元
2 克希霍夫板(Kirchhoff弹性薄板)
2.1 匀质化模型
薄板的小挠度弯曲理论,以3个计算假定为基础,它的基本内容最早由克希霍夫(Kirchhoff)提出,因此也称为克希霍夫假定,本文称弹性薄板为克希霍夫板。
假设用N= (Nαβ) 表示匀质化板的宏观膜内力场,E= (Eαβ) 为对应的平面内应变场,Eαβ=(U,+U,),M= (M)为匀质化板的宏观平αββααβ面外弯曲应力场,χ= (χαβ) 为对应的平面外应变场,Mαβ=Dαβγδχγδ,U= (Ui)为位移场,其中,Ei3=0,χα,β=-U3,αβ,χi3=0。
则克希霍夫板的匀质化关系式可表达[15]为式(1)。

式中:第1项为平衡条件,表示在基本组元Y上无体积力;第2项和第3项为平面应力的本构方程,它描述了各项材料复合后在组元中的性质,其中grads(uper)表示周期性位移的梯度的对称部分;第4、5项为基本组元的边界条件。
2.2 跨中挠度的计算
对于正交各向异性体,其物理方程为[16]

式中:aij是弹性常数,它们表示单位应力分量引起的形变分量。式中独立的弹性常数只有9个,正应变只与正应力有关,剪应变只与相应的剪应力有关。
正交各向异性薄板在横向荷载的作用下的弹性曲面微分方程为[16]

对于由块体和砂浆组成的砌体墙,匀质化后即可用式(3)进行分析。式(3)中的平面外抗弯刚度可用匀质化后的分量[15,17]代入,则可将弹性力学中经典的弹性曲面微分方程进行变形,即式(3)可变形为式(4)所示形式,U表示挠度。

以四边简支的矩形薄板为例来计算匀质化后的砌体墙板的跨中挠度,其他边界条件的砌体墙板也可采用类似的方法进行,只需要改变相应的边界条件即可。
四边简支板的边界条件为
当x1=0或x1=L时,
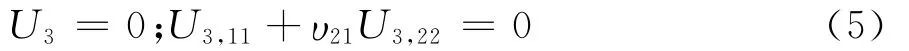
当x2=0或x2=H 时,
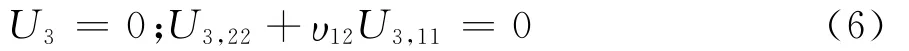
则挠度表示成式(7)所示的形式。
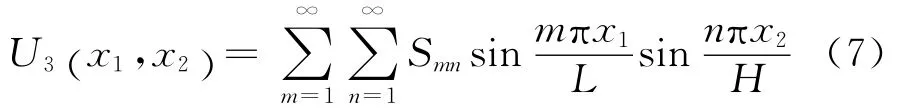
式中:Smn是待求系数;m和n都是任意正整数;L、H分别是板在x1、x2方向的尺寸。
荷载可表示成式(8)所示级数形式

则
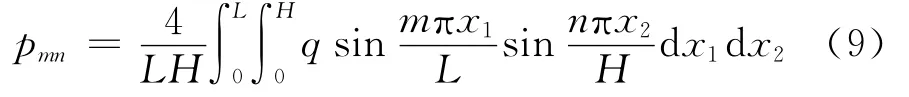
将公式(7)代入微分方程(4)可得

其中

当板横向受均布荷载时,即q (x1,x2)=q,则有

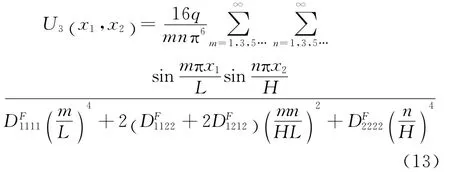
3 瑞斯纳板(Reissner中厚板)
3.1 匀质化模型
经典的薄板理论由于采用了克希霍夫假设,在进行变形几何分析时,忽略了横向剪切变形(γzx,γzy) 对板挠曲的影响,但在建立平衡方程时,却考虑了横向剪力 (Qx,Qy)。
为了探讨横向剪切变形对板挠曲的影响。20世纪三、四十年代以来,以瑞斯纳为代表的一批学者提出了考虑剪切变形的板的理论。一般称为中等厚度板(中厚板)理论(瑞斯纳理论)。在瑞斯纳理论中,引入2个变量U(板的挠度)和Φ(x,y)(瑞斯纳称之为应力函数也称为x方向转角分量φx和y方向转角分量φy),它们分别满足一个4阶方程及一个2阶方程,总阶数为6阶,可以在每一边界给出3个边界条件,而不是经典理论的2个条件[18]。
在瑞斯纳理论中,引入2个变量U和Φ,即3个位移分量和两个转角分量,可表示为UR=((x1,x2) )和Φ = (φα(x1,x2) ),与位移和转角分量相关的应变张量可表示为
宏观平面外弯曲应力M=Mαβ(x1,x2),
剪力Q=Qα(x1,x2),平面内弹性模量与平面外抗弯刚度同克希霍夫板。
即瑞斯纳板的匀质化化模型相对于克希霍夫板而言,只是增加了剪应力和剪应变。
3.2 跨中挠度的计算
对于瑞斯纳板,有如下关系式成立

剪切模量用F= (Fαβ) 表示,则有如式(15)、(16)所示关系式存在。

同时,考虑板的平衡关系,有

采用与克希霍夫板类似的结合弹性力学中经典方程的推导方法,可将式(14)~(16)联合χαβ=(φ,+φ,)代入式(17)和(18)可得式(19)~αββα
(21)。

为便于和弹性薄板进行比较,此处仍以四边简支板为例进行说明,即其边界条件为
当x1=0或x1=L时,

当x2=0或x2=H时,
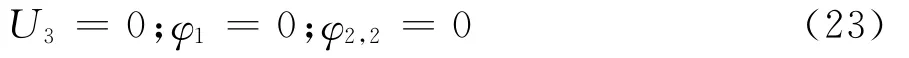
则满足平衡方程和边界条件的函数如下:

将这些函数代入微分方程组,可得

其中:


最后可解得

其中,det (gij)是gij的行列式,由式(24)即可估算板的挠度。其中平面外抗弯刚度取值同克希霍夫板。
4 算例
为验证两种板理论计算的匀质化砌体墙板的跨中挠度的准确性,现将计算值与试验值进行比较。目前中国尚无墙体受平面外荷载的试验数据,其他国家的试验也屈指可数,Lourenco[19]做过几组试验,比较结果见表1。墙体均为四边简支受平面外均布荷载,高均为2 800mm,厚度均为150mm,宽分别为3 400mm(WI)、5 000mm(WII)和5 800mm(WIII),每组墙体3块,试验值为3块墙体的平均值。计算所取材料参数见原文献。
从表1可以看出,两种理论计算值与试验值吻合均较好,且中厚板理论的计算值更接近试验值,对于WI组试验墙体,计算值较其他两组试验墙体更接近于试验值,且随着WI组到WIII组墙体即高宽比减小时,两种理论计算值的误差也越来越小。因为实验墙体只有9片,故结果有其局限性,为进一步探讨2种理论的适用性,进行下面详细的理论分析。

表1 计算值与试验值的比较
5 两种板理论下的跨中挠度计算比较
5.1 不同高宽比下两种理论计算的匀质化砌体墙板的跨中挠度
以由240mm×115mm×53mm的块体砌筑而成,承受q=0.01MPa横向荷载的墙体为例,边界条件及荷载形式如图2所示。利用Matlab软件来计算两种板理论下匀质化砌体墙板的跨中挠度。计算中砂浆的弹性模量为2 200MPa,泊松比为0.25。研究两种板理论计算的跨中挠度误差的规律时,从两个方面来加以讨论:一是固定墙体高度H =3 000mm,计算不同高宽比下每种厚度的墙体的跨中挠度;第二是计算相同高宽比下不同厚度墙体的跨中挠度,最后通过计算结果总结规律。
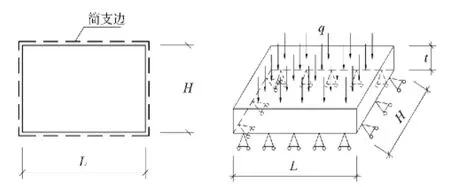
图2 墙体的边界条件和荷载形式
表2表示不同高宽比下各厚度墙体的挠度值,从表2及图3中的分析结果可以看出,120、180、240及370mm的匀质化砌体墙用薄板理论和中厚板理论算得的跨中挠度值随高宽比增大而变化的趋势基本相同,且在固定墙高为3 000mm时,都在高宽比为1.4处误差值高出50%,在高宽比为2时,误差较大,从而可以得出,在利用板理论计算匀质化砌体墙的跨中挠度时,具体采用何种理论要依据墙体的尺寸而定,当两种理论计算值误差较小时,可用简化的薄板理论,但是误差较大时,需用较精准的中厚板理论,中厚板理论更接近墙体的实际力学模型。

图3 不同高宽比下各厚度墙体的挠度误差值
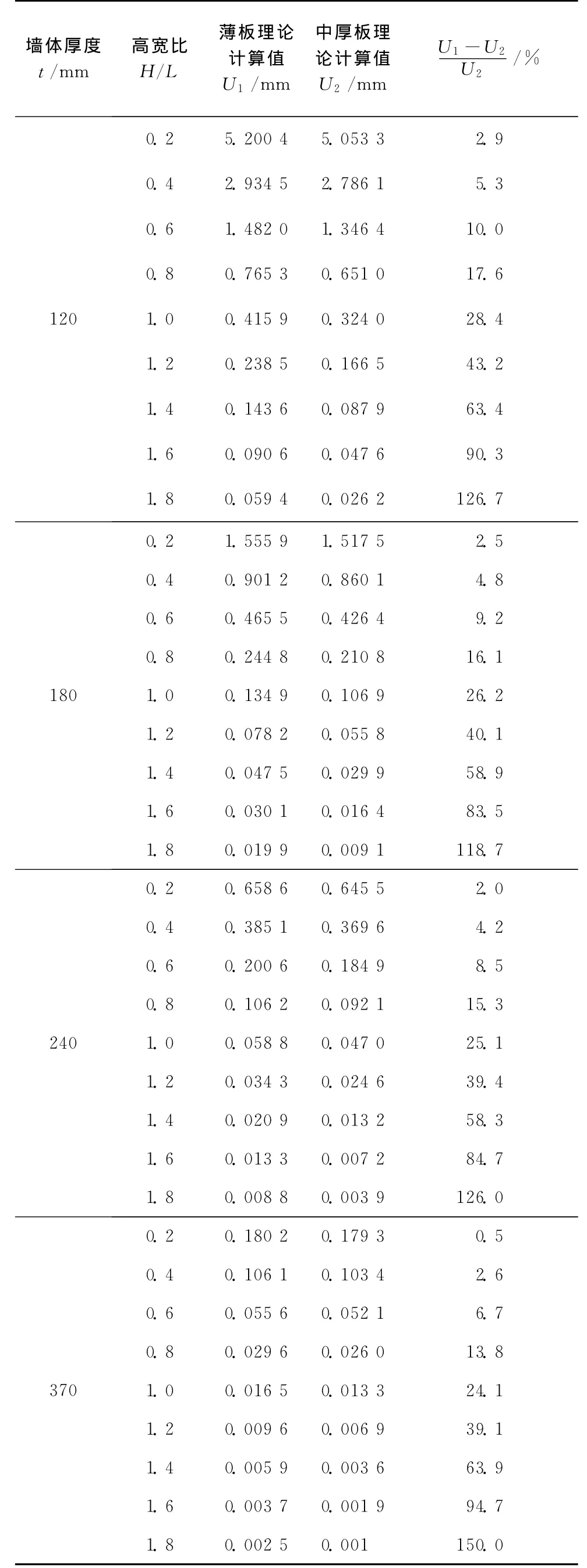
表2 不同高宽比下各厚度墙体的挠度值
5.2 相同高宽比下两种理论计算的墙体挠度
计算相同高宽比下不同厚度墙体的跨中挠度时,仍然以由240mm×115mm×53mm的块体砌筑而成,承受q=0.01MPa横向荷载的墙体为例,墙体边界条件和荷载形式如图2。砂浆的弹性模量和泊松比及其它相关参数同前。
5.2.1 高宽比0.5 由表3中数据和图4中曲线走势可以看出,高宽比为0.5时,两种理论计算的4种厚度墙体的挠度误差值的变化趋势基本一致,随着厚度与宽度或者说厚度与高度比值的增加而减小。且误差均比较小,在10%以内,所以,此时,可用简化的薄板理论来代替中厚板理论计算匀质化砌体墙的跨中挠度。

表3 高宽比0.5时不同厚度墙体的挠度值

图4 高宽比0.5时不同厚度墙体的挠度误差值
5.2.2 高宽比0.75 由表4中数据和图5中曲线走势可以看出,高宽比为0.75时,两种理论计算的4种厚度墙体的挠度误差值的变化趋势基本一致,随着厚度与宽度或者说厚度与高度比值的增加而减小。且误差均比较小,在20%以内,所以,此时,可用简化的薄板理论来代替中厚板理论计算匀质化砌体墙的跨中挠度。

表4 高宽比0.75时不同厚度墙体的挠度值

图5 高宽比0.75时不同厚度墙体的挠度误差值
5.2.3 高宽比1.0 由表5中数据和图6中曲线走势可以看出,高宽比为1.0时,两种理论计算的4种厚度墙体的挠度误差值的变化趋势基本一致,随着厚度与宽度或者说厚度与高度比值的增加而减小,误差均在30%以内。
5.2.4 高宽比1.25 由表6中数据和图7中曲线走势可以看出,高宽比为1.25时,两种理论计算的4种厚度墙体的挠度误差值的变化趋势基本一致,随着厚度与宽度或者说厚度与高度比值的增加而增加,值得注意的是此时误差的变化趋势与高宽比不大于1.0的墙体相比,变化趋势是相反的,从曲线图上的曲线走势也可以看出来,也就是说我们在确定用何种理论计算匀质化砌体墙的跨中挠度时,不光要看墙体厚度与宽度或是厚度的比值,也要考虑墙体的高宽比。

表5 高宽比1.0时不同厚度墙体的挠度值

表6 高宽比1.25时不同厚度墙体的挠度值

图6 高宽比1.0时不同厚度墙体的挠度误差值

图7 高宽比1.25时不同厚度墙体的挠度误差值
5.2.5 高宽比1.5 由表7中数据和图8中曲线走势可以看出,高宽比为1.5的墙体,类同高宽比为1.25的墙体,即两种理论计算的4种厚度墙体的挠度误差值的变化趋势基本一致,都随着厚度与宽度或者说厚度与高度比值的增加而增加。

表7 高宽比1.5时不同厚度墙体的挠度值

图8 高宽比1.5时不同厚度墙体的挠度误差值
6 小 结
用匀质化理论将砌体墙板进行匀质化后用板的理论来研究砌体墙的平面外力学性能,得到了如下结论:
1)通过与试验墙体比较可知,用薄板理论和中厚板理论算得的跨中挠度值与试验值吻合均较好,且中厚板理论计算值更接近试验值。
2)通过进一步的理论分析可知,固定墙高时,120、180、240、370mm的匀质化砌体墙用两种理论算得的跨中挠度值随高宽比增大而变化的趋势基本相同,且在固定墙高为3 000mm时,都在高宽比为1.4处误差值高出50%,在高宽比为2时,误差较大,从而可以得出,在利用板理论计算匀质化砌体墙的跨中挠度时,具体采用何种理论要依据墙体的尺寸而定,当两种理论计算值误差较小时,可用简化的薄板理论,但是误差较大时,需用较精准的中厚板理论。
3)计算相同高宽比下不同厚度墙体的跨中挠度时,要注意高宽比不大于1和大于1两种情况下,两种板理论计算的跨中挠度误差值变化的趋势是相反的,即讨论两种板理论计算的匀质化砌体墙的跨中挠度时,不能单一以某个指标来衡量,要综合考虑墙体厚度,墙体高宽比等。
4)弹性力学中的经典板理论可用来研究砌体墙板的平面外力学性能,但是薄板理论不能模拟所有不同尺寸的墙体,中厚板理论更精准,但是计算复杂,故在不确定是否可用简化的薄板理论时,可先用本文的方法比较二者的跨中挠度计算值,进而确定用何种理论研究其他平面外力学性能指标,即在跨中挠度计算值相差不大的情况下,就可用简化的薄板理论,否则,就需要用计算相对复杂的中厚板理论。
[1]Anthoine A.Derivation of the in-plane elastic characteristics of masonry through homogenization theory [J].International Journal of Solids and Structures,1995,32(2):137-163.
[2]Anthoine A.Homogenisation of periodic masonry:plane stress,generalized plane strain of 3Dmodeling[J].Commun Numer Meth Engng,1997,13(3):19-26.
[3]王达诠,武建华.砌体RVE均质过程的有限元分析[J].重庆建筑大学学报,2002,24(4):35-39.Wang D Q,Wu J H.Finite element analysis of masonry RVE homogenization procedure[J].Journal of Chongqing Jianzhu University,2002,24(4):35-39.
[4]Cavalagli N,Cluni F,Gusella V.Strength domain of non-periodic masonry by homogenization in generalized plane state [J].European Journal of Mechanics A/Solids,2011,30:113-126.
[5]Quinteros R D,Sergio O,Nallim L G.Nonlinear homogenization techniques to solve masonry structures problems[J].Composite Structures,2012,94:724-730.
[6]Milani G,Cecchi A.Compatible model for herringbone bond masonry:Linear elastic homogenization,failure surfaces and structural implementation [J].International Journal of Solids and Structures,2013,50:3274-3296.
[7]王亭,姜忻良,李茂鋆.历史风貌建筑砖砌体加固试验及模拟计算分析[J].工程力学,2012,29(Sup 1):92-96 Wang T ,Jiang X L ,Li M Y.reinforcement experiment and simulation analysis on brick masonry of historical buildings[J].Engineering Mechanics,2012,29,(Sup 1):92-96.
[8]沈继美.砌体匀质化过程的数值模拟方法与应用研究[D].长沙:长沙理工大学土木与建筑学院,2012:44-47.
[9]倪玉双,杨伟军,蒋耀华,等.砌体弹性模量取值的研究[J].四川建筑科学研究,2013,39(1):23-26.Ni Y S,Yang W J,Jiang Y H,et al.Analyses of the elastic modulus values of masonry[J].Building Science Research of Sichuan,2013,39(1):23-26.
[10]Mistler M,Anthoine A,Butenweg C.In-plane and outof-plane homogenisation of masonry [J].Computers and Structures,2007,85:1321-1330.
[11]Lourenço P B,Barros J A O.Size effect on masonry subjected to out-of-plane loading[C]//Proc.12th Int.Brick/Block Masonry Conf,Madrid spain,2000:25-28.
[12]Gilbert M, Hobbs B, Molyneaux T C K.The performance of unreinforced masonry walls subjected to low-velocity impacts: mechanism analysis [J].International Journal of Impact Engineering,2002,253-275.
[13]Lam N T K,Griffit M,Wilson J,et al.Time-history analysis of URM walls in out-of-plane flexure [J].Engineering Structures,2003,743-754.
[14]Gabriele M,Paulo L,Antonio T.Homogenization approach for the limit analysis of out-of-plane loaded masonry walls [J].Journal of Structural Engineering,2006,132(10),1650-1663.
[15]Cecchi A,Sab K.Out-of-plane model for heterogeneous periodic materials:the case of masonry [J].Eur J Mech A/Solids,2002,715-746
[16]徐芝纶.弹性力学[M].3版.北京:高等教育出版社,1990.
[17]Cecchi A,Sab K.Corrigendum to a comparison between a 3Ddiscrete model and two homogenised plate models for periodic elastic brickwork[J].International Journal of Solids and Structures,2006,43(2):390-392.
[18]曲庆璋,章权,季求知,等.弹性板理论[M].北京:人民交通出版社,2000.
[19]Lourenco P B.An anisotropic macro-model for masonry plates and shells:Implementation and validation [R].Portugal:Technical University of Minho and Minho University,1997:36-57.

