考虑损伤累积效应的拱形立体桁架结构倒塌分析
徐 颖,韩庆华,b,芦 燕,b
(天津大学a.建筑工程学院;b.滨海土木工程结构与安全教育部重点实验室,天津300072)
大跨度拱形立体桁架结构作为一种新型空间结构形式,近年在会展中心、体育场馆、车站站台雨棚等大型公共建筑中被广泛应用。作为大型公共建筑,一旦发生连续倒塌破坏,将会带来不可估计的人员伤亡和财产损失,因此研究该类结构在强震作用下的抗倒塌性能十分必要。
文献[1]采用平均反应谱法研究了钢管拱桁架在地震荷载作用下的动力响应,分析了多点激励方式对结构地震响应的影响。文献[2]采用多模态推倒分析方法对钢管拱桁架在罕遇地震作用下的抗震性能进行了研究,并考虑了压杆失稳对结构抗震性能的影响。文献[3]对强震作用下大跨度拱形立体桁架结构的动力失效机理、整体倒塌判别准则进行了研究。文献[4]考虑了损伤累积效应对钢管拱桁架抗震性能的影响。以上研究大多选取单榀拱形立体桁架为研究对象,而整体结构的连续倒塌破坏机理、破坏模式等还有待深入研究。目前,结构连续倒塌分析方法主要包括备用荷载路径法、增量动力分析法等。备用荷载路径法大多局限于钢框架结构[5-7]、钢屋架结构[8]和多高 层 RC 框架结构[9-10]等梁柱结构体系以及具有平面对称性的网格结构[11]体系,忽略了构件失效的原因并需假定失效构件位置。而对于拱形立体桁架结构而言,杆件数量众多,且失效位置并不确定,通过移除某根或某几根杆件并不会引起结构的连续倒塌,采用备用荷载路径法将导致计算量庞大且效率较低。
针对以上问题,本文采用考虑损伤累积效应的方法对拱形立体桁架结构进行倒塌分析。目前适用于钢结构的累积损伤破坏准则主要包括:累积塑性变形准则[12-13]、最大主应变破坏准则[14]和能量耗散准则[15]等。本文采用了累积塑性变形准则,以实际工程为背景,编制了ABAQUS损伤材料子程序,考虑了损伤累积效应和杆件失稳的影响,给出了结构连续倒塌破坏的能量判别准则,研究了该类结构在强震作用下的破坏机理和破坏模式,并分析了损伤累积效应对杆件内力和节点位移的影响。
1 考虑损伤累积效应的材料子程序
1.1 理想弹塑性材料模型
在有限元分析过程中,材料模型的主要任务是实现各增量步之间的应力传递,根据传入的应变增量计算应力增量。对于弹塑性模型,要保证更新后的应力状态满足一定要求。如果在增量过程中发生了屈服,那么更新后的应力状态点应该落在更新后的屈服面上。
应力更新算法主要分为两步,一是弹性试算,二是对弹性试算应力进行塑性修正,确保应力状态点不超过屈服面。
弹性试算时假定当前增量步的应变增量为弹性应变。规定各变量在增量步开始、结束时上标分别为0和t,则σ0表示增量步开始时的应力,σt为增量步结束时的应力。e表示弹性阶段,根据胡克定律有

接下来需要对弹性试算应力进行塑性修正,具体步骤为:
1)计算等效塑性应变增量。等效塑性应变大小由流动法则确定,采用关联流动法则,有

2)根据上一步计算得到的等效塑性应变增量更新应力偏张量

3)增量步结束时,应力张量为更新后的应力偏张量与应力球张量之和。

式中:st为应力偏张量,σmδ为应力球张量。

4)新的等效塑性应变为

1.2 损伤演化及断裂准则
考虑损伤累积效应的弹塑性材料模型需引入一个描述材料损伤程度的变量D。损伤变量D的变动范围在[0,1]。当D=0时,对应无损伤状态;当D=1时,对应材料完全失效。在反复荷载作用下,材料的损伤变量D与材料所经历的塑性应变有关,可用下式[13]表示

材料损伤演化规律描述了材料的刚度退化现象。在有限元分析过程中的任意时刻,材料弹性模量和屈服强度与损伤变量有如下关系:

图1 基本调用关系及流程

式中:ED和E分别为损伤变量值等于D和0时对应的弹性模量值;σ和σs分别为损伤变量值等于D和0时对应的屈服强度;ξ1和ξ2分别为材料系数,对于 Q235钢,ξ1=0.227;ξ2=0.119。
在有限元计算过程中,损伤变量D作为状态变量在各增量步之间传递,通过(10)实现对单元应力的修正。当单元的损伤变量D达到1时,即认为该单元失效,将从整体模型中被移除。损伤材料子程序在ABAQUS中的基本调用关系及流程如图1所示。
1.3 考虑杆件失稳后的计算模型
立体桁架结构在强震作用下,极易发生结构的整体失稳和圆钢管杆件的局部失稳破坏。拱形立体桁架结构的整体失稳可以通过合理设置平面外支撑而避免,但对于圆钢管杆件,当受压达到临界荷载时,承载力突然降低,杆件承载力仅为初始承载力的20%~30%[16],在这种情况下将发生剧烈的内力重分布,如相邻杆件可以承受附加荷载,则只是局部影响,否则压屈扩展将导致动力连续倒塌。
为了考虑杆件失稳的影响,采用图2所示的圆钢管杆单元等效滞回模型[17]考虑杆件失稳后的性能。该模型采用分段线性化办法来描述杆件受压失稳后路径和卸载路径,其中点1和点2的坐标分别为(1,1)、(0,0),其他各控制点坐标与杆件长细比有关,将不同长细比杆件对应的控制点3~9坐标列于表1。

图2 考虑杆件失稳的滞回模型

表1 滞回模型控制点坐标
为准确分析立体桁架结构在地震作用下的动力特性,编写了基于有限元软件ABAQUS显式分析的用户材料子程序。求解过程中,针对各积分点响应调用该程序,材料参数依据子程序所制定的规则执行,可模拟拱形立体桁架结构考虑损伤累积和杆件失稳后性能的弹塑性模型。
1.4 子程序试验验证
采用空间梁单元B31对文献[12]中圆钢管滞回性能试验进行数值模拟,并与试验结果进行对比分析。钢管截面为Φ140×5,长度1.5m,约束条件为一端固定一端自由。在自由端施加恒定轴向压力和水平位移荷载,如图3所示。钢材材料性能如下:弹性模量De=206GPa,泊松比ν=0.3,屈服强度fy=235MPa,极限强度fu=345MPa,极限塑性应变ε=0.2。建立梁单元有限元分析模型并调用用户材料子程序,得到圆钢管滞回曲线如图4所示。

图3 水平位移荷载

图4 圆钢管滞回曲线对比
由于数值模拟不可能与试验条件完全相同,使得计算结果与试验结果存在一定的偏差,但总体吻合较好,说明损伤材料子程序可以很好地实现钢材损伤累积效应的模拟,可用于拱形立体桁架结构损伤累积直至破坏的数值计算。
2 拱形立体桁架结构数值分析
2.1 计算模型
为了研究拱形立体桁架结构在强震作用下的倒塌破坏机理和破坏模式,以某火车站站台雨棚为例(图5),对其进行倒塌分析。该雨棚由若干榀钢管拱桁架组成,跨度为74.6m,全长270.0m,各榀钢管拱桁架间距22.0m,主桁架间设置纵向钢管桁架3道,结构布置如图6所示。

图5 拱形立体桁架结构站台雨棚

图6 结构布置图
主桁架截面形式为正放三角形(图7),节点为钢管直接相贯节点,所有钢材均为Q235B钢材,杆件规格和长细比列于表2。采用ABAQUS进行数值分析时,上下弦杆采用梁单元B31,其余杆件采用桁架单元T3D2,所有节点为铰接节点。结构重力荷载代表值以质量单元的形式施加在相应节点上,其中永久荷载及活荷载分别按1.50kN/m2及0.50kN/m2计算。阻尼采用Rayleigh阻尼,阻尼比取0.05。

图7 主桁架剖面图

表2 杆件长细比
中国 《建 筑 抗震设 计 规 范》(GB 50011-2010)[18]中规定:采用时程分析法时,应按建筑场地类别和设计地震分组选用实际强震记录和人工模拟的加速度时程曲线,其中实际强震记录的数量不应少于总数的2/3。选取天津波、El Centro波以及按规范反应谱拟合得到的人工波作为输入荷载。采用三向输入方式,X向为横向桁架所在方向;Y向为纵向桁架所在方向;Z向为竖直方向。
实际结构设计地震分组为第二组,场地类别为Ⅱ类,场地特征周期值0.40s。按照抗震规范的规定,计算罕遇地震作用时,特征周期应增加0.05s,故特征周期Tg=0.45s。设人工波持时为20s,增强时间T1=5s,衰减时间T2=10s,按照以上参数拟合得到的人工地震波,三向峰值加速度(以下简称PGA)比值为X∶Y∶Z=1∶0.8∶0.6。
2.2 损伤累积效应对杆件内力的影响
为了考察损伤累积效应对强震作用下拱形立体桁架结构杆件内力的影响,选取主桁架柱杆件E100、杆件E101为研究对象(位置见图7),对比分析两种情况下的杆件内力:1)考虑杆件失稳和损伤累积效应(εpu=0.2);2)只考虑杆件失稳不考虑损伤累积效应。对两种PGA:500gal和1 000gal作用下,拱形立体桁架结构的杆件内力响应进行分析,分别对应于结构内部塑性发展较浅和深入的情况。
图8~图9给出了天津波作用下杆件E100和E101的轴向应力、轴向应变时程响应曲线。从图中可以看出,当PGA等于500gal时,结构塑性发展较浅,损伤累积效应还不明显。地震作用初始,两种情况下内力时程曲线完全重合。随着输入地震波峰值的逐渐增大,考虑损伤累积效应使杆件应力幅值略小,应变幅值偏大。当PGA等于1 000gal时,结构塑性发展深入,损伤累积效应十分明显。地震作用初始,两种情况下的应力应变曲线基本重合。随着地震波幅值的增大,杆件刚度下降,杆件应力幅值减小,应变幅值增大。地震作用结束后,杆件E100的损伤累积效应并不明显,杆件内力幅值变化不大,而E101的杆件内力变化较大,应力明显减小而应变明显增大。
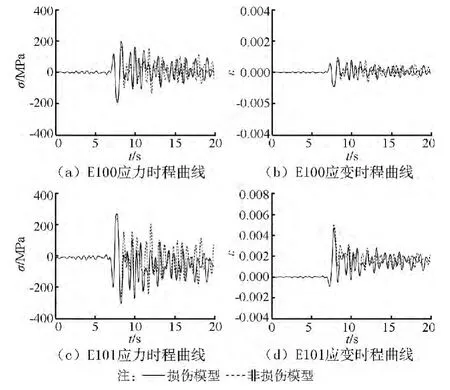
图8 损伤累积效应对杆件内力的影响(PGA=500gal)
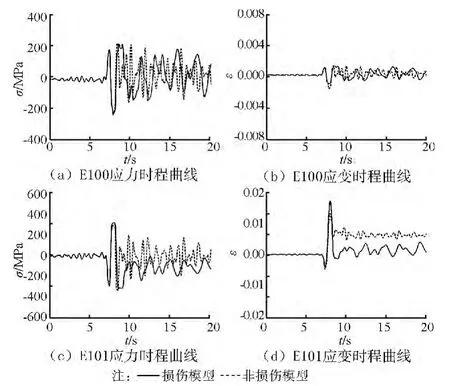
图9 损伤累积效应对杆件内力的影响(PGA=1 000gal)
对应于结构内部塑性发展较浅和深入两种情况,杆件均有塑性应变产生,杆件E100最大压应力幅值约为最大拉应力幅值的0.9倍,杆件E101最大压应力幅值约为最大拉应力幅值的0.8倍,和表1中的材料模型控制参数基本一致,说明所采用的用户材料子程序可以有效模拟杆件失稳后的力学性能。
由于篇幅限制,El Centro波以及人工波作用下杆件的内力时程响应不再赘述,其变化规律与天津波作用下基本一致。现将3种地震波作用下,E100和E101的内力幅值列于表3。考虑损伤累积效应使E100轴向应力减小1%~20%;杆件应变最多增大2.17倍;E101轴向应力减小0.4%~12%,杆件应变增大9%~80%。3种地震波作用下的杆件内力计算结果表明:强震作用下,杆件损伤不断累积,刚度退化,最终失效退出工作。考虑损伤累积效应,使杆件应力幅值减小、应变幅值增大。
2.3 损伤累积效应对节点位移的影响
图10~11给出了主桁架跨中节点N16和主桁架柱节点N98的位移时程曲线(节点位置见图7)。对比分析三向天津波作用下,以下两种情况的节点位移:1)考虑杆件失稳和损伤累积效应;2)只考虑杆件失稳不考虑损伤累积效应。从图中可以看出,当PGA等于500gal时,结构塑性发展较浅,损伤累积效应还不明显,两种情况的节点位移时程曲线基本重合。考虑损伤累积效应时,节点位移幅值略大。当PGA等于1 000gal时,结构塑性发展深入,损伤累积效应明显,节点位移幅值比理想弹塑性情况增大2.5%~7.4%。随着E100和E101的逐渐失效,与之相邻的N98节点所受合力发生改变,位移幅值偏离振动平衡位置并迅速增加。

表3 3种地震波作用下损伤累积效应对杆件内力的影响(PGA=1 000gal)
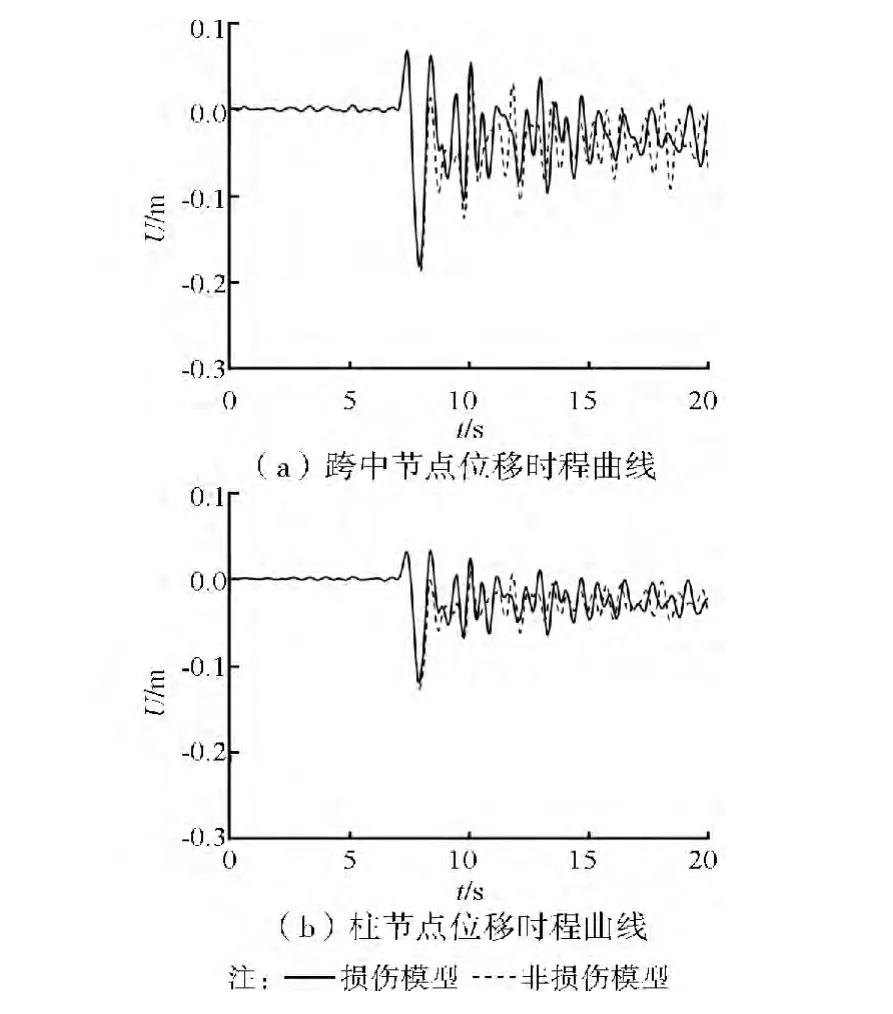
图10 损伤累积效应对节点位移的影响(PGA=500gal)
3 结构连续倒塌过程分析
3.1 结构倒塌破坏判别准则
结构在地震作用下发生倒塌破坏的过程中,初始时地震作用幅值较小,结构应变能在平衡位置附近保持稳定振动状态。结构发生倒塌破坏时,变形迅速增大,塑性耗能剧增,结构应变能迅速增加,以此可作为拱形立体桁架结构发生倒塌破坏的判定准则。
在PGA为1 000gal的三向天津波作用下,拱形立体桁架总应变能时程曲线如图12所示。在6.9s时,结构应变能迅速增加,可认为此刻结构发生倒塌破坏。
3.2 结构倒塌破坏过程分析

图11 损伤累积效应对节点位移的影响(PGA=1 000gal)
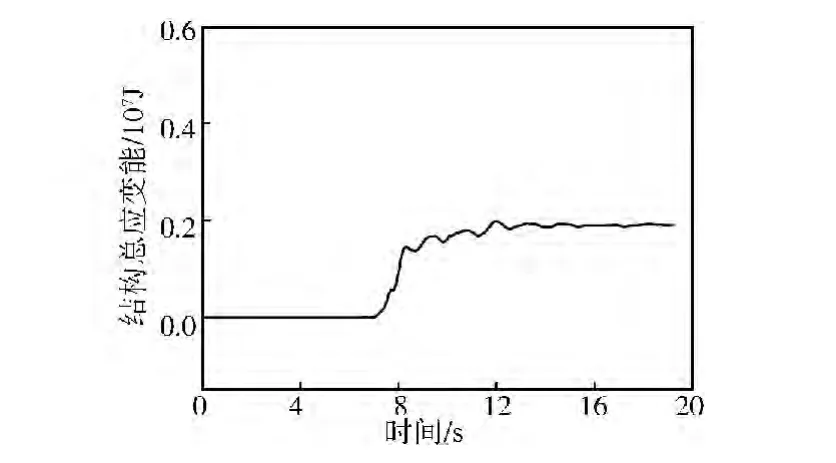
图12 结构总应变能时程曲线
强震作用下,拱形立体桁架结构倒塌破坏变形如图13所示。地震作用初始阶段,加速度幅值较小,拱形立体桁架结构处于弹性状态。随着地震波加速度幅值的逐渐增大,结构杆件受力逐渐增大,部分杆件受压屈曲或受拉屈服产生塑性应变。在地震作用的第6.9s,中间主桁架柱腹杆开始失效退出工作,完全失效杆件将被程序删除。失效区域沿主桁架平面外方向向两端扩展并由柱脚发展至结构顶部。第20s时,地震作用结束,结构发生整体倒塌破坏,各榀主桁架破坏程度基本一致。如图13所示,主桁架失效位置主要集中于桁架柱和1/4跨度处,失效杆件由图14中空心圈表示,主桁架弦杆和纵向桁架杆件均未失效;主桁架失稳杆件由图15中粗实线表示,可知1/4跨度处和桁架柱长细比较大的杆件发生了失稳破坏,考虑杆件失稳的影响,会导致部分杆件提前失效,但对整个结构的破坏模式影响不大。

图13 结构倒塌破坏变形图

图14 主桁架失效杆件示意图

图15 主桁架失稳杆件分布图
4 结论
强震作用下,拱形立体桁架结构杆件损伤不断累积,刚度逐渐退化,最终失效退出工作。随着大量杆件的失效,结构刚度迅速下降,塑性变形逐渐增大,最终发生连续倒塌破坏。
考虑损伤累积效应,使杆件应力幅值减小、应变幅值增大。当PGA等于1 000gal时,杆件E100轴向应力减小1%~2%,轴向应变增大0.38%;杆件E101轴向应力减小3%~5%,杆件应变增大31%~138%。部分杆件失效退出工作后,与之相邻节点所受合力发生改变,导致节点位移幅值偏离振动平衡位置并迅速增加。考虑损伤累积效应时,节点位移幅值比理想弹塑性情况增大2.5%~7.4%。
在三向天津波作用下,中间主桁架柱腹杆最先失效退出工作,随后失效区域由中间沿主桁架平面外方向向两端扩展并由柱脚发展至结构顶部。考虑杆件失稳的影响,会导致部分杆件提前失效,但对整个结构的破坏模式影响不大。
[1]Su L,Dong S,Kato S.Seismic design for steel trussed arch to multi-support excitations [J].Journal of Constructional Steel Research,2007,63(6):725-734.
[2]郑宇淳.大跨度拱形立体桁架的推倒分析[D].天津:天津大学,2007.
[3]韩庆华,芦燕,徐泽民.强震作用下大跨度拱形立体桁架结构动力失效机理研究[J].空间结构,2011,17(4):10-15.Han Q H,Lu Y,Xu Z M.Research on the dynamic failure mechanism of large-span steel arch truss under severe earthquakes [J].Spatial Structures,2011,17(4):10-15.
[4]刘静,李海旺,刘国良,等.强震下钢管拱桁架损伤及失效机理研究[J].土木工程学报,2010,43(1):142-147.Liu J,Li H W,Liu G L,et al.Study on damage and failure mechanism of steel pipe arch truss under strong earthquake[J].China Civil Engineering Journal,2010,43(1):142-147.
[5]Kim J,Kim T.Assessment of progressive collapseresisting capacity of steel moment frames[J].Journal of Constructional Steel Research,2009,65(1):169-179.
[6]Izzuddin B A,Vlassis A G,Elghazouli A Y,et al.Progressive collapse of multi-storey buildings due to sudden column loss-part I: simplified assessment framework[J].Engineering Structures,2008,30(5):1308-1318.
[7]Kwasniewski L.Nonlinear dynamic simulations of progressive collapse for a multistory building [J].Engineering Structures,2010,32(5):1223-1235.
[8]江晓峰,陈以一.大跨桁架体系的连续性倒塌分析与机理研究[J].工程力学,2010,27(1):76-83.Jiang X F,Chen Y Y.Progressive collapse analysis and mechanism study for large-span steel truss structures[J].Engineering Mechanics,2010,27(1):76-83.
[9]梁益,陆新征,李易,等.国外RC框架抗连续倒塌设计方法的检验与分析 [J].建筑结构,2010,40(2):8-12.Liang Y,Lu X Z,Li Y,et al.Verification and analysis on foreign progressive collapse resistance design methods of RC frame structures [J].Building Structure,2010,40(2):8-12.
[10]Sasani M,Sagiroglu S.Progressive collapse resistance of hotel San Diego [J].Journal of Structural Engineering,2008,134(3):478-488.
[1 1]Kim J,Lee Y H.Progressive collapse resisting capacity of tube‐type structures[J].The Structural Design of Tall and Special Buildings,2010,19(7):761-777.
[12]范峰,聂桂波,支旭东.三向荷载作用下圆钢管材料本构模型研究[J].建筑结构学报,2011,32(8):59-68.Fan F,Nie G B,Zhi X D.Constitutive model of circular steel tubes under complicated cyclic load [J].Journal of Building Structures,2011,32(8):59-68.
[13]Shen Z Y,Dong B.An experiment-based cumulative damage mechanics model of steel under cyclic loading[J].Advances in Structural Engineering,1997,1(1):39-46.
[14]Zarrin-Ghalami T, Fatemi A.Cumulative fatigue damage and life prediction of elastomeric components[J].Fatigue & Fracture of Engineering Materials &Structures,2012,36(3):270-279.
[15]Castiglioni C A,Pucinotti R.Failure criteria and cumulative damage models for steel components under cyclic loading [J].Journal of Constructional Steel Research,2009,65(4):751-765.
[16]胡庆昌,孙金墀,郑琪.建筑结构抗震减震与连续倒塌控制[M].北京:中国建筑工业出版社,2007.
[17]谢道清,沈金,邓华,等.考虑受压屈曲的圆钢管杆单元等效弹塑性滞回模型[J].振动与冲击,2012,31(6):160-165.Xie D Q,Shen J,Deng H,et al.Equivalent elastoplastic hysteretic model of steel circular-tube bar elements considering compressive buckling [J].Journal of Vibration and Shook,2012,31(6):160-165.
[18]GB 50011-2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.

