培养小学生数学猜想能力的实践与思考

魏芳

数学猜想是根据已知的事实和数学知识对未知的量及其关系来做出直观的预见性推断。对于小学阶段的学生而言，数学猜想能力的培养极为重要，它不仅能够培养学生归纳整理、独立思考及主动获取知识的能力，同时对于学生探索、创新能力的提高也多有裨益。

一、贴近教材，深入浅出诱发猜想

《义务教育数学课程标准（2011）》在总目标的“数学思考”中明确指出：让学生“在参与观察、实验、猜想、证明、综合实践等数学活动过程中，发展合情推理能力和演绎推理能力，清晰地表达自己的观点”。那么，以教材为载体，以课堂教学为依托，恰当地引导、诱发学生猜想，锻炼学生的创新性思维和创新意识，激发学生的学习兴趣，从而更为透彻地理解和掌握数学知识。

数学猜想包罗万象、深浅不一，基于小学数学阶段的知识积累，应当提供清晰易懂的事例，让学生对它产生兴趣，并引导学生注意观察继而引发合情猜想。例如，在四年级教学“三角形三条边之间的关系”时，可以借用两点间直路和弯路的关系来设问，教师以一条环形的绳索为教具，固定两点套上部分绳索形成直线，剩余部分绳索形成弧线，让学生注意观察，根据学生已有知识得出弯路距离大于直路距离后固定第三点并将弧线套入点上形成一个完整的三角形的其他两条边，并引导学生提炼出“三角形的任意两边之和一定大于第三条边”的数学猜想，并延伸使用长度不同的绳索让学生在一条边不变的情况下组成三角形来观察另外两条边的夹角大小与边长的关系。这样的设计在深入浅出中又不失趣味，同时让学生感受数学猜想就在我们身边。

二、诱导质疑，认知冲突升华猜想

练就学生的质疑能力是培养其数学猜想能力的重点。《学记》有句名言：“学贵在质疑，小疑则小进，大疑则大进，疑者觉悟之机也。”教师重视学生的质疑，正是调动其学习主动性和积极参与学习的重要手段，也是培养学生猜想能力的重要一环。

例如，在教学“轴对称图形”时，学生提出质疑：“是不是所有平行四边形都不是轴对称图形呢？”进而提出：“特殊平行四边形——菱形是轴对称图形”的猜想，这时教师巧妙地升华师生互动中意想不到的生长点，通过立即引导学生剪一剪、折一折、说一说等行之有效的活动进行验证，让学生明确这个猜想是正确的。在实际教学中，往往不可避免地会发生学生原有认知水平与眼前的事实不符的矛盾与冲突，教师应及时找准互动中的生长点，鼓励学生大胆质疑，提出猜想，不怕出错，并以此为资源，准确地加以升华。

叶澜教授针对课堂上的学生质疑猜想打过一个形象的比喻：课堂应是向未知方向挺进的旅程，随时都有可能发现意外的通道和美丽的图景，而不是一切都必须遵循固定线路而没有激情的行程。“大胆的质疑猜想”已成为学生探究未知世界奥秘的便捷的工具。

三、修正猜想，体验合理猜想的喜悦

数学猜想最终都将使用适当的方法进行检验，在验证中判断猜想的正确与否。让学生积极参与，用发散性思维以不同的方法共同进行验证，享受验证过程的乐趣及验证成功的喜悦。

例如，在平行四边形的面积计算教学中，启发学生对新旧知识的转化。

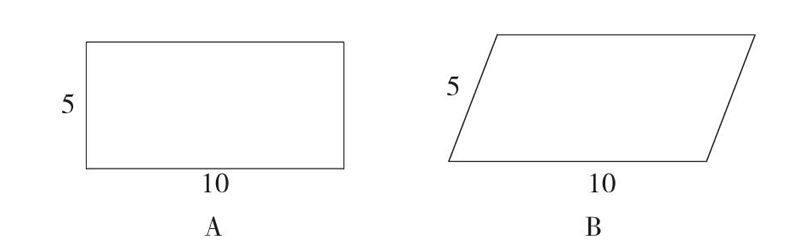
师出示一个长方形（图A）：如何计算它的面积？

生：长方形的面积是长×宽，10×5=50。

师：出示平行四边形（图B），它的面积又该如何计算？

生：我认为和长方形或正方形一样，是两条邻边相乘10×5=50。

师：你是怎么想到的？

生：因为长方形或正方形是邻边相乘，所以我猜想平行四边形面积也可以通过类似的方法来计算。

师：生的猜想有一定道理，但他并没有验证答案的正确性，其他同学还有别的计算方法吗？

生：假设这个平行四边形是一张纸，可以从左上角沿高线方向剪下一个三角形后将其平移到另一边拼成一个长方形，与图A进行比较，如果两图重合就是能确认（生）计算方法是否正确。

生：可以认为这个平行四边形是向一边歪掉的相框，把它扶正就是原来的长方形，因此它的面积一样是长和宽相乘。

教师借助长方形框架将其逐渐拉扁，面积越变越小，引导学生观察思考，让学生直观感受到在周长不变情况下，平行四边形的面积大小一定与高有关。在大家讨论的基础上充分发挥教材的引导功能，用数方格的方法求平行四边形的面积，并发挥多媒体演示的优势，配合学生的猜想，进行归纳与验证，通过将图形剪开、平移、拼补的转化，验证长方形和平行四边形之间的关系，推导出平行四边形计算公式，为继续学习三角形、梯形面积计算奠定基础。

从学生的思维实际出发，顺应学生思路大胆建立猜想，进而验证猜想，让不同层次的学生都有发现、锻炼、创新的机会，多角度地探索问题，多种方法验证“猜想”，从中渗透了科学的思维方法。叶圣陶先生曾说：“教育是什么，往简单方面说，就是培养学生良好的学习习惯。”现在的教学理念也认为：教学不单是传授知识，更重要的是培养学生如何运用知识并主动获取知识的方法，授人以鱼不如授人以渔。

我们提出培养学生数学猜想的能力，其目的并不在于解决如“四色猜想”等世界性的数学难题，而是为了培养学生主动获取知识与解决问题的方法。因此我们在教学实践中应该鼓励学生养成勇于思索、善于猜想的习惯，并通过观察、实验、归纳与类比等获得数学猜想从而最终实现从重结果轻过程向重结果更重知识的形成过程，从重知识积累型教学向发展性创造性教学的转变，使学生能牢固掌握知识并具有创新意识，个人素质得到真正的提高。

（作者单位：福建省福州市铜盘中心小学 责任编辑：王彬）