Existence of Solutions to Generalized Vector Quasi-variational-like Inequalities with Set-valued Mappings

(School of Mathematics and Information,China West Normal University,Nanchong, Sichuan,637002)

Existence of Solutions to Generalized Vector Quasi-variational-like Inequalities with Set-valued Mappings

GAO DA-PENG AND FENG SHI-QIANG∗

(School of Mathematics and Information,China West Normal University,Nanchong, Sichuan,637002)

Communicated by Ji You-qing

In this paper,we introduce and study a class of generalized vector quasivariational-like inequality problems,which includes generalized nonlinear vector variational inequality problems,generalized vector variational inequality problems and generalized vector variational-like inequality problems as special cases.We use the maximal element theorem with an escaping sequence to prove the existence results of a solution for generalized vector quasi-variational-like inequalities without any monotonicity conditions in the setting of locally convex topological vector space.

generalized vector quasi-variational-like inequality,maximal element theorem,upper semicontinuous diagonal convexity,locally convex topological vector space

1 Introduction

Vector variational inequality was fi rst introduced and studied by Giannessi[1]in the setting of f i nite-dimensional Euclidean spaces.This is a generalization of a scalar variational inequality to the vector case by virtue of multi-criteria consideration.Throughout the development over the last twenty years,existence theorems of solutions of vector variational inequalities in various situations have been studied by many authors(see,for example,[2–5]and the references therein).Recently,Peng and Rong[6],Ahmad and Irfan[7]and Xiaoet al.[8]proved some existence theorems of solutions to a class of generalized nonlinear variational inequalities.

In this paper,we introduce a new class of generalized vector quasi-variational-like inequality problems and utilize the maximal element theorem with an escaping sequence to prove the existence of its solutions in the setting of locally convex topological vector spaces (locally convex spaces,in short).Some results of[6–8]are improved and extended.

2 Preliminaries

Let Z be a locally convex space and X be a nonempty convex subset of a Hausdor fftopological vector space E(t.v.s.,in short).We denote by L(E,Z)the space of all continuous linear operators from E into Z and by〈l,x〉the evaluation of l∈L(E,Z)at x∈E.Let L(E,Z)be a space equipped with σ-topology.By the corollary of Schaefer(see page 80 in[9]),L(E,Z)becomes a locally convex space.By Ding and Tarafdar[10],the bilinear mapping〈·,·〉:L(E,Z)×E→Z is continuous.

Let intS and coS denote the interior and convex hull of a set S,respectively,C:X→2Zbe a set-valued mapping such that intC(x)̸=∅for each x∈X,and η:X×X→E be a vector-valued mapping.Let T:X→2L(E,Z),D:X→2X,A:L(E,Z)→2L(E,Z)and H:X×X→2Zbe four set-valued mappings.We consider the following generalized vector quasi-variational-like inequality problem(GVQVLIP,in short):

Find¯x∈X such that¯x∈D(¯x)and for all y∈D(¯x),there exists¯s∈T(¯x)satisfying

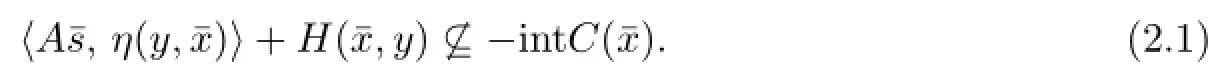
The following problems are special cases of GVQVLIP.

(i)For all x∈X,if D(x)=X,then(2.1)reduces to

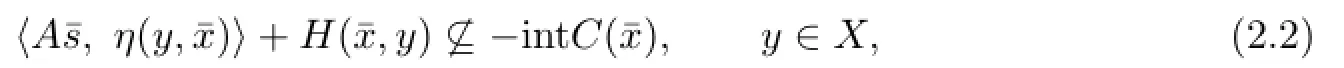
which has been studied by Xiaoet al.[8]

Find¯x∈X,such that there exists¯s∈T(¯x)satisfying(2.2).

(ii)Let A=I be a single-valued mapping and H≡0.Then(2.1)reduces to

which has been studied by Peng and Rong[6].

Find¯x∈X,such that¯x∈D(¯x)and for all y∈D(¯x),there exists¯v∈T(¯x)satisfying (2.3).

For suitable and appropriate choice of the mappings D,T,A,H,η,one can obtain various new and previously known variational inequality problems as special cases(see[6],[8] and the references therein).

In order to prove the main results,we need the following de fi nitions and lemmas.

Let X be a topological space.A subset S of X is said to be compactly open(respectively, compactly closed)in X if for any nonempty compact subset K of X,S∩K is open(respectively,closed)in S.Let Y be a topological space and T:X→2Ybe a set-valued mapping. Then,T is said to be open valued if the set T(x)is open in X for each x∈X.T is said tohave open lower sections if T−1is open valued,i.e.,the set T−1(y)={x∈X:y∈T(x)} is open in X for each y∈Y.T is said to be compactly open valued if the set T(x)is compactly open in X for each x∈X,and T is said to have compactly open lower sections if T−1is compactly open valued.Clearly,each open-valued(respectively,closed-valued)mapping T:X→2Yis compactly open-valued(respectively,compactly closed-valued).T is said to be upper semicontinuous,if for any x0∈X and for each open set U in Y containing T(x0), there is a neighborhood V of x0in X such that T(x)⊆U,for all x∈V;T is said to be closed if the set{(x,y)∈X×Y:y∈T(x)}is closed in X×Y.

(i)a single-valued mappingf:K×K→Zis said to be vector0-diagonally convex in the second argument if

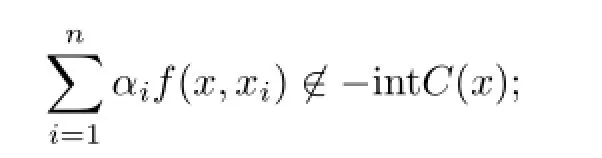
(ii)a set-valued mappingf:K×K→2Zis said to be generalized vector0-diagonally convex in the second argument if

Lemma 2.1[13]LetXandYbe two topological spaces.IfT:X → 2Yis an upper semicontinuous set-valued mapping with closed values,thenTis closed.

Lemma 2.2[14]LetXandYbe two topological spaces,andT:X → 2Ybe an upper semicontinuous set-valued mapping with compact values.Suppose that{xα}is a net inXsuch thatxα→x0.Ifyα∈T(xα)for eachα,then there is ay0∈T(x0)and a subsetyβofyαsuch thatyβ→y0.

Lemma 2.3[15]LetXandYbe two topological spaces.Suppose thatT:X →2Yis a set-valued mapping having open lower sections.Then the set-valued mappingF:X →2Yde fi ned by that for eachx∈X,F(x)=coT(x)has open lower sections.

(i)For eachx∈X,S−1(x)∩Xnis open inXnfor alln=1,2,···;

(ii)For eachx∈X,x̸∈coS(x);

(iii)For each sequenceinXwithxn∈Xnfor alln=1,2,···,which is escaping fromXrelative tothere existn∈Nandyn∈Xnsuch thatyn∈S(xn)∩Xn.Then there exists an∈Xsuch thatS(¯x)=∅.

3 Existence Results

In this section,we prove some existence results of solutions for generalized vector quasivariational-like inequalities without any monotonicity conditions in the setting of locally convex topological vector space.

(A1)for each sequenceinXwithxn∈Xnfor alln=1,2,···,which is escaping fromXrelative tothere existm∈Nandzm∈D(xm)∩Xmsuch that for allsm∈T(xm),

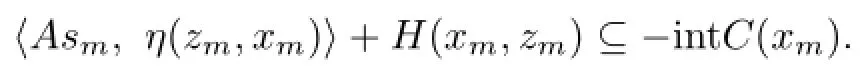
Then GVQVLIP has a solution.

Proof.De fi ne a set-valued mapping P:X→2Xby setting

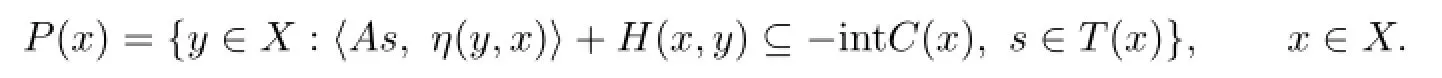
We fi rst prove that x̸∈coP(x)for all x∈X.To see this,by way of contradiction, assume that there existed some point∈X such that∈coPThen there would exist a fi nite subset{y1,y2,···,yn}of X such that for⊆co{y1,y2,···,yn}we have

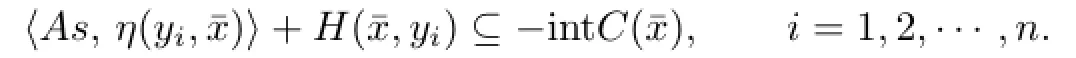
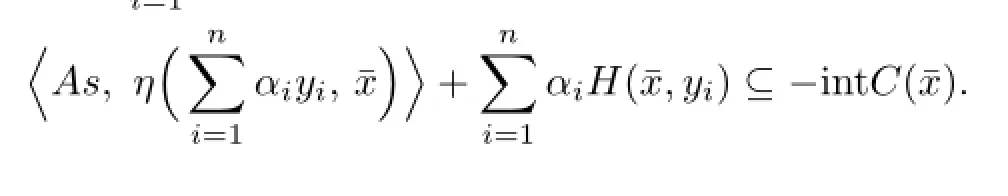
We also de fi ne a set-valued mapping G:X→2Xby {

Then,for each x∈X,G(x)is convex.Suppose that there exists¯x∈X such that∈GIf∈W,then∈D(x)∩coP(x),which contradicts xcoP(x)for all x∈X.If¯xW, then G=Dwhich implies∈Da contradiction.Hence,

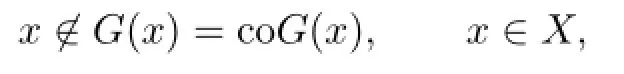
and the condition(ii)of Lemma 2.4 is satis fi ed.

Next,we prove that the set

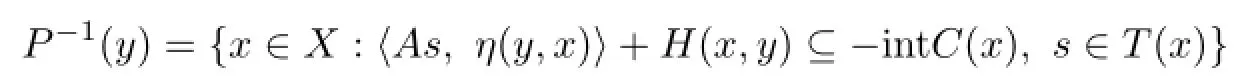
is open for each y∈X.That is,P has open lower sections in X.Consider the set

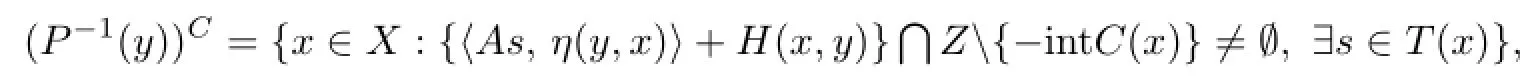
which is the complement of P−1(y).We only need to prove that(P−1(y))Cis closed for all y∈X.Let{xα}be a net in(P−1(y))Csuch that xα→x∗.Then there exists an sα∈T(xα) such that

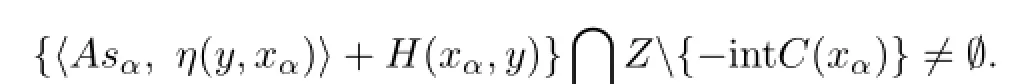
Since T:X→2L(E,Z)is an upper semicontinuous set-valued mapping with compact values, by Lemma 2.2,{sα}has a convergent subset with limit,say s∗,and s∗∈T(x∗).Without loss of generality,we may assume that sα→s∗.Suppose that∩

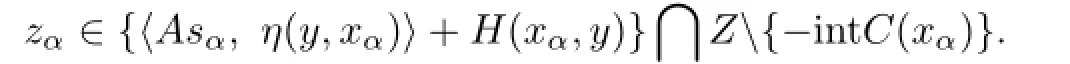
Since〈A(·),η(y,·)〉+H(·,y)is upper semicontinuous with compact values,by Lemma 2.2,there exist a z∗∈〈As∗,η(y,x∗)〉+H(x∗,y)and a subset{zβ}of{zα}such that zβ→z∗.

On the other hand,since Z{−intC(x)}is upper semicontinuous with closed values,by Lemma 2.1,z∗∈Z{−intC(x∗)}.Hence,

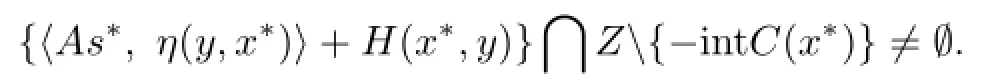
Thus,(P−1(y))Cis closed in X.Therefore,P has open lower sections in X.By Lemma 2.3, coP−1(y)is also open for each y∈X.Since D−1(y)is compactly open for each y∈X,

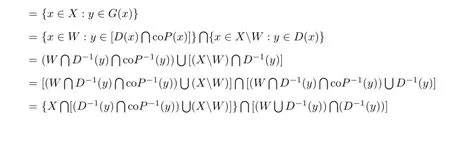
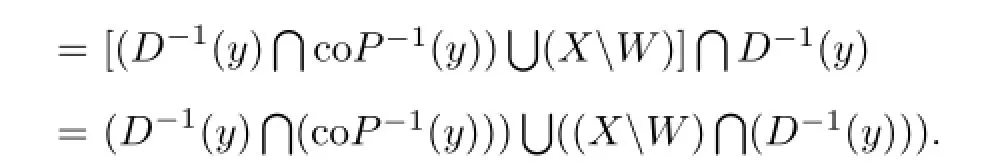
Therefore,G−1(y)also has compactly open values in X for all y∈X,the condition(i) of Lemma 2.4 is satis fi ed.The condition(A1),and implies the condition(iii)of Lemma 2.4. Therefore,by Lemma 2.4,there exists an∈X such that G()̸

Since for each x∈X,D(x)is nonempty,we have¯x∈D()such that D()∩coP()=which implies that∈D()such that D()∩P()=that is,∈D(),and for all y∈D(),there exists an∈T()satisfying〈A,η(y,)〉+H(,y)⊆−intC().

Remark 3.1If D(x)=X for all x∈X,then by Theorem 3.1,we recover Theorem 3.1 in[8].

Theorem 3.2LetEbe a Hausdor fftopological vector space,Xbe a subset ofEsuch thatX=whereis an increasing sequence of nonempty,compact and convex subset ofX,Zbe a locally convex space,andL(E,Z)be equipped withσ-topology,D:X→2Xbe a set-valued mapping with nonempty convex values and compactly open lower sections,the setW={x∈X:x∈D(x)}be closed,C:X→2Zbe a set-valued mapping such thatC(x)is a closed pointed and convex cone withintC(x)∅for eachx∈X,the set-valued mappingM=Z{−intC(x)}be upper semicontinuous onX,T:X→be upper semicontinuous onXwith compact values,andη:X×X → Ebe affine in thefi rst argument withη(x,x)=0for allx∈X.For eachy∈X,assume that

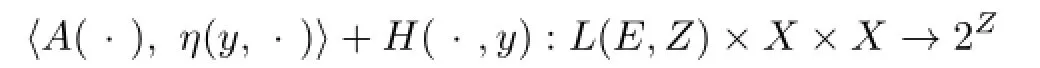
is an upper semicontinuous set-valued mapping with compact values.Suppose that there exists a mappingR:X×X→2Zsuch that

(i)for allx,y∈X,there exists ans∈T(x)such that

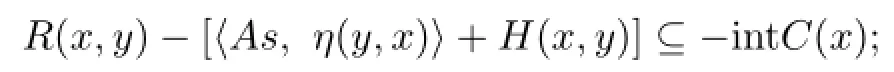
(ii)For any fi nite set{y1,y2,···,yn}⊆Xand==1, there is aj∈{1,2,···,n}such thatR(,yj)−intC();

(iii)For each sequenceinXwithxn∈Xnfor alln=1,2,···,which is escaping fromXrelative tothere exist anm∈Nand azm∈D(xm)∩Xmsuch that

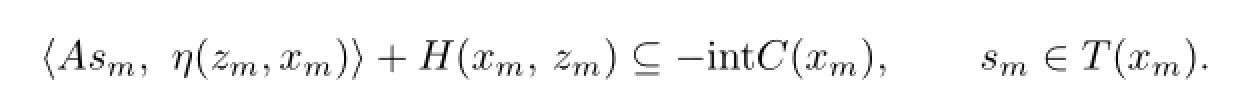
Then GVQVLIP has a solution.

Proof.De fi ne two set-valued mappings P:X→2X,P1:X→2Xby

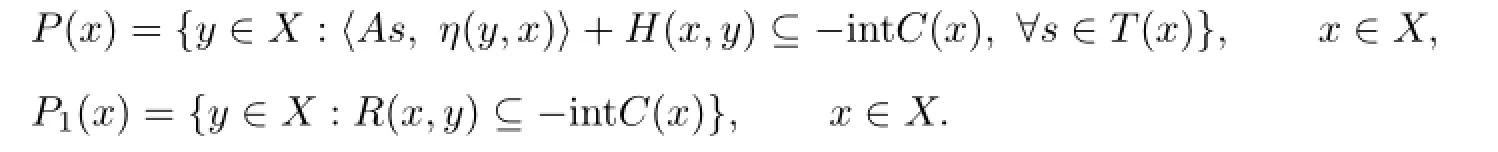
The condition(i)implies that P1(x)⊇P(x)for all x∈X.Hence,x̸∈co(P(x))for all x∈X.

The remainder of the proof is the same as of Theorem 3.1.

[1]Giannessi F.Theorem of Alternative,Quadratic Programs and Complementarity Problems.in: Cottle R W,Giannessi F,Lions J L.Variational Inequality and Compelementarity Problems. Chichester,UK:John Wiley and Sons,1980.

[2]Lee G M,Kim D S,Lee B S.Generalized vector variational inequality.Appl.Math.Lett.,1996,9:39–42.

[3]Yang X Q,Yao J C.Gap functions and existence of solutions to set-valued vector variational inequalities.J.Optim.Theory Appl.,2002,115:407–417.

[4]Chen G Y,Li S J.Existence of solutions of a generalized vector variational inequality.J. Optim.Theory Appl.,1996,90:321–324.

[5]Ding X P.The generalized vector quasi-variational-like inequalities.Comput.Math.Appl., 1999,37:57–67.

[6]Peng J W,Rong W D.Generalized vector quasi-variational-like inequalities without monotonicity and compactness.J.Math.Res.Exposition,2005,25:415–422.

[7]Ahmad R,Irfan S S.On generalized nonlinear variational-like inequalities problems.Appl. Math.Lett.,2006,19:294–297.

[8]Xiao G,Fan Z Q,Qi X G.Existence results for generalized nonlinear vector variational-like inequalities with set-valued mapping.Appl.Math.Lett.,2010,23:44–47.

[9]Schaefer H H.Topological Vector Spaces.Graduate Texts in Mathematics.vol.3.New York: Springer,1980.

[10]Ding X P,Tarafdar E.Generalized variational-like inequalities with pseudomonotone set-valued mappings.Arch.Math.(Basel),2000,74:302–313.

[11]Chiang Y,Chadli O,Yao J C.Generalized vector equilibrium problems with trifunctions.J. Global Optim.,2004,30:135–154.

[12]Liu Q M,Fan L Y,Wang G H.Generalized vector quasi-equilibrium problems with set-valued mappings.Appl.Math.Lett.,2008,21:946–950.

[13]Aubin J P,Ekeland I.Applied Nonlinear Analysis.New York:John Wiley and Sons,Inc., 1984.

[14]Su C H,Sehgal V M.Some fi xed point theorems for condensing multifunctions in locally convex spaces.Proc.Amer.Math.Soc.,1975,50:150–154.

[15]Tian G Q,Zhou J X.Quasi-variational inequalities without the concavity assumption.J.Math. Anal.Appl.,1993,172(1):289–299.

[16]Yuan G X,Isac Z G,Tan K K.The study of minimax inequalities,abstract economics and applications to variational inequalities and Nash equilibraia.Acta Appl.Math.,1998,54:135–166.

tion:49J40,54C60

A

1674-5647(2014)01-0090-07

Received date:Feb.7,2012.

Foundation item:The NSF(60804065)of China,the Foundation(11A029,11A028)of China West Normal University,the Fundamental Research Funds(13D016)of China West Normal University,the Key Project(211163) of Chinese Ministry of Education,and Sichuan Youth Science and Technology Foundation(2012JQ0032).

*Corresponding author.

E-mail address:gaodapeng126@126.com(Gao D P),cwnufsq@163.com(Feng S Q).