Stochastic Nonlinear Beam Equations with L´evy Jump

(College of Mathematics,Jilin University,Changchun,130012)

Stochastic Nonlinear Beam Equations with L´evy Jump

CHEN FENG

(College of Mathematics,Jilin University,Changchun,130012)

Communicated by Li Yong

In this paper,we study stochastic nonlinear beam equations with L´evy jump,and use Lyapunov functions to prove existence of global mild solutions and asymptotic stability of the zero solution.

stochastic extensible beam equation,L´evy jump,Lyapunov function, stability

1 Introduction

Consider a wide class of abstract stochastic beam equations with L´evy jump in a separable Hilbert space H:

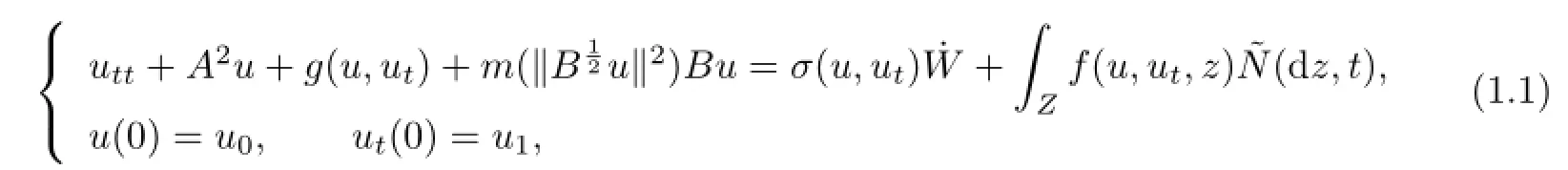
where A and B are positive self-adjoint operators,m is a nonnegative function in C1([0,+∞)), W is a Wiener process,and˜N is the compensated Poisson measure.

In[1],a model for the transversal de fl ection of an extensible beam of a natural length l was proposed as follows:

Chow and Menaldi[2]considered a stochastic extensible beam equation which describes large amplitude vibrations of an elastic panel excited by aerodynamic forces.They studieda stochastic beam equation as follows:

Brze´zniaket al.[3]studied(1.3),gave a wide class of abstract stochastic beam equations, proved nonexplosion of mild solutions to(1.3),and established the asymptotic stability of the zero solution when the damping term g is of the form

Recently,the stochastic partial di ff erential equations driven by jump processes have been studied by some scholars.Albeverioet al.[4]studied the stochastic reaction di ff usion equations driven by Poisson random measures,and established the existence and uniqueness of the solution under growth and Lipschitz conditions.Fournier[5]used Malliavin calculus to study the continuity of the law of the weak solution of the stochastic reaction di ff usion equations driven by Poisson random measures.Mueller[6]constructed a minimal solution for the stochastic heat equation driven by non-negative L´evy noise with coefficients of polynomial growth.Mytnik[7]established a weak solution for the stochastic partial equation driven by a one sided,α-stable noise without negative jumps.R¨ockner and Zhang[8]studied the stochastic evolution equations driven by both Brownian motion and Poisson point processes, and obtained the existence and uniqueness results of the equations.

The purpose of the present paper is to deal with the stochastic beam equations driven by white noise and Poisson noise.The model describes large amplitude vibrations and rare events with low frequency and sudden occurrence vibrations of an elastic panel excited by aerodynamic forces.We prove the existence of global solutions of the system(1.1),by using the technique of constructing a proper Lyapunov function(see[9]),i.e.,we assume that there exists a Lyapunov function V(u):H→R of the system(1.1)such that

and the coefficient of system(1.1)satis fi es some conditions,then there exists a global solution of the system(1.1)for all t≥t0.

The stability result in this paper depends on the form of g(u,ut).We can establish the asymptotic stability of zero solution when the damping term g is of the form

where h∈C1([0,∞))is a nonnegative function.

2 Notations and Preliminaries

Let H be a separable Hilbert space with the norm and the inner product denoted by‖·‖and〈·,·〉,respectively.Suppose that

(H2)W is a Wiener process in another real separable Hilbert space U with a covariance operator Q,and is de fi ned on a stochastic basissuch thatcontains all P-null sets.

(H3)Let p=(p(t)),t∈Dpbe a stationaryPoisson point process on a measure space (Z,Z,ν),where ν is a σ- fi nite measure,and N(dt,dx)be the Poisson counting measure associated with p,i.e.,

Let

be the compensated Poisson measure on[0,T]×Ω×Z.

(H4)m∈C1([0,∞))is a nonnegative function.

To interpret(1.1),we set

Then we set

Let X=(u,v)and X0=(u0,u1).Then(1.1)is rewritten as

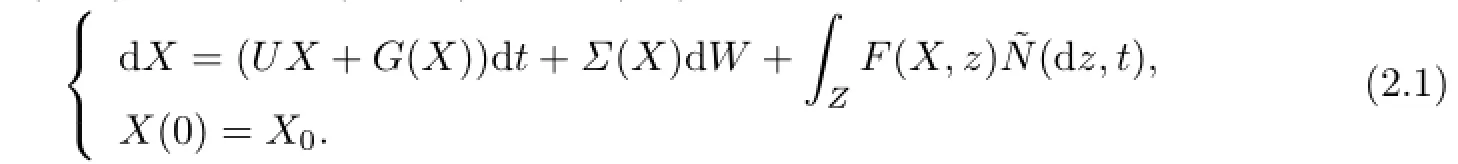
In order to obtain the existence and uniqueness of the mild solution to(1.1),we impose certain growth and global Lipschitz conditions on the coefficients g,σ and f of the system (1.1)in a Hilbert space.We introduce the subspace U0=with its natural Hilbert structure.Letbe the Hilbert-Schmidt operator space.

Suppose that

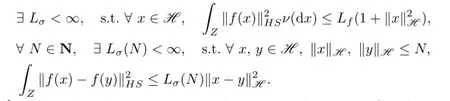
From[3]we know that the operators U and−U are m-dissipative,G and F are Lipschitz continuous,and there exist nonexplosion mild solutions of(2.1).We de fi ne the mild solution of(2.1)as follows:

Set

In order to show the stability of the zero solution,the damping term g of(1.1)is of the form g(u,ut)=βut+h(|u|2)u,β≥0,where h∈C1([0,∞))is a nonnegative function.In addition,assume that σ and f satisfy the linear growth conditions,respectively,as follows:

3 Existence of Global Solutions

We fi rst prove the existence of the stochastic beam di ff erential equations in fi nite dimension, and then we extend the results to the in fi nite dimension by the Galerkin method.De fi ne

Thus,there exists an orthomornal basisof H,which consists of eigenvectors of A,such that for k=1,2,···,

Then the Galerkin equations associated with(2.1)can be expressed as

Theorem 3.1Suppose that(H1)–(H5)are given above,andX0:Ω→(2.1)admits a unique global mild solutionXon[0,∞).The processX∈L∞([0,∞);is adapted and c`adl`ag.

De fi ne an energy functional onby

Lemma 3.1Under the assumptions in Theorem3.1,letThen thereexistλ＞0andC＞0such that

Proof.Applyingformula toΨ(X(n)(t)),we have

where DΨand D2Ψdenote the fi rst and the second Fr´echet derivatives of the functionalΨ,respectively,

and

From(3.4)-(3.5)we get

and

where

Taking expectation on both sides of(3.3),we have

From(3.8)we get

where

Proof of Theorem 3.1From Lemma 3.1 it follows thatis bounded in L∞(0,T;Then we choose a subsequence ofand denote it bysuch that

Now we check that X in(3.9)is a weak solution of(2.1).To attain this,we proceed the following steps:

(ii)We claim A2u(nk)⇀A2u in L2(0,T,V∗).Actually,for each η∈L2(0,T,V),

where λkand ekare the eigenvalues and the eigenvectors of the operator A2,respectively, so thatand

where

(v)We claim Pnσ(X(nk))˙W ⇀σ(X)˙W in L2(0,T,V∗).Actually,

Thus

According to(i)–(v),we take weak limit on both sides of(3.1)as n→∞and we fi nd that X(0,T;)is a solution of(2.1).This completes the proof.

4 Stability

In this section,we prove the stability of solutions to(1.1),which are given as follows:

Theorem 4.1Suppose that(H1)–(H5)are given above,

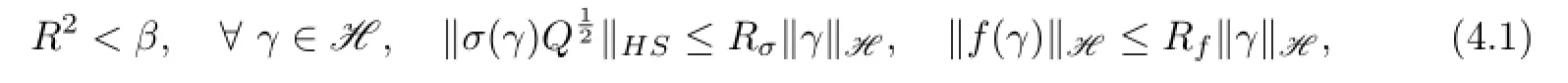
and there exists anα＞0such that

Then the zero solution of(1.1)is exponentially mean-square stable with probability one,i.e.,there exists constantsC＜∞,λ＞0such that ifXis a solution to(1.1)satisfying Φ(X0)＜∞,then we have

We de fi ne an operator P(see[3])by

that is,

The operator P is a positive,self-adjoint isomorphism of H,which has proved in[3]. So we can construct a Lyapunov functionΦ:H →R+by

Lemma 4.1Suppose that the hypotheses of Theorem1.1are satis fi ed.Then there exists a constantλ＞0such that ifXis a solution of(2.1)with Φ(X(0))＜∞,then the process(eλtΦ(X(t)))t≥0is a nonnegative continuous supermartingale.

Proof.Obviously,Φ∈C2(H),and we have the fi rst and the second Fr´echet derivatives of the functionΦ,respectively,as follows:for γ=(x,y)T,

Now,we compute the terms that would appear in the Itˆo formula forΦ(X(t)).By using (4.5),we have

By using(4.6),we can compute the second derivative

For the stochastic term,we have

For the jump di ff usion term,we have

Brze´zniaket al.[3]proved that X is a global strong solution to(2.1).As the Itˆo formula cannot be applied directly toΦ(X(t)),we consider the approximating strong solution Xnof(2.1).Let us consider the Yosida approximations Un(n≥1)to V:

and introduce the canonical projections

For n∈N,we consider

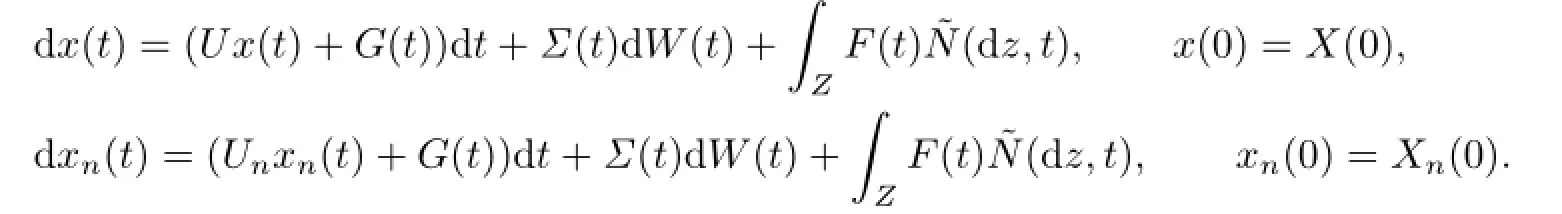
We have

By Fatou’s lemma,taking the limit as n→∞,we have

Let x(r)=X(r).We obtain

By(4.1)–(4.15),we have

Choosing k→∞,we have

This completes the proof.

Proof of Theorem 4.1In Lemma 4.1,we have proved that the process(eλtΦ(X(t)))t≥0is a nonnegative continuous supermartingale.We can directly prove our results from the proof of Theorem 1.4 in[3].By Lemma 4.1,we have

By using(4.4)and the nonnegativity of M,we obtain

This completes the proof.

[1]Woinowsky-Krieger S.The e ff ect of an axial force on the vibration of hinged bars.J.Appl. Mech.,1950,17:35–36.

[2]Chow P L,Menaldi J L.Stochastic PDE for nonlinear vibration of elastic panels.Di ff erential Integral Equations,1999,12:419–434.

[3]Brze´zniak Z,Maslowski B,Seidler J.Stochastic nonlinear beam equations.Probab.Theory Relat. Fields,2005,132:119–149.

[4]Albeverio S,Wu J L,Zhang T S.Parabolic SPDEs driven by Poisson white noise.Stochastic Process.Appl.,1998,74:21–36.

[5]Fournier N.Malliavin calculus for parabolic SPDEs with jumps.Stochastic Process.Appl.,2000,87:115–147.

[6]Mueller C.The heat equation with L´evy noise.Stochastic Process.Appl.,1998,74:67–82.

[7]Mytnik L.Stochastic partial di ff erential equations driven by stable noise.Probab.Theory Related Fields,2002,123:157–201.

[8]R¨ockner M,Zhang T.Stochastic evolution equations of jump type:existence,uniqueness and large deviation principles.Potential Anal.,2007,26:255–279.

[9]Khasminskii R Z.Stochastic Stability of Di ff erential Equations.Alphen:Sijtho ffand Noordho ff, 1980.

tion:60H15,60H40,60J75,35L70

A

1674-5647(2014)01-0023-10

Received date:March 25,2011.

Foundation item:The Graduate Innovation Fund(20101049)of Jilin University.

E-mail address:chenfengmath@163.com(Chen F).