Co fi niteness of Local Cohomology Modules with Respect to a Pair of Ideals

(Department of Mathematics,Soochow University,Suzhou,Jiangsu,215006)

Co fi niteness of Local Cohomology Modules with Respect to a Pair of Ideals

GU YAN

(Department of Mathematics,Soochow University,Suzhou,Jiangsu,215006)

Communicated by Du Xian-kun

Let R be a commutative Noetherian ring,I and J be two ideals of R,and M be an R-module.We study the co fi niteness and fi niteness of the local cohomology module(M)and give some conditions for the fi niteness of HomR(R/I,and(R/I,(M)).Also,we get some results on the attached primes of HdimMI,J(M).

local cohomology,co fi nite module,attached prime

1 Introduction

Throughout this paper,we always assume that R is a commutative Noetherian ring,I and J are two ideals of R,and M is an R-module.Takahashiet al.[1]introduced the concept of local cohomology module(M)with respect to a pair of ideals(I,J).The set of elements x of M such that In⊆Ann(x)+J for some integer n≫1 is said to be(I,J)-torsion submodule of M and is denoted byΓI,J(M).For an integer i≥0,the local cohomology functorwith respect to(I,J)is de fi ned to be the i-th right derived functor ofΓI,J.Note that,if J=0,thencoincides withWhen M is fi nitely generated,we know that(M)=0 for i＞dimM from Theorem 4.7 in[1].

Hartshorne[2]de fi ned an R-module M to be I-co fi nite if

is fi nitely generated for all i≥0.Also,he asked the following question:

QuestionIf M is fi nitely generated,when is ExtjR(R/I,HiI(M)) fi nitely generated forall i≥0 and j≥0(considering Supp((M))⊆V(I),so(R/I,(M))is fi nitely generated if and only ifis I-co fi nite).

Hartshorne[2]showed that if(R,m)is a complete regular local ring and M is fi nitely generated,thenis I-co fi nite in two cases:

(a)I is a non-zero principal ideal;

(b)I is a prime ideal with dimR/I=1.

Yoshida[3],Del fi no and Marley[4]extended(b)to all dimension one ideals I of any local ring R,and Kawasaki[5]proved(a)for any ring R.

Let

As a generalization of I-co fi nite module,we give the following de fi nition:

De fi nition 1.1AnR-moduleMis said to be(I,J)-co fi nite ifSuppM ⊆W(I,J)and(R/I,M)is fi nitely generated for alli≥0.

For an R-module M,the cohomological dimension of M with respect to I and J is de fi ned as

When J=0,then cd(I,J,M)coincides with cd(I,M).

In this paper,we mainly consider the(I,J)-co fi niteness ofSince

we focus on the fi niteness of(R/I,(M)).

In Section 2,we discuss the fi niteness of HomR(R/I,(M))(see Theorem 2.1),which generalizes Theorem 2.1 in[6]and Theorem B(β)in[7].In addition,when M is fi nitely generated and I is a principal ideal or cd(I,J,M)=1,we get the(I,J)-co fi niteness offor all i≥0,which generalizes the corresponding results in[5]and[9],respectively. In Proposition 2.3(iii)of[10],it is proved that if

then

In this paper,we get the corresponding result for the local cohomology module with respect to(I,J).In Section 3,we prove the(I,J)-co fi niteness ofwhich is a generalization of Theorem 3 in[4].

2 The Co fi niteness of(M)

First,we give a theorem which is a generalization of Theorem 2.1 in[6]and Theorem B(β) in[7].It is also a main result of this paper.

Theorem 2.1Assume thatMis anR-module,andsis a non-negative integer,such that(R/I,M)is fi nitely generated.If(M)is(I,J)-co fi nite for alli＜s,thenHomR(R/I,(M))is fi nitely generated.In particular,Ass((M))∩V(I)is a fi nite set.

Proof.We use induction on s.Let s=0.Then

This result is clear.Now we assume that s＞0,and the result has been proved for smaller values of s.Since(M)is(I,J)-co fi nite,(R/I,(M))is fi nitely generated for all i≥0.The short exact sequence

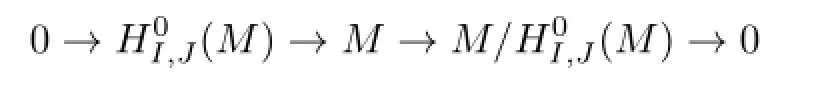
induces the exact sequence

It is easy to see that

So,we may assume that

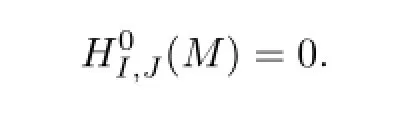
Then

Let E be an injective hull of M and put N=E/M.Then

From the short exact sequence

we have that

and

Applying the inductive hypothesis to N,it yields the fi niteness of HomR(R/I,(N)). Hence HomR(R/I,(M))is fi nitely generated.It follows that Ass((M))∩V(I)is a fi nite set.

Proposition 2.1Assume thatMis anR-module,andsis a non-negative integer,such that(R/I,M)is fi nitely generated.If(R/I,(M))is fi nitely generated for alli＜s,then(R/I,(M))is fi nitely generated.

Proof.We prove the result by induction on s.When s=0,from the short exact sequence

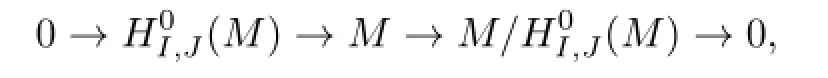
we get the exact sequence

Now we suppose that s＞0,and the claim has been proved for smaller values of s.From the exact sequence

Proposition 2.2Assume thatMis fi nitely generated,andsis a non-negative integer, such that(M)is Artinian for alli＜s.Then(M)is(I,J)-co fi nite for alli＜s.

Proof.We use induction on i.When i=0,since M is fi nitely generated,the result is clear. Now we suppose that i＞0,and the result has been proved for smaller values of i.By the inductive hypothesis,(M)is(I,J)-co fi nite for all j＜i.Hence,HomR(R/I,(M)) is fi nitely generated by Theorem 2.1,that is,0I is fi nitely generated,and thus

where I=(a1,a2,···,at)for all k≥0 by Theorem 5.1 in[8].By the same proof with Theorem 5.5 in[9],we deduce that

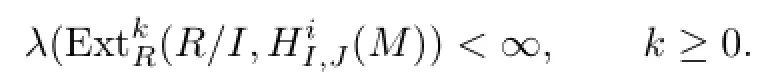
By Theorem 2.1 and Proposition 2.2,we have the following results.

Proposition 2.3Assume thatMis fi nitely generated,andsis a non-negative integer, such that(M)is Artinian for alli＜s.ThenHomR(R/I,(M))is fi nitely generated.In particular,Ass((M))∩V(I)is a fi nite set.

Proposition 2.4Assume thatMis anR-module,andsis a non-negative integer,such that(R/I,(M))is fi nitely generated for alliandj(respectively fori≤sand allj).Then(R/I,M)is fi nitely generated for alli(respectively fori≤s).

Proof.The case s=0 is clear.Now we suppose that s＞0 and the case s−1 is settled. Set N=M/(M).Then we have the long exact sequence

and

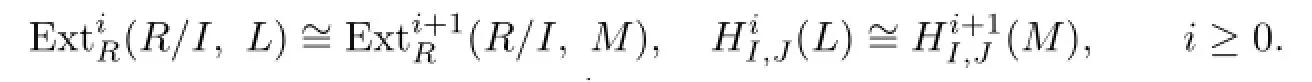
Furthermore,we get the fi niteness of(R/I,L)for all i(respectively for i≤s−1)by the inductive hypothesis.So(R/I,M)is fi nitely generated for all i(respectively for i≤s).The proof is completed.

Corollary 2.1Assume thatMis anR-module,andsis a non-negative integer,such that(M)is(I,J)-co fi nite for alli(respectively for alli≤s).Then(R/I,M)is fi nitely generated for alli(respectively for alli≤s).

Proposition 2.5Assume thatMis anR-module,sis a non-negative integer,such that(R/I,M)is fi nitely generated for alli≥0,and(M)is(I,J)-co fi nite for alli=s. Then(M)is(I,J)-co fi nite.

Proof.We prove the result by induction on s.Let N=M/(M).Then we have that

we get the following long exact sequence:

Now we assume that s＞0 and the claim holds for s−1.We see that(R/I,N)is fi nitely generated for all i≥0.By using the above long exact sequence and similar argument to that of Theorem 2.1 and letting L=E(M)/M,we can get

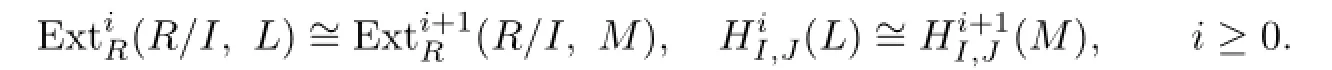
Corollary 2.2Assume thatMis a fi nitely generatedR-module,andcd(I,J,M)=1. Then(M)is(I,J)-co fi nite for alli≥0.

Proposition 2.6Assume thatMis a fi nitely generatedR-module,andIis a principal ideal.Then(M)is(I,J)-co fi nite for alli≥0.

Proof.Note that(M)=0 for all i＞ara(IR¯)by Proposition 4.11 in[1],where

So when I is a principal ideal,(M)=0 for all i＞1.Since(M)is fi nitely generated,(M)is(I,J)-co fi nite for all i=1.The result is clear.

Proposition 2.7Assume thatMis anR-module.Then we have

Proof.Let E be the injective hull of M/(M).Put N=E/(M/(M)).Since

we have

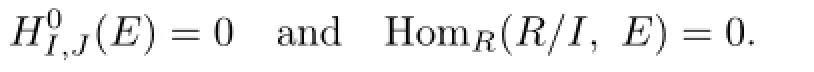
From the exact sequence

we have

and

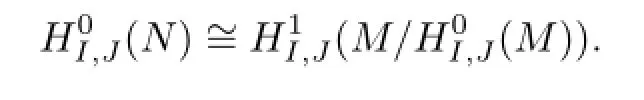
Hence

Next we give a proposition,which generalizes Proposition 2.3(iii)of[10].

Proposition 2.8Assume thatMis anR-module,andsis a positive integer such that

Then

Proof.When s=1,(M)=0.The result is clear,since

Suppose that s＞1 and the claim holds for s−1.Let E be an injective hull of M.Put N=E/M.Since(M)=0,we have(E)=0.By the exact sequence

we have

So

Thus

by the induction hypothesis.Hence

3 The Co fi niteness of(M)

In this section,we always assume that(R,m)is a commutative Noetherian local ring,I and J are two ideals of R,and M is an R-module.

Assume that M is fi nitely generated.We know that(M)is Artinian by Theorem 2.1 in[11].Next,we discuss Att(M))and the co fi niteness of(M).

Lemma 3.1[12]Suppose thatMis a non-zero fi nitely generatedR-module of dimensionn.Then

Next,we show the co fi niteness of(M).The following proposition is the key for this fact.

Proposition 3.1Assume thatRis a complete ring andMis a fi nitely generatedR-module of dimensionn.Then

Proof.Since(M)is Artinian,we have

Hence

by Theorem A in[13]and Lemma 3 in[4],therefore

Now the result is clear by Lemma 3.1.

Next,we give the main result of this section.

Theorem 3.1Assume thatMis a fi nitely generatedR-module of dimensionn.ThenHIn,J(M)is(I,J)-co fi nite.In fact,(R/I,(M))has fi nite length for alli≥0. Proof.Considering that(M)is Artinian,we know that(R/I,(M))is Artinian and

So we assume that R is complete.We know that D((M))is fi nitely generated and Att((M))is a fi nite set.Suppose that

Then

From Matlis Duality Theorem,we get

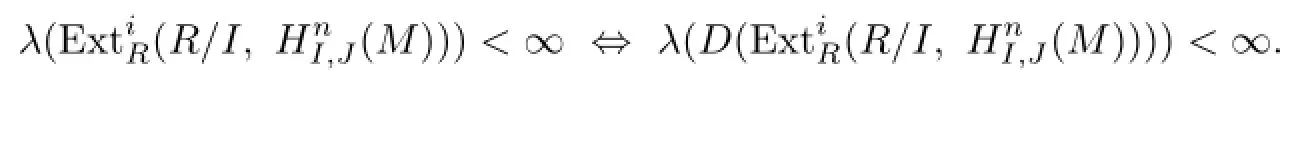
Since

by Theorem 11.57 in[14],it is enough for us to show that

In fact

by Proposition 3.1.

[1]Takahashi R,Yoshino Y,Yoshizawa T.Local cohomology based on a nonclosed support de fi ned by a pair of ideals.J.Pure Appl.Algebra,2009,213:582–600.

[2]Hartshorne R.Affine duality and co fi niteness.Invent.Math.,1970,9:145–164.

[3]Yoshida K I.Co fi niteness of local cohomology modules for ideals of dimension one.Nagoya Math.J.,1997,147:179–191.

[4]Del fi no D,Marley T.Co fi nite modules and local cohomology.J.Pure Appl.Algebra,1997, 121:45–52.

[5]Kawasaki K I.Co fi niteness of local cohomology modules for principal ideals.Bull.London Math.Soc.,1998,30:241–246.

[6]Dibaei M,Yassemi S.Associated primes and co fi niteness of local cohomology modules. Manuscripta Math.,2005,117:199–205.

[7]Khashyarmanesh K,Salarian S.On the associated primes of local cohomology modules.Comm. Algebra,1999,27:6191–6198.

[8]Melkersson L.Some applications of a criterion for artinianness of a module.J.Pure Appl. Algebra,1995,101:291–303.

[9]Melkersson L.Modules co fi nite with respect to an ideal.J.Algebra,2005,285:649–668.

[10]Hassanzadeh S H,Vahidi A.On vanishing and co fi niteness of generalized local cohomology modules.Comm.Algebra,2009,37:2290–2299.

[11]Chu L Z,Wang Q.Some results on local cohomology modules de fi ned by a pair of ideals.J. Math.Kyoto.Univ.,2009,49:193–200.

[12]Chu L Z.Top local cohomology modules with respect to a pair of ideals.Proc.Amer.Math. Soc.,2011,139:777–782.

[13]Dibaei M T,Yassemi S.Attached primes of the top local cohomology modules with respect to an ideal.Arch.Math.,2005,84:292–297.

[14]Rotman J.An Introduction to Homological Algebra.Orlando,FL:Academic Press,1979.

tion:13D45,13E15

A

1674-5647(2014)01-0033-08

Received date:April 15,2011.

Foundation item:The NSF(BK2011276)of Jiangsu Province,the NSF(10KJB110007,11KJB110011)for Colleges and Universities in Jiangsu Province and the Research Foundation(Q3107803)of Pre-research Project of Soochow University.

E-mail address:guyan@suda.edu.cn(Gu Y).