T∗-extension of Lie Supertriple Systems

(Academy of Mathematical and Computer Sciences,Hebei University,Baoding, Hebei,071002)

T∗-extension of Lie Supertriple Systems

FENG JIAN-QIANG

(Academy of Mathematical and Computer Sciences,Hebei University,Baoding, Hebei,071002)

Communicated by Du Xian-kun

In this article,we study the Lie supertriple system(LSTS)T over a fi eld K admitting a nondegenerate invariant supersymmetric bilinear form(call such a T metrisable).We give the de fi nition of T∗ω-extension of an LSTS T,prove a necessary and sufficient condition for a metrised LSTS(T,ϕ)to be isometric to a T∗-extension of some LSTS,and determine when two T∗-extensions of an LSTS are“same”,i.e., they are equivalent or isometrically equivalent.

pseudo-metrised Lie supertriple system,metrised Lie supertriple system,T∗-extension

1 Introduction

A Lie(super)triple system over a fi eld K is called pseudo-metrisable if it admits an invariant nondegenerate bilinear form,and if further,the bilinear form can be chosen to be (super)symmetric,then T is called metrisable.Recently,metrisable Lie(super)triple systems have attracted a lot of attention due to its applications in the areas of mathematics and physics(see,for example,[1–6]).

The method of T∗-extension of Lie algebras was fi rst introduced by Bordemann[7]in 1997 and this method is an important method for studying algebraic structures.In our early paper,we investigated the T∗-extension of Lie triple systems(see[6]).This paper is devoted to transfer the T∗-extension method to Lie supertriple systems.

Throughout this paper,all Lie supertriple systems considered are assumed to be of fi nite dimension over a fi eld K.

2 Lie Supertriple Systems

In this section,we fi rst brie fl y sketch the notion of a(pseudo-)metrisable Lie supertriple system.

Let V=V¯0⊕V¯1be aZ2-graded space over K,where V¯0and V¯1are called bosonic and fermionic space,respectively,in physics literature.We denote the degree by

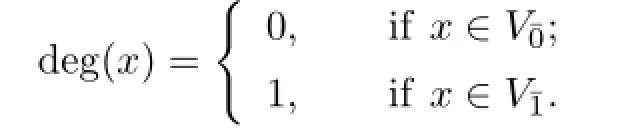
and write(−1)xy:=(−1)deg(x)deg(y).

Any element considered in this article is always assumed to be homogeneous,i.e.,either x∈V¯0or x∈V¯1.

Notice that the associate algebra EndV is a superalgebra EndV=End¯0V⊕End¯1V,

De fi nition 2.1A Lie supertriple system(LSTS)is aZ2-graded spaceT=T¯0⊕T¯1overKwith a trilinear composition[·,·,·],satisfying the following conditions:

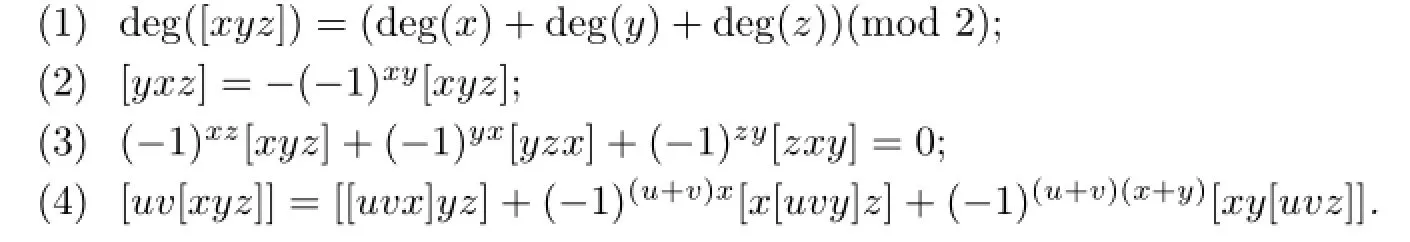
An ideal of an LSTS T is a graded subspace I for which[I,T,T]⊆I.Moreover,if [TII]=0,then I is called an abelian ideal of T.T is called abelian if it is an abelian ideal of itself.For any graded subspace V in T,the centralizer ZT(V)of V in T is de fi ned by

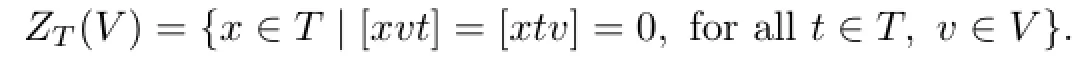
In particular,ZT(T)is called the center of T and denoted simply by Z(T).If T is an LSTS, de fi ne the lower central series for T by T0:=T and Tn+1:=[TnTT]for n≥0.T is called nilpotent(of nilindex m)if there is a(smallest)positive integer m such that Tm=0.Put T(0):=T and T(n+1):=[T(n)TT(n)].Then T is called solvable(of length k)if there is a (smallest)positive integer k such that T(k)=0.

De fi nition 2.2If an LSTSTadmits a nondegenerate bilinear formbsatisfying conditions

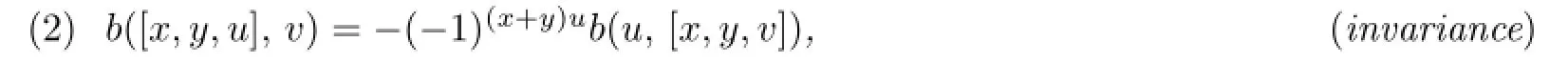
then we callTpseudo-metrisable and the pair(T,b)a pseudo-metrised LSTS.If,in addition,bsatis fi es also;

then we callTmetrisable and the pair(T,b)a metrised LSTS.

Proposition 2.1[1]The following conditions are equivalent:

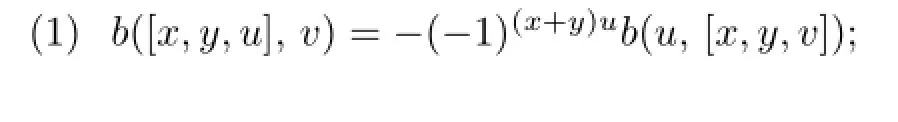
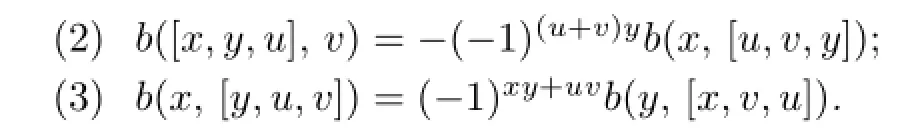
De fi ne multiplication operators L(·,·),P(·,·),R(·,·)on T by

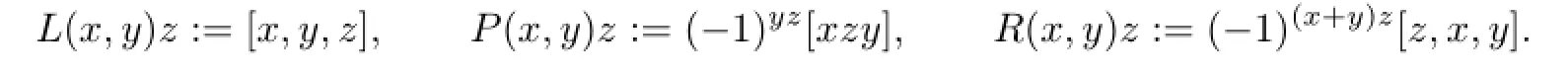
De fi nition 2.3Forx,y,z∈T,f∈T∗,de fi ne the following dual multiplication operators onT∗by

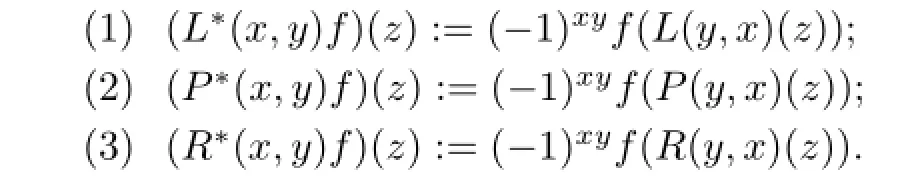
Noticing that for any x,y,z∈T,f∈T∗,

and

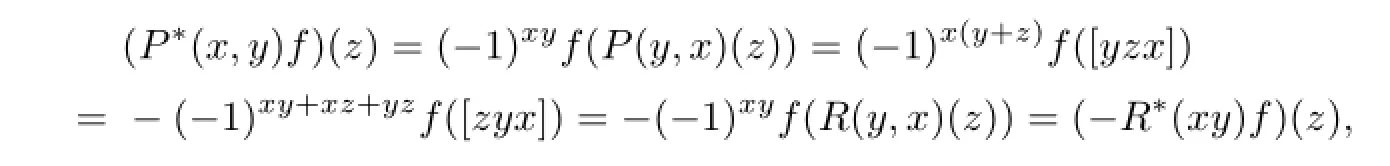
we have

De fi nition 2.4A trilinear mappingω:T×T×T→T∗is called a3-supercocycle if it satis fi es the following conditions:

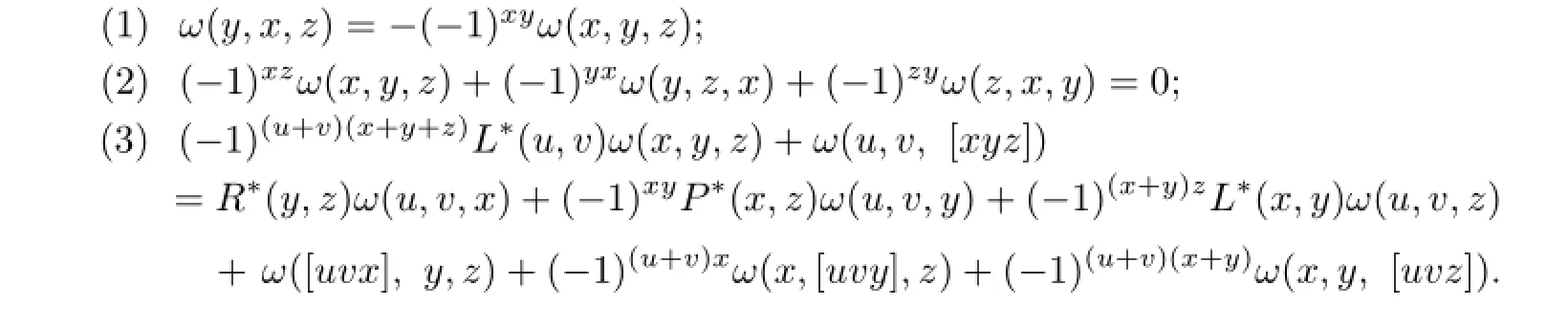
Lemma 3.1Let(T,ϕ)be a pseudo-metrised LSTS over a fi eldK,andVbe an arbitrary vector subspace ofT.

(i)LetIbe an ideal ofT.Then⊥IandI⊥are ideals ofTandI⊥,⊥I⊂ZT(I);

(ii)For arbitrary subspaceV,ZT(V)=[V TT]⊥=⊥[V TT].IfVis an ideal,thenZT(V)is an ideal;

(iii)In particular,Z(T)=(T(1))⊥=⊥(T(1))forT(1)=[TTT].

Now we consider the transfer of invariant bilinear forms from one LSTS to another.Let T(resp.T′)be an LSTS over a fi eld K,f(resp.g)be an invariant bilinear form on T(resp. T′),and m:T→T′be a homomorphism of LSTS.Then we have the following lemma.

Lemma 3.2Under the above assumptions,we have

(i)The pull backm∗gofgis again an invariant bilinear form onT;

(ii)Suppose thatmis surjective andkermis contained in the kernel off.Then the projectionfmoffis an invariant bilinear form onT′;

(iii)IfUis a subsystem ofT,thenU∩U⊥is an ideal ofU.Letp:U→U/(U∩U⊥)be the projection andfUbe the restriction offtoU×U.Then the projection(fU)pis a nondegenerate invariant bilinear form on the factor systemU/(U∩U⊥);

(iv)The bilinear formf⊥gis invariant on the direct sumT⊕T′.Moreover,f⊥gis nondegenerate if and only iffandgare nondegenerate.

The proofs of both Lemmas 3.1 and 3.2 are similar to that of Lie triple systems,which can be found in[6].

Now we generalize the notion of T∗-extension of a Lie triple system to that of a Lie supertriple system.

De fi nition 3.1LetTbe an LSTS,T∗be the dual space ofT,andωbe a3-supercocycle. De fi ne a ternary multiplication onT∗ωT=T⊕T∗by

for allx,y,z∈T,andf,g,h∈T∗,wherex+f(resp.y+g,z+h)is homogeneous of degreedeg(x)(resp.deg(y),deg(z)),and[xyz]Tis the Lie superbracket inT.

Lemma 3.3Under the above de fi nition,ifdeg(ω)=0,thenT∗ωTis an LSTS,which is called theT∗-extension of the LSTSTby means ofω.In particular,ifω=0,thenT∗0Tis called the trivialT∗-extension ofT.

Proof.Here we only consider the last equation in the de fi nition of LSTS.We need to verify

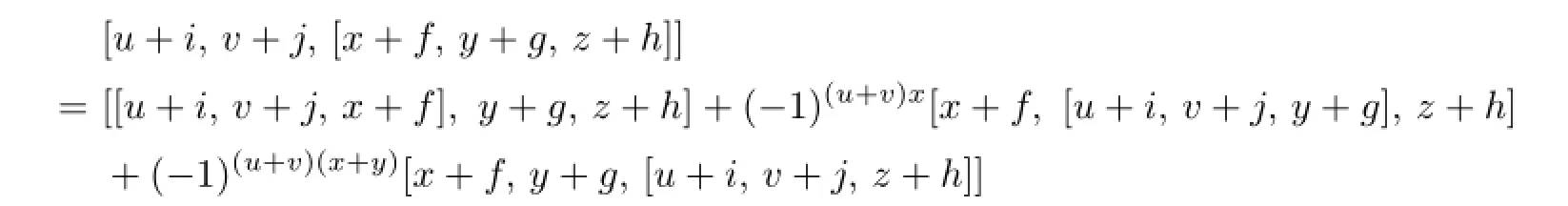
for u,v,x,y,z∈T,i,j,f,g,h∈T∗.Expand this equation by De fi nition 3.1.Then all items consist of the ternary compositions in T and the 3-supercocycle ω are canceled by the de fi nitions of an LSTS and a 3-supercocycle.The items consisting of h reads

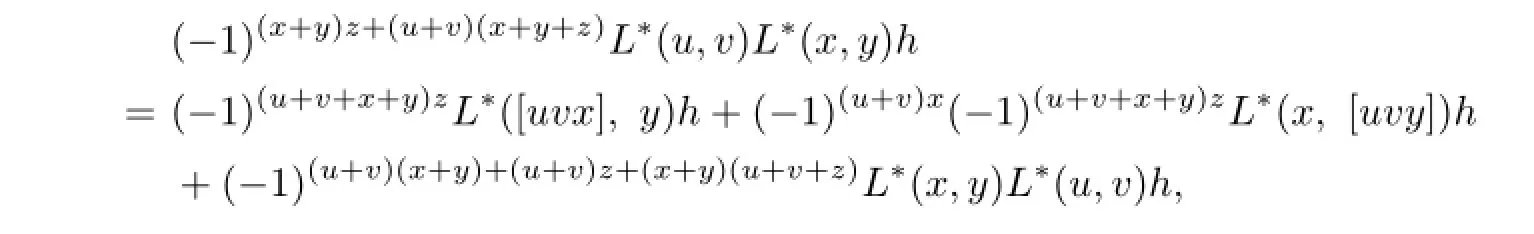
that is,

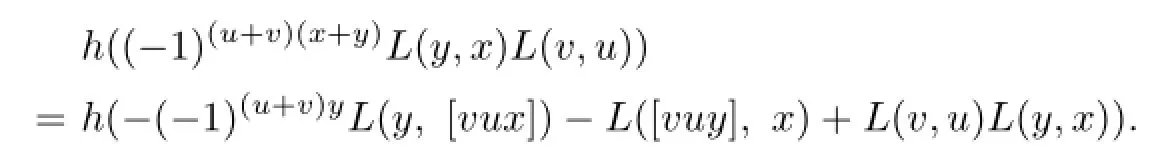
The above equation holds due to the last equation in the de fi nition of an LSTS.Other items consisting of i,j,f or g can be veri fi ed similarly.This completes the proof.

By this lemma,we always suppose that the 3-supercocycle ω satis fi es deg(ω)=0.

It is clear from the de fi nition that the subspace T∗is an abelian ideal of T∗ωT and T is isomorphic to the factor supertriple system T∗ωT/T∗.Moreover,consider the following consistent supersymmetric bilinear form qTon T∗ωT de fi ned for all x,y∈T,f,g∈T∗by

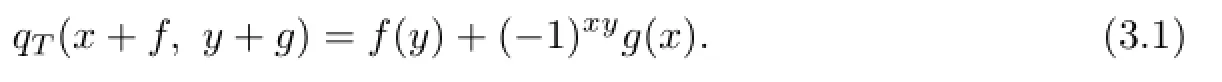
We then have the following lemma.

Lemma 3.4LetT,T∗,ωandqTbe as above.ThenqTis a nondegenerate supersymmetric bilinear form onand the following conditions are equivalent:

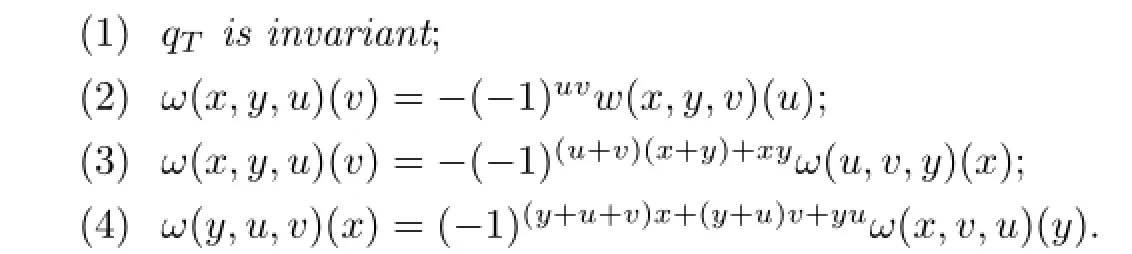
Hence(,qT)is a metrised LSTS if and only ifωsatis fi es one of(2)–(4).

Proof.If x+f is orthogonal to all elements ofthen,in particular,f(y)=0 for all y∈T and g(x)=0 for all g∈T∗,which implies that f=0 and x=0.So the supersymmetric bilinear form qTis nondegenerate.

Now we consider the invariant property.Let x,y,u,v∈T and f,g,p,q∈T∗.Then we have

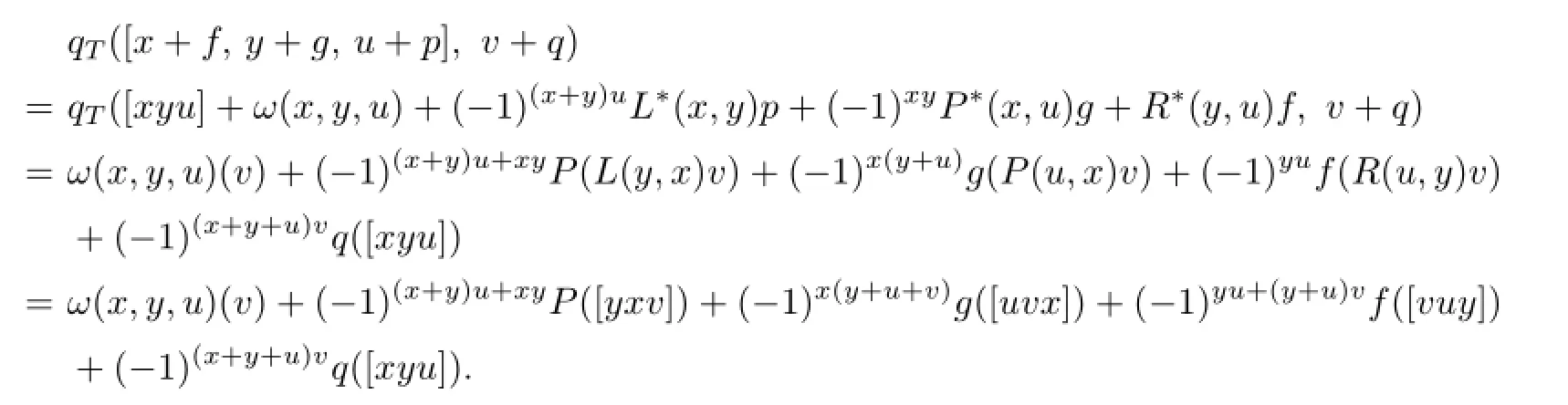
On the other hand,

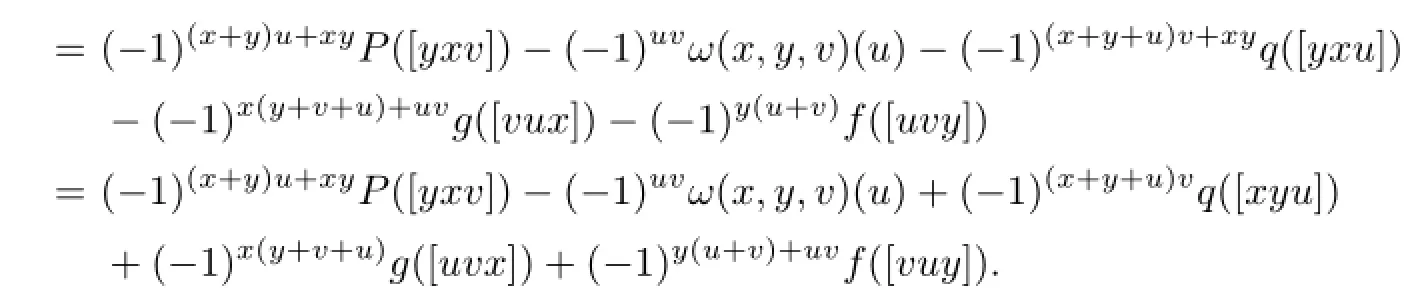
Comparing these results we get that qTis invariant if and only if

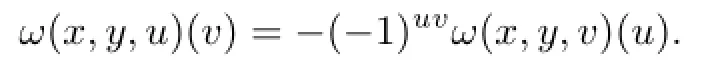
In a similar way,by the equivalence condition of Proposition 2.1,we can obtain also that qTis invariant if and only if

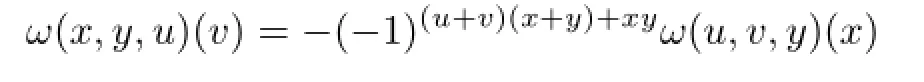
and if and only if

Thus the lemma is proved.

4 Metrisable LSTS

Lemma 4.1Let(T,ϕ)be a metrised LSTS of dimensionnover a fi eldK,andIbe anisotropicdimensional subspace ofT.ThenIis an ideal ofTif and only ifIsatis fi esI(1):=[TII]=0.HenceIis an ideal if and only ifIis an abelian ideal ofT.

Proof.Since dimI+dimI⊥=n it follows that I=I⊥.If I is an ideal of T,then

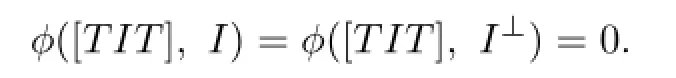
Hence ϕ(T,[TII])=0,and the non-degeneracy property of ϕ implies I(1)=[TII]=0. Conversely,if I(1)=[TII]=0,then

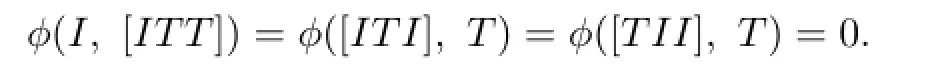
Hence[ITT]⊂I⊥=I.This implies that I is an ideal of T.

Theorem 4.1Let(T,ϕ)be a metrised LSTS of dimensionnover a fi eldKof characteristic not equal to two.Then(T,ϕ)is isometric to aT∗-extensionand onlyifnis even andTcontains an isotropic idealI(i.e.,I⊂ I⊥)of dimensionIn thiscase:B～=T/I.

Proof.Sufficiency.Since dimB=dimB∗,it is clear thatis even.Moreover,it is clear from the de fi nition of the multiplication in De fi nition 3.1 that B∗is an isotropic ideal of half the dimension of

Necessity.Suppose that I is an-dimensional isotropic ideal of T.Let B denote the factor supertriple system T/I and p:T→ B the canonical projection.Now,since the characteristic K is not equal to 2,we can choose an isotropic complementary vector subspace B0to I in T,i.e.,T=B0⊕I and=B0.Denote by p0(resp.p1)the projection T→B0(resp.T→I)along I(resp.along B0).Moreover,let ϕIdenote the linear map I→B∗:i→(px→ϕ(i,x)).It is well-de fi ned because ϕ(I,I)=0.Since ϕ isnondegenerate,I⊥=I,and dimIdimB.It follows that ϕIis a linear isomorphism.

Furthermore,ϕIhas the following intertwining property:Let x,y,z∈T and i∈I.Then

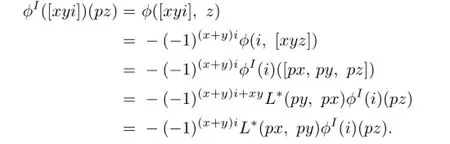
Hence after a completely analogous computation one has the following

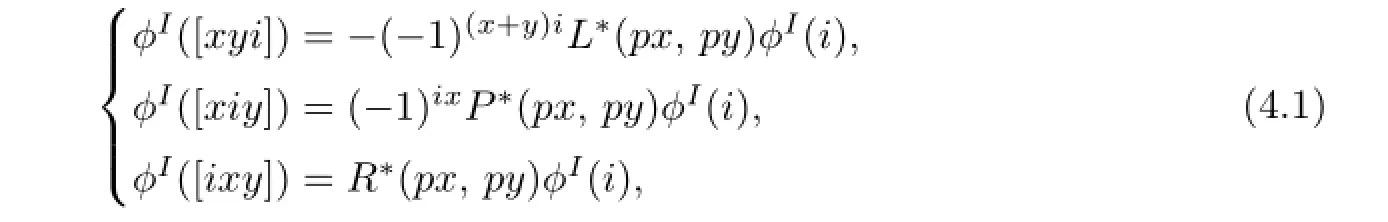
where x,y∈T and i∈I.We de fi ne the following trilinear map:

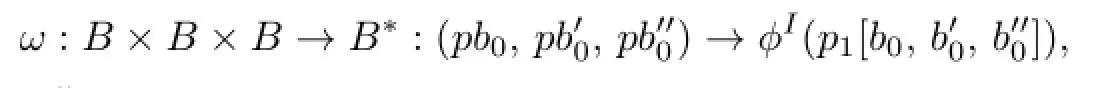
where b0,andare in B0.This is well-de fi ned since the restriction of the projection p to B0is a linear isomorphism.Now,let m denote the following linear map

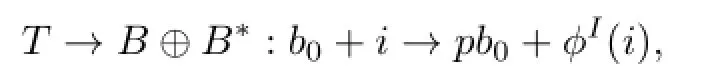
where b0∈B and i∈I.Since p is restricted to B0and ϕIare linear isomorphisms,the map m is also a linear isomorphism.Moreover,m is an isomorphism of the metrised LSTS(T,ϕ) to the T∗-extensionIndeed,letB and i,Then

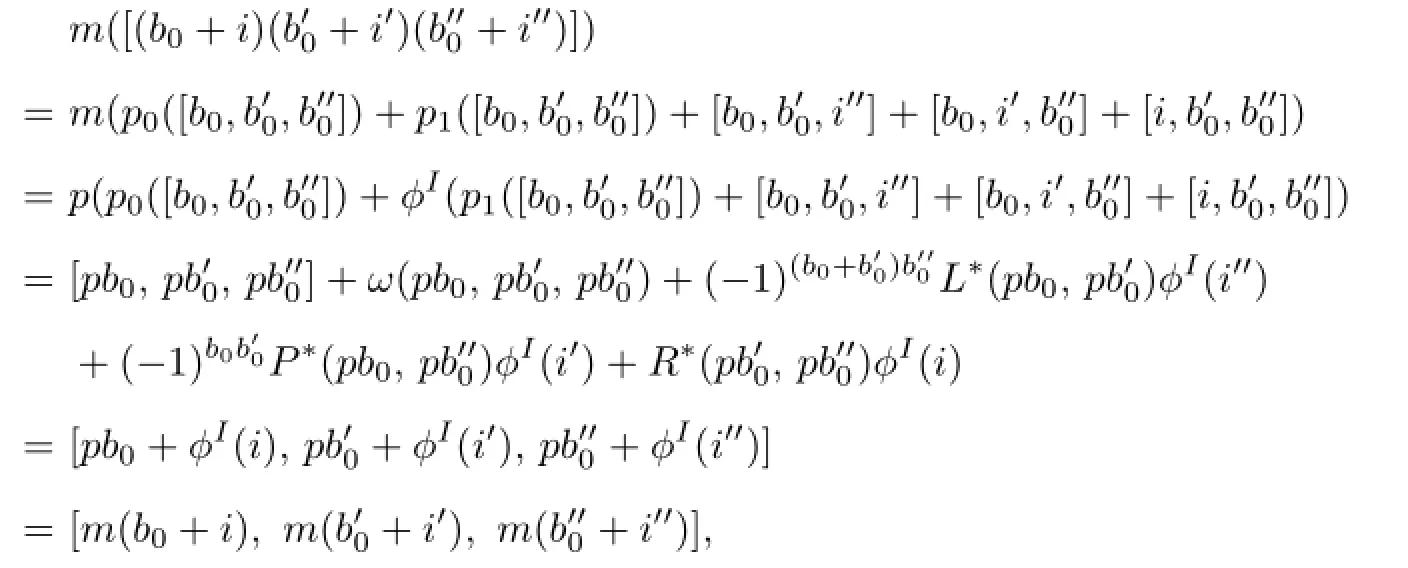
where we use the de fi nition of ω,the intertwining properties of ϕI,the fact that p is a homomorphism,the de fi nition of the product inlemma 4.1 and(4.1).In addition,we have

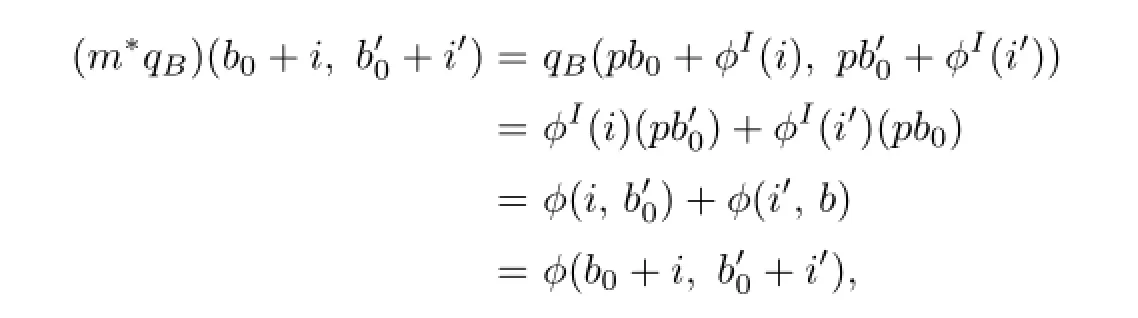
where the fact that B0could be chosen to be isotropic entered in the last equation.Hence,=ϕ which implies that qBis an invariant symmetric bilinear form onor thatω is cyclic.Therefore,(T,ϕ)andare isomorphic as metrised algebras and the theorem is proved.

The proof of this theorem shows that the trilinear map ω depends on the choice of the isotropic subspace B0of T complementary to the ideal I.Therefore,there may be di ff erent T∗-extensions describing the“same”metrised LSTS.

De fi nition 4.1LetBi,i=1,2,be two LSTS’s over a fi eldKandωi:Bi×Bi×Bi→i=1,2be two di ff erent3-supercocycles.TheT∗-extensionBiofBiare said to be equivalent ifB1=B2=Band there exists an isomorphism of LSTS Φ:B1→B2which is the identity on the idealB∗and which induces the identity on the factor LSTSB1/B∗=B=B2/B∗.The twoT∗-extensionsare said to be isometrically equivalent if they are equivalent and Φ is an isometry.

Theorem 4.2LetBbe an LSTS over a fi eld of characteristic not equal to2,and furthermore,letωi,i=1,2be two3-supercocycles:B×B×B→B∗.

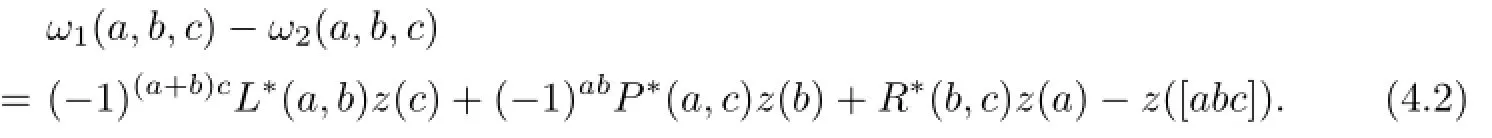
If this is the case,then the supersymmetric partzsofzwhich is de fi ned by

induces a symmetric invariant bilinear form onB,i.e.,

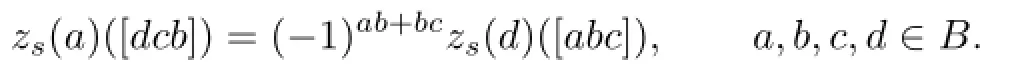
Proof.(i)The equivalence betweenB1andB2holds if and only if there is a homomorphism of LSTS

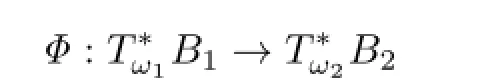
satisfying

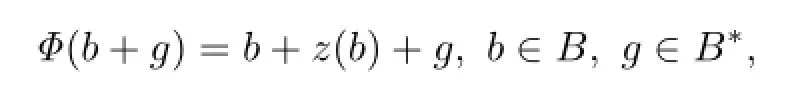
where z is the component ofΦthat maps B to B∗.Indeed,by the de fi nition,Φmust be the identity on B∗and we must have

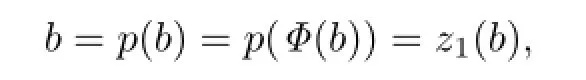
where z1(b)is the component ofΦthat maps B to B.Clearly,Φis a linear isomorphism for arbitrary z.Then for all a,b,c∈B and f,g,h∈B∗,we have

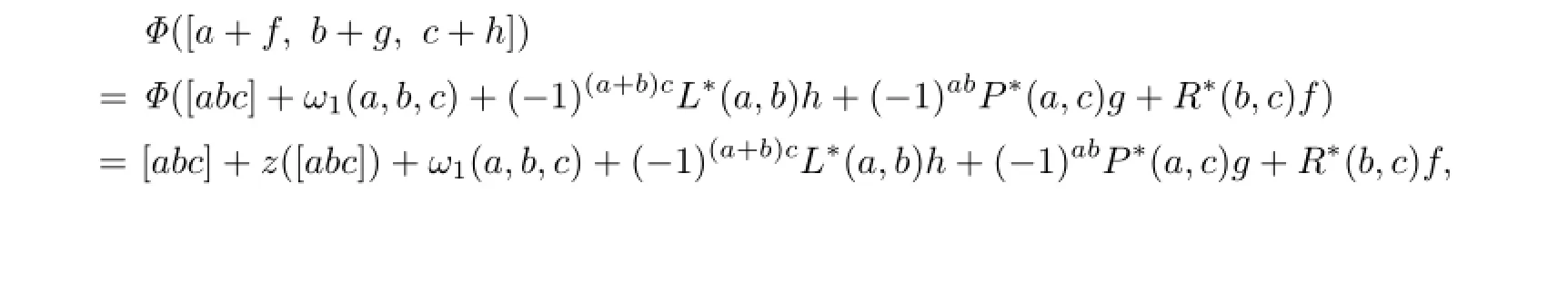
where the multiplication is formed inOn the other hand,

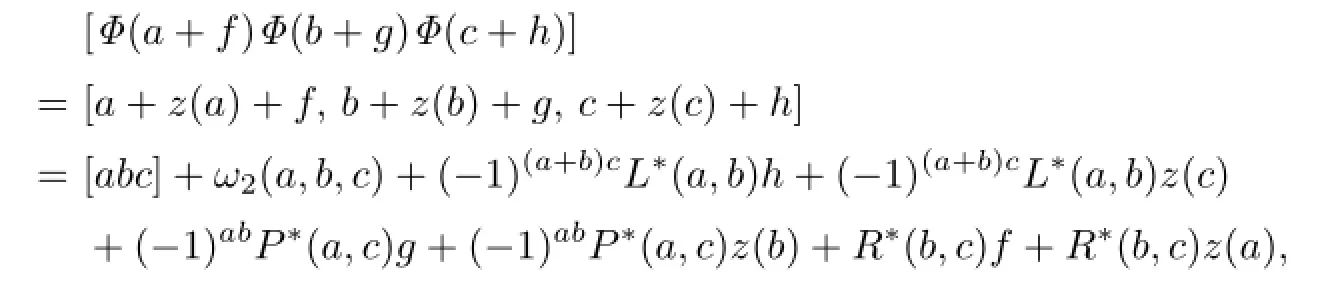
where the multiplication is formed inHenceΦis a homomorphism of LSTS if and only if(4.2)holds.Now split z into its anti-supersymmetric part zade fi ned by

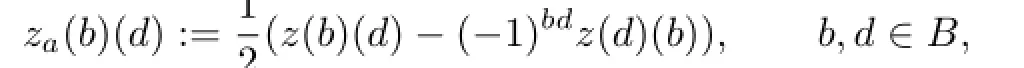
and its supersymmetric part zsde fi ned above.Then z=zs+za.We see that the right hand side of(4.2)evaluated on d∈B has the following form:

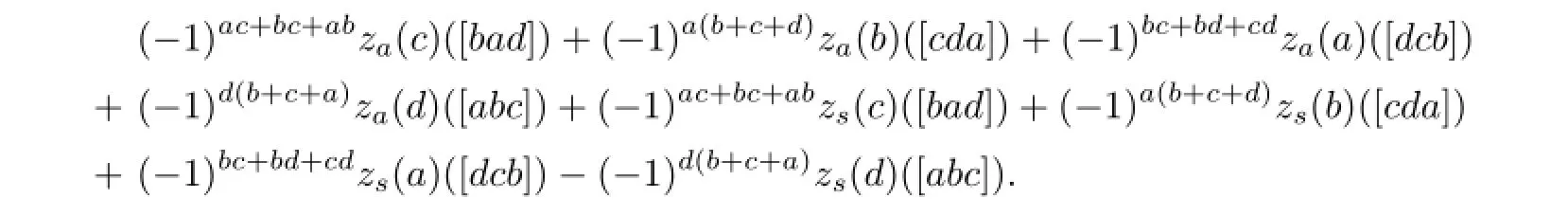
Writing the above summation as s(abcd)and considering

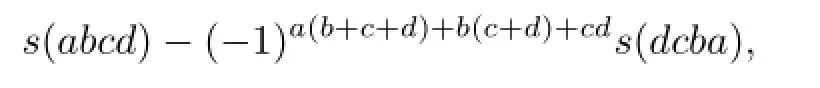
by Lemma 3.4(4),we get

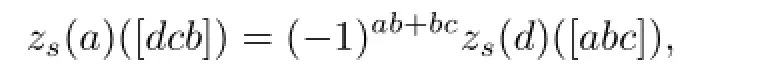
which proves the invariance of the supersymmetric bilinear form induced by zs.

(ii)Let the isomorphismΦbe de fi ned as in(i).Then,we have for all b,d∈B and f,g∈B∗

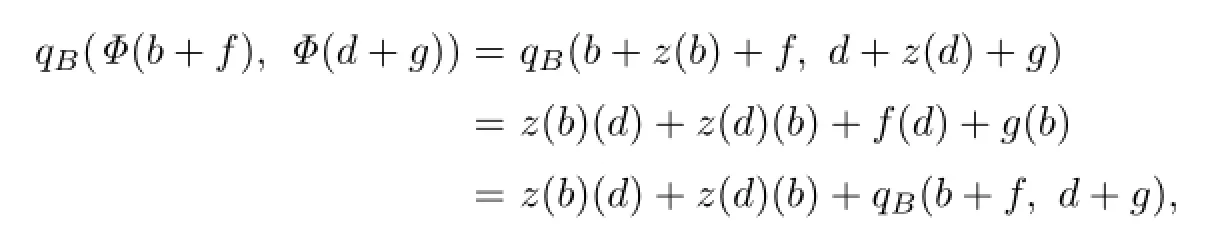
from which it is clear that ϕ is an isometry if and only if zs=0.

[1]Okubo S,Kamiya N.Quasiclassical Lie superalgebras and Lie supertriple systems.Comm. Algebra,2002,30:3825–3850.

[2]Okubo S,Kamiya N.Jordan-Lie superalgebra and Jordan-Lie triple system.J.Algebra,1997,198:388–411.

[3]Okubo S.Parastatistic as Lie supertriple systems.J.Math.Phys.,1994,35:2785–2803.

[4]Zhang Z X,Shi Y Q,Zhao L N.Invariant symmetric bilinear forms on Lie triple system.Comm. Algebra,2002,30(11):5563–5573.

[5]Zhang Z X,Li H J,Dong L.Invariant bilinear forms on anti-Lie triple systems.Chinese J. Contemp.Math.,2004,25:237–244.

[6]Feng J Q.Metrisable Lie triple systems.Acta Math.Sinica,2008,51(3):457–468.

[7]Bordemann B.Nondegenerate invariant bilinear forms on nonassociative algebras.Acta.Math. Univ.Comenian.,1997,LXVI(2):151–201.

tion:17A40,17B05

A

1674-5647(2014)01-0051-09

Received date:May 18,2011.

Foundation item:The NSF(A2010000194)of Hebei Province.

E-mail address:vonjacky@126.com(Feng J Q).