Variational Approach to Scattering by Inhomogeneous Layers Above Rough Surfaces

(1.College of Mathematics,Jilin University,Changchun,130012)

(2.College of Mathematics,Beihua University,Jilin City,Jilin,132013)

Variational Approach to Scattering by Inhomogeneous Layers Above Rough Surfaces

LUAN TIAN1,2AND MA FU-MING1

(1.College of Mathematics,Jilin University,Changchun,130012)

(2.College of Mathematics,Beihua University,Jilin City,Jilin,132013)

In this paper,we study,via variational methods,the problem of scattering of time harmonic acoustic waves by unbounded inhomogeneous layers above a sound soft rough surface.We fi rst propose a variational formulation and exploit it as a theoretical tool to prove the well-posedness of this problem when the media is nonabsorbing for arbitrary wave number and obtain an estimate about the solution,which exhibit explicitly dependence of bound on the wave number and on the geometry of the domain.Then,based on the non-absorbing results,we show that the variational problem remains uniquely solvable when the layer is absorbing by means of a priori estimate of the solution.Finally,we consider the fi nite element approximation of the problem and give an error estimate.

Helmholtz equation,rough surface,scattering problem

1 Introduction

This paper is concerned with the study of a boundary value problem for the Helmholtz equation modeling scattering of time harmonic waves by a layer above an unbounded rough surface on which the fi eld vanishes.Such problems arise frequently in practical applications, such as in modeling outdoor noise propagation or sonar measurements in oceanography.

In this paper we focus on a particular,typical problem of the class,which models acoustic waves scattering by inhomogeneous layer above a sound soft unbounded rough surface.Since the unboundedness of the scattering object present a major challenge,mathematical methods to solve such scattering problem are often difficult to develop.Nevertheless,a variety of di ff erent methods and techniques have been introduced during the last years.Most of them were concerned with Drichlet boundary value problems for the Helmholtz equation withconstant real wave number(see[1–7]).

The idea of our argument is inspired by[5–6],in which a Rellich identity was used to prove the estimates for solutions of the Helmholtz equation posed on unbounded domains. Though the results and methods were closest to those of Chandler[5,7],who studied the similar problem tackled in those papers,and considered the homogeneous media only for non-absorbing case in[5],and obtained the well posed results just only for the wave number which is small enough in[7].

The main results of this paper are as follows:In Section 2,we introduce the boundary value problem considered in this paper.Then we propose the variational formulation,which is used as a theoretical tool to analyze the well-posedness of the problem.In Section 3, we consider the non-absorbing case.We fi rst establish a Rellich-type identity,from which the inf-sup condition of the sesquilinear form follows.Then the existence and uniqueness of the solution to variational problem can be deduced by application of the generalized Lax-Milgram theory of Babuska(see[8]).In Section 4,we turn our interest to the absorbing scatterers,and establish the uniqueness via a priori estimate which also leads to an existence result based on the non-absorbing results.In Section 5,the fi nite element approximation of the problem is considered.Finally,we analyze the convergence and error estimate.

2 Boundary Value Problem and Variational Formulation

In this section,we fi rst de fi ne some notations related to the problem.Then we introduce the boundary value problem and its equivalent variational formulation to be analyzed later. For x=(x1,x2,···,xn)∈Rn(n=2,3),let˜x=(x1,x2,···,xn−1)so that x=(˜x,xn).For H∈R,let UH:={x|xn＞H}andΓH:={x|xn=H}.Suppose that D is a connected open set with some constants f−＜f+.Then it holds that

and

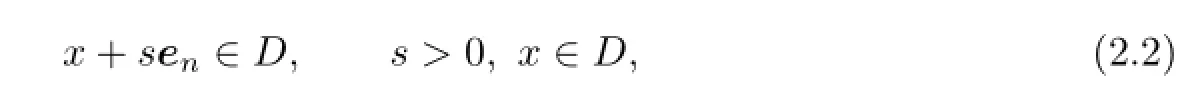
where endenotes the unit vector in the direction of xn.LetΓ=∂D and SH:=DUHfor some H≥f+.Moreover,we assume that the wave number k satis fi es

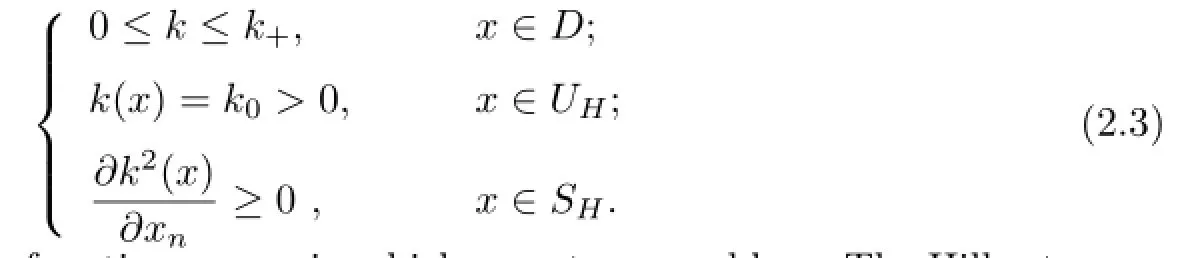
Next we introduce the main function spaces in which we set our problem.The Hilbert space VHis de fi ned by

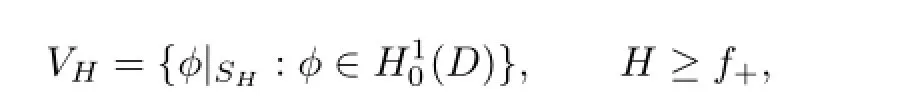
on which we impose the wave number dependent scalar product

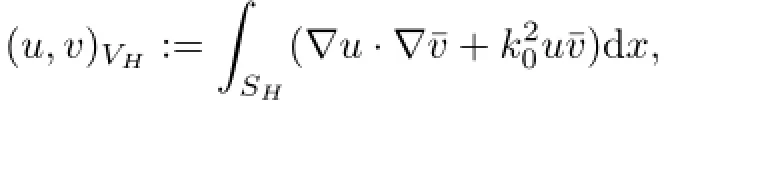
and the induced norm

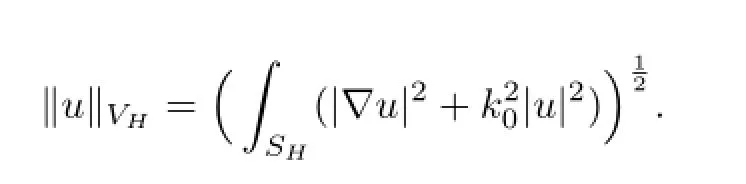
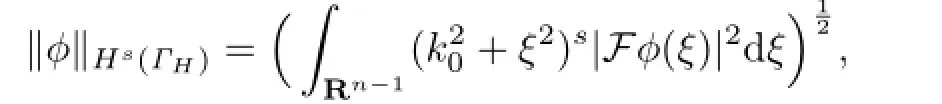
For s∈R,denote by Hs(ΓH)the usual Sobolev space(see[9])with norm where we identifyΓHwithRn−1and F is the Fourier transformation.

Then the problem of scattering by an inhomogeneous layer above a sound soft rough surface is formulated by the following boundary value problem:given a source g∈L2(D) supported in SHfor some H ≥f+,we seek to fi nd a scattered fi eld u:D→Csuch that∈Vafor every a＞f+,and

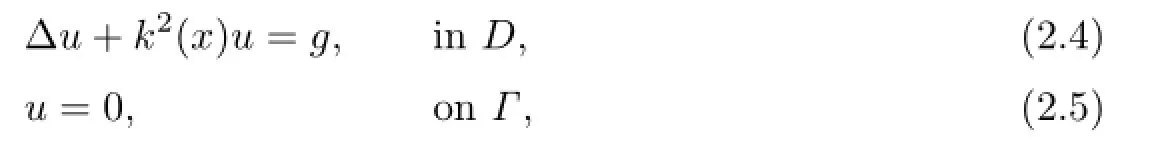
in a distributional sense.As part of the boundary value problem,we apply the radiation condition,which is often used in a formal manner in the rough surface scattering literature,

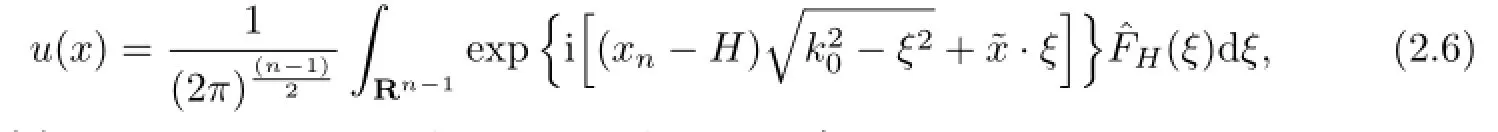
Before giving the variational formulation related to the above problem,we introduce some operators.Recall from[9]that,for all a＞H≥f+,there exist continuous embeddings,i.e., trace operators

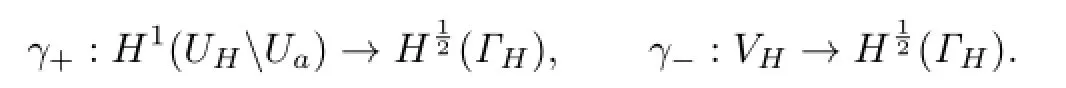
The Dirichlet to Neumann map T onΓHis de fi ned by

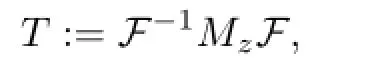
where Mzis the multiplying by

From the de fi nition of T and the Sobolev norm,we see that it is a map fromtoandNext we recall some results needed about properties of the above operators.

Lemma 2.1[5]Forϕ∈it holds that

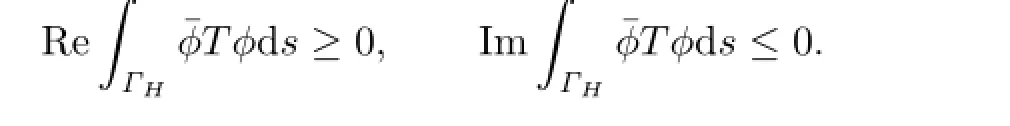
Lemma 2.2[9]∫If(2.6)holds,withFH∈thenγ+∫u=FHand

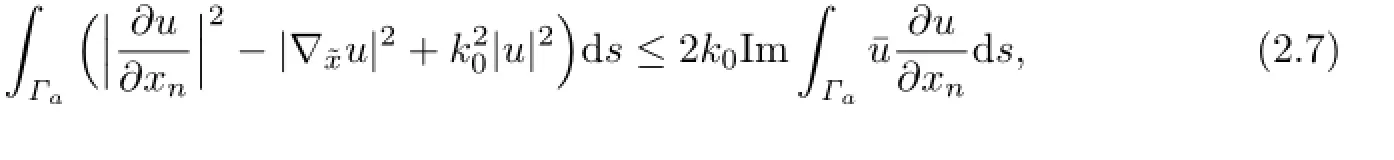
witha≥H.

Lemma 2.3[5]Foru∈VH,

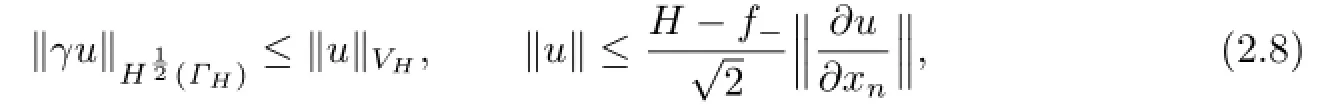
wheredenotes the induced norm of the scalar product(·,·)onL2(SH).

Now we are ready to introduce the sesquilinear form b:VH×VH→Cde fi ned by

Problem VWe formulate the variational problem:For g∈L2(SH), fi nd u∈VHsuch that

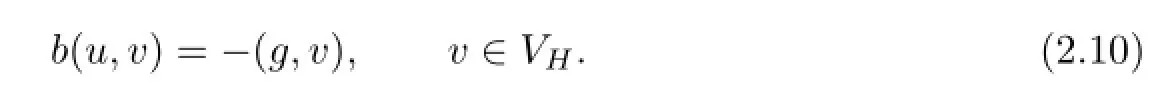
We have already known that the boundary value problem(2.4)–(2.6)is equivalent to the related variational problem,which is stated in the theorem as follows.

Theorem 2.1[9]Ifuis a solution of the boundary value problem(2.4)–(2.6),thensatis fi es the variational problem(2.10).Conversely,setFH:=and the de fi nition ofuis extended toDby(2.6),forx∈UH.Ifusolves the variational problem(2.10),then the extended function satis fi es the boundary value problem(2.4)–(2.6),withgextended by zero andkextended by taking the valuek0fromSHtoD.

3 Existence and Uniqueness for Non-absorbing Medium

In this section,we prove the equivalent variational problem.Thus the boundary value problem is uniquely solvable by establishing the inf-sup condition of the sesquilinear form, via application of the generalized Lax-Milgram theory of Babuska.Our methods of argument depend on a priori estimate established by means of a Rellich type identity and the results on approximation of nonsmooth by smooth domains.

Lemma 3.1[10]If the bounded sesquilinear formbsatis fi es the inf-sup condition

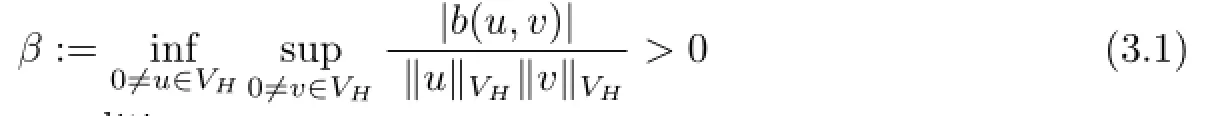
and the transposed inf-sup condition

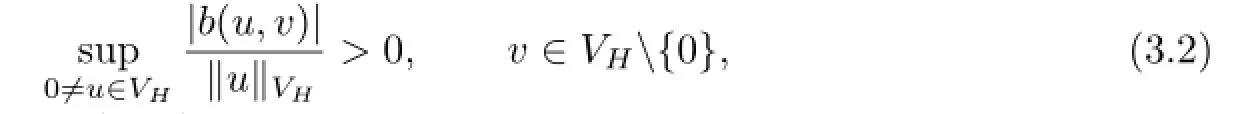
then the variational problem(2.10)has exactly one solutionu∈VHsuch that

In terms of the lemmas above,we could deduce the following result.

Theorem 3.1Suppose thatDsatis fi es the assumptions(2.1)–(2.2),and the wave numberksatis fi es(2.3).Then the variational problem(2.10)has a unique solutionu∈VHsuch that

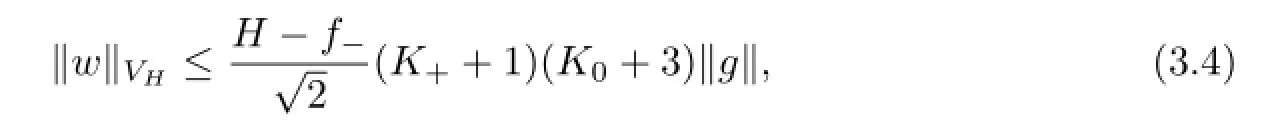
whereK+=k+(H−f−)andK0=k0(H−f−).

Since b is bounded(see[7])and the transposed inf-sup condition can be deduced by the inf-sup condition(see[5]),it suffice to establish(3.1).And we know that Lemmas 4.4–4.5, and Lemmas 4.10–4.11 in[5]reduce the problem of showing(3.1)to that of establishing an a priori bound for the solutions of the boundary problem when the boundaryΓis sufficiently smooth.Thus we need fi rst to establish a Rellich identity for the solution of Helmholtz equation.

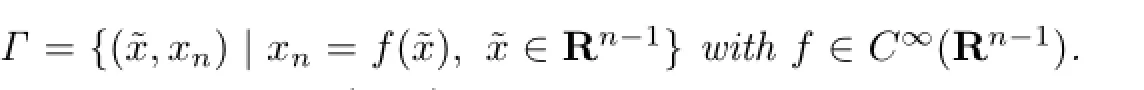
If u∈VHis a solution of the variational problem(2.10),then

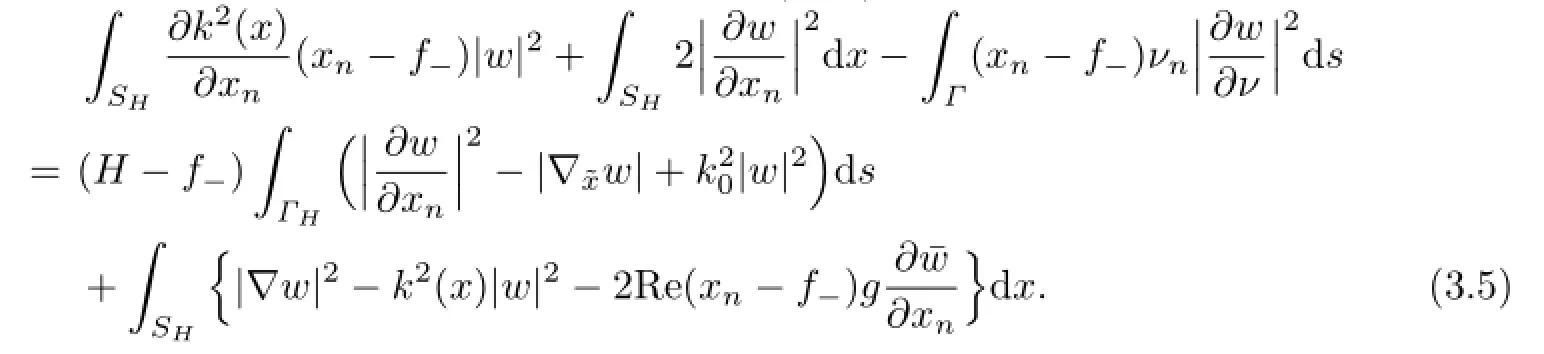
Proof.Let r=For A≥1,letsuch that 0≤ϕA≤1 with ϕA(r)=1,if r≤A;ϕA(r)=ϕA,if A＜r＜A+1;and ϕA(r)=0,if r≥A+1.Finallyfor some fi xed M＞0 independent of A.

It follows from Theorem 2.1 that,when extended to D by(2.6)with FH:=w satis fi es the boundary value problem with g extended by zero and k by k0from SHto D. Since the boundaryΓis smooth,by standard local regularity results(see[11]),we have u∈In view of this regularity,one has

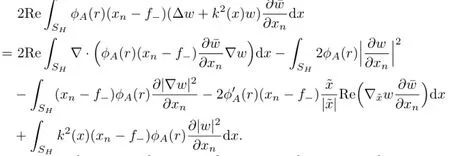
Furthermore,we use divergence theorem and integration by parts to obtainwhere ν is the unit outward normal derivative toΓ.Since w=0 onΓ,it holds thatand hence

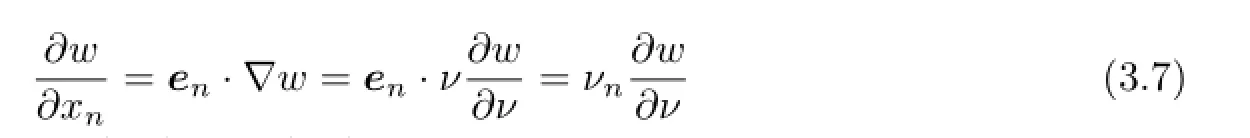
with νn=en·ν.Substituting(3.7)into(3.6)and rearranging terms yield

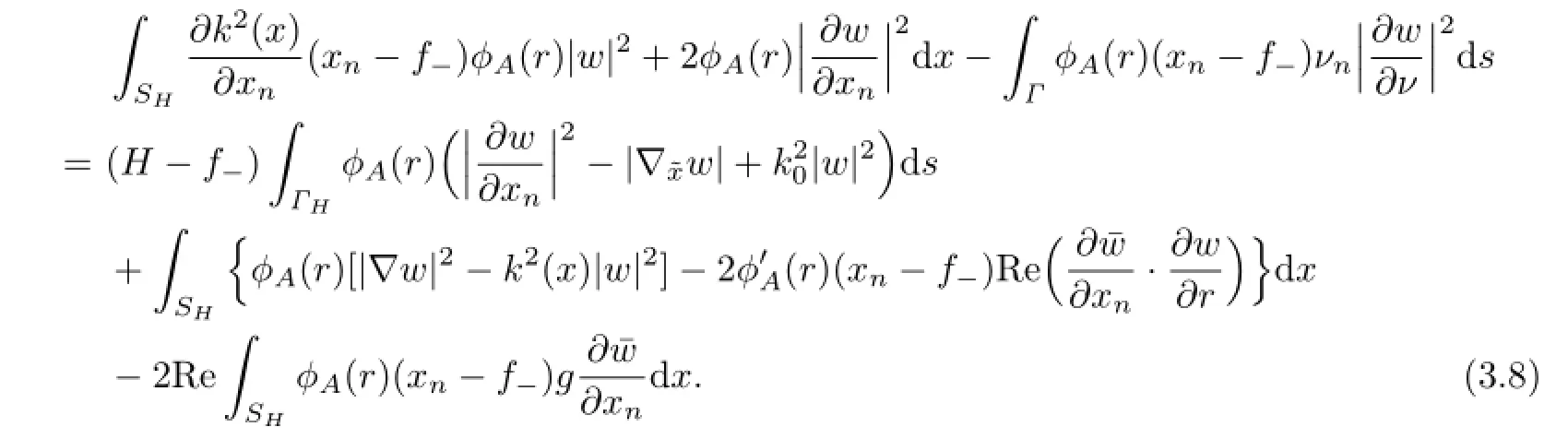
Next we try to estimate the terms in the above equality.LetThen

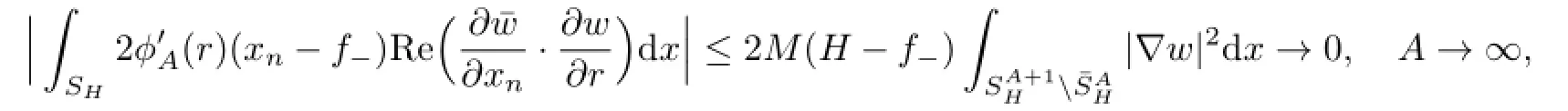
with w∈H1(SH).On the other hand,since w∈H2(UHUf+)(see[6]),one has∇w∈(ΓH).Thus taking the limit as A→∞in(3.8),we have

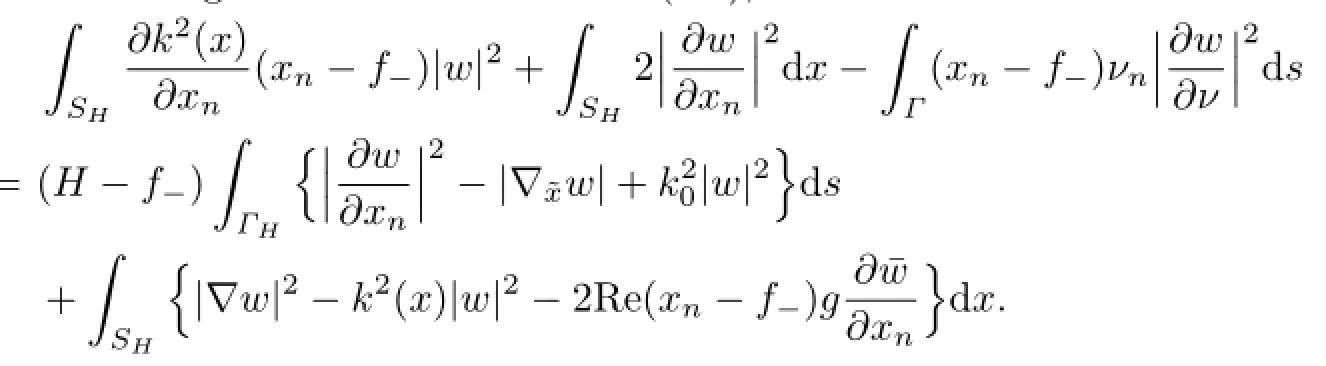
The Rellich identity above is our main tool to derive a priori estimate for a solution of the variational problem,which allows us to show an inf-sup condition for the sesquilinear form and thereby prove the well-posedness of the scattering problem.

L2(SH)andw∈VHwithH＞f+satisfy

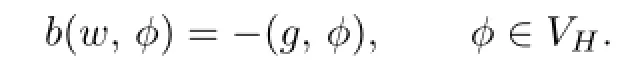
Then

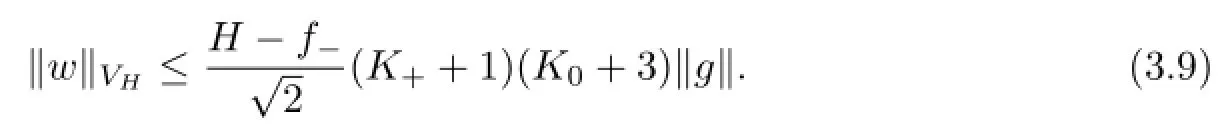
Proof.By Theorem 3.2,we directly have(3.5)for w.On the other hand,it follows from Lemma 2.2 that

∫

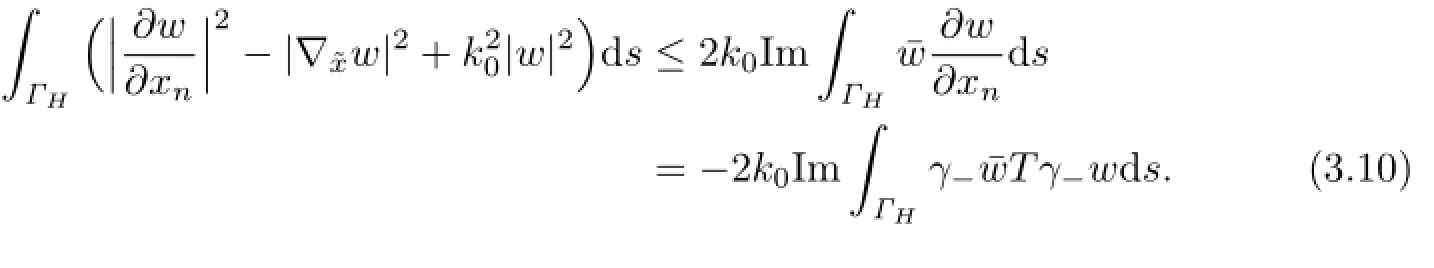
Moreover,since w satis fi es the variational problem,we conclude∫

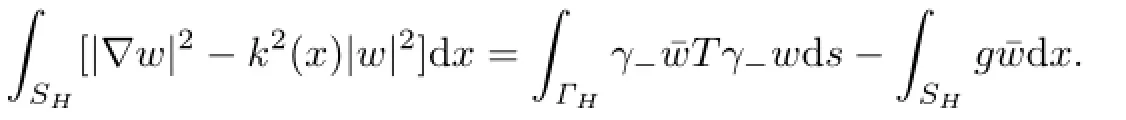
According to Lemma 2.1,it yields∫

and

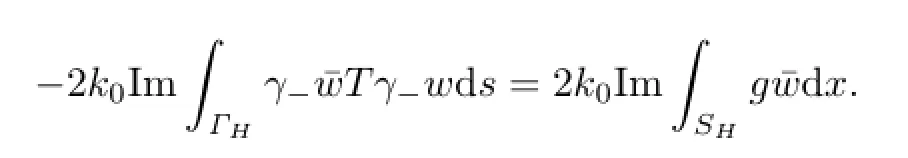
By using(3.5)and the inequalities(3.10)–(3.11),we obtain

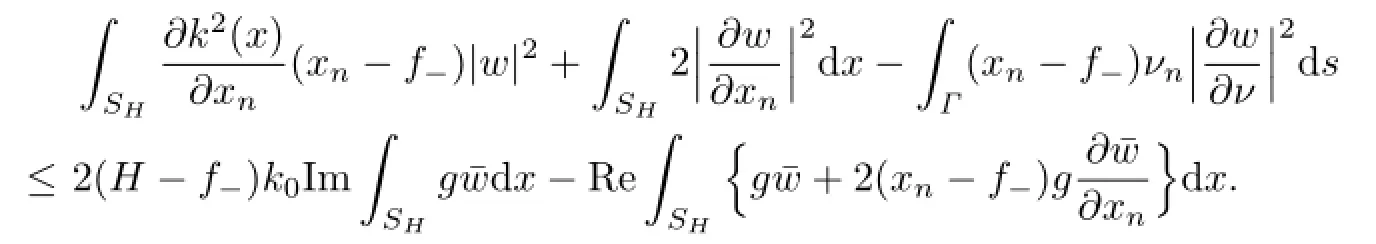
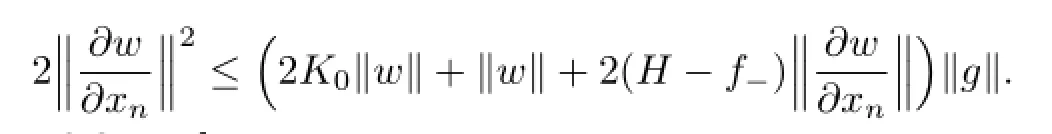
Thus,from Lemma 2.3,we have

and furthermore,

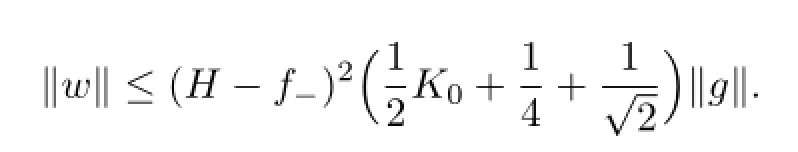
Then we deduce from(3.11)that

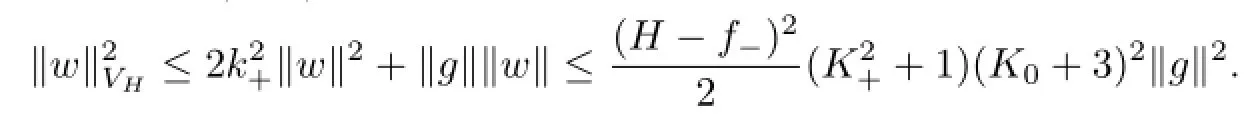
Hence,it holds that

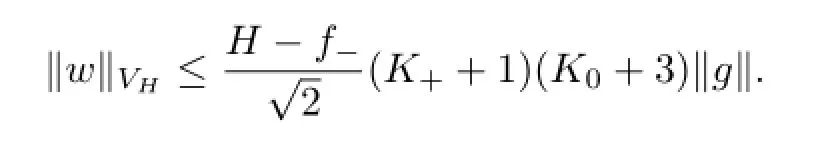
4 Existence and Uniqueness for Absorbing Media

After our study on non-absorbing layers,we now turn our interests to absorbing scatterers. We prefer to establish the uniqueness via an a priori bound which also leads to an existence result.We assume in this section that Re(k2)≥0,Im(k2)≥0 and Re(k2)≤Im(k2)≤

Theorem 4.1Suppose that the wave numberk∈Csatis fi es the assumption above.Then there exists a unique solutionu∈VHof the variational problem(2.10)such that

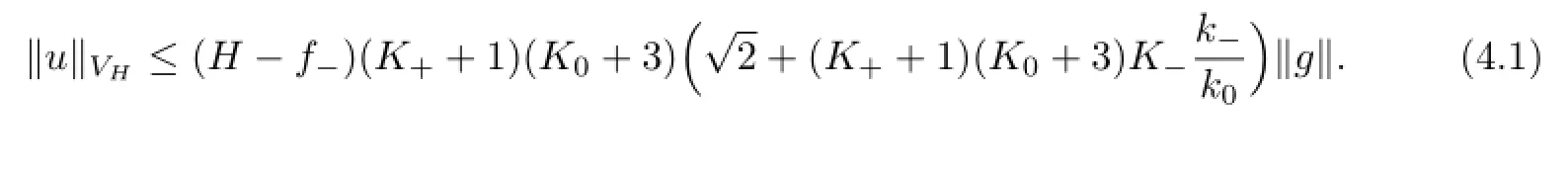
Proof.We rewrite the variational formulation(2.10)as

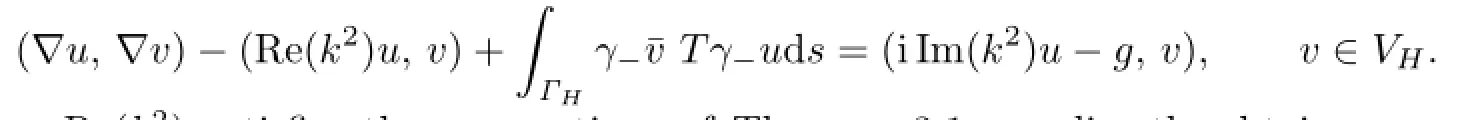
Because Re(k2)satis fi es the assumptions of Theorem 3.1,we directly obtain an a priori estimate for u,

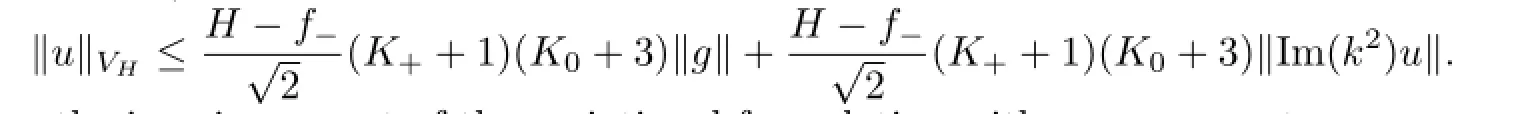
Taking the imaginary part of the variational formulation with v=u,we get∫

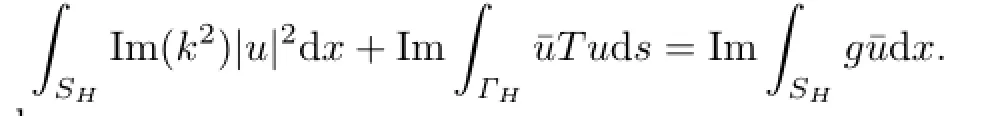
By Lemma 2.1,we have

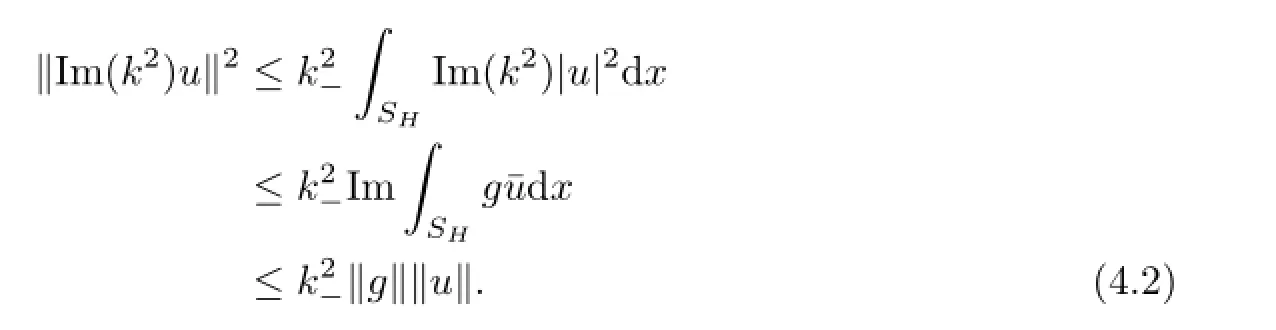
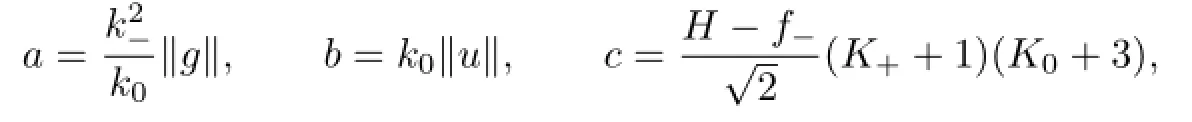
we have

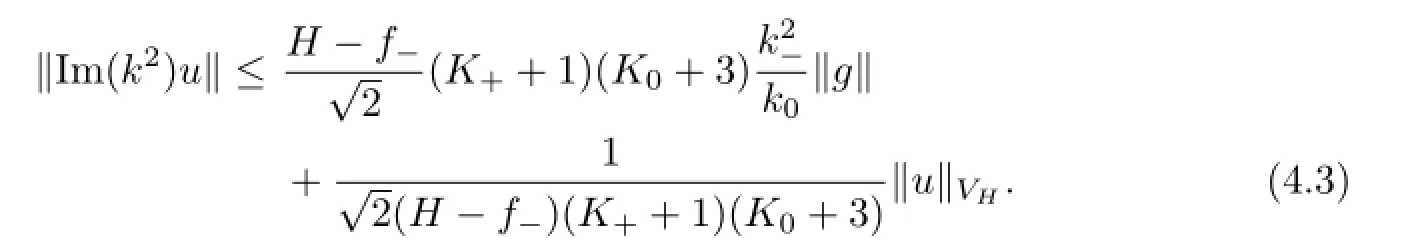
This allows us to conclude that

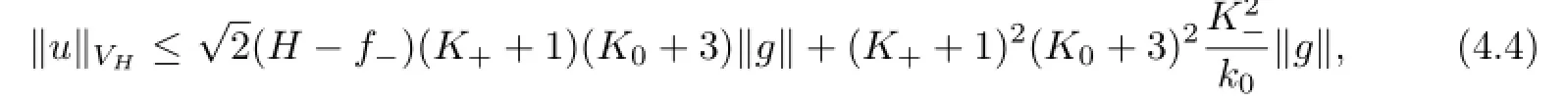
yielding an a priori estimate for u from which the existence and uniqueness of the solution to the variational problem follow.

5 Finite Element Approximation

In this section,we consider the numerical approach to solve the Problem V.We use the fi nite element method(FEM for short)to get the solution of the variational formulation(2.10). This is a classical approach for numerical treatment of the bounded domain problem.Thus a necessary fi rst step towards solving the Problem V numerically is to approximate it by a variational formulation on a domain of fi nite size,in which standard FEM can then be applied.This approximation consists simply in replacing SHby a fi nite regionde fi ned by:={X=(xn)∈SH:|˜x|＜R}and D by DR={X=(,xn)∈D:＜R}.

For R＞0,we approximate the problem(2.10)by a corresponding variational equation onLetdenote the Hilbert space VH.In the case that we replace D by DR,explicitlydenotes the completion ofwith the norm

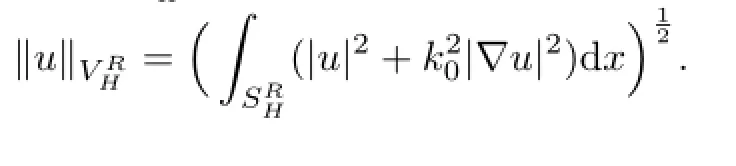
Problem AVThe approximating variational problem is as follows:Findsuch that

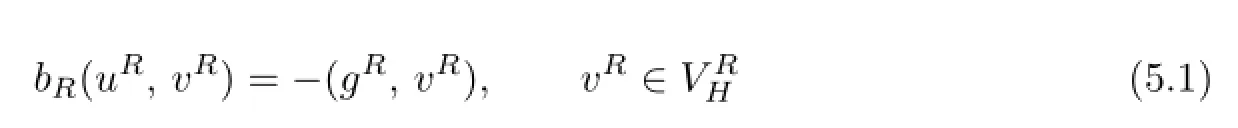
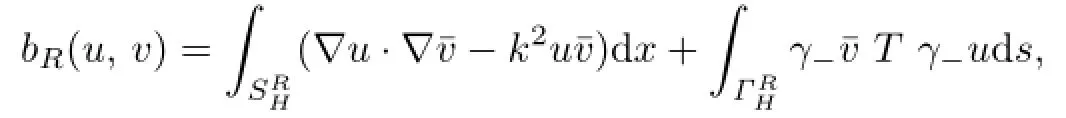
Let Thbe a regular triangulation partition of the computational domaininto elements K,and hKbe the diameter of K.Then we can de fi ne the step h=We denote the fi nite element space corresponding to Thby Vhconstructed by piecewise polynomials of degree p.If uIis the interpolation of uRin Vh,then there is a well-known approximation estimation(see[10])

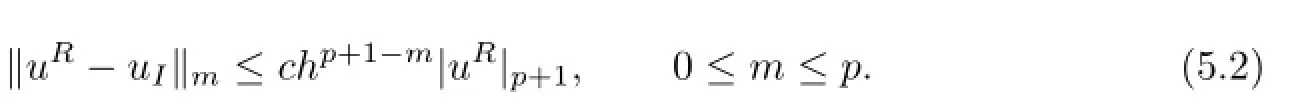
Here and in the sequel,c denotes a generic constant,which may have di ff erent values at di ff erent places.

Problem GAVWe consider the Galerkin approximation problem:Find∈Vhsatisfying

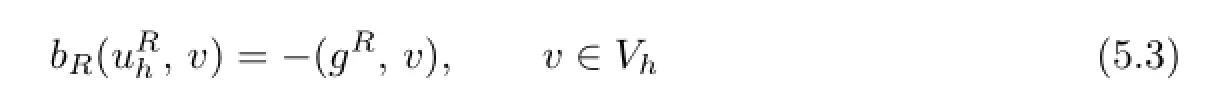
Since the inf-sup condition for the Problem V has been established by Theorem 3.1,it still holds for the Problem AV,which means that the Problem AV is well-posed.Meanwhile, we can also obtain the existence and the uniqueness of the solution for the Problem GAV by using the similar way used in Theorem 3.1.Furthermore,if eh=uR−we obtain by the de fi nition of bRthat

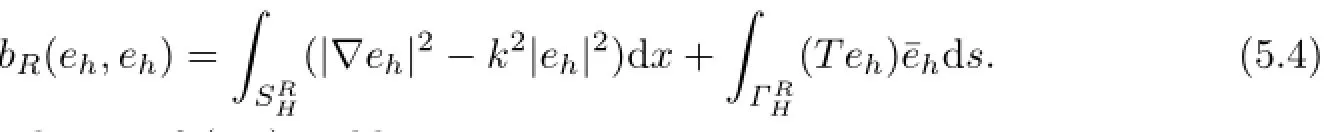
Then taking the real part of(5.4)yields

After rearranging terms,we have

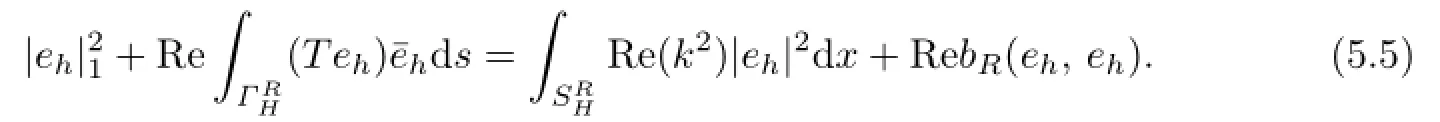
It is obvious that for any ϕ∈Vh,it holds that

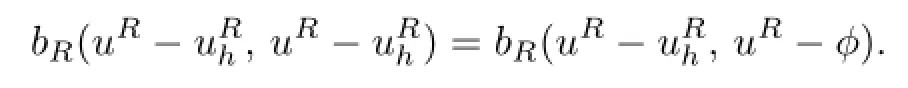
Thus

By the continuity of the operator T and the trace theorem,it holds that

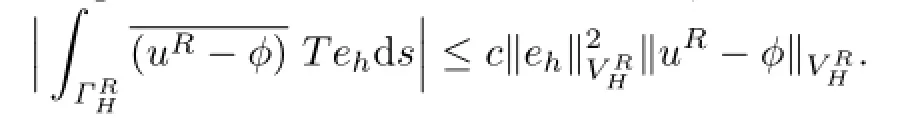
Together with the inequalities above,we get by means of the ε inequality that

Combining with(5.5)and selecting a sufficient small value of ε,we fi nally obtain

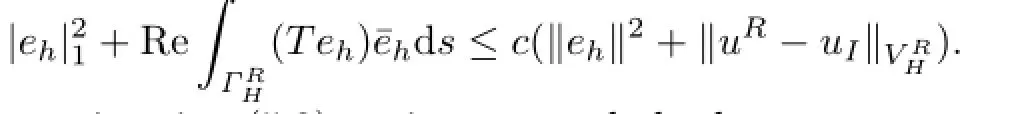
By the interpolation estimation(5.2)again,we conclude that

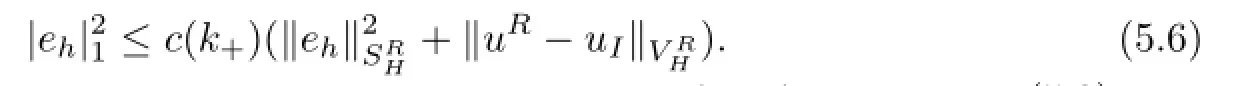
By the Aubin-Nitsche technique and the interpolation approximation property(5.2),one has

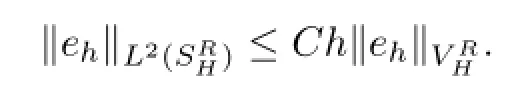
When h is small enough,it holds that

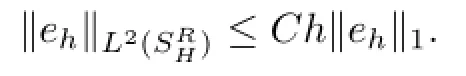
We further obtain from(5.6)that

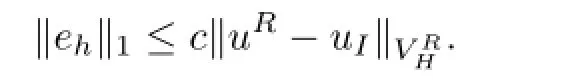
So we fi nally get the conclusion as follows.

Theorem 5.1Assume thatuR∈(s≥2)is the solution of the Problem AV. Then there exists anh0∈(0,1]such that forh∈(0,h0)the Problem GAV has a unique solutionand

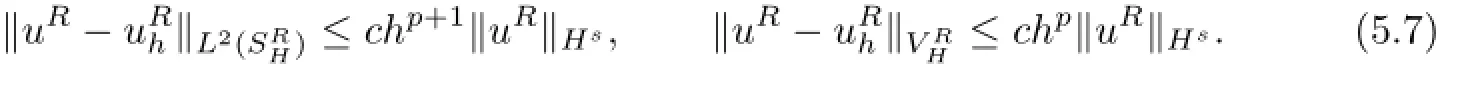
[1]Ogilvy J A.Theory of Wave Scattering from Random Rough Surfaces.Bristol:Adam Hilger, 1991.

[2]Sailard M,Sentence A.Rigorous solutions for electromagnetic scattering from rough surfaces. Waves Random Media,2001,11:103–137.

[3]Voronovich A G.Waves Scattering from Rough Surfaces.Berlin:Springer,1994.

[4]Wanick K,Chew W C.Numerical simulation methods for rough surface scattering.Waves Random Media,2001,11:1–30.

[5]Chandler S N,Monk P.Existence,uniqueness,and variational methods for scattering by unbounded rough surfaces.SIAM J.Math.Anal.,2005,37:598–618.

[6]Lechleiter A,Ritterbusch S.A variational for wave scattering from penetrable rough layers. IMA J.Appl.Math.,2010,75:366–391.

[7]Chandler S N,Monk P,Thomas P.The mathematics of scattering by unbounded,rough, inhomogeneous layers.J.Comput.Appl.Math.,2007,204:549–559.

[8]Monk P.Finite Element Methods for Maxwell’s Equations.New York:Oxford Univ.Press, 2003.

[9]Adams R A,Fourier J F.Sobolev Space.Oxford:Elsevier,2003.

[10]Ihlenburg F.Finite Element Analysis of Acoustic Scattering.New York:Springer,1998.

[11]Gilbarg D,Trudinger N S.Elliptic Partial Di ff erential Equations of Second Order.Berlin: Springer,1983.

tion:47J30,65N30

A

1674-5647(2014)01-0071-10

Received date:Oct.24,2011.

Foundation item:The Education Department(12531136)of Heilongjiang,the NSF(10971083,51178001)of China,Science and Technology Research Project(2014213)of Jilin Province Department of Education.

E-mail address:luantian@163.com(Luan T).