Numerical Solution for Fractional Partial Differential Equation with Bernstein Polynomials
Jin-Sheng Wang, Li-Qing Liu, Yi-Ming Chen, and Xiao-Hong Ke
Numerical Solution for Fractional Partial Differential Equation with Bernstein Polynomials
Jin-Sheng Wang, Li-Qing Liu, Yi-Ming Chen, and Xiao-Hong Ke
—A framework to obtain numerical solution of the fractional partial differential equation using Bernstein polynomials is presented. The main characteristic behind this approach is that a fractional order operational matrix of Bernstein polynomials is derived. With the operational matrix, the equation is transformed into the products of several dependent matrixes which can also be regarded as the system of linear equations after dispersing the variable. By solving the linear equations, the numerical solutions are acquired. Only a small number of Bernstein polynomials are needed to obtain a satisfactory result. Numerical examples are provided to show that the method is computationally efficient.
Index Terms—Absolute error, Bernstein polynomials, fractional partial differential equation, numerical solution, operational matrix.
1. Introduction
Fractional calculus is an old mathematical topic, which is generalized from integer order ones and achieved by replacing integer order derivatives by fractional ones. Fractional differential equations are used widely to model natural physical process and dynamic systems, and they are more accurate than integer differential equations[1]. In recent years, both mathematicians and physicists have devoted considerable efforts to seek the numerical and analytical methods of fractional differential equations. The most commonly used methods are Adomian decomposition method (ADM)[2],[3], Variational iteration method (VIM)[4], generalized differential transform method (GDTM)[5]-[7], dinite difference method (FDM)[8], and wavelet method[9],[10]and so on.
In this paper, our study focuses on a class of fractional partial differential equation as follows:
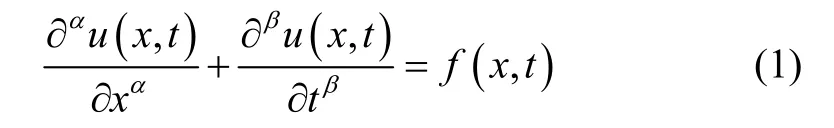
subject to the initial conditions
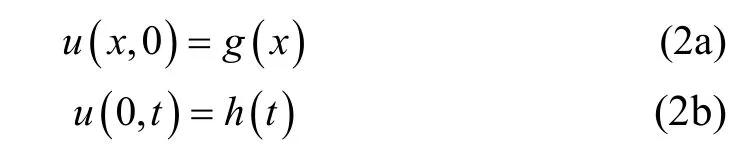
There have been several methods for solving the fractional partial differential equation. For example, by using generalized differential transform method, Odibat successfully obtained the numerical solution of linear partial differential equations of fractional order[7]; with the Laplace Transform method, Podlubny solved the fractional partial differential equations with constant coefficients[11].
In this paper, we introduce the Bernstein polynomials to seek the numerical solution of fractional partial differential equations. With the simple structure and perfect properties[12]-[15], Bernstein polynomials play an important role in various areas of mathematics and engineering. Those polynomials have been widely used in the solution of integral equations and differential equations[12]-[17].
The reminder of the paper is organized as follows. In Section 2, the basic fractional derivatives and integrals definitions are briefly reviewed. The basic definitions of Bernstein polynomials, function approximation, and convergence analysis in Bernstein polynomials are given in Section 3. In Section 4, the fractional operational matrices of Bernstein polynomials are derived and used to solve the equation at beginning. In Section 5, we present numerical examples to illustrative the method and to demonstrate the efficiency of the method. We end the paper with a few concluding remarks in Section 6.
2. Definitions of Fractional Derivatives and Integrals
In this section, we give some basic definitions and some properties of fractional calculus. With the development of theories of fractional derivatives and integrals, there are many definitions appeared, such as theRiemann-Liouville and Caputo fractional differential integral definitions[11].
1) Riemann-Liouville fractional integral of order
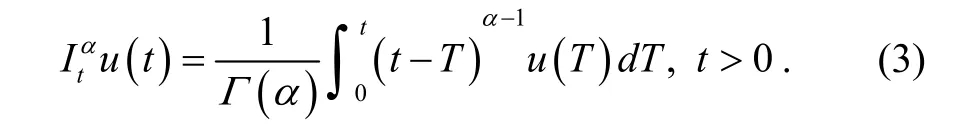
The properties of the Riemann-Liouville fractional integral can expressed as
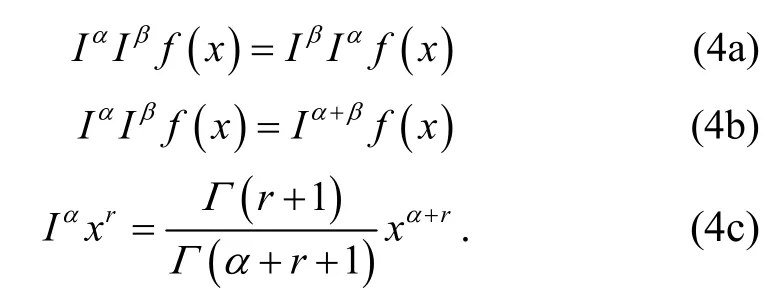
2) Riemann-Liouville fractional derivative of order
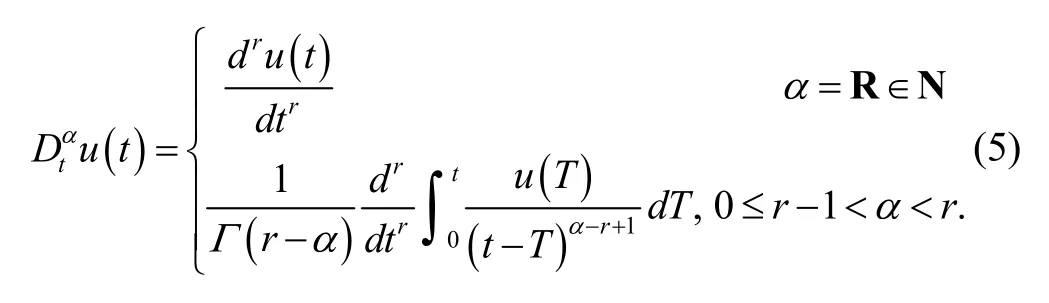
The Riemann-Liouville fractional derivative has certain disadvantages when trying to model real-world phenomena using fractional differential equations. So, we will introduce a modified fractional differential operator by Caputo’s work.
3) Caputo’s fractional derivative of order
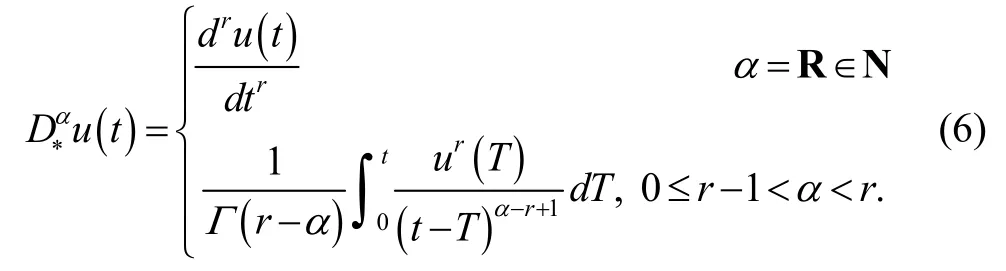
Particularly, for the Caputo derivative we have (cis a constant)
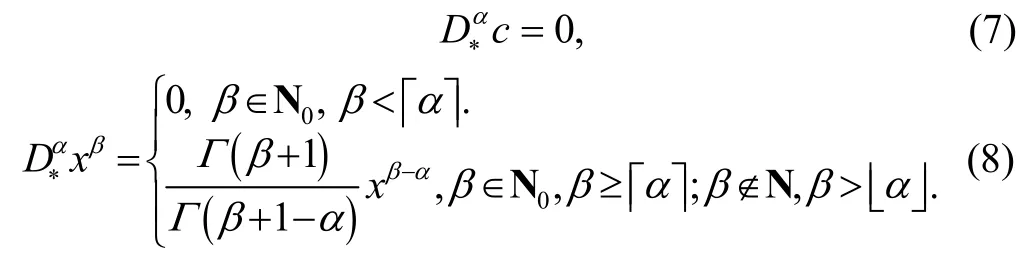
The relation between the Riemann-Liouville operator and Caputo operator is given by the following expressions.
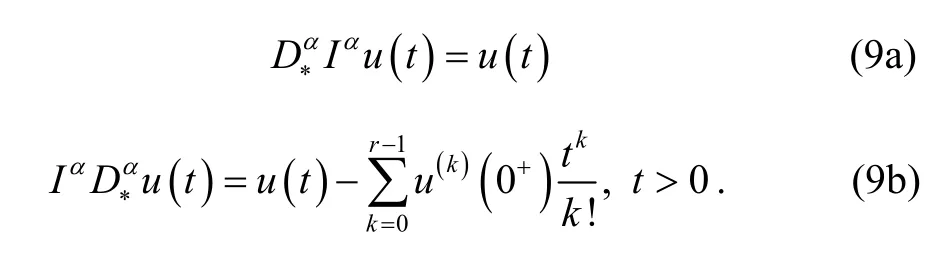
3. Bernstein Polynomials and Properties
3.1 Definition of Bernstein Polynomials Basis
The Bernstein polynomials of degreenare defined by
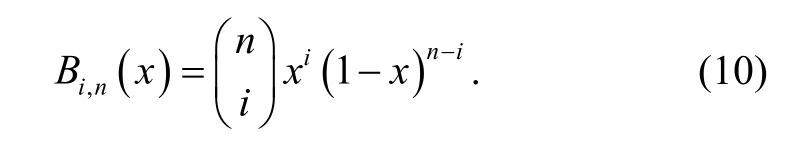
By using the binomial expansion of, (10) can be expressed as
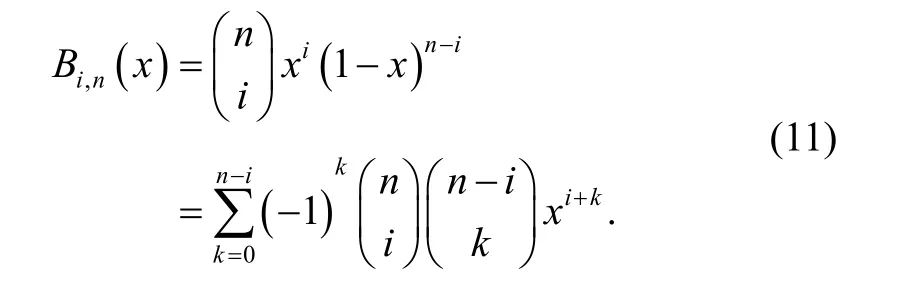
Now, we define
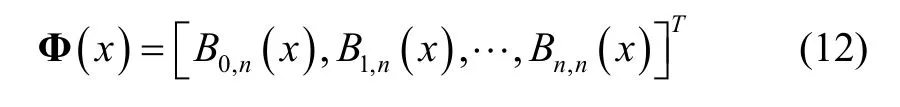
where

and
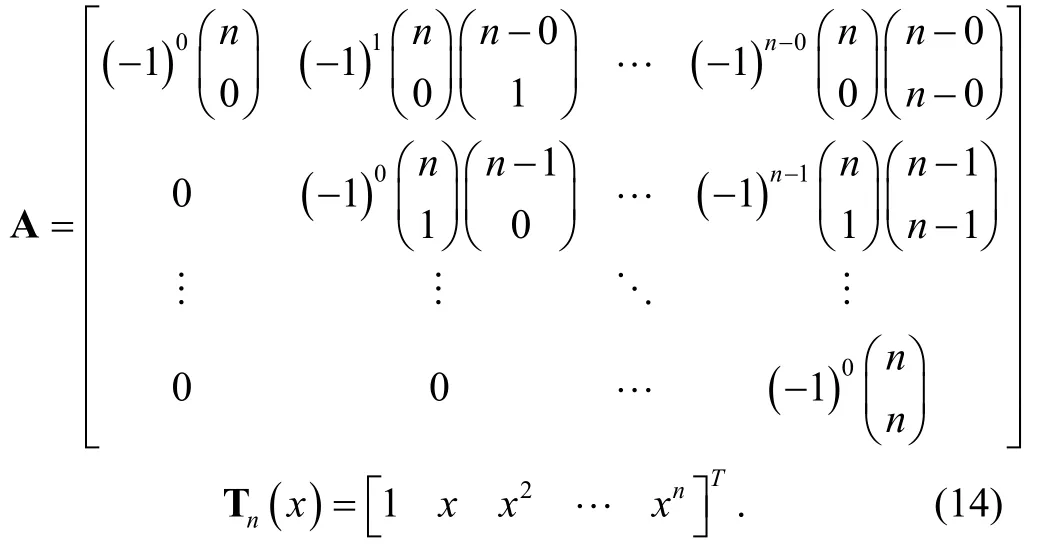
It is obvious that
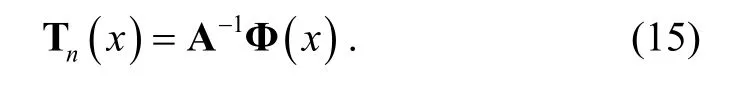
3.2 Function Approximation
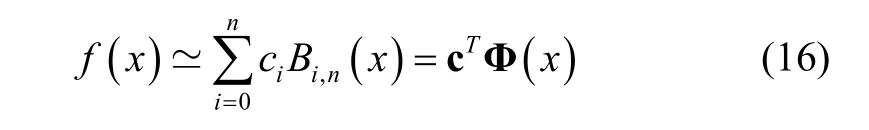
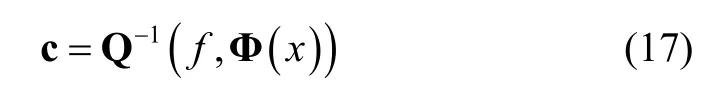
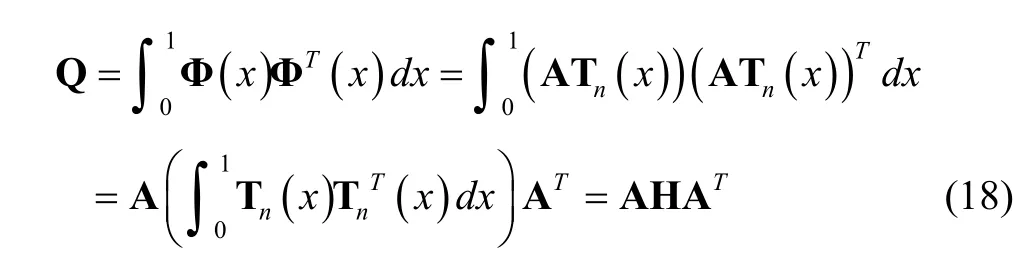
whereHis a Hilbert matrix:
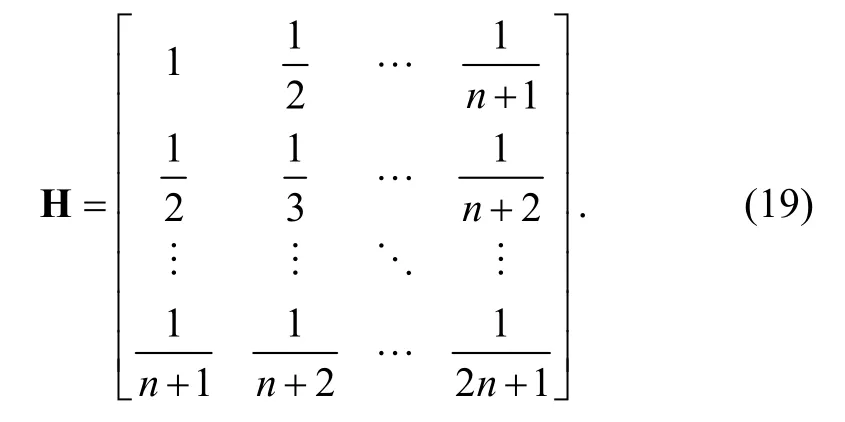
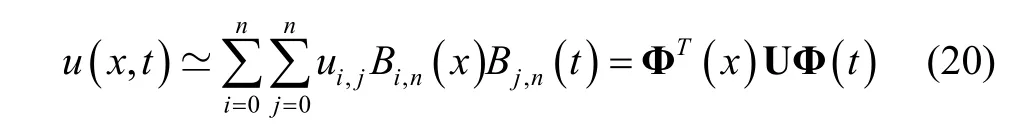
where
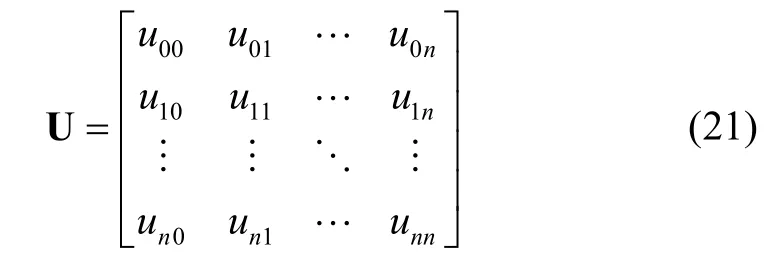
Ucan be obtained as follows:
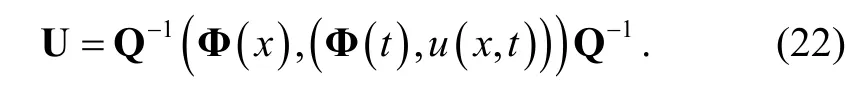
3.3 Convergence Analysis
Suppose that the functionfism+1 times continuously differentiable, that is to sayandis the best approximation offout of Y, then the mean error bound is presented as follows:
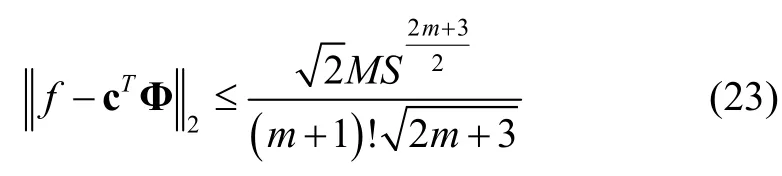
Proof.We consider the Taylor polynomials
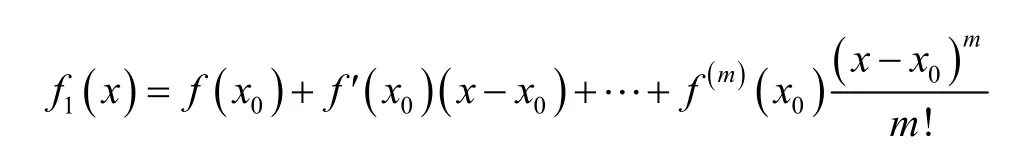
which we know
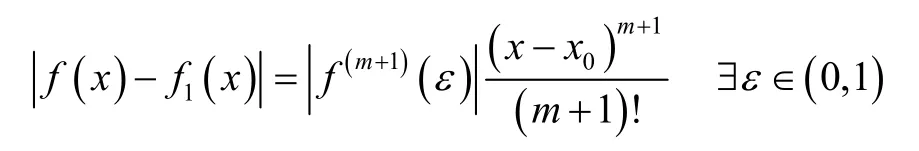
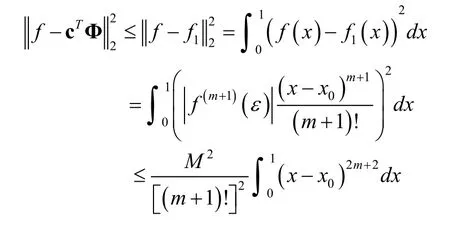
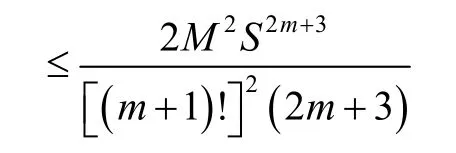
and taking square roots we have the above bound.
3.4 Proposed Method for the Numerical Solution of the Fractional Partial Differential Equation
Now, consider the fractional partial differential equation given by (1) and (2).
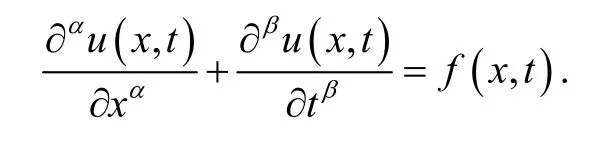
If we approximate the functionwith Bernstein polynomials, it can be written as (20), then we have
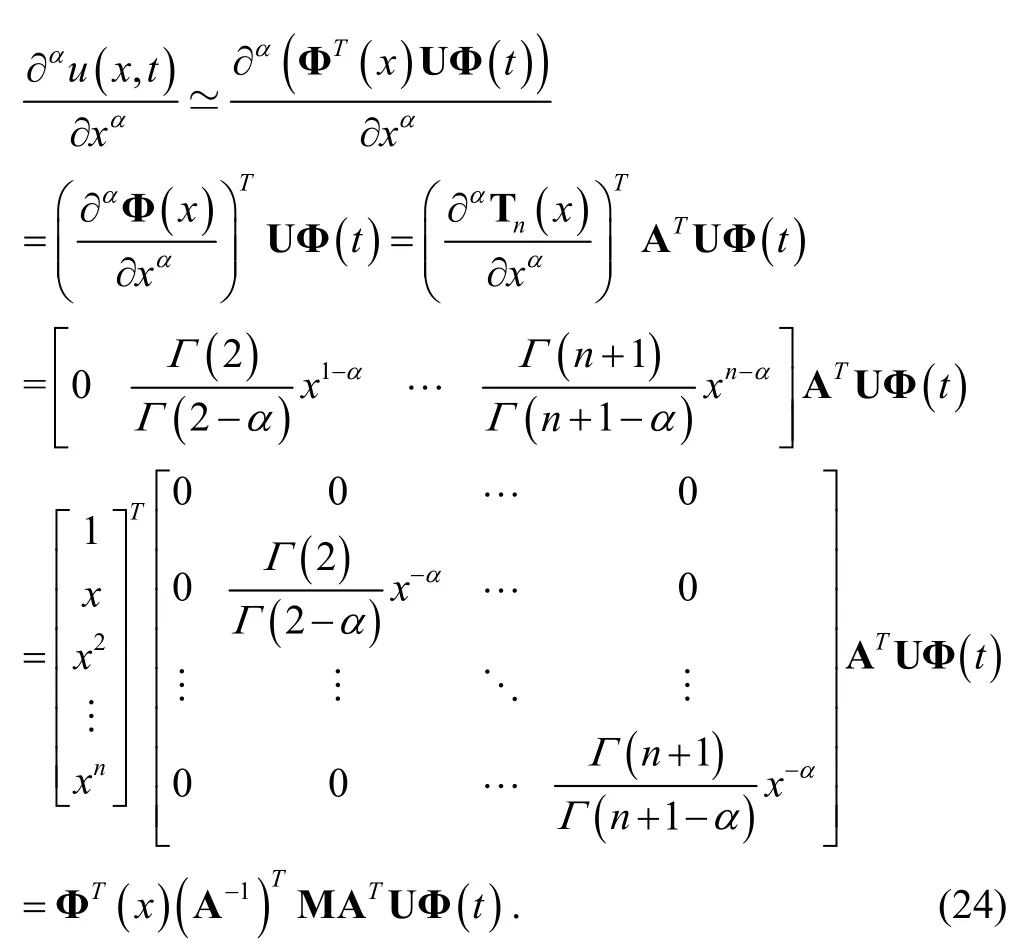
We define
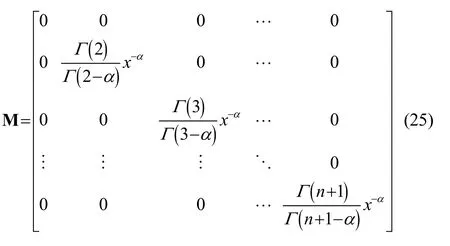
whereMis called the fractional order operational matrix of Bernstein polynomials. Similarly, we can get
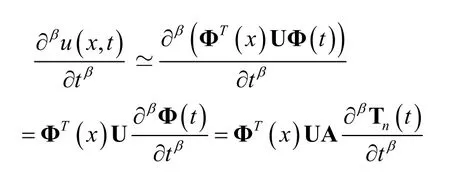

and we define
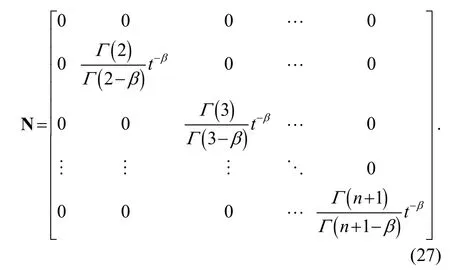
whereNis also called the fractional order operational matrix of Bernstein polynomials.
Substituting (24) and (26) into (1), we have
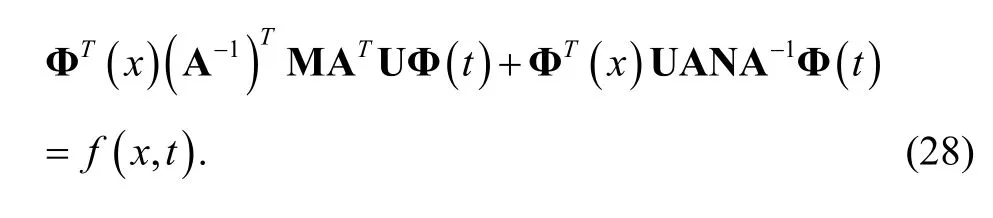
Dispersing (28) by the pointswe can obtainUwhich is unknown.
4. Numerical Examples
To demonstrate the efficiency and the practicability of the proposed method based on Bernstein polynomials method, we consider the following examples.
Example 1:
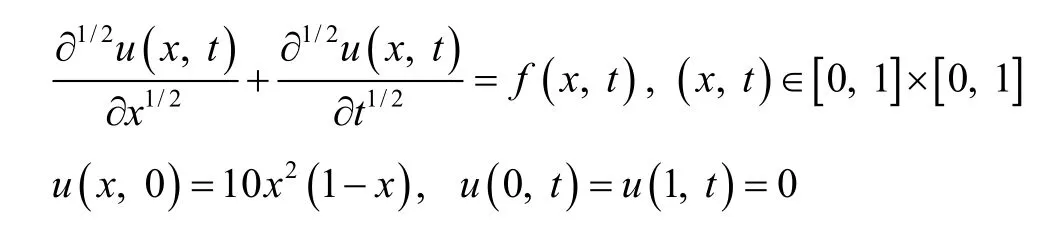
where
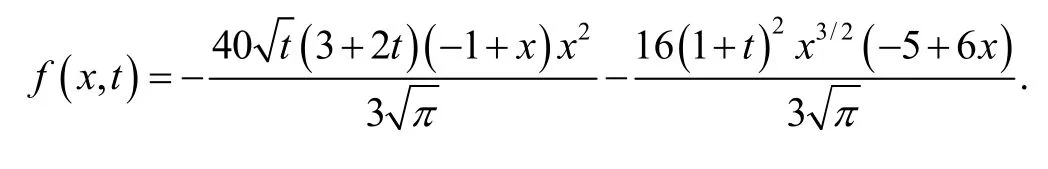
The exact solution of the above equation is
We solve the problem by adopting of the technique described in Section 3 and by making use of Mathematica. When 2n= , dispersing
the matrixUis displayed as follows:

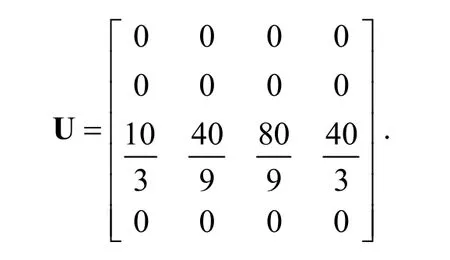
When 3n= , dispersing
the matrixUis displayed as follows:
when 4n= , dispersing
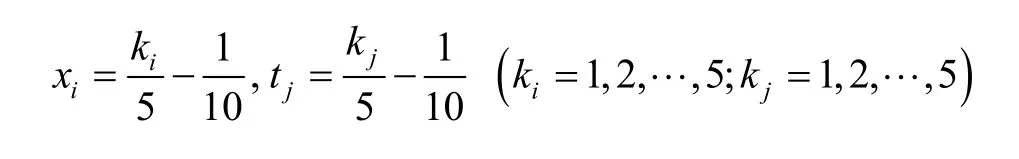
the matrixUis displayed as follows:
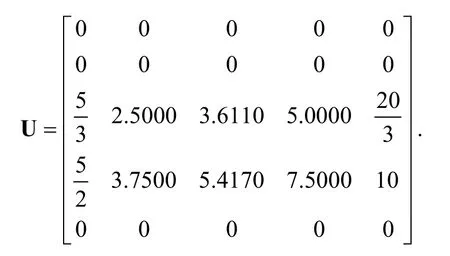
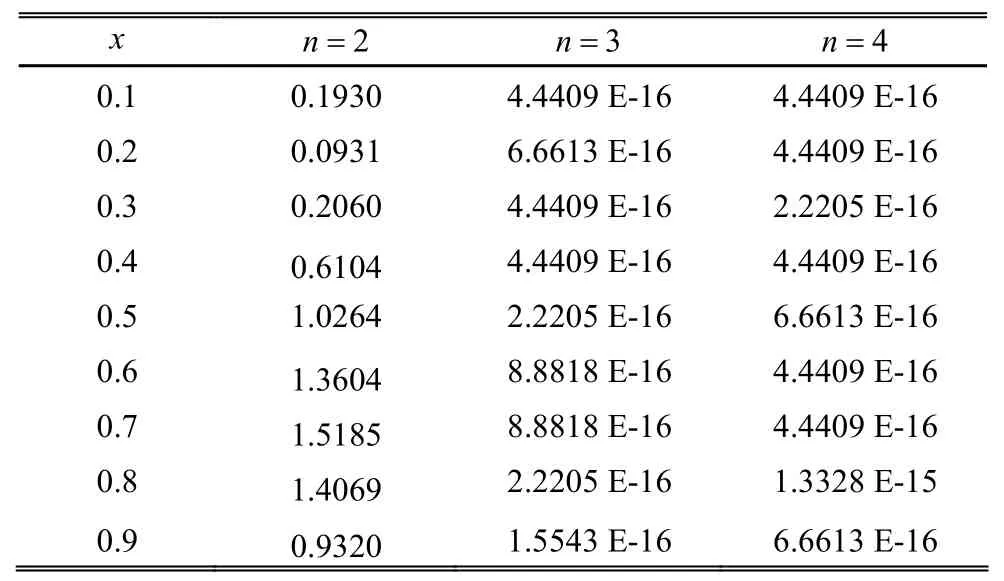
Table 1: Absolute error for t=1/4 for different values of n
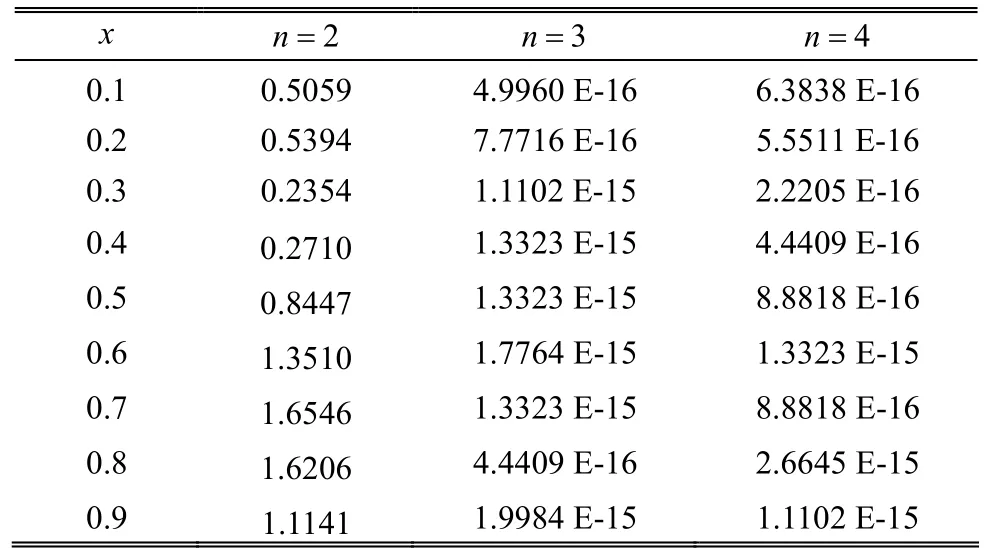
Table 2: Absolute error for t=1/2 for different values of n
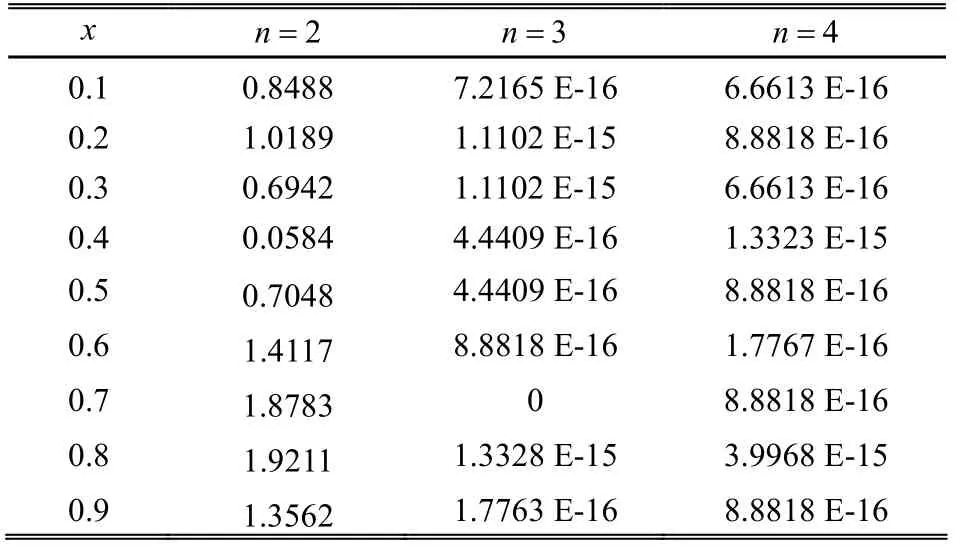
Table 3: Absolute error for t=3/4 for different values of n
From Table 1 to Table 3, we can see that the absolute error is very tiny and only a small number of Bernstein polynomials are needed when 3n≥ . When 2n= , it is not surprising that the absolute error is very big. With the polynomials of degree 2th to approximate the polynomials of degree 3th, we cannot obtain satisfactory results.
Also whennis definite, the more points we take, the more accurate solution we get. Fig. 1 to Fig. 3 explain the fact. (we taken=3,,xtnis the number of thexi,tj).
Example 2:
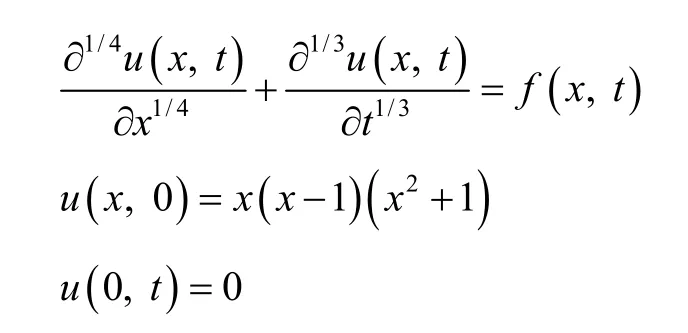
where
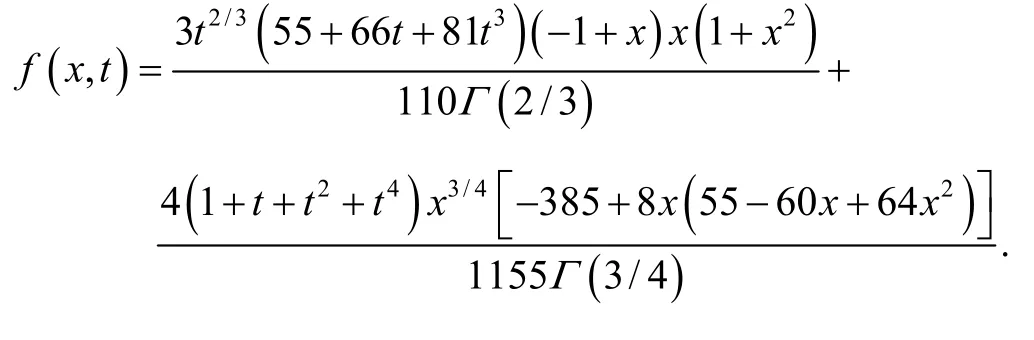
The exact solution is
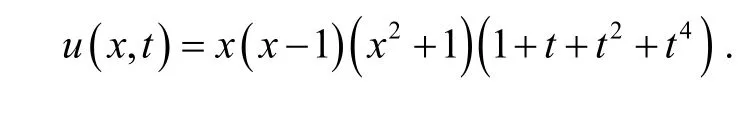
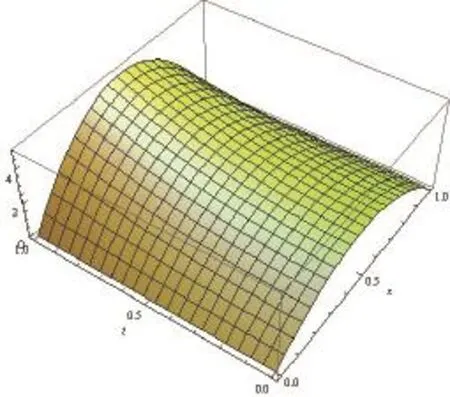
Fig. 1. Numerical solution of
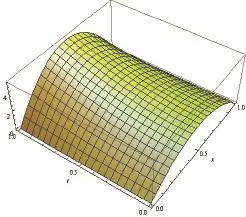
Fig. 2. Numerical solution
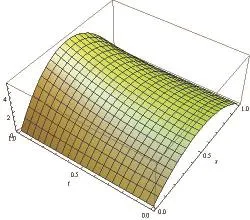
Fig. 3. Exact solution.
When 4n= , dispersing
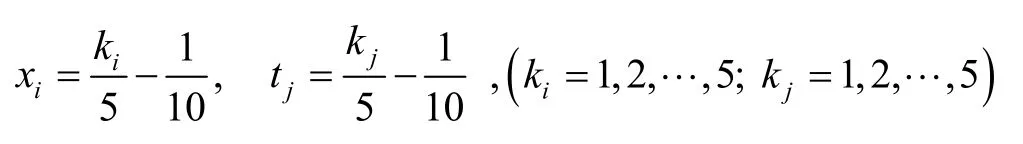
and the matrixUis displayed as follows:
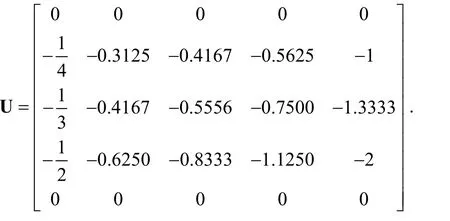
The absolute error is displayed Fig. 4.
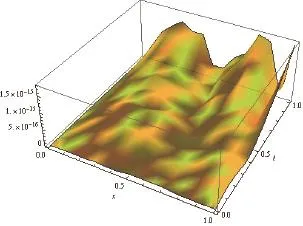
Fig. 4. Absolute error when n=4.
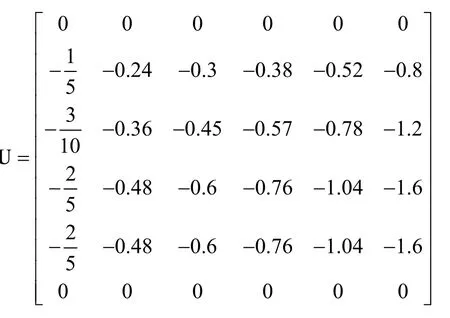
When 5n= , dispersing
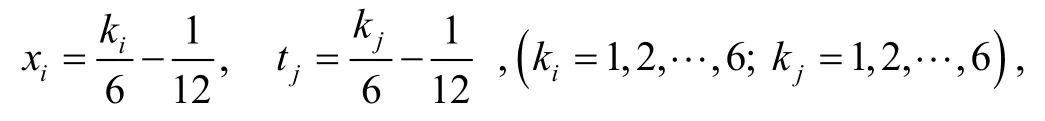
the matrixUis displayed as follows:
The absolute error is displayed Fig. 5.
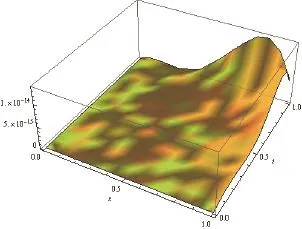
Fig. 5. Absolute error when n=5.
Example 3:
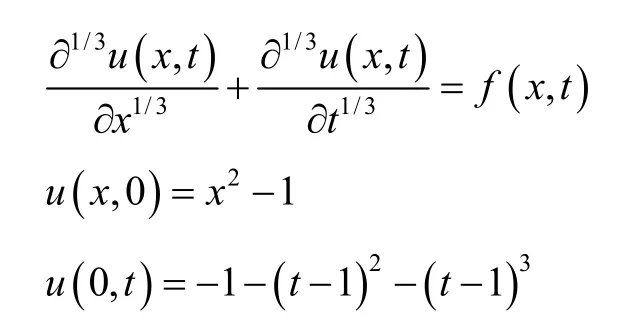
where
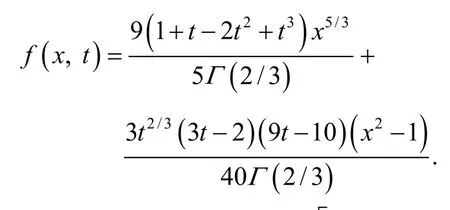
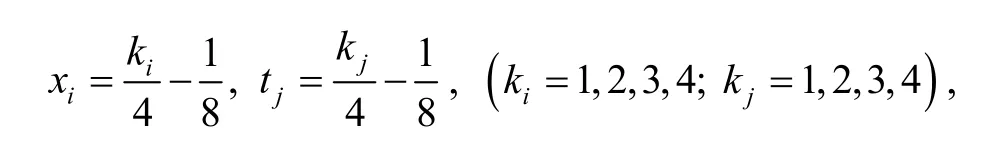
the matrixUis displayed as follows:
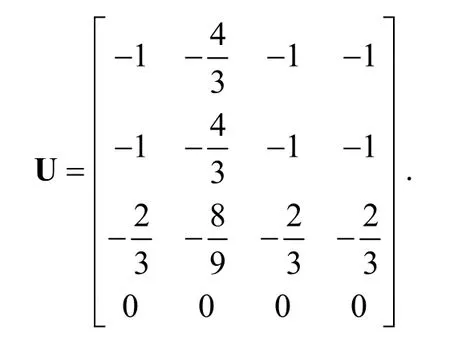
The absolute error is displayed in Fig. 6.

Fig. 6. Absolute error when n=3.
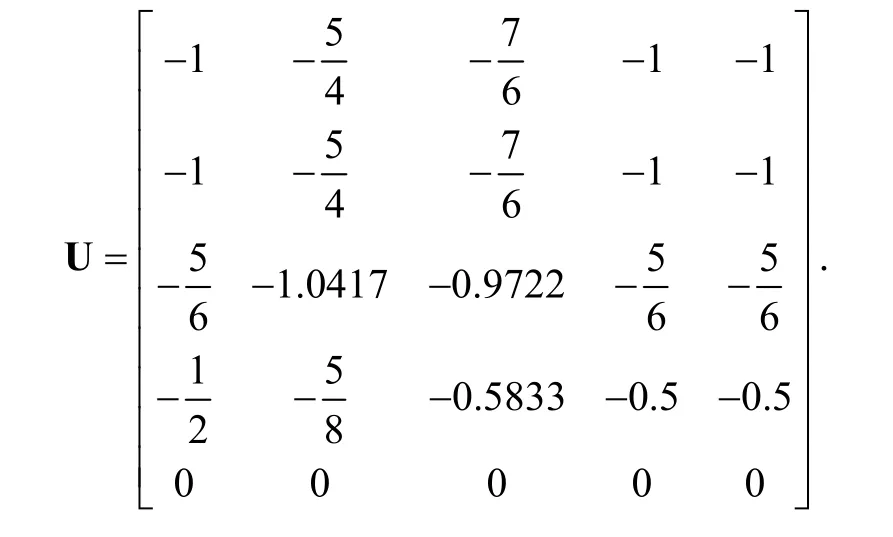
The absolute error is displayed in Fig. 7.
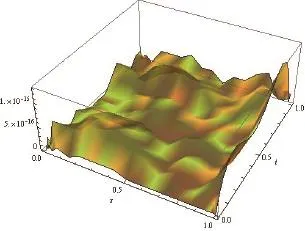
Fig. 7. Absolute error when n=4.
From Example 1 to Example 3, we can find that the method in this article can be effectively used in the numerical solution of the fractional partial differential equation. At the same time the feasibility of the method is also proved. From the above results, the numerical solutions are in good agreement with the exact solution. We draw a conclusion that the method is not only effective to get the numerical solution with good coincidence, but also more accurate than other methods.
5. Conclusions
This article solves a class of fractional partial differential equations by combining Bernstein polynomials with the properties of fractional differentiation. We translate the initial equation into the product of some relevant matrixes which can also be viewed as the system of linear equations after dispersing the variable. With the least square method, we can solve the equations easily.
There are quite a lot of methods to solve fractional partial differential equations such as the block pulse operational matrix method, and wavelet method. With the Bernstein polynomials method, the absolute error is 10-15, so it is more perfect than other methods. What is more, the method in this paper is easy implementation.
Acknowledgements
This work was supported by Qinhuangdao Research and Development Program of Science and Technology under Grant No. 201201B019, and Qinhuangdao Technology Bureau 2013 Research and Development Projects of Science and Technology under Grant No. 201302A023.
The authors are very grateful to both referees for their comments and suggestions. Also authors are very thankful to the associate editor for the comments which have improved the paper.
[1] L. Galue, S. L. Kalla, and B. N. Al-Saqabi, “Fractional extensions of the temperature field problems in oil strata,”Appl. Math. Comput, vol. 186, pp. 35-44, March 2007.
[2] A. EI-Sayed, “Nonlinear functional differential equations of arbitrary orders,” Nonliear Analysis, vol. 33, no. 2, pp. 181-186, Jul. 1998.
[3] I. L. EI-Kalla, “Error estimate of the series solution to a class of nonlinear fractional differential equations,”Commun. Nonlinear Sci. Numer. Simulat, vol. 16, pp. 1408-1403, Mar. 2011.
[4] Z. M. Odibat, “A study on the convergence of variational iteration method,” Mathematical and Computer Modeling, vol. 51, pp. 1181-1192, May. 2010.
[5] S. Momani and Z. Odibat, “Generalized differential transform method for solving a space and time-fractional diffusion-wave equation,” Physics Letters A, vol. 370, pp. 379-387, Oct. 2007.
[6] Z. Odibat and S. Momani, “Generalized differential transform method: Application to differential equations of fractional order,” Applied Mathematics and Computation, vol. 197, pp. 467-477, Apr. 2008.
[7] Z. Odibat and S. Momani, “A generalized differential transform method for linear partial differential equations of fractional order,” Applied Mathematics Letters, vol. 21, pp. 194-199, Feb. 2008.
[8] Y. Zhang, “A finite difference method for fractional partial differential equation,” Applied Mathematics and Computation. vol. 215, pp. 524-529, Sep. 2009.
[9] Y.-X. Wang and Q.-B. Fan, “The second kind Chebyshev wavelet method for solving fractional differential equations,” Applied Mathematics and Computation, vol. 218, pp. 8592-8601, May 2012.
[10] M.-X. Yi and Y.-M. Chen, “Haar wavelet operational matrix method for solving fractional partial differential equations,”Computer Modeling in Engineering & Sciences, vol. 88, no. 3, pp. 229-244, Dec. 2012.
[11] I. Podlubny, Fractional Differential Equations, San Diego: Academic Press, 1999.
[12] Y.-M. Chen, M.-X. Yi, C. Chen, and C.-X. Yu, “Bernstein polynomials method for fractional convection-diffusion equation with variable coefficients,” Computer Modeling in Engineering & Sciences, vol. 83, no. 6, pp. 639-653, Apr. 2012.
[13] K. Maleknejad, E. Hashemizadeh, and B. Basirat,“Computational method based on Bernstein operational matrices for nonlinear Volterra-Fredholm-Hammerstein integral equations,” Commun. Nonlinear Sci. Numer. Simul. vol. 17, no. 1, pp. 52-61, Jan. 2012.
[14] S. A. Yousefi and M. Behroozifar, “Operational matrices of Bernstein polynomials and their applications,” Int. J. Systems Sci. vol. 41, no. 6, pp. 709-716, Mar. 2010.
[15] S. A. Yousefi, M. Behroozifar, and M. Dehghan, “The operational matrices of Bernstein polynomials for solving the parabolic equation subject to specification of the mass,”Journal of Computational and Applied Mathematics, vol. 235, pp. 5272-5283, Jul. 2011.
[16] E. H. Doha, A. H. Bhrawy, and M. A. Saker, “Integrals of Bernstein polynomials: An application for the solution of high even-order differential equations,” Appl. Math. Lett., 24, vol. 24, pp. 559-565, Apr. 2011.
[17] K. Maleknejad, E. Hashemizadeh, and R. Ezzati, “A new approach to the numerical solution of Volterra integral equations by using Bernsteins approximation,” Commun Nonlinear Sci. Numer. Simula.t, vol. 16, pp. 647-655, Feb. 2011.
[18] T. J. Rivlin, An Introduction to the Approximation of Functions, New York: Dover Publications, 1969.

Jin-Sheng Wangwas born in Jilin, China in 1967. He received his B.S. degree in Jilin Polytechnical University in 1990, and the M.S. degree in Yanshan University in 1999. He is now a lecturer with the School of Continuing Education, Yanshan University. His research interests include measurement and application.

Li-Qing Liuwas born in Hebei, China in 1988. She received the B.S. degree from Hebei Normal University of Science and Technology in 2102. She is currently pursuing the M.S. with Yanshan University. Her research interests include numerical solution of differential equation and so on.

Yi-Ming Chenwas born in Heilongjiang, China in 1957. He obtained his Ph.D. degree from Yanshan University, Qinhuangdao in 2002. He was a post-doctor from 2005 to 2007 in Glamorgan University, UK. He is now a professor with the College of Science, Yanshan University,China. His research interests include boundary element method in contact problem, boundary element solution for the variation inequality, and numerical solution of differential equation.

Xiao-Hong Kewas born in Liaoning, China in 1989. She received the B.S. degree from Shenyang Normal University in 2102. She is currently pursuing the M.S. in Yanshan University. Her research interests include numerical solution of differential equation and so on.
Manuscript received January 10, 2014; revised February 12, 2014. This work was supported by the Natural Science Foundation of Hebei Province under Grant No. A2012203407.
L.-Q. Liu is with the Institute of College of Science, Yanshan University, Qinhuangdao 066000, China (Corresponding author e-mail: liuliqing_yanyan@163.com).
J.-S. Wang and Y.-M. Chen are with the Institute of School of Continuing Education Yanshan University, Qinhuangdao 066000, China (e-mail:wjinsheng2010@163.com; chenym@ysu.edu.cn).
X.-H. Ke is with the Institute of College of Science, Yanshan University, Qinhuangdao 066000, China (e-mail:kexiaohong1989@163.com)
Digital Object Identifier: 10.3969/j.issn.1674-862X.2014.03.017
 Journal of Electronic Science and Technology2014年3期
Journal of Electronic Science and Technology2014年3期
- Journal of Electronic Science and Technology的其它文章
- Detecting Circles Using a Two-Stage Approach
- Weighted Learning for Feedforward Neural Networks
- Performance Evaluation of Mobility Anchor Point with Guard Load Reservation in Hierarchical Mobile IPv6
- A Path-Based Approach for Data Aggregation in Grid-Based Wireless Sensor Networks
- Role of Gate in Triode-Structure for Carbon Nanotube Cold Cathode
- Object Tracking Using a Particle Filter with SURF Feature
