Performance Evaluation of Mobility Anchor Point with Guard Load Reservation in Hierarchical Mobile IPv6
Yung-Chung Wang, Li-Hsin Chiang, and Hung-Pin Lin
Performance Evaluation of Mobility Anchor Point with Guard Load Reservation in Hierarchical Mobile IPv6
Yung-Chung Wang, Li-Hsin Chiang, and Hung-Pin Lin
—Hierarchical mobile IPv6 (HMIPv6) introduces a mobility anchor point to reduce the signaling overhead and handoff latency. In this paper, we apply the matrix-analytical approach to explore the performance measures of the ongoing mobile nodes (MNs) drop and new MNs block probabilities of mobility anchor point with a guard bandwidth reservation scheme. We apply the Markovian arrival process (MAP) to model ongoing MNs and new MNs. Five related performance measures are derived, including the long-term new MN block and ongoing MN drop probabilities, and the three short-term measures of average length of a block period and a non-block period, as well as the conditional ongoing MN drop probability during a block period. These performance measures greatly assist the guard bandwidth reservation mechanism in determining a proper threshold guard bandwidth. The results presented in this paper can provide guidelines for designing adaptive algorithms to adjust the threshold in the guard bandwidth reservation scheme.
Index Terms—Hierarchical mobile IPv6, Markovian arrival process, matrix-analytic method, mobility anchor point.
1. Introduction
With the increasing number of wireless network infrastructure deployment and the popularity of portable computing devices such as the smart phone, tablet PC, and notebook computer, more and more Internet users are experiencing ubiquitous mobility using both these computing devices and the wireless networks to access the Internet. According to this growth, the applications in the wired Internet, such as web browsing, voice over IP (VoIP), and teleconference, are moving gradually toward the mobile wireless environment. Therefore, it is necessary to develop the mobility support protocol in Internet. Mobile IPv6 (MIPv6)[1]is the mobility support protocol in Internet. In MIPv6, the home agent (HA) not only handles binding update (BU) requests pertaining to intra-domain handoffs, but also performs packet encapsulation originated from the mobile nodes (MNs), which would cause the traffic to place a burden on the entire network. To reduce above problem in MIPv6 when MNs perform frequent handoffs, hierarchical mobile IPv6 (HMIPv6)[2]introduces the concept of a mobility anchor point. The mobility anchor point handles BU requests pertaining to intra-domain handoffs in a localized manner. Therefore, the mobility anchor point not only handles binding updates, but also performs packet encapsulation originated from the MNs. As the number of MNs serviced by a mobility anchor point increases, the mobility anchor point suffers from traffic overload, which results in providing lower quality of service for applications. Therefore, the performance evaluation of traffic load control at the mobility anchor point is one of the most crucial issues.
Handoff basically involves the change of resources from one mobility anchor point to an adjacent mobility anchor point. It is well known that if a new MN is blocked, it is not as disastrous as a handoff MN being dropped. Therefore, it is important to provide a higher priority to handoff MNs so that ongoing MNs can be maintained. One way of assigning the priority to handoff requests is to assign the guard bandwidth to be used exclusively for handoff MNs from among the resources in a mobility anchor point. This guard bandwidth reservation handoff scheme has a tunable threshold for guard bandwidth configuration. With a selected threshold, a block period is defined as the interval of time during which the MNs in a mobility anchor point is at or above the threshold value, and a non-block period is the complementary interval of time. The available capacities at or below the threshold is shared by new MNs and handoff MNs. Arriving new MNs are blocked by the control scheme during a block period. Handoff MNs are dropped only when the capacity is full.
Choosing an appropriate threshold for the guard bandwidth for handoff MNs is the most significant design issue for HMIPv6. If a relatively low threshold is chosen, new MNs will be excessively blocked, causing a low utilization of the capacity in a mobility anchor point. On the other hand, if a fairly high threshold is chosen, handoff MNs will be dropped more than expected because of theoccupancy of the capacity by new MNs. This phenomenon prevents the system from being able to meet the required drop probability for handoff MNs. Hence, the threshold setting is a trade-off between the system utilization and the guaranteed drop probability for handoff MNs. The performance analysis of a threshold policy is therefore necessary and desirable in order to assist the system in choosing a proper threshold.
The guard load reservation handoff scheme has increasingly been receiving attention in HMIPv6 design due to its simplicity in the implementation. Several performance evaluations have been conducted by examining the new MN block and handoff MN drop behavior of a mobility anchor point with a guard load reservation scheme[3]. This paper considers only the Poisson new and handoff MN arrival process case. However, there is significant evidence that the new and handoff MN traffic cannot always be modeled as a Poisson process. In this paper, we use a Markovian arrival process (MAP) to model handoff MN arrival processes due to the following conditions: 1) it is simple but good enough to fit field data, and 2) the resulting queueing system model is tractable. A main advantage of using Markovian models for traffic description of queues is that there are efficient numerical analysis methods, commonly referred to as matrix analytic methods, for the evaluation of a Markovian queue. However, although the MAP requires the estimation of a large number of parameters to describe the network traffic[4], much research has focused on parameter estimation and applications of MAP to model network traffic. Buchholz[5]presented an algorithm to fit the parameters of MAP according to measured data. In [6], Heyman and Lucantoni provided the evidence that the Markov-modulated Poisson process (MMPP) which is a special case of MAP is a good model for Internet traffic at the packet/byte level. In [7], Kanget al. provided the evidence that MAP yielded a very good estimation of the cell loss ratio for common super positions of voice and VBR video sources. In [8], Salvadoret al. proposed a parameter fitting procedure using superposed two-state MMPP that leads to accurate estimates of queueing behavior for network traffic exhibiting long-range dependent behavior. Telek[9]derived the minimal presentation of MAP and developed effective fitting models. Based on those studies, we can state that the MAP process is able to model a wide variety of new and handoff MN arrival.
In addition to the evaluation of the new MN block and handoff MN drop probabilities, we examine the conditional handoff MN drop during the block period. The threshold used to determine the block period splits the state space in two, allowing the use of two hypothesized Markov chains to describe the alternating renewal process. The distributions of various absorbing times in the two hypothesized Markov chains are derived to compute the average durations of the block period and the conditional handoff MN drop probability during a block period. These performance measures will significantly assist the guard bandwidth reservation handoff mechanism for determining a proper threshold. The overall analysis in this paper is based on the matrix-analytic approach[10],[11]. It is simple and efficient to compute the numerical results by any efficient mathematical tool.
This paper is organized as follows. In Section 2, the HMIPv6 network is briefly introduced. In Section 3, the MAP as the new and handoff MN model is introduced in brief. In Section 4, the new MN block probability and handoff MN drop probability are analyzed. Numerical results are computed and discussed in Section5 to reveal the computational tractability of our analysis and to gain insight into the design of a guard load reservation handoff scheme in HMIPv6 networks. Some concluding remarks are given in Section 6.
2. Hierarchical Mobile IPv6
Hierarchical mobile IPv6 (HMIPv6) is a localized mobility management proposal that aims to reduce the signaling load due to user mobility. The mobility management inside the local domain is handled by a mobility anchor point. Mobility between separate mobility anchor point domains is handled by MIPv6.
The mobility anchor point basically acts as a local home agent. When a mobile node enters into a new mobility anchor point domain, it registers with it obtaining a regional care-of address (RCoA). The RCoA is the address that the mobile node will use to inform its home agent and correspondent nodes about its current location. Then, the packets will be sent to and intercepted by the mobility anchor point, acting as a proxy, and routed inside the domain to the on-link care-of address (LCoA). Once the MN has successfully registered with the mobility anchor point, a bi-directional tunnel is established between them. All packets sent by the MN are tunneled to the mobility anchor point. All packets addressed to the MN’s RCoA are intercepted by the mobility anchor point and tunneled to the MN’s LCoA. If the MN changes its current address within the same mobility anchor point domain, it only needs to register the new LCoA with the mobility anchor point. The RCoA does not change as long as the MN moves within the same mobility anchor point domain. This makes the MN’s mobility transparent to the CNs.
In this paper, we focus on the guard load reservation at the mobility anchor point and consider that there is only one mobility anchor point available to each MN. The mobility anchor point capacityCis represented by the maximum number of MNs that it can service. First, an MN sends a local BU message to the mobility anchor point. If the BU message is accepted by the mobility anchor point, the MN will receive a successful back message and then send a BU message with its RCoA to the HA. On the other hand, the MN’s BU message is rejected by the mobility anchor point, the rejected MN registers its LCoA with the HA and then the packets destined for the MN will bypassthe mobility anchor point. Regarding route optimization, if the local BU message is accepted, the MN’s RCoA is notified to the CNs. Otherwise, the MN’s LCoA is sent to the CNs.
When a BU message arrives at a mobility anchor point, the mobility anchor point triggers the threshold-based admission control algorithm. LetCthbe a pre-defined threshold. When the number of MNs serviced by the mobility anchor point is less thanCth, both new MNs and ongoing MNs are admitted. On the other hand, to give a higher priority to ongoing MNs, when the current mobility anchor point load is equal to or greater thanCth, only ongoing MNs are accepted. This threshold-based admission control algorithm reduces the ongoing MN dropping probability at the cost of increasing the new MN blocking probability.
3. Traffic Model
Many analytically tractable models have been proposed to describe new MNs and handoff MN arrivals in the literature. In this paper, the arrival process of new and handoff MNs is modeled by a MAP. A brief exposition of MAP is given in the rest of this section.
The MAP is a generalization of the Poisson arrival process by allowing for non-exponential inter-arrival times, while still preserving an underlying Markovian structure[12]. It is a marked point process with arrivals generated at the transition epochs of a particular type ofm-state Markov renewal process[13]. A MAP can be more easily described by a two-dimensional continuous-time Markov chain {(N(t),J(t)),t≥0} on the state space {(n,j)|n≥0, 1≤j≤m}, with a infinitesimal generatorQMAP, having the structure:
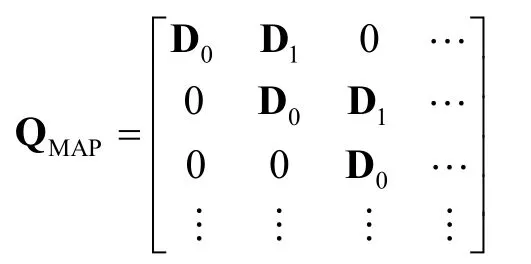
whereN(t) stands for a counting variable,J(t) represents an auxiliary phase variable, andDkarem×mmatrices, called parameter matrices. The Markov chain then defines an arrival process where the transition from state (n,i) to state (n+1,j), n≥0, and 1≤,i j≤m, corresponds to an arrival and a phase change from phaseito phasej. The matrixD1with elements (D1)i,j, 1≤,i j≤m, governs the state transitions which correspond to an arrival, and the matrixD0governs the state transitions which correspond to no arrivals. The sum of both parameter matrices is

which is the infinitesimal generator of the underlying Markovian structure {J(t),t>0} with respect to the MAP. We assume that the underlying Markovian structure is stable and irreducible. Thus the Markov chain {J(t),t> 0} has a unique stationary probability vector π, and
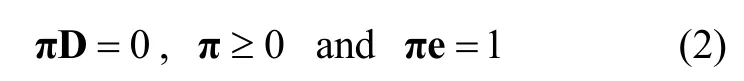
whereeis assumed in this paper to be an all-1 column vector with a compatible dimension. We also assume thatD0is nonsingular such that the sojourn time at any state of the state space {(n,j)|n≥ 0, 1≤j≤m} is finite with probability 1, for guaranteeing that the process never terminates. The fundamental arrival rate λ of this MAP is defined as

In this paper, we propose to model both new and handoff MN by a MAP. We assume that the new MN is characterized by a sequenceof parameter matrices and the handoff MN by a sequenceof parameter matrices.aremn×mnandmh×mhmatrices, respectively. The sequenceof the defining parameter matrices for the superposed new and handoff MN can be obtained by
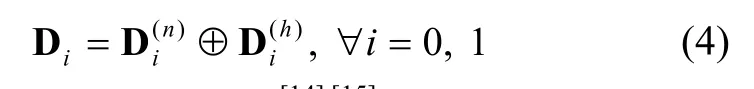
where ⊕ is the Kronecker sum[14],[15]. Note that eachDihas the dimensions of (mnmh)×(mnmh)[13].
4. Performance Analysis
The new arrival MN will be modeled by using a MAP with a sequenceand the handoff MN will be modeled by using a MAP with a sequenceas described in Section 3. We assume that the ongoing MN (new or handoff) connection times are exponentially distributed with parameter μc. The time spent in a given mobility anchor point, before handing off, is also exponentially distributed with parameter μd. Note that new MNs which find allCthcapacity will leave the system and handoff the MNs which find allCcapacity busy will leave the system.
4.1 Queueing Model
Consider the embedded continuous-time Markov chain {(L(t),J(t)),t≥0} of the queuing system on the twodimensional state space ({0, 1, …,C}×{(1, 1), (1, 2), …, (mn,mh)}), whereL(t), andJ(t) denote the capacity occupancy, and the phase of the underlying MAP of superposition of handoff MN and new MN at timet, respectively. For convenience, the queuing system is said to be at a leveljif its capacity occupancy is equal toj. The embedded Markov chain now has an infinitesimal generatorQof the following block form:

4.2 New MN Block and Handoff MN Drop
Probabilities
Letx=(x0,x1, …,xC) be the stationary probability vector of the Markov chainQ, i.e.,
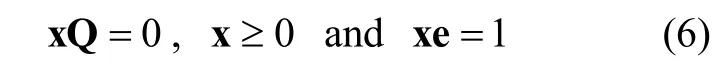
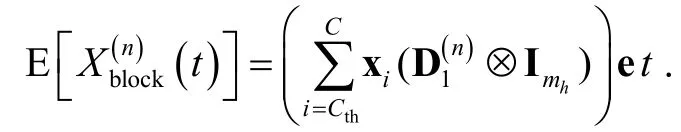
Consequently, the new MN blocking probability, denoted bycan be calculated by

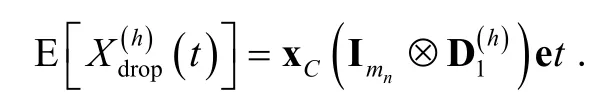
Consequently, the handoff MN dropping probability, denoted bycan be calculated by
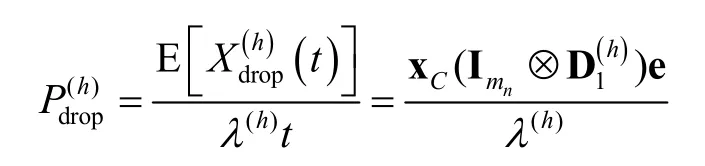
4.3 Distribution of Block and Non-Block Periods
The queueing system passes through alternating block and non-block periods. The patterns of block and non-block periods are then studied by decomposing the state spaceSinto two subsets, i.e.,according to the block thresholdCth. With this partition of the state space, the infinitesimal generatorQof the embedded Markov chain of the queuing system can be partitioned as
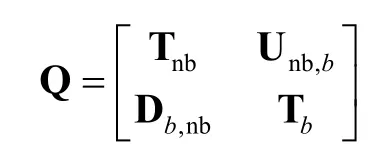
where

where matricesTnb,Unb,b,Tb, andDb,nbare transition rate sub-matrices governing transitions fromSnbinto itself, fromSnbintoSb, fromSbinto itself, and fromSbintoSnb, respectively. The sojourn time in each non-block period and block period is characterized by a transient Markov chain, with respect toTnbandTbfor transitions onSnbandSb.

Next, non-block and block periods are characterized by deriving the steady state probabilities for the initial state of each transient Markov chain, as denoted by vector αnbfor non-block periodes and vector αbfor block periods, defined byLetLnbandLbbe the lengths of non-block and block periods, respectively. Obviously,LnbandLbare the life times of the two transient Markov chains, with respect toTnbandTbfor transitions onSnbandSb. Thus,fnb(t) andfb(t) represents the probability density functions of all absorbing times of the transient Markov chains, with respect toTnbandTbfor transitions onSnbandSb. According to the transient Markov chain theory, the Laplace transforms offnbandfbare
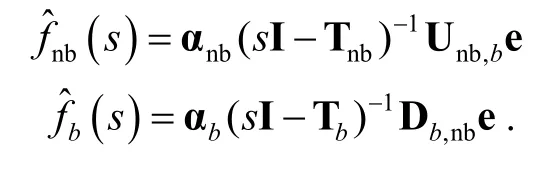
The average lengths of non-block and block periods are

4.4 Handoff MN Drop Probability during a Block Period
To investigate the drop behavior during a block period, the sub-matrixTbis written as

where

where the matrixTb(h)(0) comprises the probabilities that make state transitions withinSbwithout any handoff MN drops. However, the matrixTb(h)(1), comprises the probabilities that make state transitions withinSbwith a handoff MN drop.
Notably, the behavior of the queuing system during a block period can be described by the transient Markov chain,Tbfor transitions onSb. For a state (i, (jn,jh)) inSb, letbe the probability that the state of transient Markov process enters (i, (jn,jh)) with a total oflhandoff MNs dropped during [0,t). Letbe an |Sb|-vector whose (i, (jn,jh))-th element isThe vectort>0,l≥0, can be obtained by the differential equation:
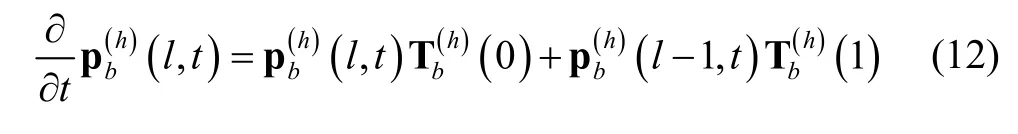
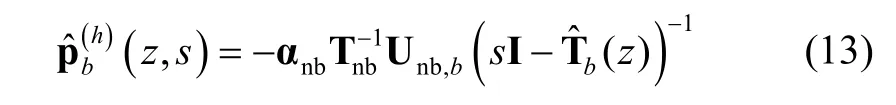

Now the average total number of MN drops during a block period, denotedcan be calculated as
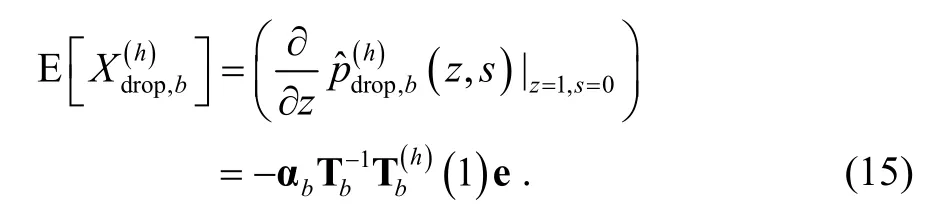
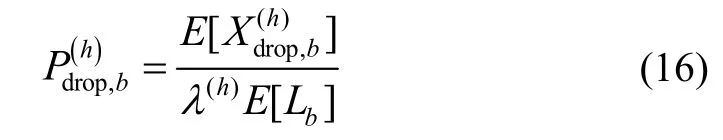
where E[Lb] is the average length of a block period in (11) and()h
λ is the fundamental arrival rate of the handoff MN and can be calculated by (3).
5. Numerical Results and Discussion
In this section, we will investigate the numerical results under the MAP new MN and handoff MN. In our experiments, the numerical values of the MAP parameters of the handoff MN are

and the numerical values of the MAP parameters of the new MN are


[1] D. Johnson, C. Perkins, and J. Arkko. (June 2003). Mobility support inIPv6. IETF RFC 3775. [Online]. Available: http://www.ietf.org/rfc/rfc3775.txt
[2] H. Soliman, C. Castelluccia, K. E. Malki, and L. Bellier. (August 2005). Hierarchical mobile IPv6 mobility management (HMIPv6). IETFRFC 4140. [Online]. Available: http://tools.ietf.org/html/rfc4140
[3] S. Pack, T. Kwon, and Y. Choi, “A mobility-based load control scheme in hierarchical mobile IPv6 networks,”Wireless Networks, vol. 16, no. 2, pp. 545-558, 2010.
[4] M. Iftikhar, T. Singh, B. Landfeldt, and M. Caglar,“Multiclass G/M/1queueing system with self-similar input and non-preemptive priority,” Computer Communications, vol. 31, no. 5, pp. 1012-1027, 2008.
[5] P. Buchholz, “An EM-algorithm for MAP fitting from real traffic data,” Computer Performance Evaluation Modelling Techniques and Tools, LNCS, vol. 2794, pp. 218-236, 2003.
[6] D. P. Heyman and D. Lucantoni, “Modeling multiple IP traffic streams with rate limits,” IEEE/ACM Trans. on Networking, vol. 11, no. 6, pp. 948-958, 2003.
[7] S. H. Kang, Y. H. Kim, D. K. Sung, and B. D. Choi, “An application of Markovian arrival process (MAP) to modeling superposed ATM cell streams,” IEEE Trans. on Commun., vol. 50, no. 4, pp. 633-642, 2002.
[8] P. Salvador, R. Valadas, and A. Pacheco, “Multiscale fitting procedure using Markov modulated Poisson processes,”Telecommunication Systems, vol. 23, no.1-2, pp. 123-148, 2003.
[9] M. Telek and G. Horvath, “A minimal representation of Markov arrival processes and a moments matching method,”Performance Evaluation, vol. 64, pp. 1153-1168, Oct. 2007.
[10] M. F. Neuts, Matrix-Geometric Solutions in Stochastic Models—An Algorithmic Approach, London: The Johns Hopkins University Press, 1981.
[11] M. F. Neuts, Structured Stochastic Matrices of M/G/1 Type and Their Applications, New York: Marcel Dekker, 1989.
[12] D. M. Lucantoni, “New results on the single server queue with a batch Markovian arrival process,” Commun. Statist. Stochastic Models, vol. 7, no. 1, pp. 1-46, 1991.
[13] M. F. Neuts, “Models based on the Markovian arrival process,” IEICE Trans. Commun., vol. E75-B, no. 12, pp. 1255-1265, 1992.
[14] R. Bellman, Introduction to Matrix Analysis, 2nd ed. New York: McGraw-Hill, 1970.
[15] A. Graham, Kronecker Products and Matrix Calculus with Applications, New York: Horwood Halsted Press, 1981.
[16] M. Schwartz, Mobile Wireless Communications. Cambridge: Cambridge University Press, 2005.

Yung-Chung Wangwas born in Taiwan in 1963. He received the M.S. and Ph.D. degrees in electrical engineering from National Tsing Hua University, Hsinchu in 1990 and 2000, respectively. From 1990 to 2001, he was a research engineer with the Chung-Hwa Tele-Communication Lab.,
where he was engaged in research on the development of ATM switching systems and IP switch router systems. Since 2001, he has been with the Department of Electrical Engineering, National Taipei University of Technology (TaipeiTech), Taipei, where he is a full professor. His research interests include wireless networks, optical networks, software defined networks, and queuing theory and performance evaluation of communication networks.

Li-Hsin Chiangwas born in Taiwan in 1965. He received the M.S. degree in computer science and information engineering from TaipeiTech, Taipei in 2004. He is currently pursuing the Ph.D. degree with the Department of Electrical Engineering, TaipeiTech. His research interests include computer network, admission control, and Internet applications.

Hung-Pin Linreceived his M.S. degree in electrical engineering from TaipeiTech in 2008. He is currently a Ph.D. student with the Department of Electrical Engineering, TaipeiTech. His research interests include media streaming, web, and mobile application architectures.
Manuscript received December 12, 2013; revised March 10, 2014.
Y.-C. Wang is with the Department of Electrical Engineering, National Taipei University of Technology, Taipei 10608 (Corresponding author e-mail: ycwang@ntut.edu.tw).
L.-H. Chiang and H.-P. Lin are with the Department of Electrical Engineering, National Taipei University of Technology, Taipei 10608 (e-mail: romeo@ntut.edu.tw; t7319014@ntut.edu.tw).
Color versions of one or more of the figures in this paper are available online at http://www.journal.uestc.edu.cn.
Digital Object Identifier: 10.3969/j.issn.1674-862X.2014.03.012
 Journal of Electronic Science and Technology2014年3期
Journal of Electronic Science and Technology2014年3期
- Journal of Electronic Science and Technology的其它文章
- A High Efficiency Fully Integrated OOK Transmitter for WBAN
- Weighted Learning for Feedforward Neural Networks
- A Path-Based Approach for Data Aggregation in Grid-Based Wireless Sensor Networks
- Detecting Circles Using a Two-Stage Approach
- Numerical Solution for Fractional Partial Differential Equation with Bernstein Polynomials
- Object Tracking Using a Particle Filter with SURF Feature
