多级步长光伏电池最大功率点跟踪

王 平，卞建龙

（河海大学能源与电气学院，南京211100）

光伏电池的输出特性[1]受外界环境的影响较大，效率较低。研究太阳能电池的模型及其最大功率点跟踪策略MPPT（maxiumum power point tracking），对于光伏电池转换效率[2]的提高有着重要的意义。针对MPPT 的问题，学者们提出了很多MPPT 算法。其中比较原始的是恒定电压和恒定电流法，这两种算法虽实现最简单，但控制性能最差；基于模糊控制和神经网络的智能控制算法应用也比较多，但是实现起来较为复杂，需要占用控制器的大量资源，降低控制器运行速度，控制成本高；近年来，国内外学者开始研究采用粒子群算法进行最大功率点跟踪[3～4]，虽然这种算法能有效运用于分布式的光伏发电以及复杂的多峰情况，但对于单个的光伏组件，其要求建模的精度较高，并且在外界环境变化的时候需要重启算法。至于工程上应用较多的功率扰动法P&O（perturbation and observation methold）与电导增量法[5]，因其算法性价比高而备受青睐，而这两种算法同时存在跟踪速度与跟踪精度不能很好兼顾的问题。一些学者也试着使用最优梯度法或自适应变步长法[6～7]在线实时调整跟踪步长，能够兼顾到速度与精度的要求，但是存在步长因子难以选择最优的问题，并且要求采样器有足够高的精度，有时会由于电力电子器件的纹波导致得到的步长很大，以致算法无法跟踪到最大功率点，在工程上较难实现。

在权衡控制性能和经济成本的基础上，本文参考了文献[8]的自适应占空比扰动法，此方法采用了两级步长跟踪，虽兼顾了跟踪速度和精度，但是从动态跟踪到稳态运行不能较平滑地过渡，在接近稳态运行点时存在较大振荡，而且在稳态运行时虽然使用较小的步长，但输出的功率仍然存在波动。本文在此基础上，增加了步长的级数，使系统跟踪到最大功率点附近时振荡减小，跟踪过程变得更为平稳；在跟踪到较高的精度时设定零步长扰动，保证系统在稳态运行时无振荡，并且此方法针对提出的控制性能（速度和精度）要求，确保了一定的跟踪裕量，包括速度裕量和精度裕量，以保证跟踪的可靠性。

1 光伏电池特性与建模仿真

1.1 光伏电池特性

光伏电池原理[9～10]如图1 所示，因并联电阻Rsh很大、串联电阻Rs很小，其近似等效伏安特性方程为

式中：Iph为光电流；Id为暗电流；Io为反向饱和电流；q 为电子电荷，1.6×1019C；K 为玻尔兹曼常数，1.38×10-23J/K；n 为二极管因子；T 为摄氏温度。

图1 光伏电池原理Fig.1 Schematic diagram of PV cell

1.2 光伏电池的数学建模与特性曲线

光伏电池在标准条件下测试得到的4 个重要技术参数为：短路电流Isc、开路电压Voc、最大功率点电流Im和最大功率点电压Vm。为了便于建立工程用的模型（误差6%以内[11]），令Isc≈Iph，得到简化的伏安特性方程[12]，即

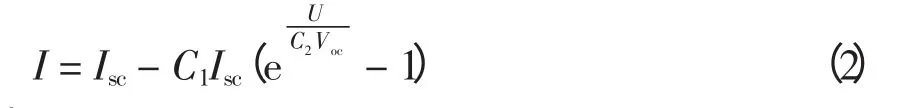
其中：

则C1、C2的表达式[10]为

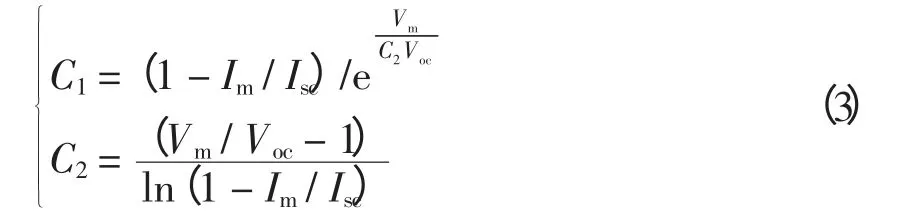
文献[11]的第1 种方法建立的光伏电池数学模型，只能通过给定标准测试条件的（U，I）点修正得到在新的日照和温度下的（Unew，Inew）点，不便于用来做最大功率点跟踪的仿真。而文献[11]的第2种方法是根据标准测试条件下的Isc、Voc、Im、Vm，推算出新的条件下的Isc_new、Voc_new、Im_new、Vm_new，再代入式（3）得出C1、C2，最后代入式（1）得出伏安特性方程，极大地方便了最大功率点跟踪的仿真。

140 W 光伏电池模块的技术参数见表1。采用文献[11]第2 种方法仿真得到不同光照下的I-U曲线、P-U 曲线，分别如图2、图3 所示。

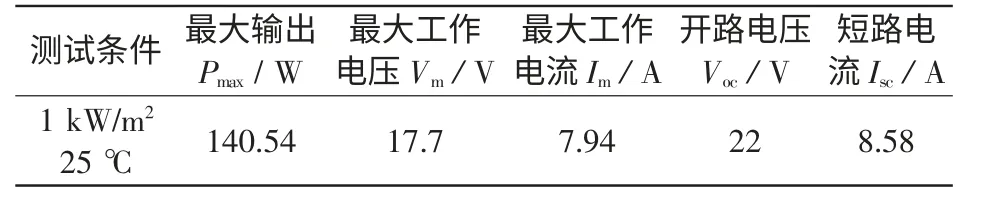
表1 140 W 光伏电池的技术参数Tab.1 Technical parameters of 140 W PV cell

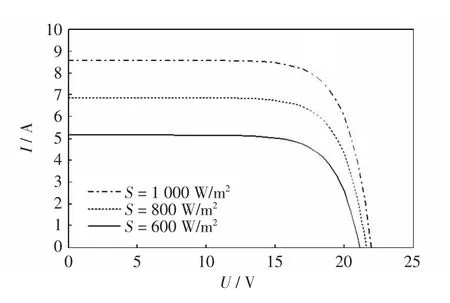
图2 不同光照下的I-U 曲线Fig.2 I-U curves under different illumination

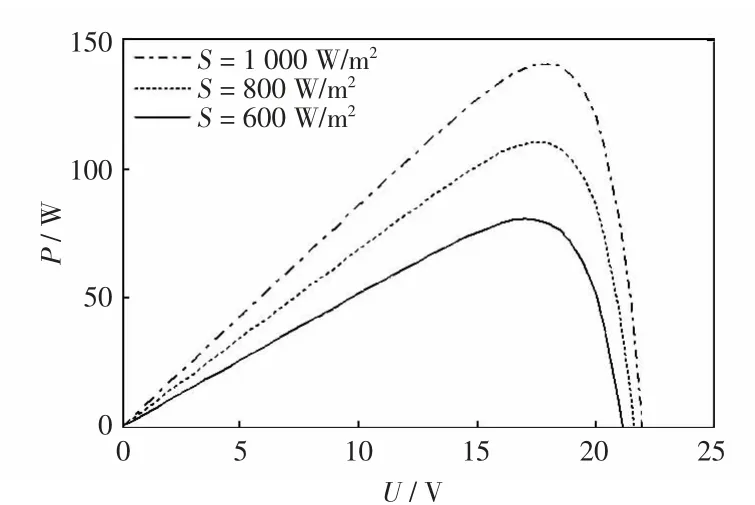
图3 不同光照下的P-U 曲线Fig.3 P-U curves under different illumination

2 MPPT 算法的改进

2.1 MPPT

从以上仿真结果可以看出，光伏电池的伏安特性本身具有非线性，且其伏安特性受外界环境的影响很大，所以光伏电池是一个很不稳定的非线性电源。MPPT 控制是一个自寻优的过程，即通过控制光伏电池的端电压来使光伏电池在环境（日照、温度）变化时，智能化地输出最大功率[13]。一般在负载与光伏电池之间增加一个DC/DC 变换器，通过采用这些算法来改变变换器的导通率，使光伏电池工作在最大功率点。

2.2 MPPT 的系统结构

MPPT 的系统结构如图4 所示，系统由主电路与Boost 控制部分构成。主电路部分由光伏电池、Boost 电路以及负载这3 部分组成；Boost 控制部分是通过调节占空比来控制PWM 电路的输出脉冲，用脉冲控制Boost 电路中的开关，从而调节光伏电池的输出电压U，实现MPPT 的功能。

图4 最大功率点跟踪系统结构Fig.4 Structure of MPPT system

2.3 固定步长占空比扰动法

本文采用将占空比D 作为控制参数即占空比扰动法[14]，最终达到阻抗匹配[8]，实现MPPT。占空比扰动法本质上与功率扰动法P&O 没有区别，其算法流程如图5 所示。

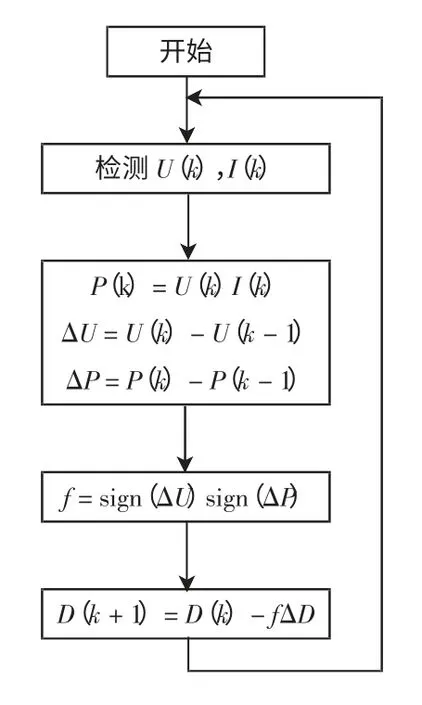
图5 固定步长扰动观察法流程Fig.5 Flow chart of fixed step-size P&O method

对表1 的太阳能电池参数（负载电阻R=20 Ω）进行最大功率点跟踪仿真。当光照度S 为1 kW/m2、太阳能电池的温度T 为25 ℃时，选取步长ΔD=0.000 01，得到MPPT 的仿真曲线如图6（a）所示。此时虽然能够精确地跟踪最大功率点，但跟踪速度相对较慢。

在同样条件下，选取固定步长ΔD=0.000 1，得到的最大功率跟踪的仿真曲线如图6（b）所示。此时跟踪速度虽然大大提高，但在到达最大功率点附近后，输出功率存在较大的振荡，造成很多的能量损失。从以上2 种仿真结果可以看出，固定步长法不能兼顾到系统最大功率跟踪的速度和精度。

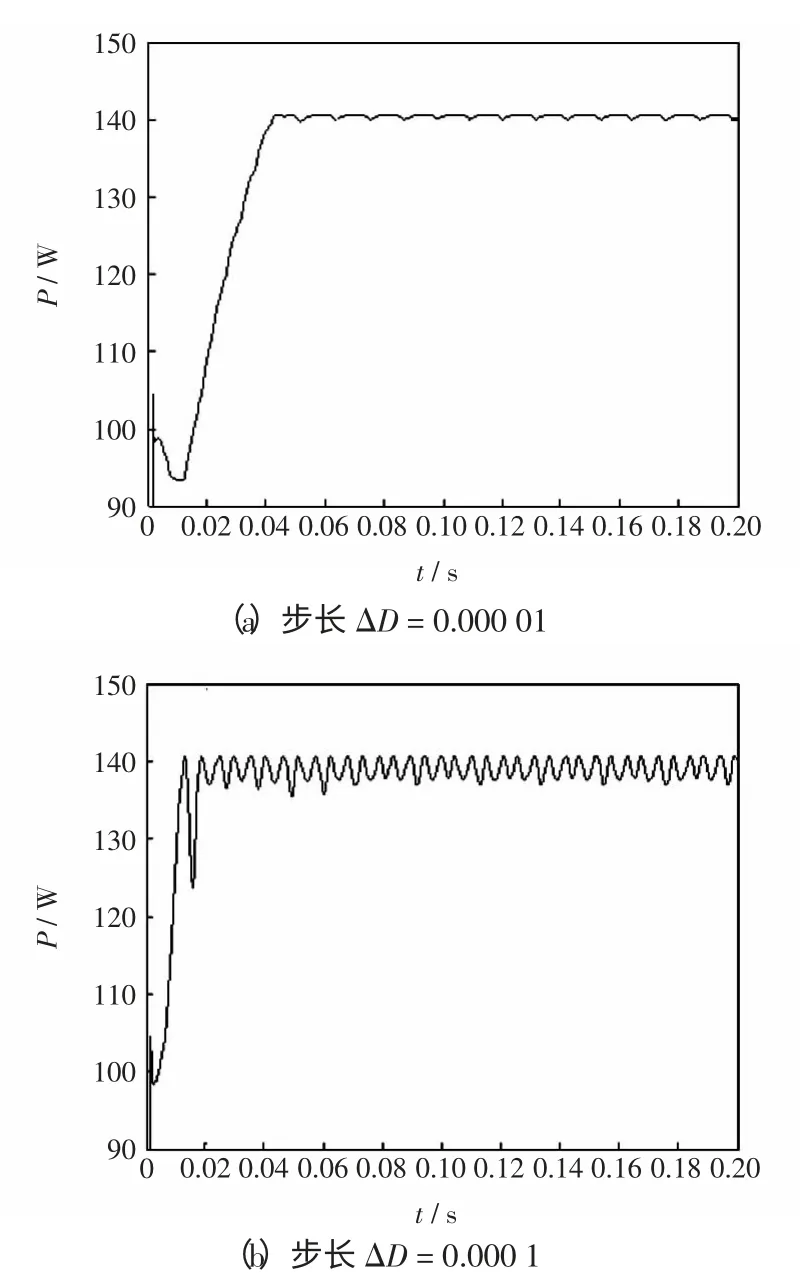
图6 固定步长的MPPT 仿真Fig.6 MPPT simulation with fixed step-size

2.4 二级步长占空比扰动法

在实际工程中，一般对控制精度与控制速度都有相应的要求，若要求控制精度达到图6（a）的要求，控制精度达到图6（b）的要求，此时若采用固定步长的占空比扰动法则不能同时满足要求。

文献[8]针对这个问题使用这2 个步长进行跟踪的方法，也就是两级步长跟踪方法。在离最大功率点较远处采取用大步长，即采用图6（b）的跟踪步长跟踪到最大功率点附近，以加快跟踪速度；然后在离最大功率点较近处，采用小步长，即采用图6（a）的步长扰动，使系统稳定运行在最大功率点附近，并且系统以较小的振幅振荡运行。在与固定步长同样的仿真条件下，采取两级步长得到仿真结果如图7 所示。

由仿真结果可知：这种方法虽兼顾了跟踪速度与精度，但是从动态快速跟踪到稳态运行，不能较平滑地过渡，在这个过渡期会有较大的振荡，且稳定运行时输出功率仍然存在振荡问题。

2.5 多级步长占空比扰动法

针对两级步长的跟踪问题本文设计了多级步长的跟踪策略，如图8 所示，且设定了稳定运行时停止扰动的策略，以保证系统较为平滑地过渡，且使稳定运行时功率输出无振荡。

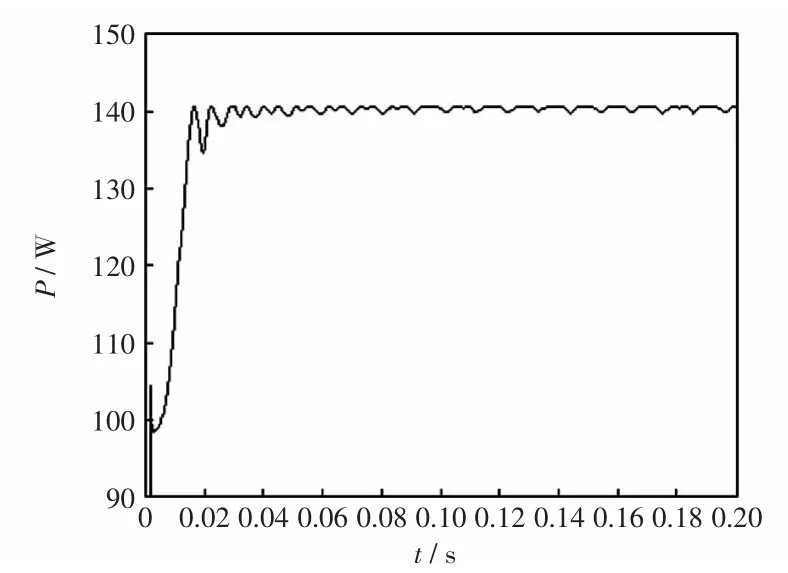
图7 两级步长MPPT 仿真Fig.7 MPPT simulation with two step-sizes

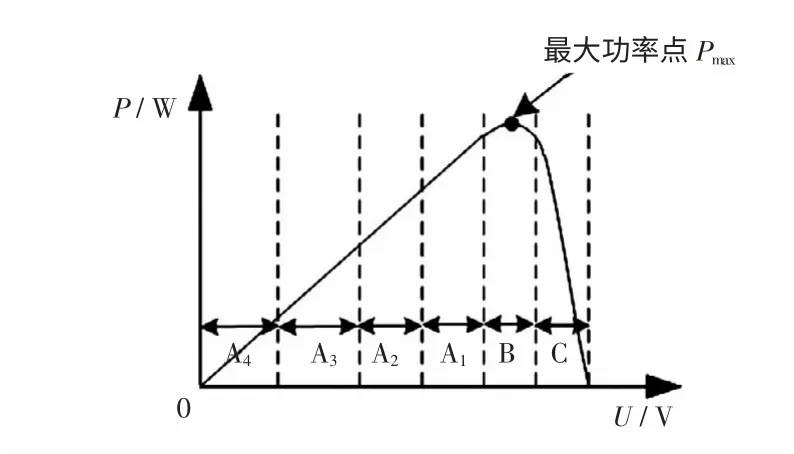
图8 多级步长的原理示意Fig.8 Schematic diagram of multiple step-sizes

为了使系统过渡平稳，减小跟踪过程中的振荡，在原有步长为0.000 01 和0.000 1 两个数量级的基础上增加了2 个数量级，分别为0.000 001 和0.001。为了使系统稳定运行时无振荡，在此基础上又增加了零扰动步长的设定。

步长ΔD 随ξ 的变化而有级地进行变化，ξ 的表达式为

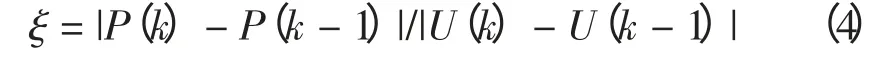
步长ΔD 的取值如表2 所示。

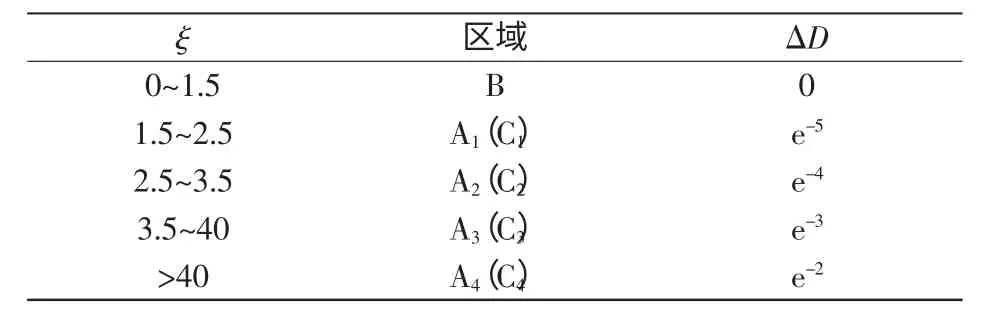
表2 ΔD 取值Tab.2 Value of ΔD

在与两级步长法同样的仿真条件下，采取多级步长法得到的仿真结果如图9 所示。与两级步长法所得到的仿真结果比较可以看出，在一定的光照和温度下，本文改进的多级步长法不仅能平稳地跟踪到最大功率点，稳定运行时输出功率恒定，不存在振荡的情况，而且比原先的跟踪速度更快，稳态逼近精度更高。在外界光照条件发生改变（800→600→1 000）的情况下，得到如图10 所示的多级步长MPPT 仿真曲线。可见在光照强度发生变化时，此算法仍然能够快速且准确地实现最大功率点跟踪。

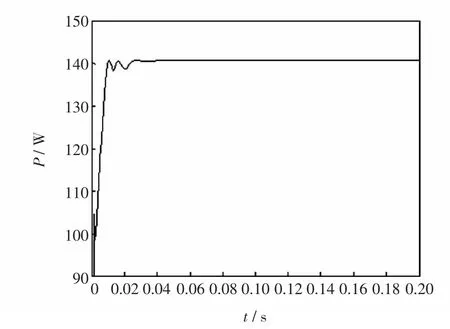
图9 多级步长MPPT 仿真Fig.9 MPPT simulation with multiple step-size

图10 照度变化时多级步长MPPT 仿真Fig.10 MPPT simulation with multiple step-size under changing illumination

3 结论

本文通过对光伏电池原理的分析建模，仿真研究了不同照度下光伏电池的特性。对固定步长的占空比扰动法进行了仿真，并针对固定步长法不能同时兼顾跟踪速度与精度的问题，参照文献[8]的两级步长最大功率点跟踪方法进行改进，提出了一种实现方便的多级步长控制策略。仿真结果表明该控制策略不仅能同时满足了跟踪速度和精度的要求，在环境快速变化的情况下能快速、准确地跟踪到最大功率点，而且还有3 点改进：

（1）从快速跟踪到稳定运行的控制过程变得更为平稳，跟踪过程中振荡减小；

（2）跟踪精度有所提高，并且在稳定运行时系统功率输出无振荡；

（3）能针对相应提出的控制性能要求，确保一定的跟踪裕量，包括速度裕量和精度裕量，更容易满足工程中跟踪可靠性的要求。

[1]赵福鑫，魏彦章.太阳电池及其应用[M].北京：国防工业出版社，1985.

[2]OMANH. Space solar power development [J]. IEEEAES Systems Magazine，2000，15（2）：3-8.

[3]朱艳伟，石新春，但扬清，等（Zhu Yanwei，Shi Xinchun，Dan Yangqing，et al）. 粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用（Application of PSO algorithm in global MPPT for PV array）[J]. 中国电机工程学报（Proceedings of the CSEE），2012，32（4）：42-48，S6.

[4]Kamejima T，Phimmasone V，Kondo Y，et al. The optimization of control parameters of PSO based MPPT for photovoltaics[C]//IEEE Ninth International Conference on Power Electronics and Drive Systems.Singapore：2011.

[5]王长贵，王斯成.太阳能光伏发电实用技术[M].北京：化学工业出版社，2005.

[6]黄舒予，牟龙华，石林（Huang Shuyu，Mu Longhua，Shi Lin）.自适应变步长MPPT 算法（Adaptive variable step size MPPT algorithm）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（5）：26-30.

[7]王厦楠（Wang Xianan）.独立光伏发电系统及其MPPT的研究（The Research of the Stand-Alone Photovoltaic System and It’s Maximum Power Point Tracking）[D]. 南京：南京航空航天大学民航学院（Nanjing：College of Civil Aviation，Nanjing University of Aeronautics and Astronautics），2008.

[8]曹金虎，薛士龙，陈意惠，等（Cao Jinhu，Xue Shilong，Chen Yihui，et al）.基于自适应占空比扰动的MPPT 算法研究（MPPT algorithm research on the basis of selfadaptive duty cycle disturbance）[J].佳木斯大学学报（自然科学版）（Journal of Jiamusi University（Natural Science Edition）），2011，29（1）：76-79，85.

[9]冯垛生，宋金莲，赵慧，等.太阳能发电原理与应用[M].北京：人民邮电出版社，2007.

[10]王长江（Wang Changjiang）.基于MATLAB 的光伏电池通用数学模型（Versatile model for photovoltaic cell based on MATLAB）[J].电力科学与工程（Electric Power Science and Engineering），2009，25（4）：11-14.

[11]苏建徽，余世杰，赵为，等（Su Jianhui，Yu Shijie，Zhao Wei，et al）.硅太阳电池工程用数学模型（Investigation on engineering analytical model of silicon solar cells）[J].太阳能学报（Acta Energiae Solaris Sinica），2001，22（4）：409-412.

[12]赵争鸣.太阳能光伏发电及其应用[M].北京：科学出版社，2005.

[13]赵为（Zhao Wei）. 太阳能光伏并网发电系统的研究（Research on Grid-Connected Photovoltaic System）[D].合肥：合肥工业大学电气与自动化工程学院（Hefei：School of Electrical Engineering and Automation，Hefei University of Technology），2003.

[14]杨文杰（Yang Wenjie）.光伏发电并网与微网运行控制仿真研究（Simulation and Research of Grid Connected Photovoltaic Generation and Microgrid Operation Control）[D].成都：西南交通大学电气工程学院（Chengdu：College of Electrical Engineering，Southwest Jiaotong University），2010.