含串补电容的超高压输电线路暂态保护判据

刘 宇，邰能灵，范春菊，于仲安，孟 晓

（1.上海交通大学电气工程系，上海200240；2.江西理工大学电气工程与自动化学院，赣州341000）

超高压线路中增设串补电容能提高超高压线路的有效输电功率，减少输电线线损，增加系统暂态稳定性，改进系统电压水平[1]。但串补电容的接入改变了线路阻抗特性，导致线路测量阻抗在串补电容处突变，使原先的保护失去选择性与方向性。

暂态信息能有效区分区内外故障。文献[2]提出故障瞬间的高低频带能量比法，取得了良好效果；文献[3]中结合高低频能量比、模极大值比率及模极大值时刻判断区内外故障。本文运用对称的三相电流模变换，采用高频与次高频能量积分比提出一种新的暂态保护判据，并通过仿真验证其有效性。

1 暂态保护与小波变换

暂态保护检测由故障暂态产生的高频信号。故障发生瞬间，在两母线间会产生行波的反射与折射，导致暂态信号中出现不同频率的分量[4]。

由于故障暂态时间很短，相比于分析周期信号的傅里叶变换，小波变换更适合分析暂态信号的特征。若信号最高频率为fs，则其被分解为细节系数Di对应的高频带[fs/4，fs/2]，[fs/8，fs/4]，…，[fs/2n+1，fs/2n]以及低频系数Ai对应低频带[0，fs/2n+1]。n=3时的正交小波变换过程如图1 所示。

2 含串补电容的暂态特性分析

2.1 故障电流波过程

高频时，传输线的电阻与电导远小于电抗与电纳，可忽略不计。同时，传输线对地分布电容C与频率无关，高频信号的传输线分布电感L 趋于常数，因此波速为纯阻性常数[5]。

系统故障时产生的高频宽带暂态电流从故障位置开始沿输电线路传输，一部分在母线处反射，另一部分透射至下一条输电线。系统等效为双端电源系统，如图2 所示，P 端为供电端，N 端为受电端，电源内阻分别为ZP与ZN。三条母线P、M、N 间分别存在长距离架空输电线路。以串补电容装设于M 母线出口处为例，讨论不同故障位置F1（PM架空线路内）、F2（串补电容C 左侧保护装置右侧）、F3（MN 架空线路内）情况下的故障特点。

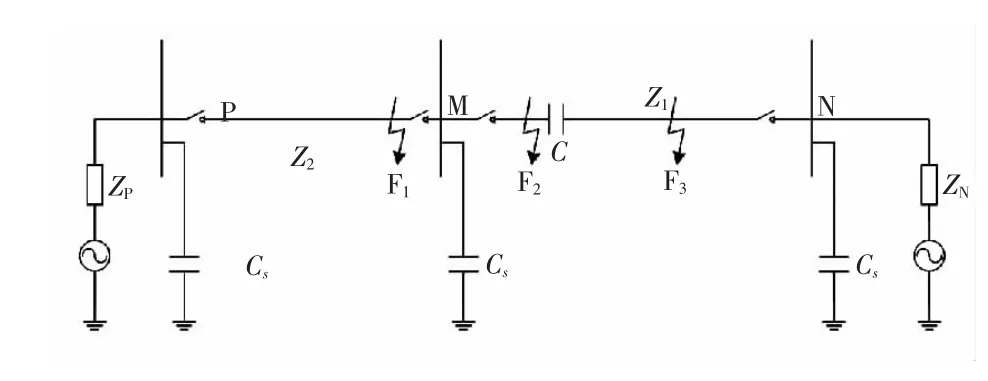
图2 系统波过程等效电路Fig.2 Equivalence circuit of system wave process

假设输电线路PM、MN 波阻抗分别为Z1、Z2，串补电容为C，母线对地分布电容为Cs。故障电流波分别在母线对地分布电容和串补电容处发生透射和反射。

在母线对地分布电容处，母线M 左侧波阻抗为Z2，右侧波阻抗为Z1//（1/jωCs），故电流波透射系数为

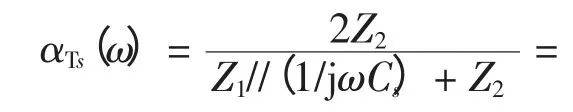
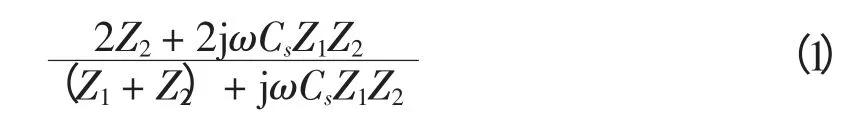
反射系数为

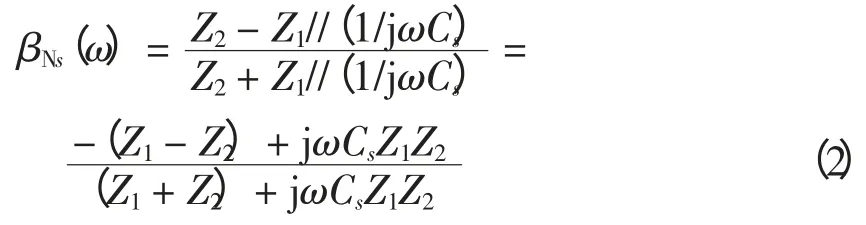
在串补电容处，其左侧波阻抗为Z1，右侧波阻抗为Z1+1/jωC，故电流波透射系数为

反射系数为

2.2 不同故障点位置的电流特性分析

以线路MN 内N 侧出口保护为例。此时，F1为外部故障，F2、F3为内部故障。假设图2 中故障点向右传播的电流为保护安装处向右传播电流为I+。运用彼得逊法则分析暂态电流由故障点至保护安装处的变化，忽略电流通过线路的衰减。

F1处故障时，电流波经母线对地分布电容以及串补电容作用后，保护安装处电流波与线路故障点电流波比值为

由于架空线PM 与MN 波阻抗Z1与Z2近似相等，为简化计算假设Z1=Z2，则式（5）简化为

由式（6）可知，F1处故障的电流波等效于经过传递函数为H1L的低通滤波及传递函数为H1H的高通滤波，截止频率分别为ω1L和ω1H，其中：

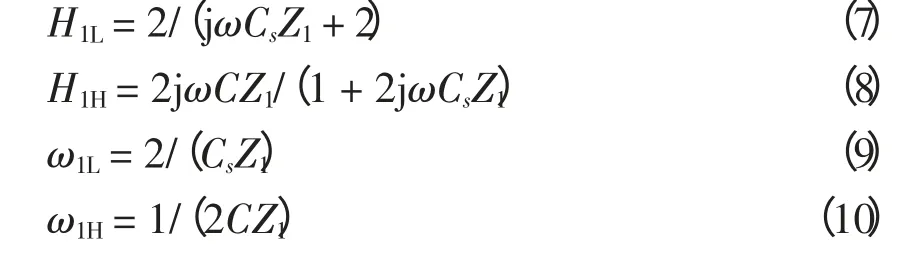
F2处故障时，电流波形经串补电容作用，保护安装处电流波与故障点电流波比值为

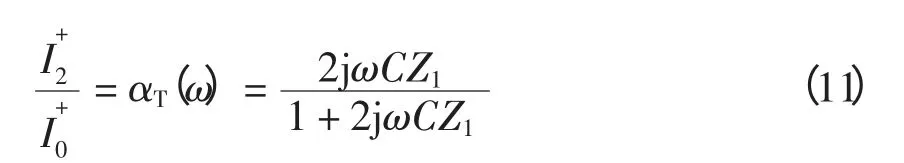
由式（11）可知，F2处故障的电流波等效于经过传递函数为H2H的高通滤波，截止频率为ω2H，其中：

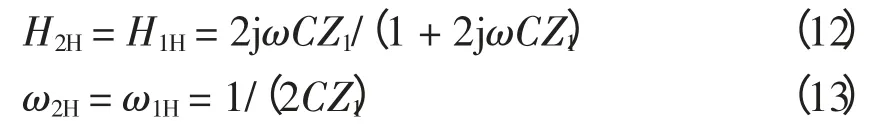
由于母线对地分布电容约0.1 μF[6]，而典型的输电线路串补电容一般取输电线电抗的40%[7]对应的电容值，远大于0.1 μF，即Cs≪C，故：

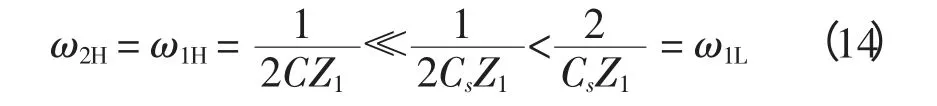
F3处故障时，由于忽略线路损耗，保护安装处电流波与故障点电流波比值为

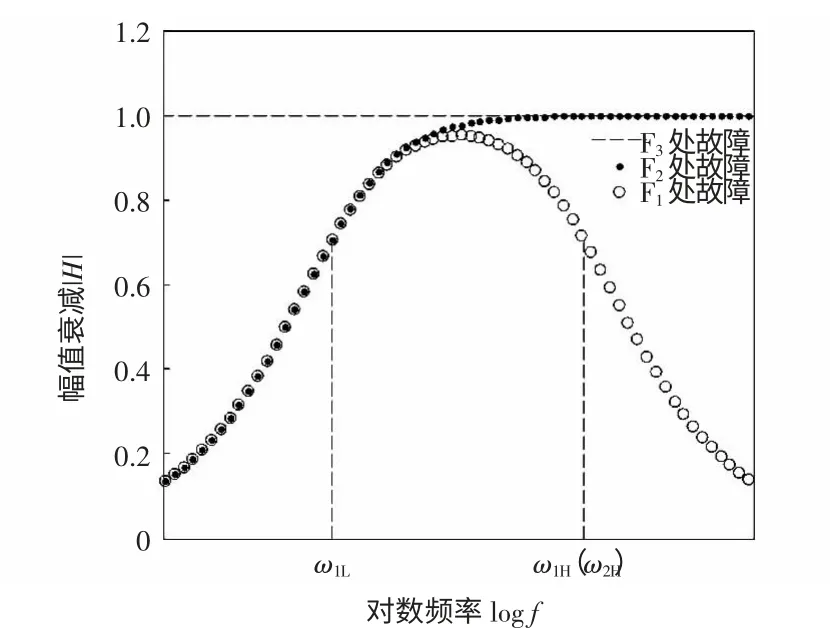
图3 保护安装处与线路故障点处电流比幅频特性Fig.3 Magnitude-frequency characteristics of the current ratio between protection installation position and transmission line fault position

3 高频/次高频能量积分比方法

定义ED1、ED2分别为高频、次高频分量能量，分别表示小波变换中n1、n2层细节系数Dn1与Dn2重构电流D1与D2的能量，其中Dn1对应的高频频段高于Dn2（n1＜n2）；ID1、ID2分别为高频和次高频分量能量的积分，积分时间窗长度为t积分。则有

由故障电流波过程以及电流特性分析可知，区内故障F2、F3处的高频次高频带能量比值高于区外故障F1处的高频次高频带能量比值，因此使用高频分量能量与次高频分量能量比值ED1/ED2能区分出区内外故障。

为了躲开系统干扰产生的高频带分量对于保护装置的影响，减少保护对高频噪声的敏感性，采用连续n（≥5）次满足条件保护才动作的方式。由于高频次高频带能量比ED1/ED2波动较大，采用高频次高频带能量积分比ID1/ID2能有效平滑波动，使保护具有更高的可靠性。

以图2 中线路MN 母线M 侧出口处的C 相单相接地故障为例。保护安装处为线路MN 上N 侧出口。能量比ED1/ED2与能量积分比ID1/ID2的判据结果分别如图4、图5 所示。

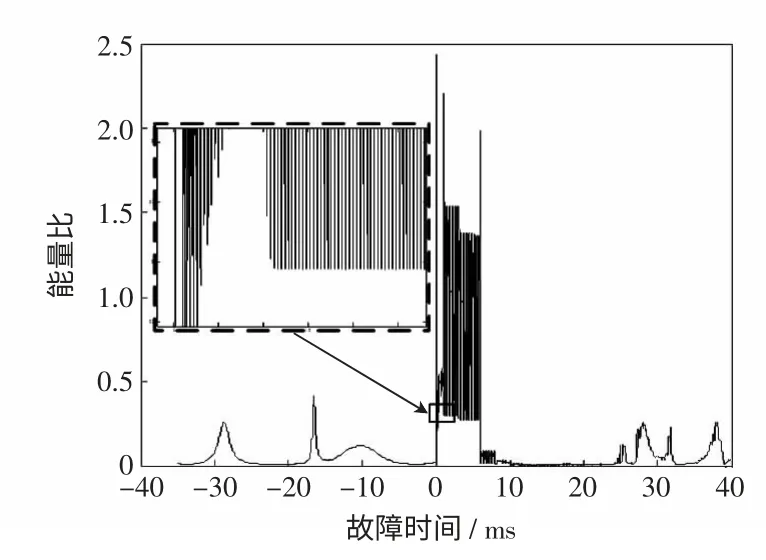
图4 能量比随时间变化Fig.4 Change of energy ratio over time

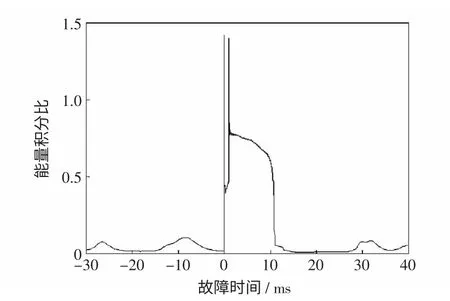
图5 能量积分比随时间变化Fig.5 Change of energy integration ratio over time

由图4 可见，可以采用能量比故障后高于故障前的特征构成保护判据。考虑保护可靠性，判据限值需躲开正常运行时的波动尖峰（例如图4 中故障时刻前17 ms）可能导致的误动，同时需躲开故障后的10 ms 内能量比的巨大波动可能产生的拒动。

由图5 可见，运用能量积分比作为保护判据时，非故障时比值更低更平滑，同时故障后一段时间内（大于10 ms）比值稳定保持在较高水平，有利于保护限值的选取和保护的正确动作。

4 保护判据

保护判据为：能量积分比k 超过对应故障类型的整定值k0。为保证可靠性，要求连续超过5 次整定值（1 ms 计算1 次k 值）。针对不同故障类型给出不同的整定值，以提高保护灵敏度。

以图2 中线路MN 中母线N 侧保护为例。定义能量计算时间窗为t能量，积分时间窗为t积分，采样频率为fs。则采样时间窗为（t能量+t积分），窗内采样点数为（t能量+t积分）fs。为保证各类故障的对称性，取模量电流Im为各相电流Ia、Ib、Ic的均方根，并对采样序列二范数归一化，即

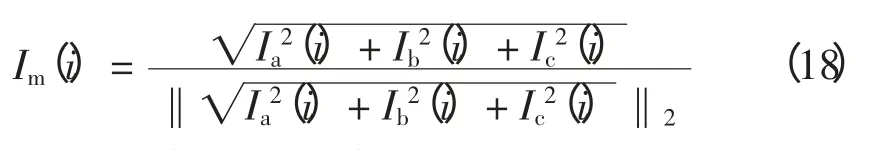
其中，i=1～[（t能量+t积分）fs]。

为保证各类故障的对称性，小波变换选用具有正交、紧支以及高阶消失矩的db5 族小波[8]。采样时间间隔为1/fs。运用细节系数Dn1与Dn2（n1＜n2）重构高频带、次高频带电流值D1与D2，并计算对应能量ED1、ED2，即

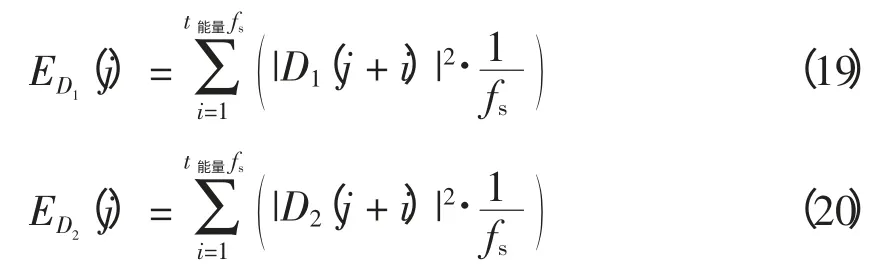
其中，j=1～（t积分·fs）。

则能量积分ID1、ID2分别为

能量积分比为

综上所述，能量积分比计算公式为

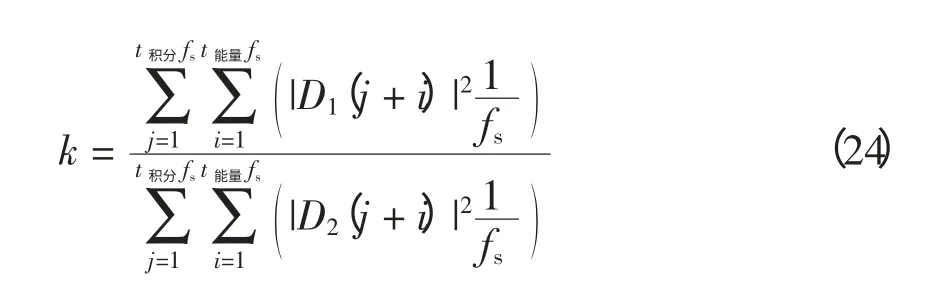
保护流程如图6 所示。

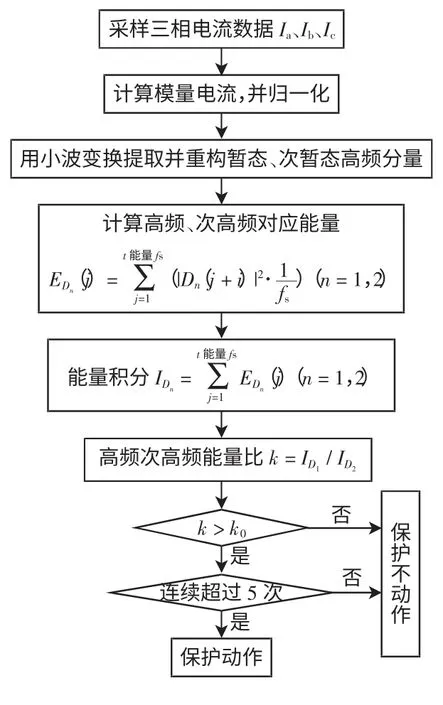
图6 保护流程Fig.6 Flow chart of protection criterion

5 仿真验证

5.1 系统参数

根据图2 在PSCAD 中构建系统仿真图。系统电压为500 kV，左侧电源功角为20°，右侧电源功角为0°；母线对地分布电容[6]为0.1 μF，相间分布电容取0.05 μF；输电线电抗[6]为0.278 Ω/km。串补电容补偿度[7]为输电线电抗的40%，即98.293 μF；系统外的等效阻抗为3+j30 Ω。具体参数如表1所示。PSCAD 中输电线建模运用frequency dependent（phase）model，具体参数[9]如表2、表3所示。

5.2 仿真结果

PSCAD 仿真得到图2 中故障后线路MN 内N侧保护所测电流。高频频段取第1 层小波变换的细节Dn（1n1=1）频段25～50 kHz，次高频频段取第2 层小波变换的细节Dn（2n2=2）频段12.5～25 kHz，能量计算时间窗为t能量=5 ms，积分时间窗为t积分=5 ms。

对不同故障时间、不同故障类型以及不同故障位置（图2 中线路MN 不同位置、串补电容左侧、线路PM 不同位置等）进行大量验证。图7 为某典型故障前后保护安装处电流的能量积分比计算结果。其保护安装位置为线路MN 内N 侧，故障类型为系统C 相单相接地故障。

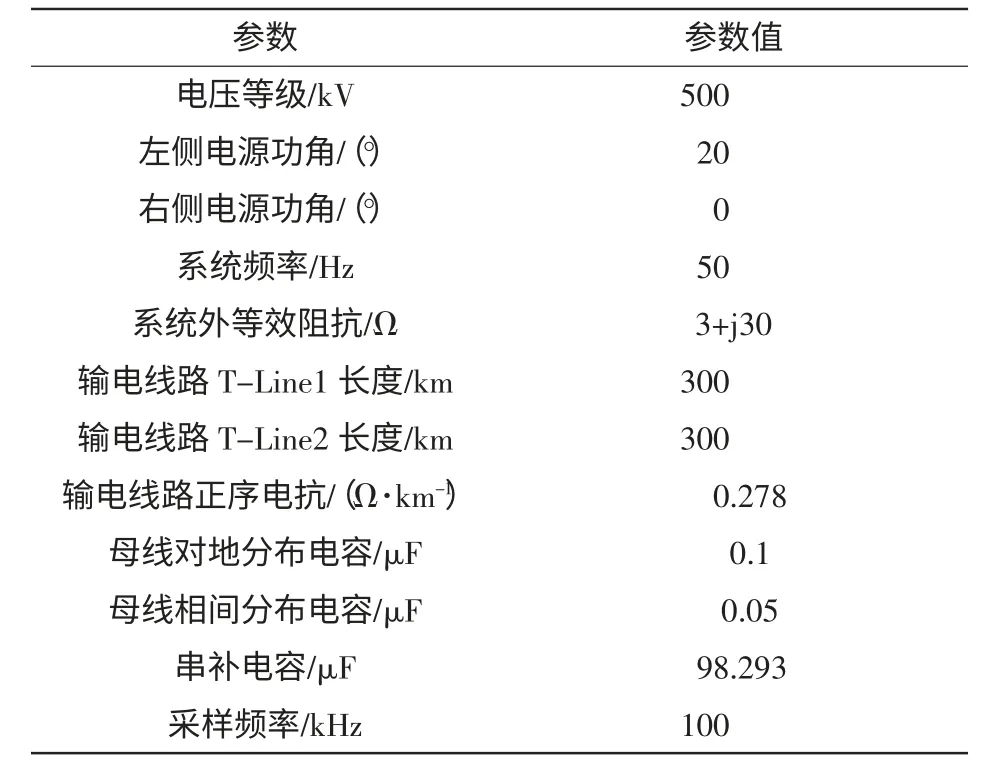
表1 系统参数Tab.1 System parameters

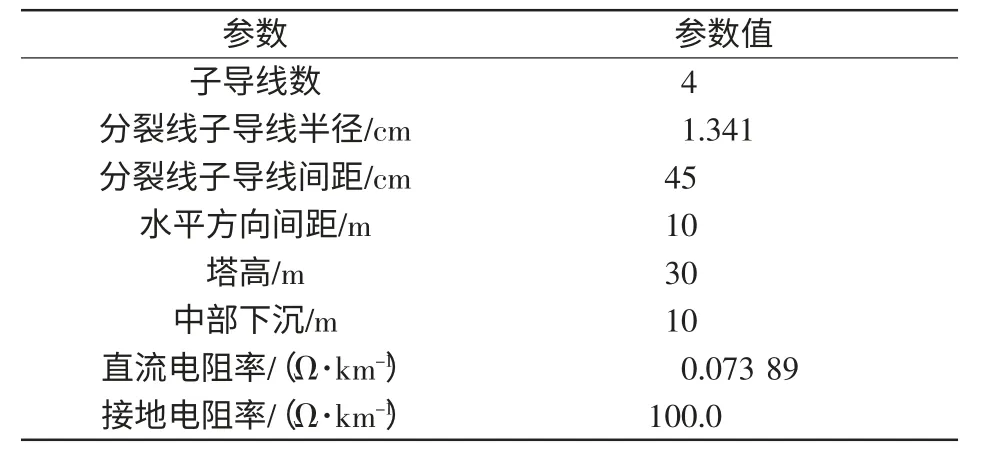
表2 输电导线参数Tab.2 Transmission line parameters

表3 接地导线参数Tab.3 Ground line parameters

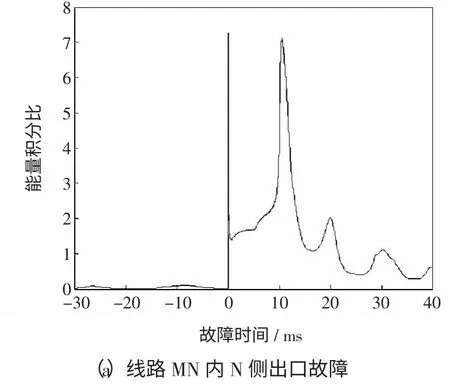
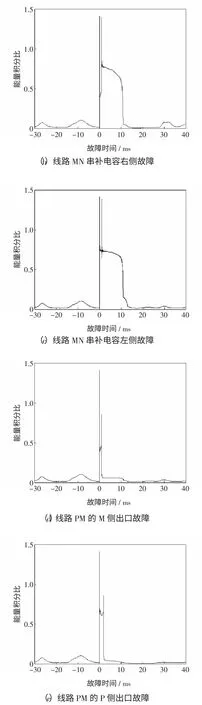
图7 C 相接地故障的能量积分比Fig.7 Energy integration ratio of phase C ground fault

由图7 可见，在故障前，系统能量积分比微幅振荡；在故障发生时刻，对于区内故障，能量积分比陡增，而后经振荡稳定在较高水平，并持续一定时间（10 ms 以上）；对于区外故障，能量积分比陡增后在短时间（2.5 ms 以内）内跌落至较低值。

本判据中，采用先选相，再判断是否越限的方法，有效增加灵敏度。考虑各种故障类型、故障时间以及大量故障位置，最差情况下的故障限值与灵敏度如表4 所示。修改原系统的验证条件，分别验证以下情况：大过渡电阻故障（300 Ω）、轻载（相角差5°）、重载（相角差70°）、大运行方式（电源内阻10+j100 Ω）的保护判据效果。经验证，保护均可正确动作。限于篇幅，仿真结果不再列出。

表4 保护判据测试结果Tab.4 Criterion testing results

6 结论

1）运用能量积分比的方法作为保护判据，与传统的串补电容暂态保护的能量比判据相比，可靠性、灵敏度更高，保护动作更稳定，并能更好地躲开系统中的高频干扰。

2）新方法仅需保护单侧电流量，能有效地在含串补电容的超高压线路上对于不同类型故障正确动作。同时具有较强的抗过渡电阻能力，在不同负荷和不同运行方式下均有较好的动作特性。

3）由于能量积分比判据引入了积分，采样与计算时间窗长度增加，计算时间复杂度和空间复杂度较高。

[1]范秀菊，王增平.一种解决串补电容对距离保护影响的方法[C]//中国高等学校电力系统及其自动化专业第二十五届学术年会，长沙：2009.

[2]刘俊岭，朱江涛，尤卫华（Liu Junling，Zhu Jiangtao，You Weihua）.基于小波包变换的暂态电流保护在带固定串补的超高压线路上的应用研究（Research on application of wavelet packet transform based boundary protection on fixed series compensated EHV transmission lines）[J]. 广东电力（Guangdong Electric Power），2006，19（12）：9-13.

[3]宋丽群，徐波，韩笑（Song Liqun，Xu Bo，Han Xiao）.考虑串补电容的超高压输电线路暂态保护判据研究（Research of protection criterion for EHV transmission line with compensating series capacitor）[J].电力自动化设备（Electric Power Automation Equipment），2005，25（1）：37-39.

[4]王晓东，邰能灵（Wang Xiaodong，Tai Nengling）.基于暂态能量的超高压串补线路故障选相（Fault phase selection for series compensated extra high voltage transmission lines based on transient energy）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（5）：105-109.

[5]格里维.高频传输线的物理基础[M].上海：上海科学技术出版社，1984.

[6]胡巨，杨明玉，陈茂英（Hu Ju，Yang Mingyu，Chen Maoying）.基于小波变换的超高压输电线路故障选相新原理（A new theory for fault phase determination of EHV transmission lines based on wavelet transformation）[J]. 广东电力（Guangdong Electric Power），2005，18（1）：1-4.

[7]何尔文（He Erwen）.串联补偿装置对电网运行安全影响的研究（Resarch of SCC Influence on the Safety of the Power Grid Operation）[D].重庆：重庆大学电气工程学院（Chongqing：College of Electrical Engineering，Chongqing University），2006.

[8]李先允，韩笑，宋立群，等.小波变换在串补超高压输电线路故障分析中的仿真研究[C]//中国高等学校电力系统及其自动化专业第20 届学术年会，郑州：2004.

[9]高立克（Gao Like）.串补电容对广西电网继电保护装置动作特性影响的研究（Research of SCC Influence on the Protective Relays Characteristics of Guangxi Power Grid）[D].南宁：广西大学电气工程学院（Nanning：College of Electrical Engineering，Guangxi University），2009.