岸桥并行作业效率约束下泊位与岸桥集成分派

高超锋，胡志华,2

(1.上海海事大学 物流研究中心，上海201306；2.同济大学 经济与管理学院，上海 200092)

0 引 言

对于集装箱码头，通过靠泊计划和岸桥分派，及其集成分派优化船舶在港作业时间，不仅能够降低运作成本，而且能够提升整个运输网络系统的运作效率[1-4]。泊位与岸桥集成分派(Berth-Crane Allocation Problem，简称BCAP)是指船舶到港之前根据各个泊位的空闲情况和物理约束为船舶安排停靠泊位和靠泊顺序，并配置岸桥。

泊位分派与岸桥调度通常作为两个独立的环节分别进行研究[5-7]。泊位分配与岸桥调度相互影响，将泊位分派与岸桥调度作为整体进行集成调度能够提高港口码头的作业效率。A.Imai，等[8]考虑了岸桥移动路径建立了同时优化离散泊位分配与岸桥调度的模型；Y. M. Park，等[9]建立了带有偏离偏好泊位惩罚的最小费用泊位动态分配模型，并给出每个时间点为船舶作业配备的岸桥数量；M.Sammarra，等[10]建立岸桥作业顺序和岸桥移动路径优化的模型，采用禁忌搜索算法求解；R.M.Tavakkoli，等[11]给岸桥作业完成时间和船舶延迟到港时间赋予相应的权重，建立岸桥分派模型；P.Legato，等[12]考虑船偏好泊位和时间，以船舶作业时间和岸桥使用数量最少为目标建立泊位分派和岸桥分派模型。以上的研究仅从船舶在港等待时间，运作成本、偏好位置，岸桥移动路径等角度考虑泊位—岸桥调度优化问题，很少涉及多台岸桥同时作业的情况下，岸桥边际效率减少的泊位与岸桥调度优化。

Y.M.Park，等[9]的研究表明，为一艘船舶同时服务的岸桥数量约为2～5台。当为一艘船舶同时服务的岸桥数量大于1，则称之为并行作业。分配给船舶的岸桥数量决定船舶挂靠以后的作业效率，船舶的装卸作业时间和分配给它的并行作业的岸桥数量成反比，即岸桥数量越多，作业时间越短。但是，分配给船舶的单个岸桥的作业效率随着并行作业岸桥数量的增多，因相互之间干扰增大而降低。靳志宏，等[13]将岸桥划分为固定岸桥及调度岸桥两子集，并且不同类型的岸桥作业效率不同，设计开发了遗传算法，但没有考虑多台岸桥同时为一艘船舶工作时相互之间存在的干扰对岸桥作业效率的影响。F.Meisel，等[14]从靠泊位置的变化对岸桥作业效率产生影响和岸桥边际效率减少的角度进行研究，但是没有对每个时刻为船舶分配的岸桥数量变化对效率的影响进行分析，因为每个时刻船舶可用岸桥数量增加时，即并行作业的岸桥数量增加，相互之间干扰增大。C.J.Liang，等[15]考虑了岸桥配置数量对岸桥平均作业效率的影响，但是没有考虑偏好泊位和并行作业岸桥相互的干扰。

不同数量的岸桥同时为一艘船舶工作时，对单个岸桥作业效率的影响不尽相同，相同数量的岸桥由于作业人员技术和作业环境的不同对效率的影响也不同，因此引入干扰因子研究船舶在港惩罚成本和岸桥作业时间的变化趋势。另外，为了考虑偏离偏好泊位的影响，通过引入偏离最佳偏好泊位的惩罚系数来研究对船舶在港惩罚成本和岸桥作业时间的影响。最后，考虑多台岸桥并行作业之间的相互干扰，研究并行作业的岸桥台数对泊位与岸桥集成优化的影响。笔者对这些因素进行了综合考虑、建模与分析。

1 问题描述

为了实现泊位与岸桥的集成调度，参照Y.M.Park，等[9]的研究，将泊位分配和岸桥分派问题用图1的“时间-空间”表示。

图1 泊位岸桥集成调度Fig.1 Chart of berth-crane integrated scheduling

“时间-空间”图由网格组成，一个网格表示一个单位时间和一个单位岸线，船舶占用网格表示在该事件和该位置进行装卸作业。在图1中，引入0/1变量Zk,i,j，表示船舶k是否从由靠泊时间j和靠泊位置i表示的位置开始作业。而方框表示该船舶占用的岸线(纵向)与作业的时间(横向)，方框中圆圈中的数据代表每个时刻分配给该船舶的岸桥数量。

集装箱港口根据船舶到港情况分配泊位。通常集装箱都是暂时存放在堆场中，船舶靠泊时希望靠近其特定的堆场位置，这样方便集卡把集装箱从岸边运送到堆场。这个位置相对应的岸线，即是船舶偏好的靠泊位置。如果实际分配的靠泊位置与最佳靠泊位置不一致，如图1，将使集卡水平运输距离增加，导致岸边作业效率下降，船舶需要更多的岸桥工时。为此引入靠泊位置左偏离变量BLk和右偏离变量BRk，将靠泊位置和岸桥工时联系起来，如图2。

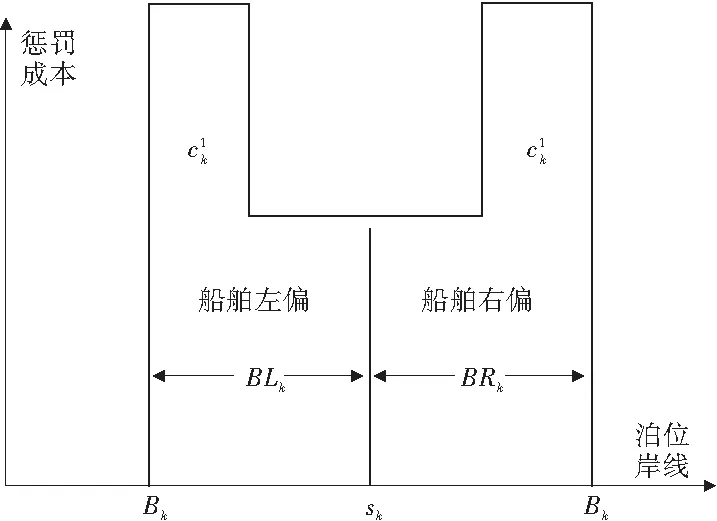
图2 偏离最佳泊位惩罚成本Fig.2 Penalty costs off the optimal berthing position

定义Bk和sk分别表示船舶k的实际靠泊位置和最佳偏好泊位，从船舶左偏离量要求满足约束BLk≥Bk-sk，船舶右偏离量要求满足约束BRk≥sk-Bk。通过ak指定岸桥作业工时，则岸桥作业工时ak会因为作业效率的下降而隐性增加，可以表示为1+β(BLk+BRk)ak。β= 0.01表示若靠泊位置偏离其偏好位置1单位，其岸桥作业工时会隐性增加1%。船舶都有时间窗的约束，ek是船舶预期到达港口的时间，Tk是船舶实际到港时间，船舶提前到达港口的时间TEk=ek-Tk，推迟到达港口的时间TLk=Tk-ek，如图3。

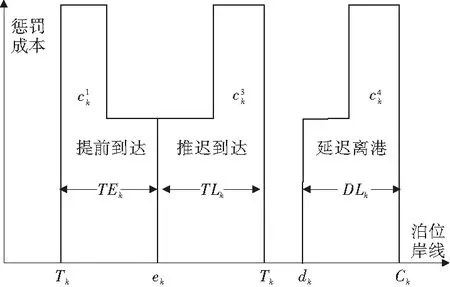
图3 提前、推迟、延迟时间惩罚成本Fig.3 Penalty costs for time advancement and delay

当有多个岸桥同时服务于一艘船的时候，随着岸桥数目的逐渐增多，岸桥的装卸效率因为岸桥并行作业之间的干扰而产生变化。因此，引入岸桥干扰因子α，规定α≤1。ak表示完成船舶k作业需要的岸桥总台时数，Yk,j表示j时刻分配给船舶k岸桥数量，把偏离最佳泊位的影响一起考虑，则需要满足如式(1)的约束条件：

(1)

因为α≤1，所以需要增加岸桥数量或者延长船舶在港操作时间来抵消岸桥边际效率减少的影响。随着每个时刻的岸桥数的增加，则岸桥并行作业之间的干扰是怎样变化，增加多少个岸桥才是合理的。如果延长船舶在港操作时间，则可能会造成船舶延迟离港，船舶延迟离港惩罚成本增加。

2 模 型

在模型中引入多台岸桥同时工作的干扰因子α和泊位偏移系数β。如果多台岸桥同时工作，相互之间存在一定的干扰，从而会降低岸桥工作效率。当船舶没有停靠在偏好泊位时，同样会对岸桥工作效率产生影响。为使模型设计与分析之便，将干扰系数与偏离惩罚系数设置为决策变量，即根据不同的岸桥数量产生不同的干扰率，根据偏离偏好泊位惩罚系数的大小产生不同的效率影响。并且，为重点研究干扰问题，考虑以下作业特征的泊位与岸桥集成分派问题：待靠泊的船舶没有吃水和水深等约束；每条船都必须且只能靠泊一次，不考虑船舶靠泊后的移泊情况；船舶装卸作业不能在中途停止；每艘船舶接受服务的岸桥数目有上下限制；若提供某个船舶服务的岸桥超过2个以上，则岸桥的工作效率受到影响。

2.1 集合、参数与决策变量

2.1.1 集 合

sl= {1，2，…，sls}，表示船舶序号集合，k，k-和k+表示其中的船舶；

sm={1，2，…，sms}，表示岸线分段集合，i，i-和i+表示其中的分段位置；

sn={1,2，…，sns}，表示时间分段集合，j，j-和j+表示其中的时段。

2.1.2 参 数

ek指定预期到达时间；

ak是以单位桥时计算的总的岸桥作业时间；

bk是船长；

dk是船舶离开的最晚期限；

sk是船舶的偏好泊位；

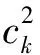
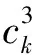
lk指定可以分配给船的最少岸桥数量；

uk表示能分配给船舶的最大岸桥数量；

c是港口可用岸桥的总数量。

2.1.3 决策变量

Xk,i,j是0/1变量，表示船舶k是否停靠在时空网格(i，j)作业，是为1，反之为0；

Zk,i,j是0/1变量，表示如果船舶k在时空网格(i，j)开始作业，是为1，反之为0；

vk,j表示船k是否在j时刻作业，是则为1，反之为0；

Uk,j表示船舶k是否占用位置i，是则为1，反之为0；

Yk,j表示在j时刻分配给船k的岸桥数量；

Ck表示船舶装卸作业的完成时间；

BLk表示船舶在岸线维度的左偏离长度；

BRk表示船舶在岸线维度的右偏离长度；

TEk表示靠泊的提前时间长度；

TLk表示靠泊的推迟时间长度；

DLk表示相对于最晚离泊要求的延迟时间长度；

2.2 考虑岸桥并行作业效率约束BCAP模型

在Y.M.Park，等[9]的模型的基础上，引入并行作业岸桥干扰因子和偏离偏好泊位的惩罚系数，构建船舶在港惩罚成本最小的泊位与岸桥的集成分派模型。

2.2.1 目标函数

最小化船在港总惩罚成本：

minf=(f1,f2,f3,f4)

(2)

2.2.2 约束函数

每艘船的操作时间要求必须满足：

(3)

每一个时间段可供分配的岸桥数目不超过岸桥总数量：

(4)

式(5)和式(6)定义Y和v之间的关系：

vk,j≤Yk,j,∀k,j

(5)

Yk,j≤M·vk,j,∀k,j

(6)

分配的岸桥数量，满足可为该船舶服务的岸桥数量的上下限约束：

Yk,j+M·(1-vk,j)≥lk,∀k,j

(7)

Yk,j≤uk,∀k,j

(8)

离左边最佳停泊位置的距离：

BLk≥Bk-sk,∀k

(9)

离右边最佳停泊位置的距离：

BRk≥sk-Bk,∀k

(10)

提前到达时长：

TEk≥ek-Tk,∀k

(11)

推迟到达时长：

TLk≥Tk-ek,∀k

(12)

延迟离港时长：

DLk≥Ck-dk,∀k

(13)

船舶离港时间必须在岸桥作业结束时间之后，即：

Ck≥vk,j·(j+1),∀k,j

(14)

式(15)定义一个时空网格最多被一条船占用：

(15)

式(16)和式(17)约束v和X之间的关系：

(16)

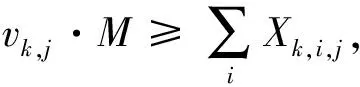
(17)

式(18)和式(19)约束U和X之间的关系：

(18)

(19)

式(20)保证船靠泊空间上的连续性：

(20)

式(21)保证船接受岸桥作业时间上的连续性：

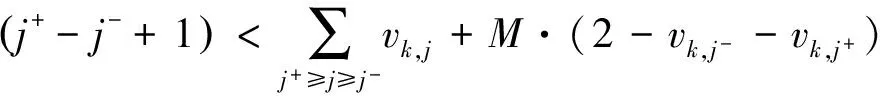
(21)

式(22)约束v和Z在时间上的关系：

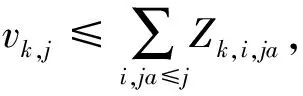
(22)

每艘船只能靠泊一次：

(23)

船靠泊在计划的时空矩形内，Xi,j,k才能取值1：

∀k,(sms-bk)≥i-≥2

(24)

定义船停靠位置的临界条件：

(25)

(26)

保证在时空网格图中船舶靠泊矩阵的宽度等于船的长度：

(27)

2.3 BCAP模型转换

在2.2的模型中，式(3)是非线性的约束条件，下面把该约束条件转换为线性约束。

在Meisel模型[14]的基础上,将偏离最佳泊位分为左偏离和右偏离，这样避免了Meisel模型计算泊位偏离的误差，同时把偏离最佳泊位的惩罚成本作为目标函数，并且在算例中设定可用岸桥数量是变化的集合，用于分析在不同程度的干扰环境下岸桥数量变化对效率的影响。

在下面的模型中，引入以下变量：vk,j,q表示q个岸桥在j时刻分配给船舶k,则为1，否之为0；yk-,k+表示船舶k-在船舶k+之前靠泊，则为1，否之为0；zk-,k+表示船舶k-在船舶k+之前由岸桥开始对之作业，则为1，否之为0；定义岸桥数量集合R≡{q:lk≤q≤uk}，通过q进行索引。

2.3.1 目标函数

最小化船在港总惩罚成本：

minf=f1+f2+f3+f4

(28)

2.3.2 约束函数

多台岸桥并行作业互相干扰及泊位偏移的影响下，须满足每艘船的操作时间要求：

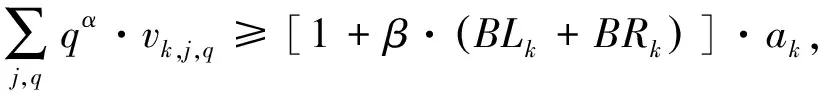
(29)

满足最大岸桥数量限制：

(30)

每艘船舶作业开始与结束时间的关系如式(31)～式(33)：

(31)

(32)

j·vk,j+sns·(1-vk,j)≥Tk,∀k,j

(33)

两艘船舶停靠的位置关系：

Bk++M·(1-yk-,k+)≥Bk-+bk-,∀k-≠k+

(34)

两艘船舶停靠时间的关系：

Tk++M·(1-zk-,k+)≥Ck-,∀k-≠k+

(35)

避免两艘船舶之间在停靠时间和停靠位置上的冲突：

yk-,k++yk+,k-+zk-,k++zk+,k-≥1,∀k-≠k+

(36)

船离港时间必须小于最大时间窗：

Ck≤sns,∀k

(37)

保证每艘船均停靠在岸线范围内：

0≤Bk≤sls-bk,∀k

(38)

3 算例与分析

以上海市洋山港集装箱码头为例，验证泊位与岸桥集成分派方法。泊位岸线长1 200 m，以50 m作为一个泊位单位，仿真服务周期48 h，1 h为一个时间单位。岸桥总数为16台。同时为一艘船舶服务的岸桥数量有上下限约束，最小量是船公司和集装箱码头签署的合同决定，最大量是由可用岸桥数量决定。

为了模拟多船型的泊位与岸桥集成调度，列出了4种船型的相关参数。船舶到达时间ek随机取自区间[1，35]，船舶偏好位置sk随机取自区间[1，20]，船舶离开时间dk随机取值([4，8] +ek)，船舶作业时间ak随机取自区间[10，45]，不同类型的船舶参数取值范围不同，如表1。

表1 种类型船舶的参数

3.1 靠泊位置对船舶在港惩罚成本和岸桥作业时间的影响

偏离最佳泊位的惩罚系数即偏离系数β在0～0.04之间依次递增，岸桥可用数量集的范围取[3，5]，即岸桥最大可用数量为5个，最小可用数量为3个，运行结果得到表2，岸桥总工时指每个时刻工作的岸桥数量总和，简称桥时。

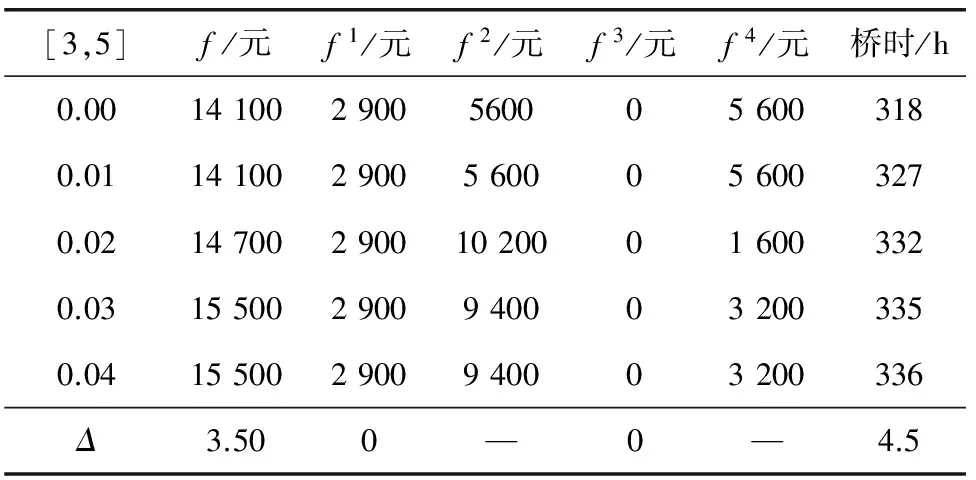
表2 偏离最佳泊位的惩罚系数影响的计算结果

注：Δ=[(f2-f1)+(f3-f2)+(f4-f3)+(f5-f4)]/4。

由表2可知，随着偏离最佳泊位惩罚系数增大，船舶在港惩罚成本平均增长率为12.07%，岸桥总工时平均增长率为1.39%。因为偏离最佳泊位的惩罚系数β增大，则1+β(BLk+BRk)ak增大，根据约束条件(3)就需要更多岸桥工时才能满足，增加了船在港操作时间，相应的船在港惩罚成本增加；偏离最佳泊位同时会引起集卡交叉作业或者加长路线，则港口的运营成本增加。

偏离最佳泊位的惩罚成本没有变化是因为惩罚系数一定的情况没有改变整个集成调度系统的泊位分配，当不同船舶的惩罚系数不同时，则偏离最佳泊位的惩罚成本就会改变。

当β=0～0.02，随着偏离最佳泊位惩罚系数增大，船舶提前到港的惩罚成本增加，而延迟离港成本减少。原因是随着偏离最佳泊位惩罚系数增大，船舶在港操作时间增加，为了规避高额的延迟离港惩罚成本的增加，船舶会选择提前到达港口。

当β=0.02～0.04，随着偏离最佳泊位惩罚系数增大，船舶提前到港的惩罚成本减少，而延迟离港成本增加。这是因为船舶都有时间窗约束，不可能为规避高额的延迟离港惩罚成本，而使整个集成调度系统惩罚成本增加。

3.2 不同的作业环境对船舶在港惩罚成本和岸桥作业时间的影响

由于作业人员技术水平和作业环境的不同对效率产生的影响也不同。作业环境对并行岸桥作业效率的影响通过干扰因子来体现。在干扰因子α在1～0.8之间依次递减，岸桥可用数量的范围取[4，6]时，求解得到如表3的结果。

表3 干扰因子影响的计算结果

从表3可知，随着岸桥并行作业干扰影响的增大(干扰系数的降低)，船舶在港的总惩罚成本f、偏离最佳泊位的惩罚成本、提前到港惩罚成本、推迟到港惩罚成本、延迟离港惩罚成本和岸桥总工时都是增大的趋势。船舶在港的总惩罚成本f平均增加2 750元，岸桥总工时平均增加23.25 h。原因是随着干扰增大，岸桥作业效率递减，船舶所需岸桥工时增加，从而延长操作时间，需要安排船提前到港或者延迟船舶离港，增加船舶在港的惩罚成本。

船舶提前到港惩罚成本、延迟离港惩罚成本都与岸桥干扰影响正相关，而船舶延迟到港惩罚成本一直为0。原因是船舶到港时间比较集中，然而每艘船所需操作时间较大就会要求船提前到达港口，从而增加提前到港惩罚成本，避免高额的延迟离港惩罚成本。

船舶偏离最佳泊位的惩罚成本增加的原因是前一艘船舶在港操作时间延长，当船舶到达港口时，该船舶的最佳泊位被占用，所以船舶只能选择偏离其最佳泊位的位置靠泊，从而增加船偏离最佳泊位的惩罚成本。

3.3 并行作业岸桥数量变化对船舶在港惩罚成本和岸桥作业时间的影响

设置偏离最佳泊位的惩罚系数为β= 0.01，干扰因子α在1～0.8之间依次递减，岸桥可用数量的范围在“[2，4]、[3，5]、[4，6]”依次变化，求解模型得到如表4的结果。

表4 并行作业岸桥数量变化的影响结果

注：Δf=((f|3-5|-f|2-4|)+(f|4-6|-f|3-5|))/2。

通过对表4进行分析发现，随着每艘船舶可用岸桥数量的增加，船舶在港的惩罚成本f呈减少趋势。Δf为负，表示船舶在港惩罚成本与可用岸桥数量呈负相关关系。并且发现，岸桥总工时与可用岸桥数量存在正相关关系，即随着每艘船舶可用岸桥数量的增加，岸桥总工时增加。如图4，岸桥可用数量为[4，6]是最下面的曲线，岸桥可用数量为[2，4]为最上面的曲线。

图4 岸桥数量对船泊在港惩罚成本的影响Fig.4 Effect of cranes numbers on the penalty costs of vessel in port

当每艘船可用岸桥数量从[2，4]增加为[3，5]时，惩罚成本f平均减少43.83%，当岸桥可用数量从[3，5]增加为[4，6]时，惩罚成本f平均减少38.8%；因为船靠泊后并行作业的岸桥数量增加时，加快了货物装卸，则船舶需要的装卸时间减少，相应的会减少船舶延迟离开港口时间，则延迟离港惩罚成本减少；或者因为操作时间减少，可以选择船准时靠泊，则相应提前到港的惩罚成本减少。

如图5，岸桥可用数量为[4，6]的曲线位于上方，岸桥可用数量为[2，4]的曲线位于下方，结果与图4相反。

图5 船舶在港岸桥总工时Fig.5 Cranes total operation time in port

当每艘船可用岸桥数量从[2，4]增加为[3，5]时，岸桥总工时平均增加4.65%，当岸桥可用数量从[3，5]增加为[4，6]时，岸桥总工时平均增加1.58%；因为同时为船舶并行作业的岸桥数量增加，岸桥相互之间的干扰更大，岸桥的装卸作业效率降低，则船需要的总岸桥工时增加。

岸桥数量直接影响岸桥之间的干扰效率，岸桥并行作业的数量越多，则相互之间的干扰越大。虽然岸桥并行作业的数量较多时能够加快船舶的装卸，减少船在港操作时间，满足船在计划的时间内到港和离港的要求，减少船在港惩罚成本，但是却增加了岸桥总工时，导致岸桥工作效率降低，增加港口能源消耗，使得集装箱港口运作总成本增加。港口如何安排合理数量的岸桥为船舶作业，即要能够满足船靠泊时间窗约束，又要能够避免分配的岸桥数量过多，导致并行作业之间的干扰增大，本文为决策者和船舶运营商在处理该问题时提供了解决矛盾的模型和依据。

4 结 语

在连续泊位与岸桥的集成调度模型的基础上，研究岸桥并行作业时相互之间存在的干扰影响岸桥作业效率的问题。分配给同一条船舶的并行作业岸桥之间的干扰会影响岸桥作业效率；当船舶的偏离最佳靠泊位置时，同样数量的岸桥并行作业产生的干扰大小是不同的。

笔者引入岸桥干扰因子和偏离最佳泊位惩罚系数来研究岸桥效率问题，建立了以船总在港惩罚成本最小的混合整数规划模型。仿真分析发现，当岸桥可用数量确定时，随着偏离最佳泊位惩罚系数增大，船舶在港惩罚成本平均增长为12.07%，岸桥总工时平均增长1.39%；随着岸桥干扰因子变小船舶在港惩罚成本平均增长40.08%，岸桥总工时平均增长7.3%。分配给船舶的岸桥可用数量集增大时，船舶在港惩罚成本减小41.31%，但岸桥总工时增加3.12%，这两者的矛盾逻辑上服从二律背反规律，服务与成本的矛盾，船公司希望少付费用而满足自己所有的服务要求，而港口则希望在高质量服务时能够得到高的效益回报。因此，集装箱港口在集成调度中既要充分考虑并行作业的岸桥对服务质量的影响，同时还要充分考虑对作业效率的影响。下一步将在以下两个方面继续进行研究：建立岸桥干扰因子与岸桥分配数量的关系函数，利用启发式算法进行求解大规模问题；根据岸桥作业的实时数据，研究在不确定性作业环境下岸桥并行作业对效率的影响。

[1] Monoaca M F, Sammarra M.The berth allocation problem: a strong formulation solved by a lagrangean approach [J].Transportation Science, 2007, 41(2): 265-280.

[2] Daganzo C F.The cranes scheduling problem transportation research [J].Transportation Research Part B: Methodological, 1989, 23(3): 159-175.

[3] 计明军,靳志宏.集装箱码头集卡与岸桥协调调度优化[J].复旦大学学报:自然科学版,2007,46(4):476-480.

Ji Mingjun, Jin Zhihong.A united optimization of crane scheduling and yard trailer routing in a container terminal [J].Journal of Fudan University:Natural Science, 2007, 46(4): 476-480.

[4] 周鹏飞,康海贵.面向随机环境的集装箱码头泊位-岸桥分配方法[J].系统工程理论与实践,2008,31(1):161-169.

Zhou Pengfei,Kang Haigui.Study on berth and quay-crane allocation under stochastic environments in container termina [J].Systems Engineering Theory & Practice, 2008, 31(1): 161-169.

[5] Li C L,Cai X Q,Lee C Y.Scheduling with multiple jobs on one processor pattern [J].IIE Transaction,1998, 30(5): 433-445.

[6] Imai A,Nishimura E,Papadimitriou S.The dynamic berth allocation problem for a container port [J].Transportation Research Part B: Methodological, 2001, 35(4): 401-417.

[7] Gerald G B,Siriphong L,Katie P T.Optimizing ship berthing [J].Naval Research Logistics,1994, 41(1):1-15.

[8] Imai A,Chen H C,Nishimura E,et al.The simultaneous berth and quay crane allocation problem [J].Transportation Research Part E:Logistics and Transportation Review, 2008, 44(5): 900-920.

[9] Park Y M,Kim K H.A scheduling method for berth and quay cranes [J].Container Terminals and Automated Transport Systems,2003,25(1): 1-23.

[10] Sammarra M,Cordeau J F,Laporte G,et al.A tabu search heuristic for the quay crane scheduling problem [J].Journal of Scheduling,2007, 10 (4/5): 327-336.

[11] Tavakkoli-Moghaddam R,Makui A,Salahi S,et al.An efficient algorithm for solving a new mathematical model for a quay crane scheduling problem in container ports [J].Computers & Industrial Engineering,2009,56 (1): 241-248.

[12] Legato P,Gulli D,Trunfio R.The quay crane deployment problem at a maritime container terminal [C]//Proceedings of the 22ndEuropean Conference on Modeling and Simulation.Campora San Giovanni, Amantea (CS),Italy: [s. n.], 2008: 53-59.

[13] 靳志宏,徐奇,韩骏,等.集装箱码头泊位与岸桥联合动态调度[J].中国科技论文在线,2011,11(6): 809-814.

Jin Zhihong,Xu Qi,Han Jun,et al.United dynamic scheduling of berths and quay cranes in a container terminal with consideration of actual constraints [J].Science Paper Online,2011,11(6):809-814.

[14] Meisel F,Bierwirth C.Heuristics for the integration of crane productivity in the berth allocation problem [J].Transportation Research Part E:Logistics and Transportation Review,2009,45(1):196-209.

[15] Liang C J,Huang Y F,Yang Y.A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning [J].Computers & Industrial Engineering,2009,56(3): Y1021-1028.