随机风作用下高速列车动力学参数的可靠性优化设计*
于梦阁 张继业 张卫华
(西南交通大学牵引动力国家重点实验室,成都 610031)
引言
随着世界高铁的发展,铁路车辆正向高速化和轻量化发展.列车运行速度的提高对列车运行的安全性、稳定性和舒适性[1],尤其是横风环境下的运行安全性提出了新的要求.由于侧风而导致列车脱轨或倾覆的行车事故在各国屡见不鲜.研究表明,当列车的速度超过200 km/h,横风风速大于30 m/s时极有可能导致列车脱轨或倾覆[2,3].因此,非常有必要开展高速列车的侧风运行安全性研究,以提高高速列车的抗风性能.目前在高速列车风致安全方面所做的工作主要是基于确定性的方法,即车辆的空气动力学参数、系统动力学参数和环境参数都是确定不变的[4~7].采用这种确定性的理想计算模型来描述真实的列车系统是有问题的.首先,自然风是个随机过程,不能采用确定性的方法建模.其次,系统的一些参数,如气动力系数难以通过试验或仿真准确给出,需要考虑其不确定性.传统的确定性分析方法计算得到的列车运行安全域只能给出列车运行安全与危险的分界线,不能对不同风速下列车运行的风险进行有效评估.文献[8,9]建立了阵风环境下车辆运行可靠性的分析方法,给出了不同风速下的失效概率.但理想阵风是对自然风的一种抽象形式,只考虑自然风速的最大幅值和持续时间,无法考虑实际自然风的脉动特性.而自然风具有脉动特性,它对结构的作用是一种随机载荷.以上这些研究工作的开展为改善强侧风环境下高速列车的运行安全性提供了方向.在大风地区铁路沿线,合理修建挡风墙可以显著提高强侧风环境下高速列车的运行安全性[10,11],但修建挡风墙工程浩大,造价高,可寻找其它方法来改善高速列车的抗风性能.优化车辆系统动力学参数可以改善高速列车的运行安全性.目前在在列车动力学悬挂参数优化方面所做的工作主要是根据经验设定单个动力学参数的变化范围来研究各个动力学参数对列车的安全性、平稳性及舒适性等方面的影响[12~14].从本质上讲,这些研究工作均为单因素的参数研究或者优选研究,过多地依赖于工程经验,且单因素的参数研究或固定其它参数的多因素优化,得到的优化结果实际上并不是最优,即局部最优化相加不等于全局优化[15,16].为克服这些缺点获得最优的动力学参数,必须采用直接优化的方法.直接优化设计是在满足一定约束条件的前提下,采用数学方法对某些设计目标寻求尽可能最大或最小(轮重减载率最小、临界速度最大等).对于随机风环境下车辆系统动力学参数的多目标优化问题,目前并无相关工作发表,急需开展此方面的研究工作.
本文结合列车空气动力学、车辆系统动力学、可靠性理论及多目标优化理论,建立了随机风环境下高速列车运行安全可靠性的多目标优化模型.以动力学参数为优化变量,以失效概率和轮轴横向力为优化目标,采用多目标遗传算法对动力学参数进行自动寻优,以提高高速列车的侧风运行安全性.
1 多目标优化流程
强横风下高速列车动力学参数的多目标优化设计研究主要涉及如下方面:高速列车空气动力学数值仿真计算、高速列车车辆系统动力学数值仿真计算、可靠性计算、多目标寻优算法、系统集成框架等.在高速列车空气动力学数值仿真计算方面,可以采用商业CFD软件或者自编程序;在高速列车车辆系统动力学数值仿真计算方面,可以采用商业MBS软件或自编程序;在可靠性计算方面,可以采用一次二阶矩方法、Monte Carlo模拟等方法;在多目标寻优算法方面,可以采用遗传算法、神经网络等优化策略;在系统集成方面可以采用商业集成框架或自编的批处理程序.本文随机风作用下高速列车动力学参数的可靠性优化设计流程如图1所示.

图1 动力学参数多目标优化设计流程Fig.1 Multi-objective optimization design process of the kinetic parameters
2 随机风下高速列车非定常气动载荷的计算
2.1 随机风的模拟
风速观测记录表明自然界的瞬时风速包含两种成分:周期在10min以上的平均风和周期在几秒的脉动风.任一点处的风速值w可以表示为:

脉动风的特性可以采用功率谱密度描述,COOPER基于VON KARMAN谱推导了横风下随车移动点的脉动风的功率谱密度[17]:
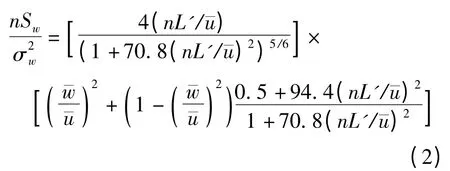
其中,
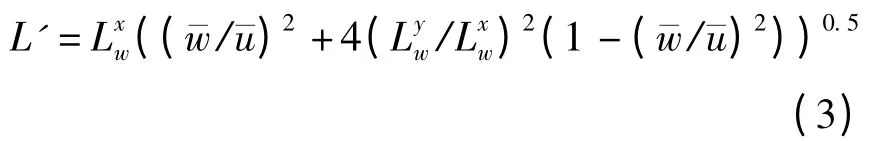
式中:nSw/为脉动风的无量纲功率谱密度;n为频率;Sw为脉动风速的功率谱密度;σw为脉动风速的标准差,σw=;Iz为湍流强度为纵向湍流积分尺度为横向湍流积分尺度;¯u为平均合成风速为车速.
通过数值计算可得到不同离散频率nj下的功率谱密度,进而通过谐波叠加法可得到脉动风速w'的计算公式如下:
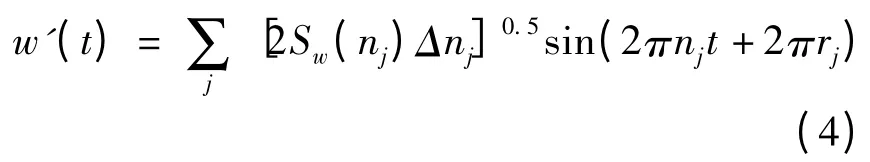
式中:t为时间;Δnj为频率步长;rj为0~1之间的随机数.
2.2 非定常气动载荷的计算
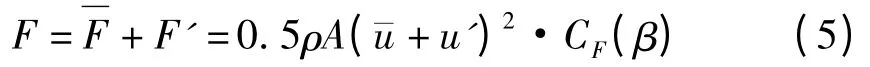
式中,u'为合成风速的脉动值.

Baker[18]对准定常假设进行改进,得到作用于列车上的气动力的脉动值计算公式:

然而,在实际情况下,准定常假设并不是完全成立的.这是由于来流中的小尺度涡流与列车附近流场并不是完全相关的,气动载荷的波动与风速的波动并不是完全一致的.采用空气动力学权重函数可以建立起气动载荷的波动与脉动风速的波动之间的关系,此时气动力的脉动值可通过下式计算[18]:


对于摇头力矩和点头力矩,可认为其波动与风速的波动是一致的.对于气动力矩的计算,只需在气动力计算公式中增加参考高度,并将气动力系数换成气动力矩系数.
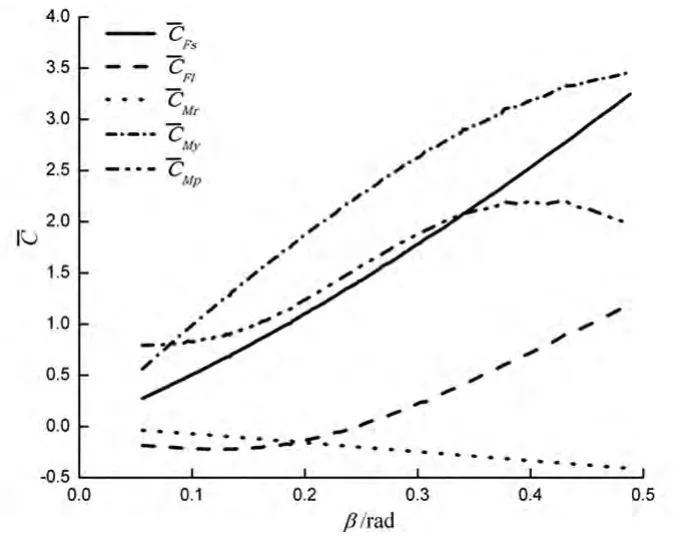
图2 气动载荷系数与侧偏角的关系Fig.2 The aerodynamic coefficients at different wind yaw angles
3 车辆动力学模型
利用SIMPACK软件建立车辆的多体系统动力学模型,如图3所示.单节车的车辆系统动力学模型是由1个车体、2个构架、4个轮对和8个转臂组成.其中刚性车体、构架和轮对均有6个自由度,转臂为1个自由度.整个动力学单车模型共有50个自由度.本文中采用“拖-动-拖”的编组方式,其中拖车和动车在自由度选取、各部件的连接与约束关系、结构及绝大部分悬挂参数等方面完全一致,但在车体质量、重心高度、车体转动惯量等局部参数上有所差异,整车模型共有150个自由度.模型中高速列车的车轮踏面外形采用LMA踏面,钢轨采用T60钢轨,轨道不平顺激励采用国内某高速铁路实测轨道谱.

图3 高速列车多体系统动力学计算模型Fig.3 Multi-body system dynamics computational model of high-speed train
将侧风下作用于高速列车上的气动载荷加载到高速列车多体系统动力学模型中,以分析高速列车的运行安全性.本文将各个部件视作刚体,按照力的平移与等效原则,将作用于车体表面上的分布压力向车体某一点简化,得到作用于车体某一点的集中力和力矩.通过简化可以得到不同风速大小和不同车速下作用于各个车体上的阻力、侧力、升力、倾覆力矩、摇头力矩和点头力矩.
4 可靠性计算方法
4.1 基本随机变量
本文选取随机风速和气动载荷系数为基本随机变量.假设随机风速和气动载荷系数均服从正态分布,从而需要确定出各随机变量的均值和标准差.本文计算的车速为300km/h,平均风速为30m/s.
为了得到较为准确的气动载荷系数的平均值和标准差,需要多个风速样本.经计算发现取200个风速样本可得到较准确的平均值和标准差.通过对200个风速样本下的气动载荷系数的平均值和标准差取平均,可以得到较准确的气动载荷系数的平均值和标准差.表1给出了当车速为300km/h,平均风速为30m/s时,气动力(矩)的标准差.

表1 气动载荷系数标准差Table 1 Standard deviation of the aerodynamic coefficients
4.2 功能函数及失效概率
可靠性分析的关键是对系统的失效概率进行量化,为实现这一目的,称随机函数g≡g(X)为系统的功能函数.规定g(X)>0表示系统处于安全状态,g(X)=0表示系统处于极限状态,g(X)<0表示系统处于失效状态.失效概率可以定义为:

在高速列车横风安全性分析中,轮重减载率是最容易超标的指标[3,6],功能函数与车轮的轮重减载率相关,轮重减载率是随机变量X、车速v和平均风速的函数,即有Q=Q(X;v,).功能函数g(X)与车轮的轮重减载率Q不是完全相同,假设轮重减载率的限值为QL,则功能函数可表示为[9]:
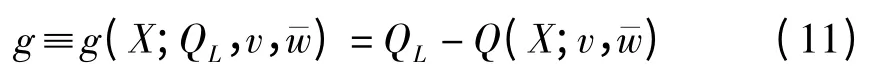
在传统的高速列车横风安全分析方法中,QL的一个广泛使用的值是0.8,对应的安全余量是20%.在本文中,QL取1,对应于传统可靠性分析方法中高速列车安全运行的极限状态.
假设功能函数服从正态分布,其均值为μg,标准差为σg,即有g~N(μg).从而:

将功能函数的均值与标准差的比值定义为可靠指标β,即有

β是一个无量纲数,此时,失效概率可以表示为:

由此可见,失效概率Pf与可靠指标β之间存在一一对应关系.
一次二阶矩方法(FOSM)是可靠性分析中最简单的一种方法,其基本思想就是将非线性的功能函数线性化,然后通过基本变量的一阶矩和二阶矩来计算线性化后的功能函数的一阶矩和二阶矩,进而近似得到功能函数的失效概率.由于可靠性优化设计过程中每一个迭代步都需要进行失效概率的计算,计算量巨大,为减少计算时间,本文采用均值一次二阶矩方法计算系统的失效概率.均值一次二阶矩方法是将功能函数在均值点处进行线性化展开,此时可靠性指标可以表示为:

式中,μg_MV表示功能函数在均值点处的期望;σg_MV表示功能函数在均值点处的标准差;μxi和σxi分别表示随机变量Xi的均值和标准差.
5 可靠性优化结果分析
本文多目标遗传算法采用K.Ded等在2002年提出的改进型的非劣排序遗传算法[20](NSGAⅡ).本文所选取的优化设计变量分别为一系钢簧纵/横向刚度、一系钢簧垂向刚度、转臂节点纵向/垂向刚度、转臂节点横向刚度、一系垂向减振器接头刚度、一系垂向减振器卸荷力、二系空簧纵向/横向刚度、二系空簧垂向刚度、二系横向减振器阻尼、二系横向阻尼接头刚度、二系垂向阻尼、抗蛇行减振器卸荷力、抗蛇行减振器接头刚度、横向止档间隙.根据文献[3],侧风环境下高速列车的轮重减载率Q最容易超标,其次是轮轴横向力H.而轮重减载率用来计算失效概率,因此本文选取轮轴横向力和失效概率作为优化目标,通过优化动力学参数,使目标函数达到最小.
图4给出了当车速为300km/h,风速为30m/s时,二系空簧横向刚度IXY_airspring的收敛情况.可以看出在文中所取的上下界中,经过1000次迭代,二系空簧横向刚度逐渐收敛到某个稳定的数值,并在此数值附近微幅波动.
在Pareto最优解集中可以研究设计变量与目标函数的相关性.图5分别给出了当车速为300km/h,风速为30m/s时,设计变量与目标函数的相关性,正值表示设计变量与目标函数为正相关,负值表示设计变量与目标函数为负相关.由图5可以看出,一系钢簧垂向刚度IZ_KPS、二系横向减振器接头刚度CSY_KJT、二系空簧垂向刚度IZ_airspring、抗蛇行减振器接头刚度CSX_KJT、抗蛇行减振器卸荷力CSX2和横向止档STOP_GAP与失效概率的相关性比较大.其中一系钢簧垂向刚度和横向止档与失效概率为正相关,其它的为负相关.由于在Pareto解集中,失效概率和轮轴横向力是相互矛盾的,因此设计变量与轮轴横向力的正负相关性是相反的.
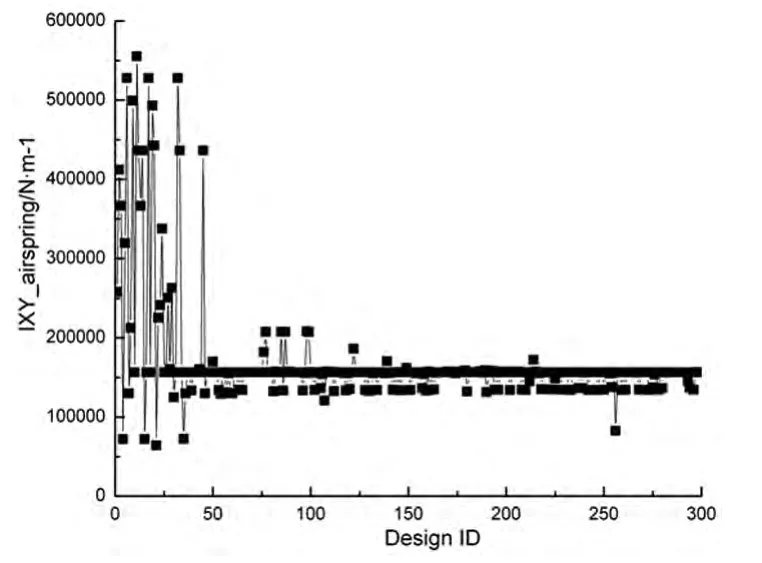
图4 设计变量的历史曲线Fig.4 The history of design parameter
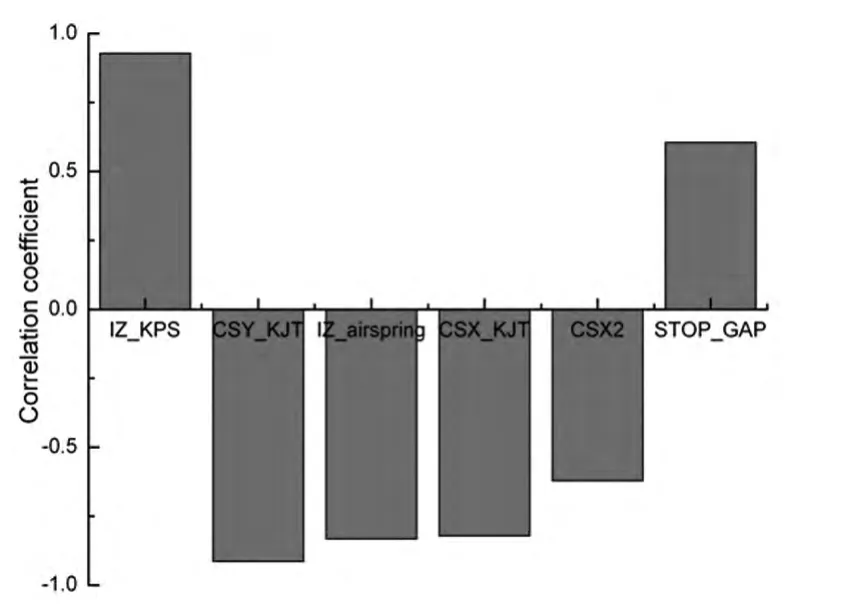
图5 设计变量与失效概率的相关性Fig.5 Correlation between X and Pf
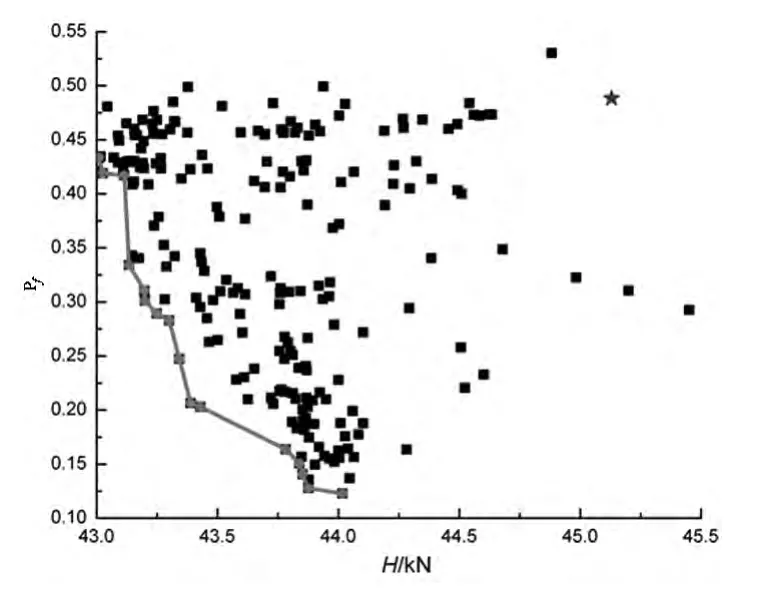
图6 Pareto前沿Fig.6 Pareto frontier
图6给出了优化设计过程中,优化目标在像空间的收敛情况,图中圆点“●”连接而成的曲线表示随机风作用下基于可靠性的高速列车动力学参数多目标优化的Pareto前沿,五角星“★”表示优化前与初始动力学参数相对应的失效概率和轮轴横向力.由图6可知,经过对高速列车动力学参数进行多目标优化设计,高速列车的失效概率和轮轴横向力得到改善,优化取得较好的效果.通过与原始动力学参数下的高速列车安全特性的对比发现,优化之后,高速列车的失效概率由原始的0.4884降低为0.1406,而轮轴横向力由原始的45.13kN降低为43.01kN.从最优Pareto前沿可以看出,失效概率和轮轴横向力是相互矛盾的,当失效概率达到最小值时,轮轴横向力的值比较大,反之亦然.
6 结论
本文基于可靠性理论计算随机风作用下高速列车的运行安全性,并基于多目标优化理论对随机风作用下高速列车动力学参数的可靠性进行优化设计,主要有以下结论:
(1)在Pareto最优解集中,一系钢簧垂向刚度和横向止档与失效概率为正相关,二系横向减振器接头刚度、二系空簧垂向刚度、抗蛇行减振器接头刚度、抗蛇行减振器卸荷力与失效概率为负相关.
(2)从最优Pareto前沿可以看出,失效概率和轮轴横向力是相互矛盾的,当失效概率达到最小值时,轮轴横向力的值比较大.
(3)经可靠性优化计算,高速列车的失效概率由原始的0.4884降低为0.1406,而轮轴横向力由原始的45.13kN降低为43.01kN.
1 马彪,丁旺才,李国芳.考虑非线性轮轨关系的高速客车横向动力学研究.动力学与控制学报,2012,10(4):329~333(Ma B,Ding W C,Li GF.Study on lateral dynamics of high-speed railway passenger car due to nonlinear wheel-rail relation.Journal of Dynamics and Control,2012,10(4):329~333(in Chinese))
2 Hoppmann U,Koenig S,Matschke G.A short-term strong wind prediction model for railway application,design and verification.Journal of Wind Engineering and Industrial Aerodynamics,2002,90:1127~1134
3 于梦阁,张继业,张卫华.平地上高速列车风致安全研究.西南交通大学学报,2011,46(6):989~995(Yu M G,Zhang J Y,Zhang W H.Wind-induced security of high-speed trains on the ground.Journal of Southwest Jiaotong University,2011,46(6):989~995(in Chinese))
4 Diedriches B,Sima M,Orellano A,et al.Crosswind stability of a high-speed train on a high embankment.Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2007,221(2):205~225
5 于梦阁,张继业,张卫华.侧风下高速列车车体与轮对的运行姿态.交通运输工程学报,2011,11(4):48~55(Yu M G,Zhang JY,Zhang W H.Running attitudes for car body and wheelset for high-speed train under cross wind.Journal of Traffic and Transportation Engineering,2011,11(4):48~55(in Chinese))
6 王永冠,陈康.横风对高速动车曲线通过性能的影响.西南交通大学学报,2005,40(2):224~227(Wang Y G,Chen K.Effects of crosswinds on curve negotiation of high-speed power cars.Journal of Southwest Jiangtong University,2005,40(2):224~227(in Chinese))
7 刘加利,于梦阁,张继业等.基于大涡模拟的高速列车横风运行安全性研究.铁道学报,2011,33(4):13~21(Liu JL,Yu M G,Zhang JY,et al.Study on running safety of high-speed train under crosswind by large eddy simulation.Journal of the China Railway Society,2011,33(4):13~21(in Chinese))
8 Wetzel C,Proppe C.Crosswind stability of high-speed trains:a stochastic approach.BBAA VI International Colloquium on:Bluff Bodies Aerodynamics&Applications,Milano,Italy,2008,20~24
9 Carrarini A.Reliability based analysis of the crosswind stability of railway vehicles.Journal of Wind Engineering and Industrial Aerodynamics,2007,95:493~509
10 杨斌,刘堂红,杨明智.大风区铁路挡风墙合理设置.铁道科学与工程学报,2011,8(3):67~72(Yang B,Liu T H,Yang M Z.Reasonable setting of wind-break wall on railway in strong wind areas.Journal of Railway Science and Engineering,2011,8(3):67~72(in Chinese))
11 李田,张继业,张卫华.横风下高速列车通过挡风墙动力学性能.铁道学报,2012,34(7):30~35(Li T,Zhang J Y,Zhang W H.Dynamic performance of high-speed train passing windbreak in crosswind.Journal of the China Railway Society,2012,34(7):30~35(in Chinese))
12 许自强,罗世辉,马卫华.速度200km/h车辆一系悬挂参数优化及性能分析.铁道机车车辆,2012,32(1):22~25(Xu Z Q,Luo S H,Ma W H.Primary suspension optimization and performance analysis on vehicle of 200km/h.Railway Locomotive&Car,2012,32(1):22~25(in Chinese))
13 杨春雷,李芾,黄运华.一系垂向悬挂对重载货车轮轨动力作用的影响.西南交通大学学报,2011,46(5):820~825(Yang C L,Li F,Huang Y H.Optimization of primary vertical suspension of heavy haul freight car.Journal of Southwest Jiaotong University,2011,46(5):820~825(in Chinese))
14 郝建华,曾京,邬平波.铁道客车垂向随机减振及悬挂参数优化.铁道学报.2006,28(6):35~40(Hao J H,Zeng J,Wu P B.Optimization of vertical random vibration isolation and suspension parameters of railway passenger car systems.Journal of the China Railway Society,2006,28(6):35~40(in Chinese))
15 廖英英,刘永强,杨绍普.高速铁道车辆悬挂系统参数化建模、优化与仿真分析.动力学与控制学报,2013,11(3):257~263(Liao Y Y,Liu Y Q,Yang SP.Parameterized modeling,optimizing and simulation analysis of suspension system for high-speed railway vehicle.Journal of Dynamics and Control,2013,11(3):257~263(in Chinese))
16 Yu M G,Zhang J Y,Zhang W H.Multi-objective design method of the high-speed train head.Journal of Zhejiang University-Science A,(Applied Physics&Engineering),2013,14(9):631~641
17 Cooper R K.Atmospheric turbulence with respect to moving ground vehicles.Journal of Wind Engineering and Industrial Aerodynamics,1985,17:215~238
18 Baker C J.The simulation of unsteady aerodynamic cross wind forces on trains.Journal of Wind Engineering and Industrial Aerodynamics,2010,98:88~99
19 于梦阁,张继业,张卫华.随机风速下高速列车的运行安全可靠性.力学学报,2013,45(4):483~492(Yu M G,Zhang JY,Zhang W H.Operational safety reliability of high-speed trains under stochastic winds.Chinese Journal of Theoretical and Applied Mechanics,2013,45(4):483~492(in Chinese))
20 Deb K,Agrawal S,Meyarivan T.A fast and elitist multiobjective genetic algorithm:NSGA-II.IEEE Transactions on Evolutionary Computation,2002,6(2):182~197

