分数阶Rayleigh-Duffing-like系统的自适应追踪广义投影同步*

张燕兰

(闽南师范大学计算机学院，漳州 363000)

引言

近来，混沌及其应用是非线性科学领域的重要研究方向之一，而混沌控制与同步是混沌理论应用的关键.混沌系统的追踪控制与同步是通过对混沌系统施加控制使受控系统的输出信号追踪先给定的参考信号的一种控制类型.参考信号可以是相空间中的某一点，也可以是混沌系统输出的混沌信号.若参考信号是混沌信号，这种追踪控制同步便演变成驱动系统和响应系统的同步.因此，追踪控制与同步是一种更广义的同步，具有很好的应用前景.

自从1983年Mandelbort指出自然界及许多科学技术领域中存在大量分数维的事实，分数阶微积分作为分形几何和分数维动力学基础的取得了很大的进展.有关分数阶混沌系统的讨论也随之迅速增加.同时，分数阶混沌系统的控制与同步也取得了一些成果，比如［1-7］.但是远没有整数阶混沌系统的控制与同步的结果丰富，有关分数阶混沌系统的追踪控制与同步的成果更少［8，9］.而分数阶混沌系统因其自身的复杂性以及参数的选择空间更大，在保密通信、信号处理等领域的应用上，要比整数阶混沌系统具有更大的密钥空间，因而分数阶混沌系统的同步更具研究价值.

广义投影同步可以获得原信号任意比例的输出信号［10］，其在数字信号保密通信中可以实现快速通信.基于以上原因，本文讨论分数阶混沌系统的自适应追踪广义投影同步.本文考虑分数阶Rayleigh-Duffing-like系统的自适应追踪广义投影同步，通过设计控制器和未知参数的辨识规则，实现含有随机扰动的分数阶Rayleigh-Duffing-like系统的自适应追踪广义投影同步.

1 分数阶Rayleigh-Duffing-like系统的自适应追踪广义投影同步

著名的Duffing方程在非线性动力学系统的研究中占有重要的地位，迄今人们对其研究方兴未艾.经典的Duffing系统有很多推广的形式，如复Duffing振子［11］，Rayleigh-Duffing振子［12］和Duffing-like振子［13］等.在文［14］中，Zhang和Luo结合Rayleigh振子和Duffing-like系统，提出了Rayleigh-Duffing-like系统(下面简称RDL系统)，并用Melnikov方法判定该系统存在混沌解.RDL系统的方程表示为

含有噪声扰动和未知参数的分数阶RDL系统为

其中0为0到α的阶Caputo微分，0＜α＜1，F未知，n(t)为高斯白噪声.我们通过设计控制器和参数辨识规则使分数阶系统(2)追踪广义投影同步参考信号(r1(t)，r2(t))，即

(σi为常数，i=1，2).先给出分数阶系统

其中X=(x1，x2，…，xn)T∈Rn，f(X，t)=(f1(X，t)，f2(X，t)，…，fn(X，t))T的平衡点稳定性的命题.引理1.1 阶数0＜α＜1的分数阶动力系统(3)是局部渐近稳定的，如果其相应的整数阶系统是稳定的［15］.

下面我们简记0为Dα.对系统(2)施加控制项u1(t)，u2(t)，则受控的分数阶RDL系统为

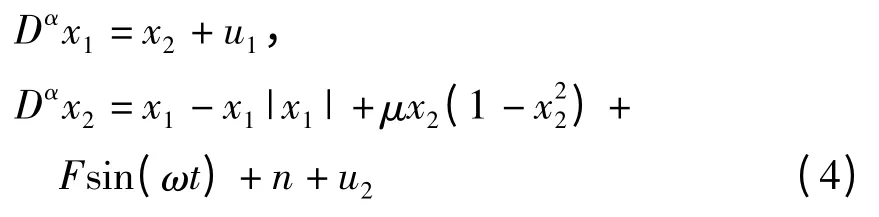
设F^为F的估计值，|n(t)|≤K.记误差.

令(4)式减(σ1Dαr1，σ2Dαr2)T，则分数阶误差系统为

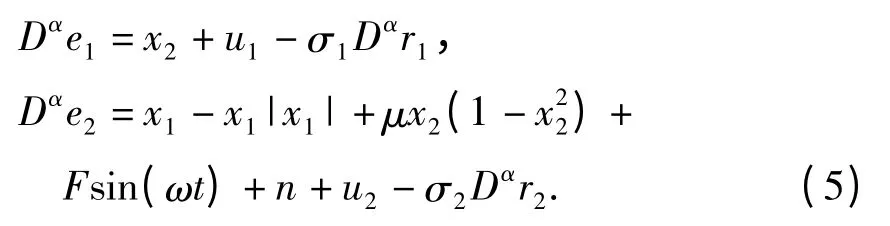
命题1.1 对分数阶RDL系统(5)，若我们选择控制规则为

以及参数更新规则:

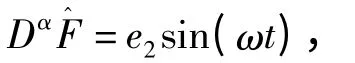
则受控的分数阶系统(4)可以追踪同步给定的信号.

证明 考虑误差系统

的稳定性.

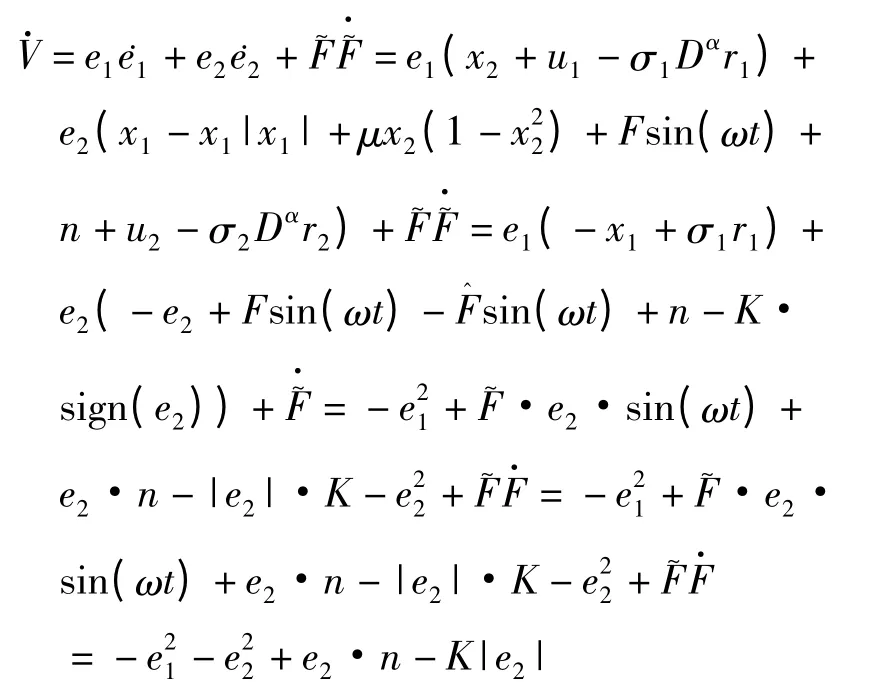
由于e2·n-K|e2|≤0，所以≤0.可见整数阶误差系统(6)稳定.根据引理1.1，误差系统(5)是渐近稳定的，则系统(4)广义投影同步给定的信号.

2 仿真

(1)第一种情况:r1=0，r2=0.在这种情况下，追踪到r1，r2相当于控制系统(2)到原点.根据命题1.1，我们取控制器为:

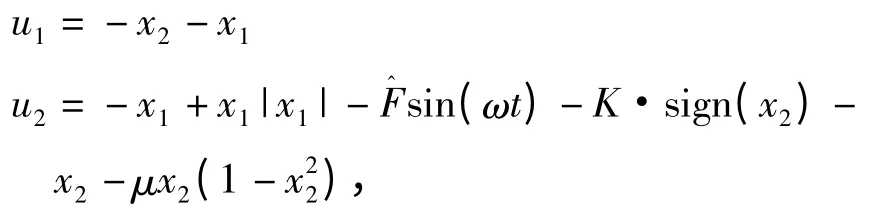
参数的更新规则为:

仿真结果:取α=0.98，μ=0.05，ω=1，F=0.4，高斯白噪声的方差为1，系统的初值为(3，-2)，(0)=0.从图1可见，x1，x2趋于平衡点，且趋于一个稳定值，可作为F的估计值.

在不改变α，μ，ω，F，高斯白噪声的方差的情况下，取系统的初值和(0)的值如下:

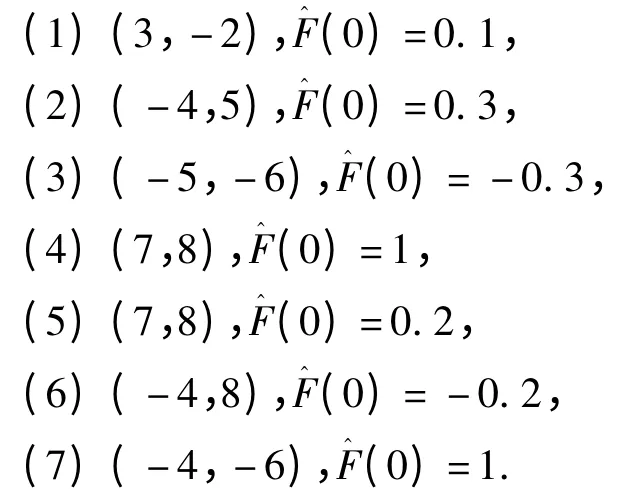
仿真结果表明，x1，x2都短时间内趋于平衡点，F的估计值都趋于0.4左右的一个稳定值.所以系统的初值和(0)的取值具有随机性，对追踪性能影响不大.

(2)第二种情况:r1，r2为分数阶混沌系统的输出信号.在这种情况下，追踪到r1，r2相当于与该分数阶混沌系统广义投影同步.

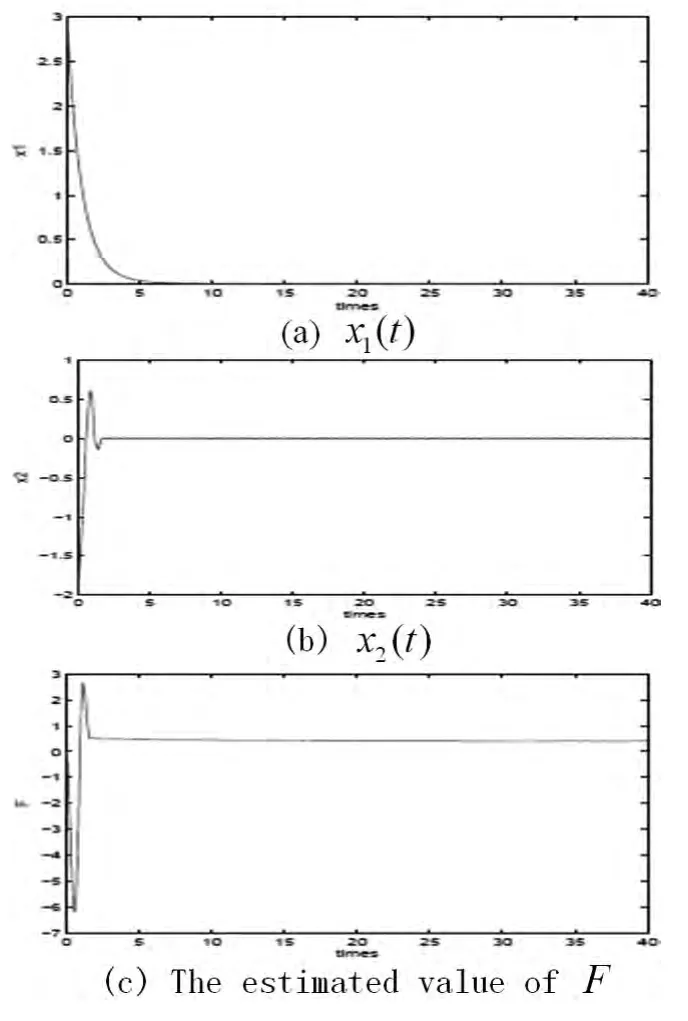
图1 系统(2)追踪平衡点Fig.1 The system(2)tracks the equilibrium

我们假设r1，r2为分数阶Duffing混沌系统的变量，即

则根据命题1.1，我们取控制器为:

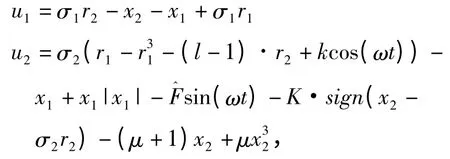
参数的更新规则为:

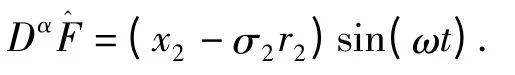
仿真结果:取α=0.98，μ=0.05，ω=1，F=0.4，l=0.5，k=0.8，σ1=-1，σ2=1，高斯白噪声的方差为1，系统的初值为(-1，1)，(0)=0.从图2可见，e1，e2趋于平衡点-0.4趋于0.

在不改变α，μ，ω，F，l，k，σ1，σ2，高斯白噪声的方差的情况下，取系统的初值和(0)的值如下:

仿真结果表明，x1，x2分别短时间内同步和反向同步于r1，r2，F的估计值都趋于0.4左右的一个稳定值.所以系统的初值和(0)的取值具有随机性，对追踪性能影响不大.

图2 系统(2)追踪分数阶Duffing混沌系统Fig.2 The system(2)tracks fractional Duffing chaotic system

如果r1，r2为分数阶RDL混沌系统的变量，即

则根据命题1.1，我们取控制器为:

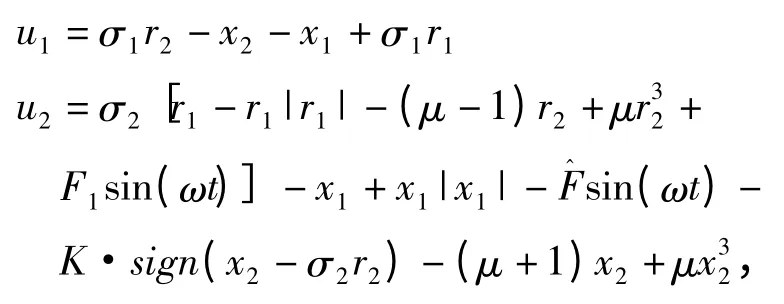
参数的更新规则为:

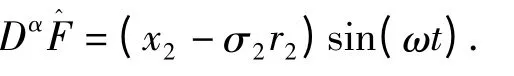
仿真结果:取α=0.98，μ=0.05，ω=1，F=F1=0.4，σ1=0.5，σ2=-1，高斯白噪声的方差为1，系统的初值为(-1，1)(0)=0.从图3可见，e1，e2趋于平衡点-0.4趋于0.

在不改变α，μ，ω，F，F1，σ1，σ2，高斯白噪声的方差的情况下，取系统的初值和(0)的值如下:仿真结果表明，x1，x2分别短时间内同步和反向同步于r1，r2，F的估计值都趋于0.4左右的一个稳定值.可见系统的初值和(0)的取值具有随机性，对追踪性能影响不大.

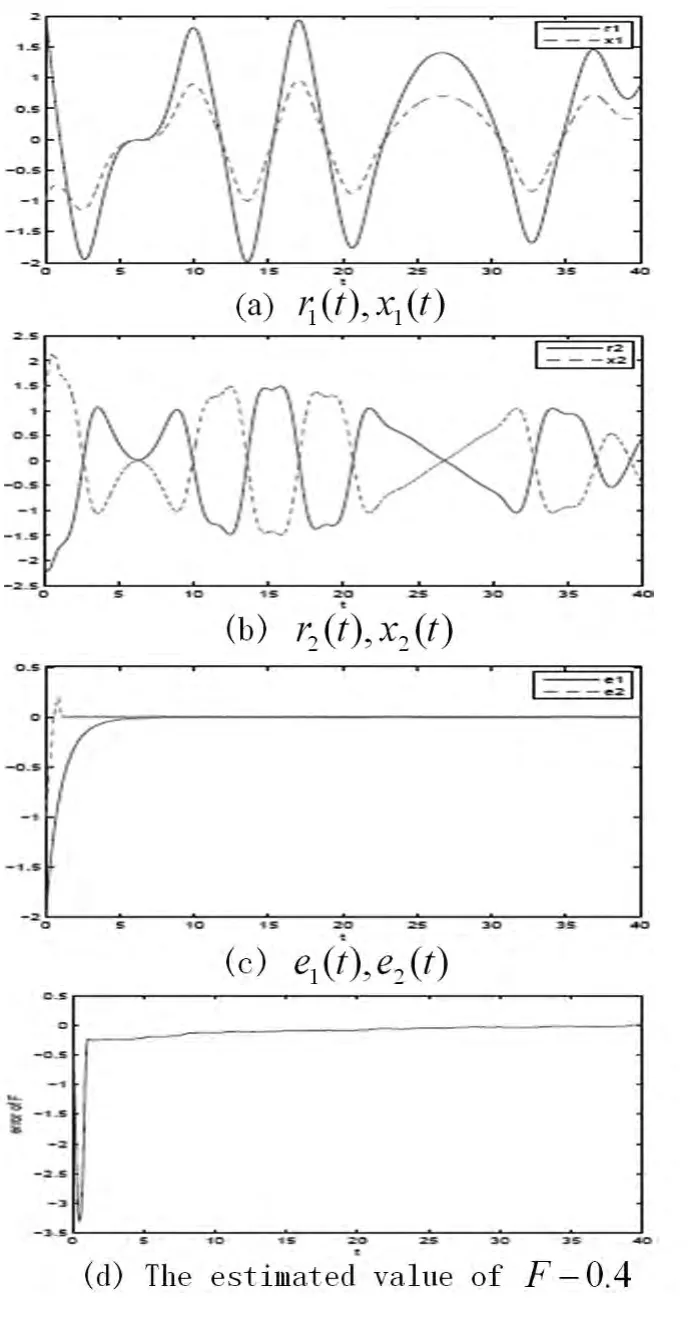
图3 系统(2)追踪分数阶RDL混沌系统Fig.3 The system(2)tracks fractional RDL chaotic system

3 结论

由于分数阶混沌系统的复杂性，分数阶混沌系统在保密通信的应用上，要比整数阶混沌系统具有更大的密钥空间.因而分数阶混沌系统的同步更具研究价值.本文通过设计控制器和未知参数的辨识规则，实现了含随机扰动和未知参数的分数阶RDL系统的自适应追踪广义投影同步;并通过数值仿真，验证了设计的控制器和参数更新规则的有效性.

1 Bhalekar S，Daftardar Gejji V.Synchronization of different fractional order chaotic systems using active control.Communications in Nonlinear Science and Numerical Simulation，2010，15:3536～3546

2 Cafagna D，Grassi G.Observer-based projective synchronization of fractional systems via a scalar signal:application to hyperchaotic Rossler systems.Nonlinear Dynamics，2012，68:117～128

3 Chen D Y，Liu Y X，Ma X Y，Zhang R F.Control of a class of fractional-order chaotic systems via sliding mode.Nonlinear Dynamics，2012，67:893～901

4 Tavazoei M S，Haeri M.Synchronization of chaotic fractional-order systems via active sliding mode controller.Physica A，2008，387:57～70

5 Wu X J，Lu H T，Shen SL.Synchronization of a new fractional-order hyperchaotic system.Physics Letters A，2009，373:2329～2337

6 黄苏海.一类分数阶四维混沌系统及其投影同步.动力学与控制学报，2011，9(2):123～130(Huang SH.A class of 4-D chaotic systems with fractional order and projective synchronization.Journal of Dynamics and Control，2011，9(2):123～130(in Chinese))

7 Binazadeh T，Shafiei M H.Output tracking of uncertain fractional-order nonlinear systems via a novel fractional-order sliding mode approach.Mechatronics，2013，23(7):888～892

8 闵富红，余杨，葛曹君.超混沌分数阶Lü系统电路实验与追踪控制与同步.物理学报，2009，58(3):1456～1461(Min F H，Yu Y，Ge C J.Circuit implementation and tracking control of the fractional-order hyper-chaotic Lü system.Acta Physica Sinica，2009，58(3):1456～1461(in Chinese))

9 赵灵冬，胡建兵，刘旭辉.参数未知的分数阶超混沌Lorenz系统的自适应追踪控制与同步.物理学报，2010，59(4):2305～2308(Zhao L D，Hu JB，Liu X H.Adaptive tracking control and synchronization of fractional hyper-chaotic Lorenz system with unknown parameters.Acta Physica Sinica，2010，59(4):2305～2309(in Chinese))

10 Yan J P，Li C P.Generalized projective synchronization of a unified chaotic system.Chaos，Solitons＆Fractals，2005，26:1119～1124

11 Mahmouda G M，Mohameda A A，Alyb SA，Strange attractors and chaos control in periodically forced complex Duffing＇s oscillators.Physica A，2001，292:193～206

12 Siewe M S，Tchawoua C，Woafo P.Melnikov chaos in a periodically driven Rayleigh-Duffing oscillator.Mechanics Research Communications，2010，37(4):363～368

13 Tang K S，Man K F，Zhong G Q，Chen GR.Generating Chaos via x|x|.IEEE Transactions on Circuits and Systems-I，Fundamental Theory and Applications，2001，48(5):636～641

14 Zhang Y L，Luo M K.Fractional Rayleigh-Duffing-like system and its synchronization.Nonlinear Dynamics，2012，70(2):1173～1183

15 Song L，Yang J Y，Xu SY.Chaos synchronization for a class of nonlinear oscillators with fractional order.Nonlinear Analysis:Theory，Methods＆Applications，2010，72:2326～2336