三种耦合RLC电路的Lagrange函数和Hamilton函数

丁光涛

(安徽师范大学物理与电子信息学院，芜湖 241000)

引言

分析力学的发展使力学理论和方法可以推广应用于其它学科领域，例如，Lagrange方程就成功地应用于电路系统和机电耦合系统，但是由于传统的Lagrange力学基本上局限于处理保守系统，故长期以来电路的Lagrange函数也只处理电感和电容线路，当涉及电阻等耗散因素时就引入耗散函数［1-5］，这种处理方法使Lagrange方程的某些优势失去，也给系统的Hamilton化增加困难.然而，电路系统的Hamilton化日益成为重要的课题，这是因为微电子学的发展使电子器件的尺度越来越小，电子电路的集成度越来越高，器件和电路的量子效应日益明显，因此介观电路的量子化问题研究提上了重要日程，而按照系统量化子的正常程序，应当先导出系统的Lagrange函数和Hamilton函数.讨论介观电路的量子效应已得到了很多成果，但是相关的研究主要讨论的是单回路电路的量子化问题，对耦合电路量子化问题的讨论则少见于文献［6-9］，因此，应当研究如何构造出耦合RLC电路的Lagrange函数和Hamilton函数问题.分析力学中变分法逆问题研究的进展使得很多耗散系统可以纳入Lagrange系统，即能够构造出这些耗散系统的Lagrange函数，并且能够进一步构造Hamilton函数［10-15］，这些耗散系统就包括通常的RLC电路.本文利用变分法逆问题的理论和方法，给出一种构造出RLC单回路电路的Lagrange函数和Hamilton函数的具体方法和程序，然后在此基础上，分别导出以电感，电容和电阻三种方式耦合的两个全同RLC回路系统的Lagrange函数和Hamilton函数.

1 单回路RLC电路的Lagrange函数和Hamilton函数

由电感L电容C和电阻R组成电路(图1)，电荷在其中运动，取电容上电量q为变量，系统的运动微分方程为

图1 RLC回路Fig.1 RLC circuit

引入如下参数

方程(1)改写成为

下面只讨论ω2大于β2这一种情况.

根据变分法逆问题理论，方程(1)或(4)不是自伴随的，不能直接表示成Lagrange方程形式［10］，我们利用变量变换可以将方程(4)变换成自伴随的，再求得Lagrange函数［15］.作变量变换

则方程(4)变换成自伴随形式的方程

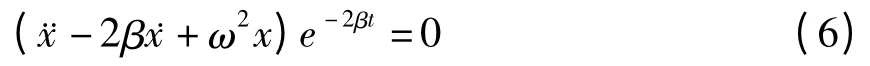
根据Engels第一方法［10，11］，直接计算得到方程(6)的Lagrange函数

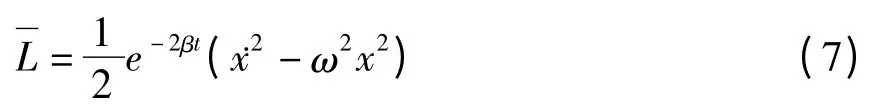
利用变换(5)，还原为原始变量q，得到

再利用Lagrange函数的规范变换化简上述函数，得到

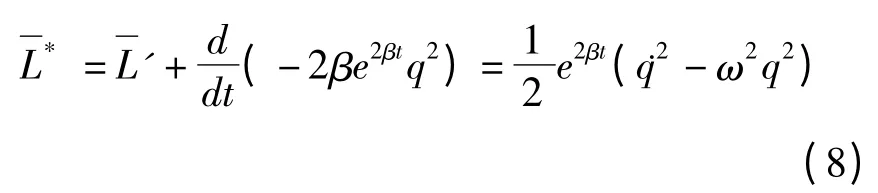
这是方程(4)的Lagrange函数.考虑到实际的RLC电路的物理意义，上述函数应当用电路的物理参数写成

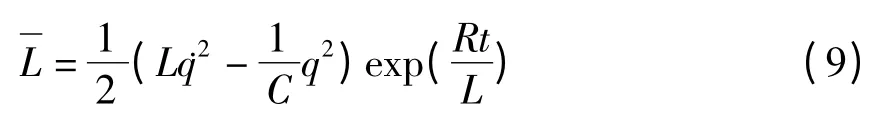
进一步利用Legendre变换得到对应的Hamilton函数.定义广义动量

则Hamilton函数为

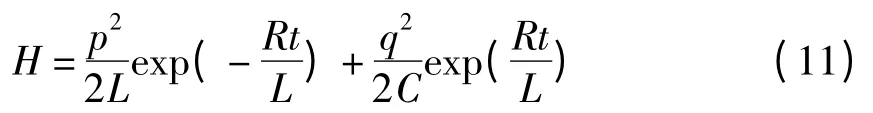
式(9)L和式(11)H就是单回路RLC电路的Lagrange函数和Hamilton函数.

2 三种耦合电路的Lagrange函数和Hamilton函数

研究两个全同回路的耦合系统的分析力学化问题，设回路的耦合方式有三种:电感耦合(图2)，电容耦合(图3)和电阻耦合(图4).

1)电感耦合电路(图2).两个RLC回路通过互感M耦合，设两个电容上的电量分别为q1和q2，则电路的微分方程为别为q1和q2，则电路的微分方程为

图2 电感耦合RL回路Fig.2 Inductively coupled RLC circuit

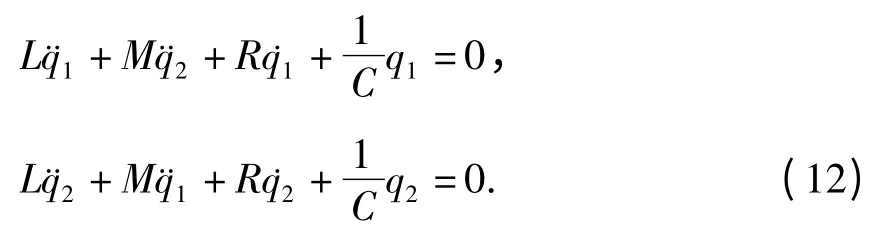
为了解除耦合，引入新变量

方程(12)变换为

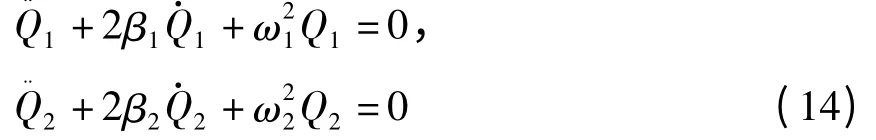
式中

显然，方程组(14)中两个方程与方程(4)形式完全相同，通过类似于上述单回路的方法步骤，可以得到方程(14)的Lagrange函数为

将变换式(13)代人上式，得到变量q1和q2表示的Lagrange函数为

用电路物理参数表示，得到电感耦合电路的Lagrange函数为

定义广义动量

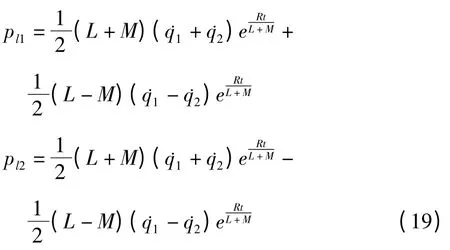
导出对应的电感耦合电路的Hamilton函数为

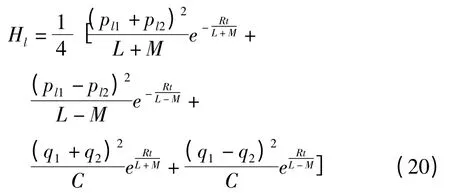
2)电容耦合电路(图3).两个RLC回路通过电容C0耦合，设两个回路的电容上的电量分别为q1和q2，则电路的微分方程为

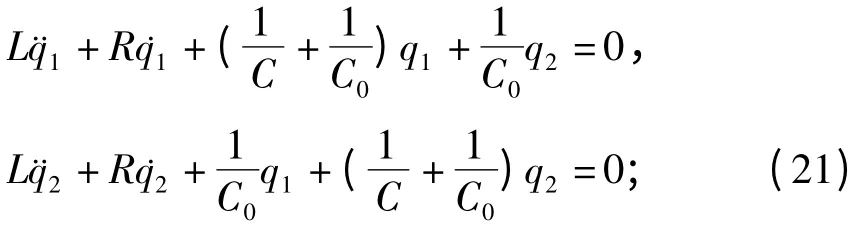
根据式(13)引入新变量，方程(21)变换成下列分离变量形式

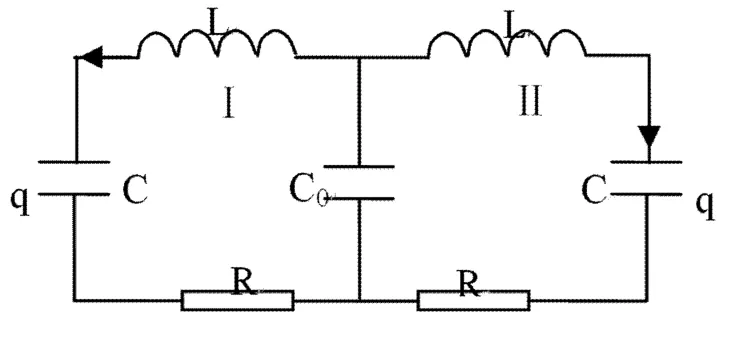
图3 电容耦合RLC回路Fig.3 Capacitive coupling RLC circuit

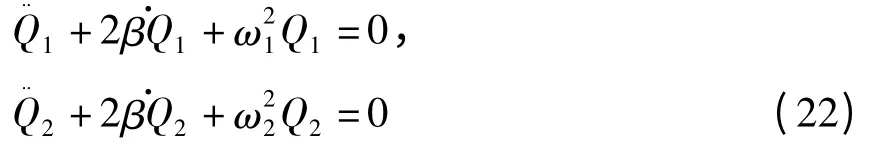
式中，

再次利用类似单回路的方法，容易得到方程(22)的Lagrange函数为

用变量q1，q2表示，则Lagrange函数写成

式中ω2=(C+C0)/LCC0=1/LC0.

用电路物理参数表示，电容耦合电路的Lagrange函数为

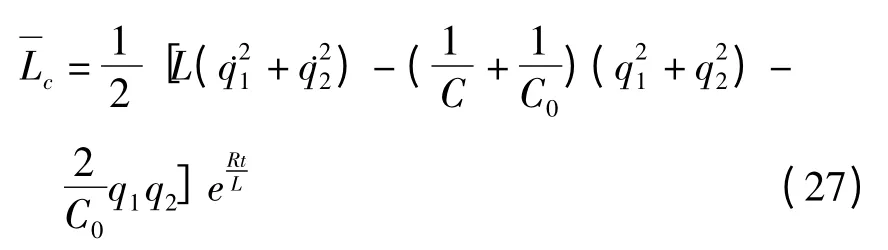
定义广义动量

则电容耦合回路的Hamilton函数为

3)电阻耦合电路(图4).两个RLC回路通过电阻R0耦合，设两个回路的电容上的电量分别为q1和q2，则电路的微分方程为

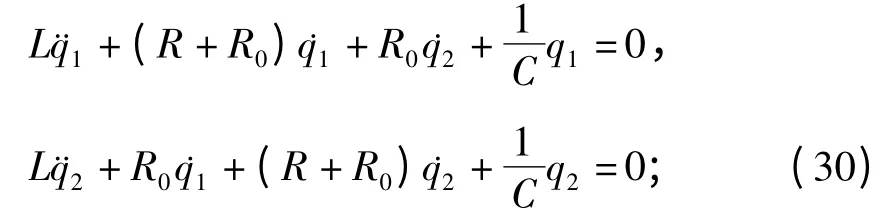
根据式(13)引入新变量，方程(30)变换成下列分离变量形式

式中

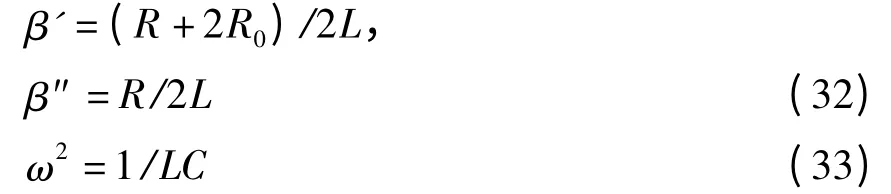
图4 电阻耦合RLC回路Fig.4 Resistance coupled RLC circuit

方程(31)对应的Lagrange函数为

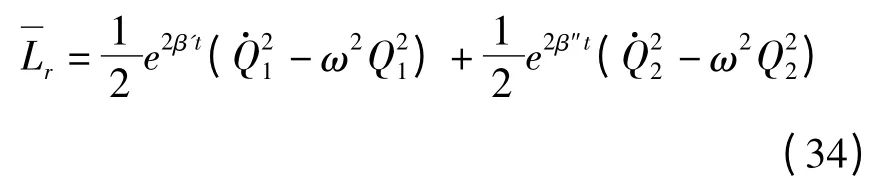
用变量q1，q2表示，则Lagrange函数写成

用电路物理参数表示，电阻耦合电路的Lagrange函数为

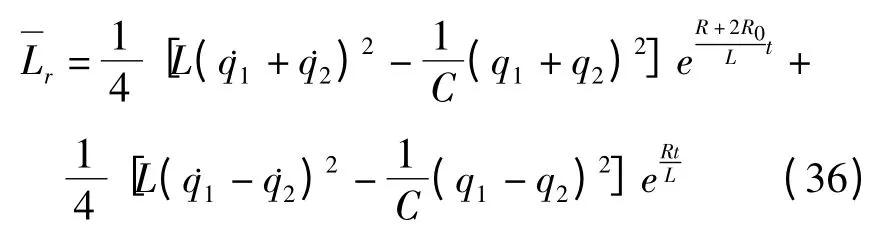
定义广义动量

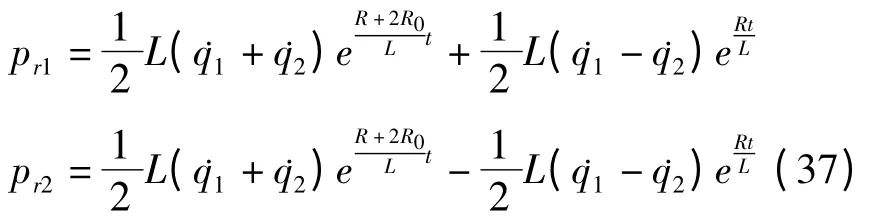
则电阻耦合回路的Hamilton函数为

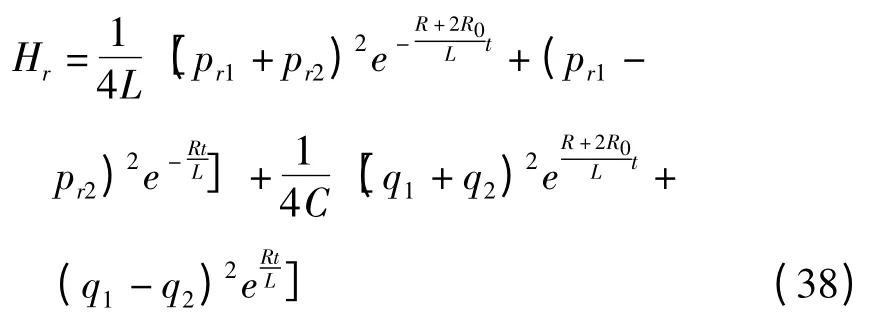
3 结论

本文首先根据变分法逆问题理论和方法，利用变量变换和规范变换构造了单回路RLC电路系统的Lagrange函数和Hamilton函数;然后，讨论由两个全同的RLC回路构成的电感、电容和电阻三种耦合系统，在解除电路微分方程中耦合项以后，再根据讨论单回路电路的方法和结果，分别构造出这三种耦合回路的Lagrange函数和Hamilton函数.值得指出的是，所得的函数形式是二次型，这是分析力学中一类重要的Lagrange函数和Hamilton函数形式，也是便于讨论系统量子化问题的形式.解决了RLC电路系统Lagrange函数和Hamilton函数的构造问题，不仅有利于用分析力学理论和方法研究经典耦合电路，而且为进一步讨论介观耦合RLC电路的量子力学问题打下了基础.

1 Goldstein H，Poole C，Safko J.Classical mechanics，3nd ed.Redwood City:Addison-Wesley，2002

2 邱家俊.机电分析动力学.北京:科学出版社，1992.(Qiu JJ.Analysis mechnanics of mechanico-electrical systems.Beijing:Science Press 1992(in Chinese))

3 Liu H J，Tang Y F，Fu JL.Algebraic structure and Poissom’s theory of mechanico-electrical systems.Chinese Physics，2006，15:1653～1661

4 Li Y C，Xia L L，Liu B，Jiao Z Y，Wang X M.Unified symmetry of mechano-electrical systems with nonholonomic constraints.Chinese Physics B，2008，17:1545～1749

5 Huang W X，Wang Q J，Yin X G，Huang CP，et al.Optical resonance in a composite asymmetric plasmonic nanostructure.Journal of Applied Physics，2011，109:114310

6 龙超云，刘波.轻阻尼RLC量子化回路的双波描述.物理学报，2001，50(6):1011～1014(Long C Y，Liu B.Double-wave function of RLCcircuit after quantization.Acta Physica Sinica，2001 50(6):1011～1014(in Chinese))

7 汪仲清.介观RLC电路在热真空态下的量子涨落.物理学报，2002，51(8):1808～1810(Wang Z Q.Quantum flunctuation in thermal vacuum state for mesoscopic RLC circuit.Acta Physica Sinica，2002，51(8):1808～1810(in Chinese))

8 Xu C L.Number-phase quantization of a mesoscopic RLC circuit.Chinese Physics B，2012，21:020402

9 刘清，邹丹，嵇英华.交流源作用下介观RLC电路系统量子态随时间的演化.物理学报，2006，55(4):1596～1601(Liu Q，Zou D，Ji Y H.Time evolution of mesoscopic RLCcircuit driven by an alternating current source.Acta Physica Sinica，2006，55(4):1596～1601(in Chinese))

10 Santilli R M.Foundations of theoretical mechanicsⅠ.New York:Spinger-Verlag，1978

11 Santilli R M.Foundations of theoretical mechanicsⅡ.New York:Spinger-Verlag，1983

12 Cie s＇liński J L，Nikiciuk T.A direct approach to the construction of standard and nonatandard Lagrangians for dissipative-like dynamical systems with variable coefficients.Journal of Physics A:Mathemetical and Theorems，2010，43:17250

13 丁光涛.从运动方程构造Lagrang函数的直接方法.动力学与控制学报，2010，8(4):305～310(Ding G T.A direct approach to the construction of Lagrangians from the motion equation.Journal of Dynamics and Control，2010，8(4):305～310(in Chinese))

14 丁光涛.一维变系数耗散系统Lagrange函数和Hamilton函数的新构造方法.物理学报，2011，60(4):044503(Ding G T.A new approach to the construction of Lagrangians and Hamiltonians for one-dimensional dissipative systems with variable coefficients.Acta Physica Sinica，2011，60(4):044503(in Chinese))

15 丁光涛.利用变量变换构造耗散系统Lagrange函数.动力学与控制学报，2012，10(3):199～201(Ding GT.The construction of Lagrangians for dissipative-like systems by using the transformations of variables.Journal of Dynamics and Control，2012，10(3):199～201(in Chinese ))