基于径向基函数神经网络和无迹卡尔曼滤波的弹丸落点预报方法研究

赵捍东，李志鹏

(中北大学 机电工程学院，山西 太原030051)

0 引言

弹丸落点的精确快速预报对实施弹道修正进而实现精确命中至关重要。然而在实际应用中面临的问题是，弹载计算机处理能力有限，解算过程允许耗时较短，且弹载传感器输出数据较真实值有一定偏差，这就要求落点预报算法要有较好的实时性、准确性、容错性。当前的预报方法中以数值积分法、滤波外推法等较为常见。数值积分法的实质在于使用龙格库塔法对外弹道方程组进行求解，解算精度依赖弹载计算机的性能和解算步长、不易实时修正相关系数，而且弹丸飞行过程中受到随机风、科氏力等诸多因素的影响［1-2］，尤为突出的是数值积分法容错机制不佳。滤波外推法是基于最小均方差理论的递推预报方法，具有一定的容错能力，但其理论基础是建立在线性系统和高斯噪声环境上的，用于飞行弹道这一非线性系统时不可避免地会产生一定误差，当噪声为非高斯复杂噪声时甚至引起滤波发散。国内外学者也曾尝试通过对弹道方程进行多元逼近来解决这些问题，但多元函数的数学逼近一般以多元剖分法为主，对弹道方程组逼近精度不足，且其建立在较深的数学知识的基础上，难以为一般学者掌握。

出于这些原因，本文提出了一种使用神经网络对外弹道方程进行逼近来预报弹丸落点的方法。神经网络是模仿人脑进行信息处理的一种智能方法，具有出色的非线性处理能力和容错能力。而在众多的神经网络类型中，径向基函数(RBF)神经网络是建立在基函数逼近理论上的一种神经网络，所以具有比其他网络更好的全局逼近能力和最佳逼近能力［3］。根据函数逼近理论，任何函数都可以表示成一组RBF 的加权和。而RBF 神经网络的拓扑结构则可以通过权值阈值和基函数中心的调整来实现对不同基函数的加权组合，进而实现对目标函数的逼近。从而实现这样的映射关系:Γ∶ x→y，其中，x∈Rn，y∈Rm，x 和y 分别为输入向量和输出向量，Rn和Rm分别表示n 维和m 维实数空间。那么当自变量x 为弹丸的飞行数据且因变量y 为弹丸的落点信息时，通过RBF 神经网络即可实现由飞行数据对落点信息的映射。同时，RBF 神经网络对多元函数的逼近能力也得到了充分的证明［4］。RBF 神经网络在弹丸落点的预报中，由于采用了并行结构，且没有繁琐的迭代过程，所以具有解算时间短的优点，有利于落点预报的快速实现。但其缺陷在于逼近精度依赖于网络结构和训练方法。传统的RBF 网络的训练方法主要有K-means 方法和梯度下降法等，但这些训练方法容易导致局部最优和结构冗余，所以本文采用了能够收敛于全局最优的量子行为粒子群优化(QPSO)算法对其进行优化，并引入了滤波算法以减小模型误差。

1 落点预报

1.1 基于RBF 神经网络的落点预报

根据文献［1 -2］可知，对于任一组弹丸飞行数据向量I=(x，y，z，vx，vy，vz，a，φ，φ)，分别表示当前位置三分量，速度三分量，轴向加速度，偏航角，俯仰角，在弹道不进行机动的情况下对应唯一一个落点。记落点信息在惯性坐标系中的向量表示为O =(X，Z)，即射程和横偏。那么必然存在这样的方程:

即射程和横偏量是关于当前飞行数据的函数(注:F不是指6 自由度外弹道方程组)。只需求出这样的函数，使得(1)式形式的方程恒成立，即可根据当前飞行数据实时求解落点信息。(1)式形式的函数为一超曲面函数，不易求得精确的初等表达式。本文试图找到这样一种映射Γ(·)，实现对(1)式的无限逼近，即对于任意第i 组飞行数据Ii=(xi，yi，zi，vxi，vyi，vzi，ai，φi，φi)，都能够使得

成立，那么此映射即可以用于快速解算弹丸落点信息。基于这个思路，本文引入了RBF 神经网络方法来解决这个问题。

RBF 神经网络是在借鉴生物交叠接受区域知识的基础上提出的一种神经网络［3］。在众多的神经网络中，RBF 神经网络结构简洁、稳定性好，是具有输入层、隐含层、输出层的3 层前向神经网络。其中输入层到隐含层执行非线性变换，隐含层到输出层执行线性加权运算。由于隐含层上的激励函数采用了RBF，可使得网络具有很好的局部逼近能力［4］。RBF 神经网络的拓扑结构如图1所示。

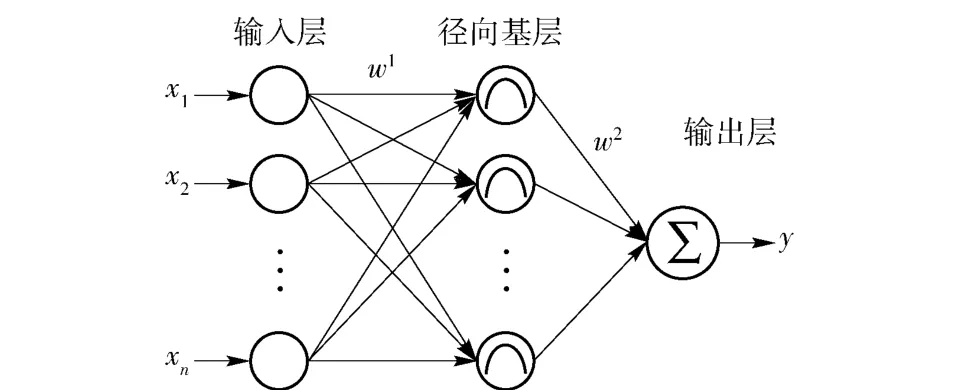
图1 RBF 神经网络拓扑结构图Fig.1 Topology structure of RBF neural network

令(Ii，Oi)表示由飞行数据和落点信息构成的欧氏空间中的点，并且(Ii，Oi)共有N 个，则可以使用函数Γ 对这N 个点进行插值以实现对F 的逼近。当N 足够大，且网络的结构和激励函数合理时，可实现对任一函数的高精度的逼近［5］，即可实现Γ 的功能。

不同于其他前向神经网络的是，RBF 神经网络并不事先确定隐层神经元数，一般方法是在训练过程中，经对样本的动态聚类来确定隐层神经元数。所谓动态聚类，是指在训练过程中，对整体训练样本基于动态聚类算法进行分类，每一组聚类后的子样本集构成一个单元，即可认为是一个神经元。可见，在样本完备且适定的情况下，原函数所表达的每一种情况都可以包括在内，那么经神经网络对原函数F 的逼近就是精确的。经合适的训练之后，网络的输入输出关系可表达为

式中:x、y 分别为神经网络的输入向量和输出向量;w 为权值，上标表示权值所处的层数，下标表示参与连接的神经元编号;b 为相应神经元上的阈值;‖·‖表示欧氏范数［4，6］;xi表示输入层第i 个神经元上的输入值。经训练确定网络的结构、权值和阈值后，即可在网络中形成智能映射Γ，实现从I 到O的映射。

作为一种监督式学习网络，RBF 神经网络在学习中确定隐层单元数和权值阈值，如前所述，一般的RBF 训练方法为动态聚类算法，但这种方法的聚类数不易确定，以致不能完全表现出RBF 网络的优越性。为此，本文引入粒子群优化(PSO)算法进行RBF 神经网络的训练。

1.2 RBF 训练方法的改进

PSO 算法通过群体中粒子间的协作与竞争来搜索全局最优解［7-8］。在实际应用中，每一个粒子代表一个待求量的可能解，每个粒子通过以下规则实现寻优:

式中:vk+1i，j为第i 个粒子第j 维当前前进的速度;xk+1i，j为第i 个粒子第j 维粒子的当前位置;pi，j、pg，j分别表示粒子的个体最优位置和全局最优位置;r 为随机常数;c 为学习因子;w 为惯性权重。

将PSO 方法用于RBF 神经网络的训练时，其目的在于求得最佳的神经元数和最优的权值和阈值［6-7］。那么这些粒子就可以认为是待定的神经元中心数、权值和阈值大小，而粒子的当前位置就可以认为是这些待定参数的当前值。即

不妨将其看作是一组向量，而找到的最优“位置”即为对向量中的元素最优解，也就是神经网络的最佳权值和阈值。

PSO 虽然是一种高效的全局寻优算法，但是也存在一定的缺陷。比如算法容易早熟，搜索空间不能够覆盖整个可能的解空间等。这样训练RBF 神经网络时，相关参数便不能得到全局最优解。为了利用PSO 的优点，且避开其典型缺陷，本文使用改进型量子行为粒子群优化(IQPSO)算法进行网络训练。与PSO 相比，该算法模型更简单，协同能力更强，极大增强了全局搜索能力［8-10］。IQPSO 在进化搜索过程中舍去了传统PSO 中的速度更新部分，并在传统PSO 的基础上引入了势点p 的概念［8］。p 点表示每个粒子收敛的随机点，是对量子行为思想的体现。其中

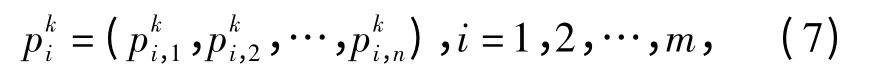
式中:m 表示粒子的个数;n 表示每个粒子的维数;k表示第k 次迭代。

同时定义:

式中:pi，j表示粒子个体最佳位置;全局最佳位置pg的下标即为(8)式中的g;a 是0 ～1 之间的随机系数;f(·)是表征在优化的作用下目标函数输出性能的函数，这里称之为适应度函数。结合弹丸落点预报的需求，本文定义f(·)表征神经网络的映射能力的优劣，即

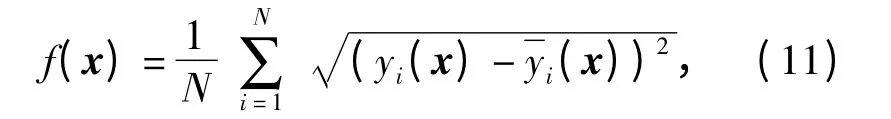
式中:N 表示输出层神经元数。(11)式的含义为对应于待定参数x 的神经网络的实际输出与理论输出的偏差量。这时，粒子位置的表达形式为

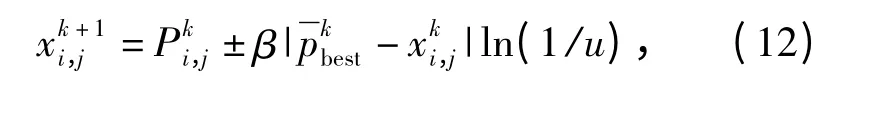
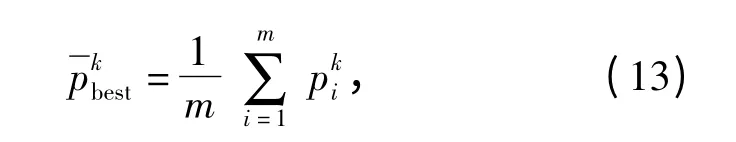
式中:u 为0 ～1 之间的随机数，当u≥0.5 时，±取-号，否则取为+号表示当前粒子群的平均最优位置;β 为速度系数。实际应用中发现，系数β 会影响粒子群的收敛性能。为此文中取β 为自适应变量［10］，即

式中:kmax表示最大迭代次数。同时将(13)式改进为

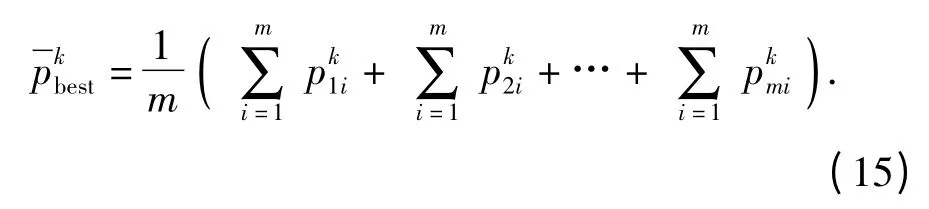
那么，选取样本，并定义误差函数后，即可使用IQPSO 算法对神经网络进行训练，即对所有待定参数寻求最优解。其算法流程如图2所示。

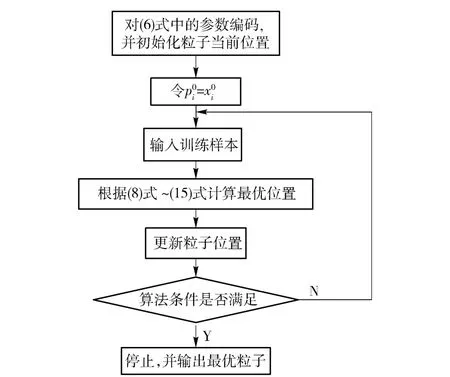
图2 IQPSO 算法优化RBF 神经网络流程Fig.2 Flow chart of optimizing RBF neural network with IQPSO

2 数据处理

使用RBF 神经网络对弹道方程进行插值逼近时，理论上可以无限逼近，由于训练样本不可能真正完备且适定，并且即使采用了改进的参数优化算法确定网络的结构和权阈值，也只是在RBF 神经网络的基础上对已知样本点的空间点进行插值逼近，与真实外弹道方程仍有一些误差。为此，本文引入滤波算法来消除一步预报值的误差。由于无法判知RBF 神经网络一步预报落点信息的偏差所服从分布的类型，所以使用适用于非线性系统和非高斯噪声环境的无迹卡尔曼滤波(UKF)算法对初步的预报结果进行去噪处理。

UKF 区别于卡尔曼滤波和最小二乘滤波之处在于，在求最佳增益矩阵时，UKF 根据观测量和协方差来确定最佳增益矩阵［11］，并根据状态向量均值和方差阵复现出2n+1 个σ 样本点，实现系统状态变量的近似分布［12］。令待求状态向量表示为X，量测向量表示为Z，状态向量和观测向量是同维的，表示为n，这里观测向量即可认为是神经网络的一步预报输出结果。令状态向量X 的均值和方差表示为和PX，那么按照无迹变换(UT)，可取得在X 周围的2n+1 个σ 点为

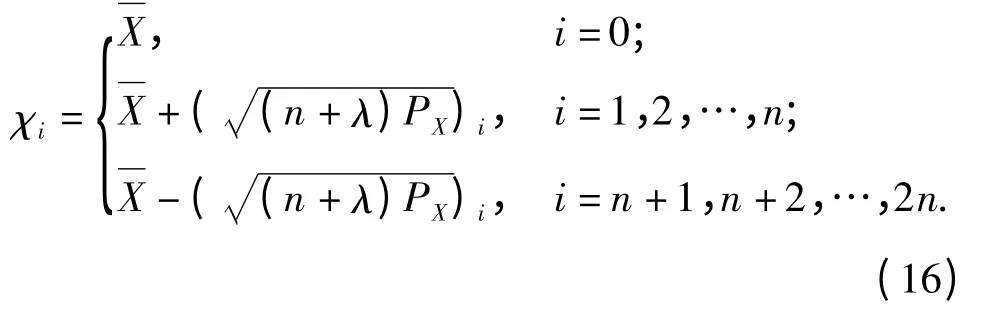
式中:λ=α2(n +κ)-n，同时定义与χi对应的权值为

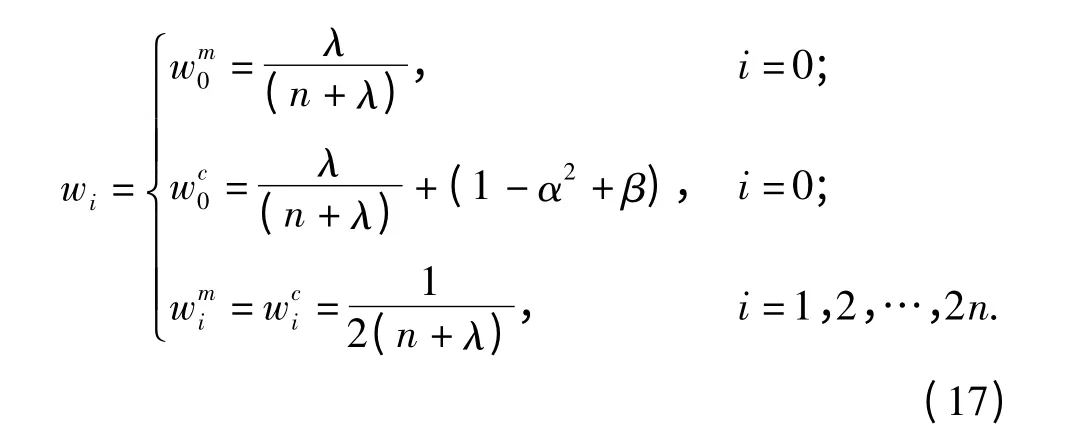
式中:α 用于调节σ 点和X 的距离，通常取大于0 的小数;β 是包含了X 的分布信息的加权系数;κ 是为保证方差阵半正定而设置的次要参数［11-12］。不失一般性，设状态方程和观测方程分别为

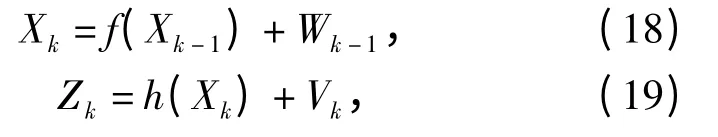
式中:W、V 分别为状态噪声和量测噪声;k 表示第k次观测，那么对状态向量的滤波迭代更新过程可表示为

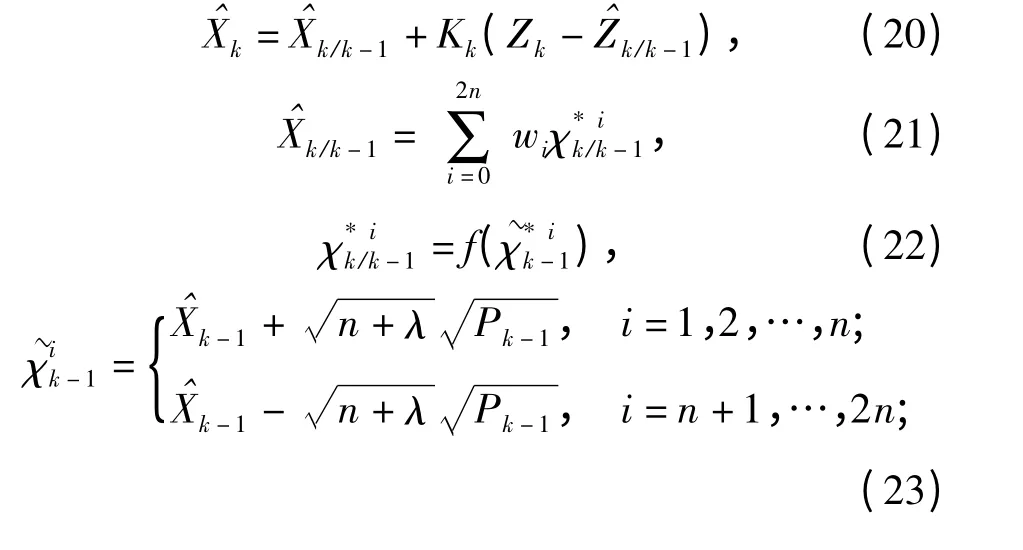
3 仿真与分析

3.1 落点预报仿真

训练样本对网络的逼近精度和泛化能力有很大影响。样本选取时，在每条弹道上，提取对应于前文(x，y，z，vx，vy，vz，a，φ，φ)的飞行数据和与此相对应的(X，Z)值。神经网络的输入量即为(x，y，z，vx，vy，vz，a，φ，φ)，输出量为(X，Z).这样的输入量可以用较少的参数比较完善地表达弹丸飞行特性。而且经验表明，这样的样本组合可以比其他形式的样本组合获得更好的预测精度。在实际应用时，这些输入量数据可以通过弹载的GPS/惯性测量单元，或GPS/惯性测量单元/地磁测量单元获得比较精确的值，数据获取也较为容易。

为保证样本的适定性，本文采用这样的方法选取训练样本:基于6 自由度弹道方程，使用4 阶龙格库塔法，设定解算步长为0.01 s，解算出弹道数据作为备选飞行数据，从5° ～60°的射角范围内，每隔2°提取一条弹道，从出炮口5 s 开始每隔2 s 采集一次飞行数据，至落地前5 s 结束，作为初级样本，记为A.确定初级样本A 后，基于模糊聚类和因子分析的方法对样本A 进行优化，使训练样本分布更均匀且更具有“代表性”，避免某类样本过多致使网络过拟合和某类样本过少而致使网络欠拟合，最终影响网络的泛化能力和逼近精度。选取出合适的样本后，基于IQPSO 对RBF 神经网络进行训练优化。以顺序方式输入样本进行训练，得到训练过程中网络的理论输出值和实际输出值之间误差的变化曲线，如图3所示。

图3 IQPSO 优化RBF 神经网络的误差收敛曲线Fig.3 The convergence curve of the error of IQPSO optimizing RBF neural network

从图3中可以看出，训练到300 次以后，随着训练样本的输入，网络的期望输出与实际输出之间的差值逐渐变小，并最终趋于稳定，即各参数已达到最优解的某邻域内，也即说明IQPSO 优化神经网络是全局收敛的。从训练误差变化曲线中可以看出，随着训练的进行，误差达到了0.000 1 的精度，说明收敛精度较好，而对应于本次训练，训练时间为12.4 s，收敛速度也较好。

取自同一弹种而未录入训练样本的飞行数据作为测试样本对训练完毕的网络进行测试，输入量为测试样本中对应的(x，y，z，vx，vy，vz，a，φ，φ)值。仿真预报时对测试样本加入由高斯噪声和厚尾噪声组合的复杂噪声。考虑到实际测量时，加速度误差和姿态角误差数值较小，所以对加速度信息添加其真实值1.5%的噪声，均值为0，统计方差为0.35;对俯仰角和偏航角添加其真实值2%的噪声，均值为0，统计方差分别为0.5 和0.6;实际应用中速度测量误差一般不大于5 m/s，位置测量误差一般不大于15 m，文中对速度信息和位置信息添加均值为0，方差分别为5 和15 的噪声，约占其真实值的1%和0.3%.每隔0.2 s 输入一次飞行数据，对每次一步预报数据进行滤波处理，设定前后两次滤波输出差值小于2 m 时输出结果。测试时，设定瞄准点为15 ～20 km，每隔100 m 测试一次。记录每条弹道上经神经网络预报的落点信息的最大误差与经滤波后的最终预报落点信息，与实际落点比较，统计出射向和横向上的偏差值，如图4和图5所示。

每次测试时从出炮口10 s 后开始采集飞行数据作为测试的输入。最多解算次数27 次，即跟踪弹道时间5.4 s，最少解算次数8 次，即跟踪弹道时间1.6 s，后续预报弹道长度为10 ～16 km.分析预报数据可知，由于测试数据具有输入噪声，经神经网络输出的一步预报数据，射向最大预报误差为132 m，横向最大预报误差为53 m，并且射向和横向的预报数据均有误差。经滤波处理后，射向误差最大为10.2 m，最小误差为0 m，横向最大误差为8.4 m，最小误差为0 m，即误差控制在了较小的范围内。

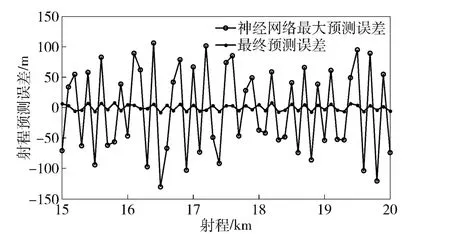
图4 射程方向预报偏差统计Fig.4 Range direction prediction bias statistics

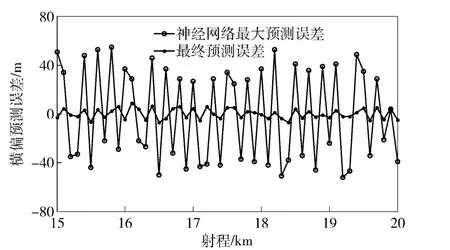
图5 横偏方向预报偏差统计Fig.5 Side direction-of-arrival prediction bias statistics

3.2 仿真与统计分析

为了对比本文方法与传统方法预报效果的异同，在15.5 km、16.5 km、17.5 km 射程的弹道数据上，加入前文所述噪声，分别用数值积分法和滤波外推法预报弹丸落点，此时设定数值积分步长、外推步长均为0.05 s，飞行数据输入间隔设定为0.1 s，出炮口10 s 时开始输入飞行数据。分别统计其落点解算信息，如表1所示。

从表1中可以看出，在飞行数据有复杂噪声时，数值积分法解算精度最差，由于其在计算机上解算时进行繁复的循环迭代，其解算时间较长;滤波外推法解算精度较数值积分方法有所提高，但其在外推之前有计算方差的时间，即弹道跟踪时间，使得其解算时间较数值积分法长，但实际测量噪声较简单时，弹道跟踪点数会减少从而减小总体解算时间;本文方法在解算精度与解算时间上均有优势，也就是说，当输入量为完备的(x，y，z，vx，vy，vz，a，φ，φ)值时，在神经网络中很好地形成了由飞行信息到落点信息的非线性映射。

表1 不同方法的落点预报统计Tab.1 The statistics of impact-points predicted by various methods

如图1所示，RBF 神经网络采用了并行结构，其计算原理从根本上区别于冯诺衣曼计算机原理，而是对数据采用并行处理的方式，实际应用时可以节省大量解算时间。滤波过程又对预报数据进行了去噪处理，所以可以获得较高的精度，使得本文方法具有良好的容错性和实时性。当实际工作中输入数据噪声较为简单时，滤波次数将会大幅减小，解算耗时会更短。但本文方法的解算精度依赖于样本的精确性，因为样本的精度决定了逼近误差的大小，如果实际使用时训练样本误差较大，预报误差会较大。实践表明，使用神经网络方法进行落点预报时，若神经网络输入层数据不完整，预报结果会产生较大误差。同时，因神经网络的性能依赖于训练样本，所以通用性不佳，如155 mm 口径弹丸的飞行数据训练的网络不能用于125 mm 口径弹丸落点的预测。对于这类问题，将网络训练完毕后提取出其数学模型，并设置根据不同弹种变化的自适应参数，是解决这个问题的一种方法，也是今后工作的方向。

4 结语

为了快速高精确地实现落点预报，本文引入了RBF 神经网络方法，并使用IQPSO 来获取所需神经网络的参数，然后在此基础上对预报数据进行滤波处理，最后进行了仿真。仿真结果表明:IQPSO 的RBF 神经网络逼近精度高，训练误差达到了0.000 1的精度级别，收敛速度较快;基于RBF 神经网络和无迹卡尔曼滤波的方法预报弹丸落点具有良好的容错性，当输入数据具有复杂噪声时，最大预报误差为10.2 m，最小预报误差0 m.说明本文提出的方法对飞行数据不尽准确的情况下进行的落点预报是有效的，为弹丸落点预报的实际应用提供了一种参考。

References)

［1］ 杨绍卿.火箭外弹道偏差与修正理论［M］.北京:国防工业出版社，2011:20 -30.YANG Shao-qing.The trajectory error and correction theory of rocket［M］.Beijing:National Defense Industry Press，2011:20 -30.(in Chinese)

［2］ 柏杰锋，王晓鸣，李文彬.CCD 与MEMS 组合测量弹丸落点偏差的方法［J］.系统仿真学报，2009，21(2):599 -604.BAI Jie-feng，WANG Xiao-ming，LI Wen-bin.Combined measuring method and simulation of deviation［J］.Journal of System Simulation，2009，21(2):599 -604.(in Chinese)

［3］ 侯媛彬，杜京义.神经网络［M］.西安:西安电子科技大学出版社，2007:128 -138.HOU Yuan-bin，DU Jing-yi.Neural network［M］.Xi’an:Xidian University Press，2007:128 -138.(in Chinese)

［4］ 隆金玲.Sum-of-Product 神经网络和径向基函数神经网络逼近能力研究［D］.大连:大连理工大学，2008.LONG Jin-ling.Approximation capability of sum-of-product neural networks and radial basis function neural networks［D］.Dalian:Dalian University of Technology，2008.(in Chinese)

［5］ 段晓君.神经网络的函数逼近能力分析［J］.模糊系统与数学，1998，24(4):80 -84.DUAN Xiao-jun.Analysis on neural network capability of approximation to function［J］.Fuzzy System and Mathematics，1998，24(4):80 -84.(in Chinese)

［6］ Fathi V，Montazer G A.An improvement in RBF learning algorithm based on PSO for real time applications［J］.Neurocomputing，2013，111(2):169 -176.

［7］ Tsekouras G E.A simple and effective algorithm for implementing particle swarm optimization in RBF network＇s design using inputoutput fuzzy clustering［J］.Neurocomputing，2013，108(2):36 -44.

［8］ Su X，Fang W，Shen Q，et al.An image enhancement method using the quantum-behaved particle swarm optimization with an adaptive strategy［J］.Mathematical Problems in Engineering，2013，2013(1):1 -14.

［9］ Sun J，Fang W，Palade V，et al.Quantum-behaved particle swarm optimization with Gaussian distributed local attractor point［J］.Applied Mathematics and Computation，2011，218(7):3763 -3775.

［10］ Xi M，Sun J，Xu W.An improved quantum-behaved particle swarm optimization algorithm with weighted mean best position［J］.Applied Mathematics and Computation，2008，205(2):751 -759.

［11］ Rhudy M，Gu Y，Napolitano M R.An analytical approach for comparing linearization methods in EKF and UKF［J］.International Journal of Advanced Robotic Systems，2013，208(10):1-9.

［12］ 吴小文，李擎.UKF 在MEMS 陀螺随机噪声补偿的应用［J］.火力与指挥控制，2013，38(6):8 -10.WU Xiao-wen，LI Qing.Research on application of UKF to compensation of MEMS gyro random noise［J］.Fire Control ＆ Command Control，2013，38(6):8 -10.(in Chinese)