一类p-Laplacian方程周期解的存在唯一性
严树林,李志艳,葛渭高
(1.常州工程职业技术学院基础部,江苏常州213164)(2.河海大学常州校区数理部,江苏常州213022)(3.北京理工大学数学学院,北京100081)
近年来,二阶微分方程周期解的存在性得到了广泛研究[1-10]。最近,有学者研究了带 p-Laplacian算子的微分方程周期解的存在性及唯一性.例如,文献[4]中研究了方程 (φp(x′))′+f(t,x′)+g(t,x)=e(t),得到了一些好的结果.受文献[4]的启发,文中进一步研究一类更广泛的二阶p-Laplacian方程的周期解,其中φp(u)=|u|p-2u,p > 1,f(t,·,·)关于t是周期为T的连续函数,e是周期为T的连续函数,显然文献[3]是本文的特例.文中推广和改进了已有文献的结果.

1 主要引理
对于周期边值问题

式中:f∈ C(R3,R).为方便起见,记.下面的引理1是文中的重要依据.
引理1[7]假设 Ω 是中的有界开集且下列条件满足
(A1)对于 ∀λ ∈(0,1),方程(φp(x′(t)))′=λ~f(t,x,x′),x(0)=x(T),x′(0)=x′(T)在∂Ω上无解;
(A2)定义函数满足F(r)F(-r)<0,其中r>0.
对于 t∈ (0,T0),有 |y(t)|≤ D,其中
为行文方便,列出下列假设,在第2节中,它们将被用来研究方程(1)的T-周期解.
[H1]假设存在常数 d > 0,使得 f(t,x0,0)>|e|0,∀x0> d;
[H2]假设存在常数 d > 0,使得 f(t,x0,0)<-|e|0,∀x0<-d;
[H3]f有分解式 f(t,x,x′)=g(t,x)+h(t,x,x′),其中 g,h 分别满足 x[g(t,x)+h(t,x,0)-e(t)]> 0,当x ≥d时;h(t,x0,x1)≤m1|x0|p-1+m2|x1|p-1+m3,m1,m2,m3为非负常数;
[H4]f(t,x,x′)关于 x 单调递减.
2 主要结论
定理1 假设条件[H1]~[H3]满足,则方程(1)至少有1个T-周期解;当p≥2且条件[H4]成立时,方程(1)的解是唯一存在的.
证明:记~f(t,x,x′)=f(t,x,x′)-e(t),设x是方程(φp(x′))′= λ~f(t,x,x′),λ ∈ (0,1)的解,即

令φp(x′)=y,方程(3)等价变形为如下方程组

式中φq(s)为φp(s)的反函数.设t是0x(t)的最大值点,即x(t0)=mtaRx x(t),显然x′(t0)
∈=0,又y(t0)= φp(x′(t0))=0,可证,y′(t0)≤0.假设y′(t0)>0,则由极限保号性知,∃σ >0,当t∈[t0,t0+ σ]时,y′(t)> 0,即y(t)> y(t0)=0,t∈[t0,t0+σ],又x′(t)= φq(y(t))> 0,得x(t)在[t0,t0+ σ]上单调递增,故 x(t)> x(t0)=0,t∈[t0,t0+σ],显然这与x(t)在t0取最大值矛盾,所以假设不成立,即y′(t0)≤0成立.
由方程(4)的第2个方程y′(t)的表达式,可知

即 f(t0,x(t0),0)≤ e(t0)≤|e|0,由假设[H1]可得

-d<x(t1)≤x(t)≤x(t0)<d
故(φp(x′))′= λf(t,x,x′)的解 x(t)有界,且
下证x′(t)也是有界的.,由方程(4)的第2个方程知



由引理2知,|y(t)|≤D2=D1em2T.
若0≤t≤t2,有0≤t2≤t+T≤2T,由y(t)的T-周期性及假设[H3]可得

由式(9)及0≤t≤t2,有|y(t)|=|y(t+T)|≤.即对于0 ≤t≤t2,有|y(t)|≤ D3=2D1em2T,由于 D2≤ D3,由式(8,9)可得,即‖x′‖∞≤,所以,即(φp(x′)′=的解 x(t)是有界的,i.e.,‖x‖ < M,取 Ω ={x∈ Χ:‖x‖ = ‖x‖∞+‖x′‖∞< M}.
显然方程(4)在∂Ω上无解,即引理1的条件(A1)满足.
对于x=±M∈R,x∈∂Ω且M >d,由假设[H3]有

即引理1的条件(A2)满足,由引理1的结论可知,方程(1)在Ω内存在一个解.
下证p≥2且假设[H4]满足时方程(1)的解还是唯一存在的.
设x1(t),x2(t)为方程(1)的两个周期解,且y1(t)= φp(x′1(t)),y2(t)= φp(x′2(t)),同时,
令u(t)=x1(t)-x2(t),v(t)=y1(t)-y2(t),由x′=φq(y)及方程(4)可得

下用反证法证明对于t∈[0,T],u(t)≤0成立.
证明:假设∃t0∈[0,T]使得u(t0)=max u(t)=x1(t0)-x2(t0)> 0,则
u′(t0)= φq(y1(t0))-φq(y2(t0))=0,即y1(t0)=y2(t0),且u″(t0)≤0,由于p≥2,q≤2,且定义当u=0,q=2时,|u|q-2=1;当u=0,q < 2时,|u|q-2=+∞.
由假设[H4]及y1(t0)=y2(t0)有
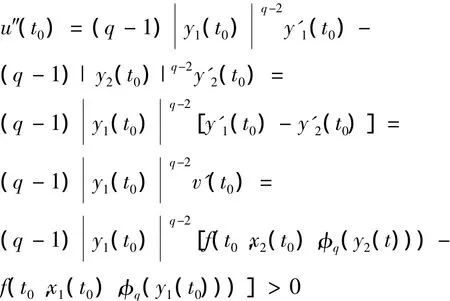
这与u″(t0)≤0矛盾,故u(t)≤0.
综上所证,方程(1)在p≥2及[H4]成立时,有且仅有一个周期解.定理1得证.
References)
[1] 郑亮,鲁世平,陈丽娟.一类二阶时滞微分系统的周期解和同宿解[J].扬州大学学报:自然科学版,2013,16(1):8-11,41.Zheng Liang,Lu Shiping,Cheng Lijuan.Periodic solutions and homoclinic solutions for a class of second order differential systems with delay[J].Journal of Yangzhou University:Natural Science Edition,2013,16(1):8-11,41.(in Chinese)
[2] 李志艳,葛渭高.三阶p-Laplace多点共振边值问题解的存在性[J].扬州大学学报:自然科学版,2012,15(3):12-15.Li Zhiyan,Ge Weigao.Existence of solutions for a thirdorder p-Laplace boundary value problem at resonance[J].Journal of Yangzhou University:Natural Science E-dition,2012,15(3):12-15.(in Chinese)
[3] 何涛,丁卫.二阶非自治系统的弹性周期解[J].江苏科技大学学报:自然科学版,2011,25(4):401-404.He Tao,Ding Wei.Periodic bouncing solutions for non-autonomous second order systems[J].Journal of Jiangsu University of Science and Technology:Natural Science E-dition,2011,25(4):401-404.(in Chinese)
[4] Yang Xiaojing,Kin Yongin,Lo Kueiming.Periodic solutions for a generalized p-Laplacian equation[J].Applied Mathematics Letter,2012(25):586-589.
[5] Wang Yong.Novel existence and uniqueness criteria for periodic solutions of a Duffing type p-Laplacian equation[J].Applied Mathematics Letter,2010(23):436-439.
[6] Lu Shiping,Ge Weigao.Some new results on the existence of periodic solutions to a kind of Rayleigh equation with a deviating argument[J].Nonlinear Analysis,2004,56:501-514.
[7] Manasevich R,Mauhin J.Periodic solutions for nonlinear systems with p-Laplacian-like operators[J].J Dfferential Equation,1998,145:367-393.
[8] Cheung Wingsum,Ren Jingli.Periodic solutions for p-Laplacian Rayleigh equations[J].Nonlinear Analysis,2004,59:107-120.
[9] Lu Shiping.Existence of periodic solutions to a p-Laplacian Lienard differential equations with a deviating argument[J].Nonlinear Analysis,2008,68(6):1453-1461.
[10] Ding Huisheng,Ye Guorong,Long Wei.Existence and uniqueness of periodic solutions for a class of nonlinear equations with p-Laplacian-like operators[J].Advance in Differential Equations,2010,doi:10.1155/2010/197263.

