基于批量分割的虚拟单元制造系统多阶段动态调度

吕 洁，王 洁

(江苏科技大学经济管理学院，江苏镇江212003)

虚拟单元制造系统(virtual cell manufacturing system，VCMS)［1］是单元制造模式的新发展，是近年来发达国家得到日益重视的一种先进制造方式.批量分割是虚拟单元管理活动中必须考虑的关键元素，是指将大的生产批量分割为小的子批量，使得同一产品的各工序在连续的加工中心上产生重叠(横向分割)，从而加快产品加工的进程，减少完工时间和在制品库存.它已经广泛用于减少流水车间和作业车间的完工时间.目前国内外已经存在一些关于批量分割的研究，文献［2］中研究了混流生产条件下批量和提前期联合确定问题，但仍缺乏对于虚拟单元下的批量分割的研究，而且关于大型复杂单件型企业的虚拟单元内设备“一专多能”且同类设备有多台这一问题所引起的批量分割研究不多.因此，文中针对虚拟单元下批量分割的特点研究设备“一专多能”及存在相同设备的批量分割调度问题.文献［3-4］中研究了考虑批量分割的单元制造系统设计问题.还有一些学者对批量分割下的生产计划［5］、成组布局设计［6］以及多目标优化［7-8］进行了研究，文献［9］和［10］中分别强调了VC 下批量分割的重要性和转移批量的效果.另外，对于解决批量分割的启发式算法需要进一步改进.一些文献提出的算法可以解决调度问题［11-12］，但是部分存在计算时间过长，不利于解决大规模问题等缺陷.

由于多数研究都假设虚拟单元调度过程中不允许批量分割，因为批量分割的加入在很大程度上增加了调度的难度，而带批量分割的调度问题在实际的虚拟单元调度过程中普遍存在.因此，为了解决这一问题，文中将一阶段扩展为多阶段，提出了一个多阶段虚拟单元动态调度数学模型，来解决虚拟单元批量分割调度问题，并体现出批量分割带来的降低成本的特点.所讨论的批量分割还包含在具有同种功能的机器上同时进行分割(纵向分割)，考虑运输距离并确定设备上的批量种类、大小和顺序，最终达到总生产成本最小化的目标，其中总生产成本包括库存成本、运输成本和加工成本.

1 批量分割多阶段动态调度模型

1.1 问题描述

模型中包含多个阶段，多种类型的零件，多种类型设备，同种类型的设备可能不止一台，设备的最大生产能力已知，并且在整个计划期内是不变的.每种类型的零件都有多条工艺路线进行选择，设备在物理位置上是不移动的，并且机器间的距离是已知的.该模型考虑了虚拟单元设备负荷的均衡，资源利用情况，调整准备时间等因素来决定设备批量大小.模型中共包含 U 个工作区(u=1，2，3，…，U)，将一个计划期分为P个阶段(p=1，2，3，…，P)，可能存在 b个子批(b=1，2，3，…，B).

1.2 目标函数

文中针对生产车间的需要，将最小生产成本作为最终目标，其中包含运输成本、库存成本和加工成本.

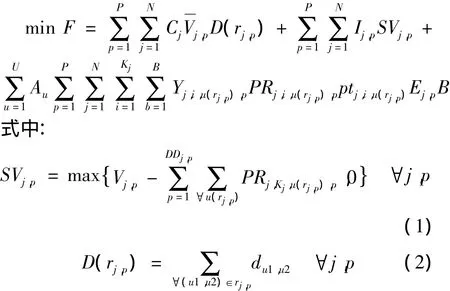
式(1)为各阶段作业j的库存量;式(2)为生产路线的运输距离的计算公式;N为作业j的总数量;Cj为单位距离单位作业j的移动成本;Vj，p为p阶段作业j的客户需求量;D(rj，p)为加工路线 rj，p的总距离;Ij，p为p阶段作业j的库存成本;Au为单位时间工作区u的加工成本;Kj为作业 j的总工序数量;Yj，i，u(rj，p)，p=1表示如果p阶段在u工作区rj，p路线下作业j的加工工序 i已经在加工，否则为 0.PRj，i，u(rj，p)，p表示 p 阶段在u工作区rj，p路线下作业j的加工工序i的加工率;ptj，i，u(rj，p)为在工作区 u(rj，p)生产一个单位作业 j的工序i的加工时间;Ej，p为p阶段作业j的子批量大小;DDj，p为 p 阶段作业 j的截止日期;u(rj，p)为 p 阶段作业j的加工路线所使用的工作区u;du1，u2为两个工作区之间的距离.

1.3 约束条件

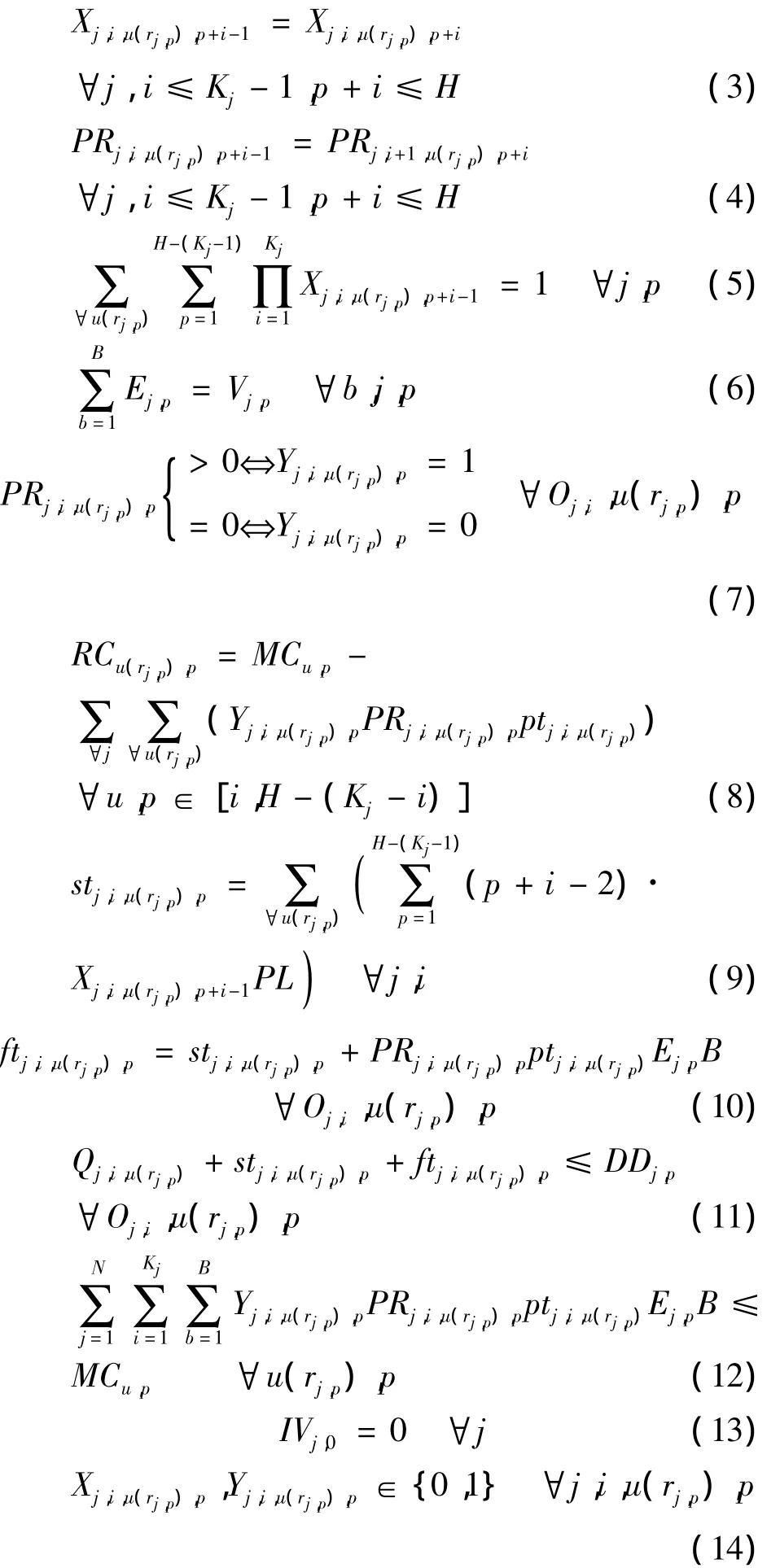
约束(3)表示当作业j的工序i完成之后，作业j的工序i+1立即开始加工;约束(4)表示同一作业的后一个工序的加工率等于前一个工序的加工率;约束(5)表示所有作业的开始时间都在计划期内;约束(6)表示保证批量分割后作业的所有子程序的批量大小和等于该作业最初的批量大小;约束(7)表示加工率大于等于0;约束(8)表示p阶段工作区u的剩余能力;约束(9)和(10)表示加工的开始时间和结束时间;约束(11)表示所有作业都要在交货截止日期前完成;约束(12)表示所有作业被分配到到设备上可以按时完成;约束(13)表示在计划期初任何作业没有库存;约束(14)表示模型中各变量都是二进制的.

式中:PL为一个阶段的长度;H为计划期;rj，p为p 阶段工作 j的加工路线;Oj，i为作业 j的工序 i;MCu，p为p阶段工作区u的最大生产能力;D(rj，p)为加工路线 rj，p的总距离;Qj，i，u(rj，p)，b为工作区 u(rj，p)生产单位作业j的工序i的第b个子批的调整时间;RCu(rj，p)，p表 示 p 阶 段 工 作 区 u 的 剩 余 能 力;stj，i，u(rj，p)，p，b表示 p 阶段在 u 工作区 rj，p路线下作业 j的加工工序 i的第 b 子批的开始时间;ftj，i，u(rj，p)，p表示p阶段在u工作区rj，p路线下作业j的加工工序i的结束时间;Xj，i，u(rj，p)，p=1 表示如果 p 阶段在 u 工作区rj，p路线下作业j的加工工序i开始加工.否则为0.

2 混合优化算法

2.1 约束规划

约束规划是解决约束满足问题的有效方法.约束满足问题通常包含多个变量和变量值域.它的基本操作是一次挑选一个变量，并且在其值域中选出一个值，确保其与目前已有的解相兼容.如果这个解不满足约束则用新的解来替代它，如果没有可以使用的不违反任何约束的解，那就回溯到最近的已有变量，不断重复直至所有可行解都找到或所有可能的结合都考虑过.

2.2 离散粒子群算法

粒子群优化算法基本思想是通过共享种群内个体之间的信息对最优解或近似最优解进行定位［13］.种群指搜索空间内一组粒子，每个粒子代表一个可行解，穿梭于超空间内，并且有对自己最佳位置和对全局及临近解最佳位置记忆的能力.种群内的粒子相互交换信息并按下面的公式调整自己最佳的位置和速度.

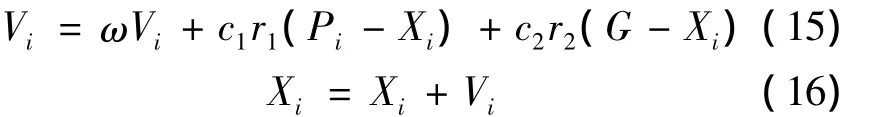
式中:Xi表示粒子i的位置，Vi表示粒子的速度，Pi是i之前访问过的最佳位置.G是全局的最佳位置，ω是控制之前速度对当前情况影响的惯性权重，通常随着搜索区域的减小而动态降低.

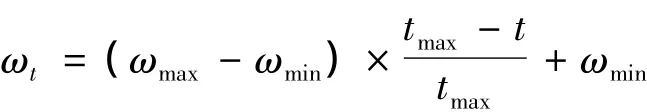
式中:ωmax和ωmin分别为惯性权重的最大值和最小值，tmax为最大重复次数.

在现实情况中，许多优化问题例如生产调度问题的空间集是离散的或性质上分散的.为了满足这一要求，便提出了离散粒子群优化算法.首先种群是由二进制变量构成的.其次，速度转变为概率变化，表示变量取值为1的机会.这一转化通过以下公式完成:s(Vi)表示相应位取值为1的可能性.

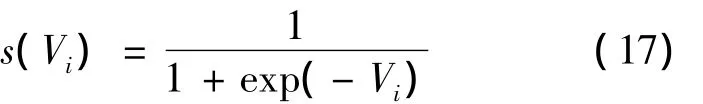
2.3 混合算法

1)初始化

初始化粒子规模为K，最大重复次数tmax;随机初始化各个粒子的位置，和速度;评价每个粒子的目标值，初始化和

2)过程反复

while(t≤tmax)

for k=1 to K

更新粒子k的速度

for p=1 to P

更新p阶段粒子k的调度顺序

while p阶段的生产调度不为空

在生产顺序中挑选第一个工作j

更新工作j所在工作区的任务

Check一致性

while(不一致)

检测关键设备并添加到冲突集

if关键设备有可替代资源

换一项新任务

Check一致性

else随机分配一个合适的机器

设置一致性

endwhile

计算p阶段工作j的产出及数量大小

从生产调度中检测该工作

endwhile

endfor

endfor

重复计数t=t+1

endwhile

3)从种群中找出目标值最好的解和相应的目标值

如果一项工作不能在截止日期前完成，或在用完上一阶段的额外能力后还是不能满足需求，那么会按不一致处理，并且检测出关键机器重新分配任务，约束规划在此处是单层回溯.当出现不一致时，该算法会检测出关键资源并检查该资源是否有替代资源.如果有，将会分配替代资源的单元来完成该工序.否则该算法不回溯，且在不考虑一致性的情况下用离散粒子群算法随机分配一个合适的工作区，接着调度下一工作，直至所有的工作都完成.

3 案例

3.1 问题及参数

为验证模型的有效性及算法的优越性，文中以中国内地某船厂舾装作业为例进行研究.文中选取了该工厂10个比较典型的管子加工作业和6类典型的工作区为例来进行应用分析，验证文中建立的模型效果.工作区信息如表1，各工艺的加工工艺信息如表2，表3描述的是各机器间的运输距离.

混合算法中用到的参数值如下:粒子规模为100;循环最大次数为100;最大惯性权重为0.8;最小惯性权重为0.2;c1和c2都等于2;粒子速度范围为［-4，4］;每周期包含32个阶段，每阶段时间是300min;每个作业需要3～5个工序;每周期生产作业的数量随机生成［50，80］.

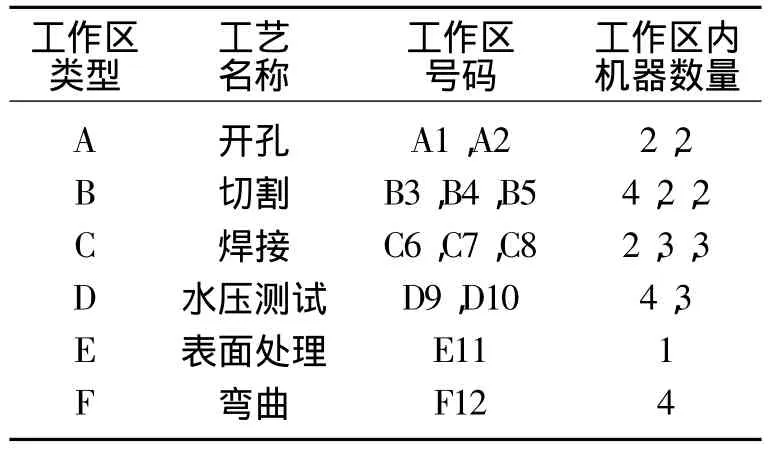
表1 工作区信息Table 1 Workspace information

表2 各作业的加工工艺信息Table 2 Processing information of jobs

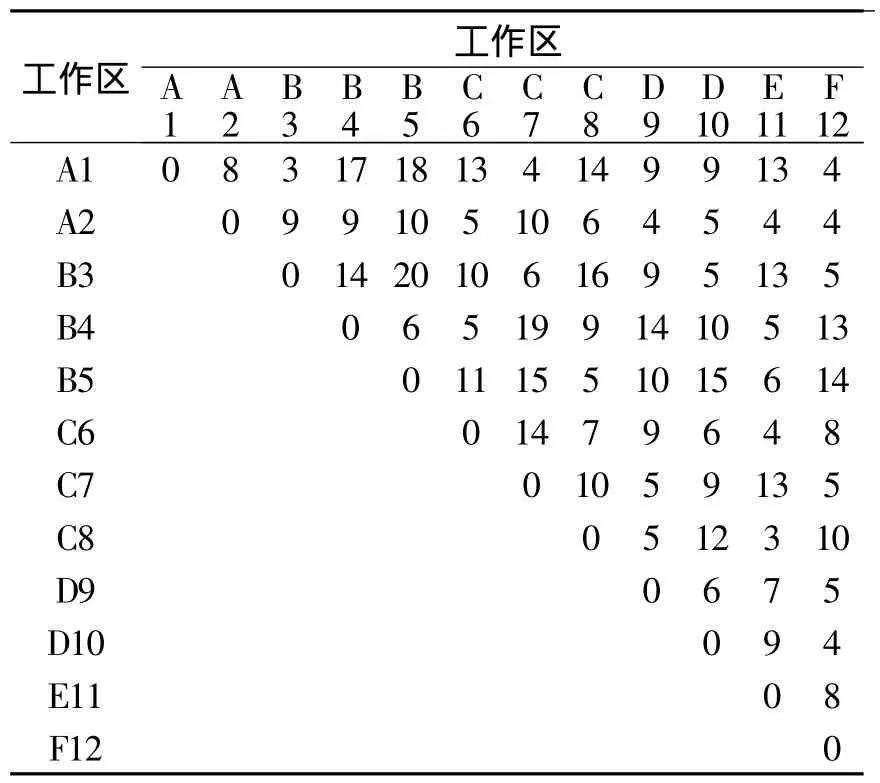
表3 工作区间的运输距离信息Table 3 Transport distance information of workspace m

表4给出了测试问题的方案.表中，(p，n，d，m)表示参数集.p为周期数，n为各周期作业数，d为截止日期，m为工作区数量.例如，方案1表示有5个周期，该周期的作业数在［5，10］中随机产生，截止日期在［αp，βp］中随机产生，其中 α =0.4，β =0.7，工作区为12个.

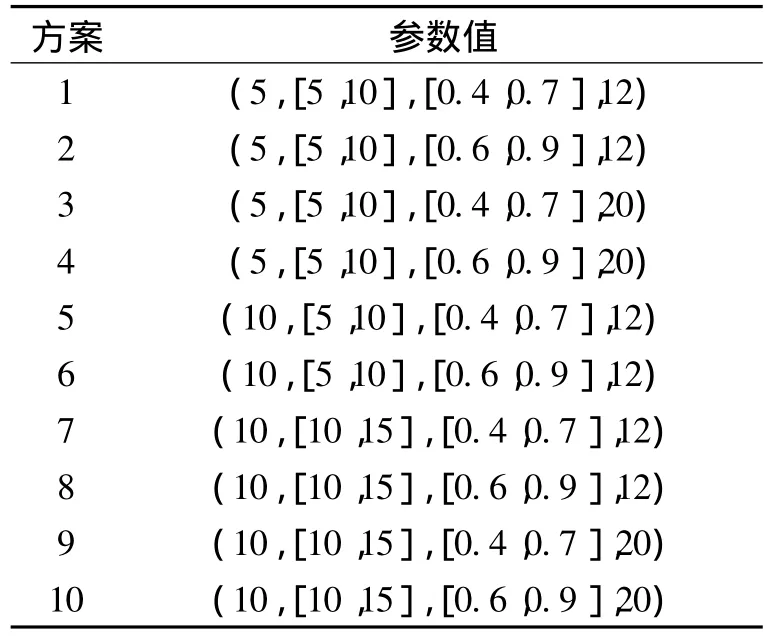
表4 方案参数列表Table 4 List of scheme parameter

每个方案随机产生5个问题，每个问题运行5次，从均值来比较混合算法和单独的离散粒子群算法的绩效.两种方法循环100次后，比较其成本差异和时间差异，计算方法如式(18)和(19).

3.2 批量调度结果及分析

文中使用混合算法在Matlab软件中对上述模型进行了计算.图1给出了10项作业的批量调度信息.然后，将混合算法和离散粒子群算法对表4中的10项方案进行测试，得到最终目标成本及计算时间的比较，体现了混合算法及批量模型的优越性.

从图1可以看出，一个周期被分为32个阶段，每个阶段的时间长度为300 min，系统的最大完工时间为150h，而10个作业均是在交货周期160h内完成，无作业延迟.在子批量调度的过程中一个子批量可能需要多个阶段来完成，但是在每个阶段都进行调度的检测，以满足设备的充分利用.其中作业5，7，8被分割为子批，在不同的加工路线下进行生产.作业5的加工批量为25，路线A1-B3-C7-F12-D10上的加工批量为17，路线A1-B3-C7-F12-D9上的加工批量为8.作业7加工批量为60，路线B3-C7-D9的加工批量为45，在同一工作区的另一设备上的加工批量为15.作业8加工批量为48，将其分为了两个相等的批量，路线A1-B3-C7-D9的加工批量为24，相同工作区的另一设备上的加工批量也为24.

图1 最终调度信息Fig.1 Final scheduling information

从此调度信息可以看出，在虚拟单元中进行批量分割可以缩短完工时间.在确定子批量的大小时要考虑设备的资源利用状况、调整时间和成本等因素，并且在调度的过程中需要不断的检验调度现状，在各个不同的阶段，对剩余资源进行重调度，从而提高设备的利用率.

表5为两种算法循环100次后的比较结果，与单纯的DPSO相比，混合算法能给出更好的解.对于相同的问题，混合算法所消耗的成本更少，但是所消耗的计算时间较长，因此进一步比较了在相同时间长度的情况下两种算法的绩效.比较结果如表6，其中Tops表示的是循环100次离散粒子群算法的计算时间.从调度结果可以看出，与单纯的离散粒子群算法相比，约束规划和离散粒子群算法的混合算法在求解模型时能给出更好的解.当问题的规模扩大时，或是截止日期更近时，这一混合算法的优越性更加明显.

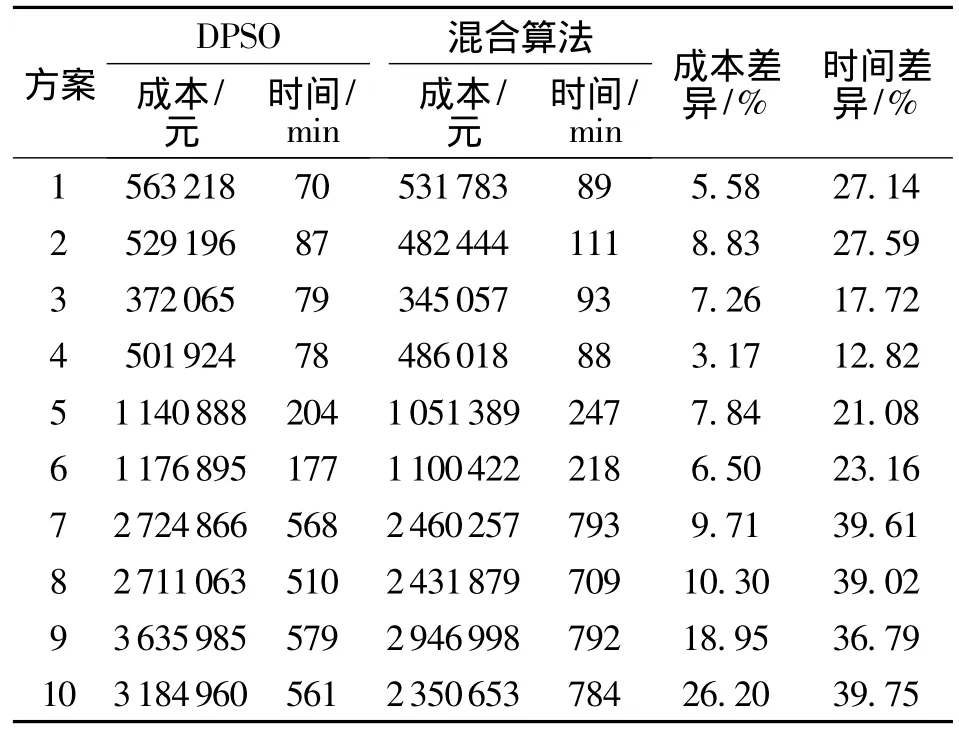
表5 离散粒子群算法与混合算法计算结果比较Table 5 Comparison of DPSO and hybrid algorithm

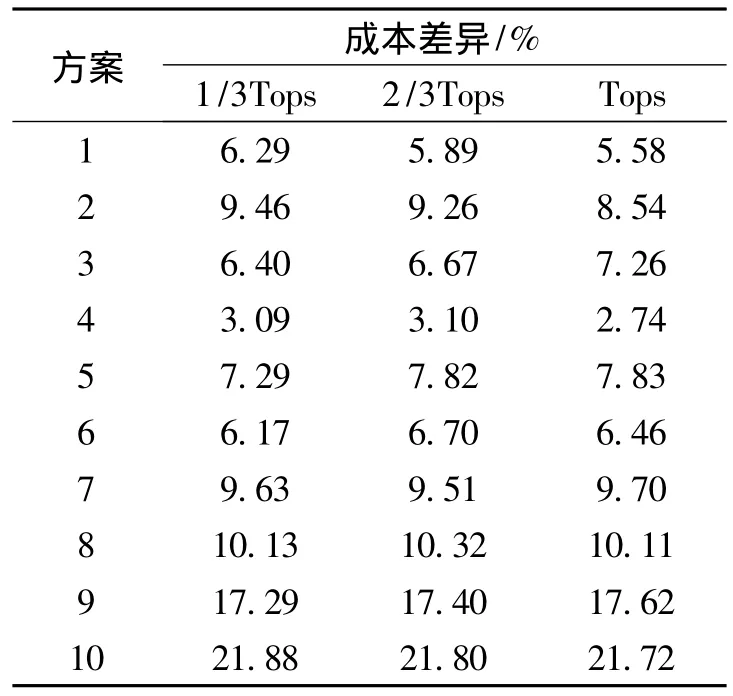
表6 两算法在相同计算时间下的成本差异Table 6 Cost difference of the two algorithms under thesame computing time

4 结论

文中主要讨论了制造系统内的设备“一专多能”，同类设备不止一台情况下的虚拟单元批量分割调度问题.由于批量分割调度的复杂性，文中构建了一个多阶段动态调度数学模型，根据当前系统的生产状态对作业进行排序，计算总生产成本，弥补了现有文献对虚拟单元内批量分割调度模型研究的不足.

案例研究结果表明，该调度模型能够在完工时间内完成作业调度，缩短了完工时间，并且通过对比体现了其成本优势.另外，由于虚拟单元下的批量调度更符合实际，说明在虚拟单元条件下讨论批量分割的调度问题是十分必要的.

在实际生产中，含有瓶颈的虚拟单元批量分割调度也可能发生，可以进一步研究相关启发式算法的优化，从而得到更好的调度模型.

References)

［1］ Mak K L，Lau J S K，Wang X X.A genetic scheduling methodology for virtual cellular manufacturing systems:an industrial application［J］.International Journal of Production Research，2005，43(12):2423 -2450.

［2］ 韩文民，叶涛锋.混流条件下基于TOC制定生产作业计划的关键问题:研究现状及发展探讨［J］.江苏科技大学学报:自然科学版，2005，19(6):92-96.Han Wenmin，Ye Taofeng.Critical problems on determining production scheduling for hybrid flow shop based on TOC:a survey［J］.Journal of Jiangsu University of Science and Technology:Natural Science Edition，2005，19(6):92-96.(in Chinese)

［3］ Lockwood W T，Mahmoodi F，Ruben R A，et al.Scheduling unbalanced cellular manufacturing systems with lot splitting［J］.International Journal of Production Research，2000，38:951 -965.

［4］ Defersha F M，Chen M.A comprehensive mathematical model for the design of cellular manufacturing systems［J］.International Journal of Production Economics，2006，103:767 -83.

［5］ Ahkioon S，Bulgak A A，Bektas T.Integrated cellular manufacturing systems design with production planning and dynamic system reconfiguration［J］.European Journal of Operational Research，2009，192:414 -428.

［6］ Kia R，Baboli A，Javadian N，et al.Solving a group layout design model of a dynamic cellular manufacturing system with alternative process routings，lot splitting and flexible reconfiguration by simulated annealing［J］.Computers and Operations Research，2012，39(11):2642 -2658.

［7］ 白俊杰，龚毅光，王宁生，等.多目标柔性作业车间分批优化调度［J］.计算机集成制造系统，2010，16(2):396-403.Bai Junjie，Gong Yiguang，Wang Ningsheng，et al.Multi-objective flexible job shop scheduling with lot-splitting［J］.Computer Integrated Manufacturing Systems，2010，16(2):396 -403.(in Chinese)

［8］ 曾强，杨育，沈玲，等.基于准时交货的批量生产 FJSP多目标优化［J］.计算机集成制造系统，2011，17(8):1780-1789.Zeng Qiang，Yang Yu，Shen Ling，et al.Multiobjective optimization for batch production FJSP based on just in time delivery［J］.Computer Integrated Manufacturing Systems，2011，17(8):1780 -1789.(in Chinese)

［9］ Kesen S E，Gungor Z.How important is the batch splitting activity in scheduling of virtual manufacturing cells［J］.International Journal of Production Research，2011，49(6):1645-1667.

［10］ Ye Taofeng.Analysis on multi-stage lot streaming:The effect of transfer［J］.Computers ＆ Industrial Engineering，2012，62:1046 -1054.

［11］ Defersha F M，Chen M.A hybrid genetic algorithm for flowshop lot streaming with setups andvariable sublots［J］.International Journal of Production Research，2010，48(6):1705-1726.

［12］ Pan Q K，Suganthan P N，Liang J J，et al.A local-best harmony search algorithm with dynamic sub-harmony memories for lot-streaming flow shop scheduling problem［J］.Expert Systems with Applications，2011，38:3252 -3259.

［13］ Kenndey J，Eberhart R C.Particle swarm optimization［J］.IEEE International Conference on Neural Network，1995:1942-1948.