实时路网单车多任务物流配送路径优化
彭 勇,何俊生
(重庆交通大学 交通运输学院,重庆 400074)
末端物流是货物送达消费者的物流活动。电子商务的繁荣带动诸如快递公司这样的末端物流企业业务的快速增长,末端物流效率越来越受到重视。
末端物流配送路径问题实际上是一类车辆路径问题[1]。对于末端物流配送路径问题,真实路网结构、车辆时变及多任务特性应该在路径计划中受到关注[2-10]。考虑划区运营的城市快递服务,每个划定区域的客户由一辆车送货,这就形成单车路径优化问题[3-5,10]。文献[10]讨论了一类时变无能力约束车辆路径优化问题,建立了以配送总耗时最短为优化目标的无能力约束车辆路径优化模型。但对问题求解使用的是枚举法,难以应用于大规模问题的求解。笔者考虑城市末端物流配送实际,在真实路网结构下,研究有一个配送中心及多个客户,且客户需求由一辆装载能力有限的车辆提供送货服务的,具有时变特性的单车多任务末端物流配送路径优化问题。
1 单车多任务物流配送路径模型
令dij表示节点i到节点j的直达距离。若从i到j无直达路径,则用dij= ∞ 表示。变量yij(Ti)表示Ti时刻车辆从节点i到节点j的行驶速度。当车辆到达节点i的时刻为Ti,则此时从节点i直达节点j所用时间为dij/yij(Ti);若从i到j无直达路径则所用时间用∞表示。


则,数学模型如下:
目标函数,最小化配送时间如式(1):
(1)
平衡条件,即在某次任务中车辆到达与离开某点次数相同,见式(2):

(2)
对每个节点的配送为一次且仅为一次,见式(3):

(3)
到达节点j的时刻与从节点i出发时刻的关系如式(4):
Tj=Ti+tij(Ti),ifXijr=1
(4)
确保配送回路通过配送中心,如式(5):
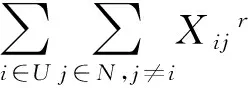
(5)
每条线路上的节点货物需求总量小于车辆的最大载运量,如式(6):

(6)
2 单车多任务物流配送路径模型Dijkstra-GA优化算法
VRP属于NP-Hard问题,解决此类问题多用启发式算法。由Holland教授提出的遗传算法(GA)具有较强的鲁棒性,广泛应用于VRP的寻优计算中。笔者将遗传算法与实时Dijkstra算法相结合(Dijkstra-GA)求解文中模型,遗传算法用于路径寻优,实时Dijkstra算法求解两点间路网时间最短路径[10]。
2.1 编 码
采用自然编码。如有6个客户,用1~6对其编号。首先将需要配送的客户随机排列,如[ 1,5,6,3,4,2,0 ],其中0为配送中心。假设最大允许配送路径数为4,即在形成的排列中随机插入2个节点0,假设变为[ 1,5,0,6,0,3,4,2,0 ],因为每个回路车辆最终要回到出发点,这里可在染色体两边添加0,形成染色体[ 0,1,5,0,6,0,3,4,2,0,0]。该染色体解码为车辆依次配送的3项任务:0→1→5→0; 0→6→0; 0→3→4→2→0。
2.2 适应值函数
以模型目标函数倒数作为适应值函数。
2.3 选择操作
取种群各个体适应值除以种群所有个体适应值之和,作为各个体选择概率;采用轮盘赌的方式选择个体。
2.4 交叉变异操作
以交叉概率Pc进行交叉操作,随机选取两个个体某段基因互换。对于互换后形成的新个体若有冲突基因(下划线表示), 新个体段的冲突基因对应交换,交叉操作结束。如:
个体1:[ 0 1 |3 4 0 6 5| 2 0 ]
个体2:[ 0 5 |3 2 6 0 4| 1 0 ]
↓↓
个体1′:[ 0 1 3 2 0 6 4 2 0 ]
个体2′:[ 0 5 3 4 6 0 5 1 0 ]
↓↓
个体1″:[ 0 1 3 5 0 6 4 2 0 ]
个体2″:[ 0 2 3 4 6 0 5 1 0 ]
以变异概率Pm进行变异操作,随机取个体两个基因位置互换,形成新个体。
2.5 终止条件
采用最大迭代次数为算法终止条件,算法流程见图1。

图1 算法流程Fig.1 The algorithm flowchart
3 算例分析
3.1 小规模运算分析
利用本文算法对文献[10]中的算例进行分析。设置初始群体规模为40,遗传迭代gen_max次数为100,交叉概率pc= 0.6,变异概率pm= 0.05,在CPU2.0 GHz,内存2 GB的计算机上连续进行10次运算。10次运算的最优结果皆为1 h 33 min,路径为6→ 4→7→3→11→12→6,与用枚举法求得的结果[10]相同。本文算法连续10次运算用时如图2。
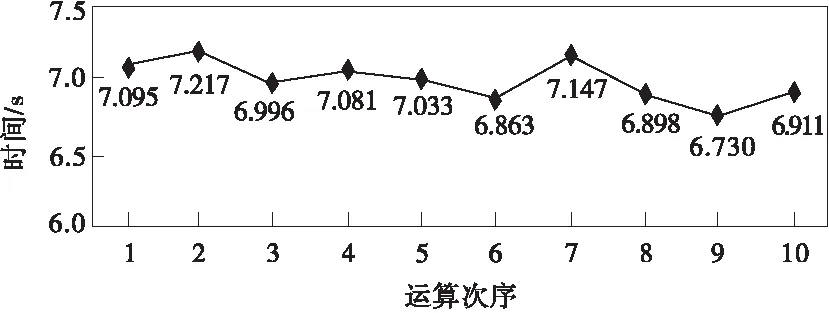
图2 连续10次运算用时Fig.2 Comparsion of consuming time of 10 consecutive computations
由图2可见,笔者提出的算法对于解决小规模运算问题可以给出满意的优化解,并且运算用时较短。
3.2 大规模运算分析
某市某片区路网中共有139个节点,配送中心与配送节点信息如表1,各配送点需求量如表2。

表1 路网部分节点坐标
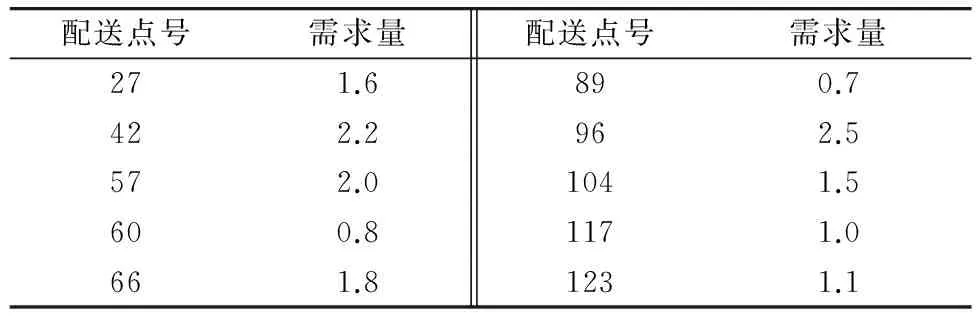
表2 各配送点需求量

图3 路网Fig.3 Road-net
假设车辆最大载运量取8,若不考虑路网时变性,每条路网上的行驶时间为常数,路段平均行驶速度为40 km/h,用文中算法求得的最短时间为1 h 44 min。其中1条配送虚拟路径如图4。图中实线表示第1次配送路径,虚线表示第2次配送路径。即从配送中心出发,按照图中3条回路标号依次完成配送。
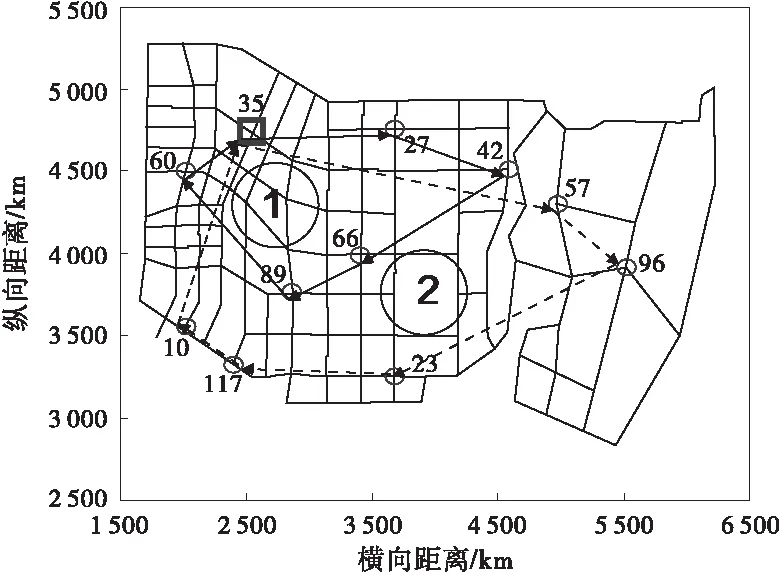
图4 不考虑时变路网其中1条配送虚拟路径Fig.4 One of distribution virtual paths when time-varying of road-net is ignored
若考虑路网时变特性,即考虑每天早高峰与晚高峰时段,某些路段的行车速度会因拥堵而减慢。为简化计算,设路段非高峰期车速均为40 km/h,某些路段高峰期(7:30—09:00,17:00—19:00)拥堵平均车速如图5。图中数字表示各路段平均车速,没有标注的路段为40 km/h。

图5 道路拥堵及平均速度Fig.5 Road congestion and average speed
采用遗传算法连续计算10次,求出的行驶最短时间都为1 h 50 min。其中1条配送虚拟路径如图6,图中实线表示第1次配送路径,虚线表示第2次配送路径。即从配送中心出发,按照图中两条回路标号依次完成配送。

图6 考虑时变路网其中1条配送虚拟路径Fig.6 One of distribution virtual paths when time-varying road-net is considered
10次运算中的一次种群最优适应值变化过程如图7。连续运行10次遗传算法,用时如图8。

图7 种群最优适应值变化过程Fig.7 The evolutionary process of the optimal value

图8 连续10次计算用时对比Fig.8 Comparsion of consuming time of 10 consecutive computations
从图8可以看出,利用遗传算法计算用时在79~80 s之间,计算时间是可以让人接受的,而图7也表明配送时间随算法寻优过程得到了很好的缩短。
若车辆按图4路径行驶,考虑高峰期拥堵对其影响,08:15发车,则配送完回到配送中心全程耗时3 h 12 min,比考虑路网时变特性优化路径配送多耗时1 h 22 min。
4 结 语
讨论了实时路网下末端物流配送问题,建立了基于实时路网的单车多任务路径优化模型。设计了Dijkstra-GA优化求解算法。通过对比研究及更大规模算例分析,验证了笔者所给出算法的有效性,并表明了考虑路网时变特性对末端物流配送路径计划的重要性。
[1] Dantzig G,Ramser J.The truck dispatching problem [J].Management Science,1959,6(1):80-91.
[2] Taillard E D,Laporte G,Gendreau M.Vehicle routing with multiple use of vehicles [J].Journal of the Operational Research Society,1996,47:1065-1070.
[3] 彭勇,谢禄江,刘松.时变单车路径问题建模及算法设计[J].重庆交通大学学报:自然科学版,2013,32(2):263-266.
Peng Yong,Xie Lujiang,Liu Song.Route modeling and algorithm designing of time-dependent single vehicle [J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(2):263-266.
[4] 彭勇.变需求车辆路线问题建模及基于Inver-over操作的PSO-DP算法[J].系统工程理论与实践,2008,28(10):76-81.
Peng Yong.Research on vehicle routing problem with stochastic demand and PSO-DP algorithm with Inver-over operator [J].Systems Engineering-Theory & Practice,2008,28(10):76-81.
[5] Gribkovskaia I,Laporte G,Aliaksandr S.The single vehicle routing problem with deliveries and selective pickups [J].Computers and Operations Research,2008,35(9):2908-2924.
[6] Malandraki C,Daskin M S.Time dependent vehicle routing problems:formulations,properties and heuristic algorithms [J].Transportation Science,1992,26(3):185-200.
[7] Kok A L,Hans E W,Schutten J M J.Vehicle routing under time- dependent travel times:the impact of congestion avoidance [J].Computers & Operations Research,2012,39(5):910-918.
[8] 王祥生,马寿峰.实时路况信息下配送路径的优化[J].工业工程,2008,11(1):113-116.
Wang Xiangsheng,Ma Shoufeng.Optimization of delivery routes based upon real-time traffic information [J].Industrial Engineering Journal,2008,11(1):113-116.
[9] 孙国华.基于真实路网的车辆路径问题研究[J].物流技术,2011,30 (1):43-45.
Sun Guohua.Solution to the real road network based vehicle routing problem [J].Logistics Technology,2011,30(1):43-45.
[10] 彭勇,刘洋.时变路网无能力约束车辆路径优化[J].价值工程,2012,31(9):114-116.
Peng Yong,Liu Yang.Uncapacitated vehicle route optimization based on time-dependent road network [J].Value Engineering,2012,31(9):114-116.

