引信安全系统的直线超声电机设计与试验研究

唐玉娟，王新杰，王炅

(南京理工大学 机械工程学院，江苏 南京210094)

0 引言

超声电机是20 世纪80年代以后逐渐发展起来的一种新型电机，它的基本工作原理是利用压电陶瓷的逆压电效应激发弹性体产生超声振动来实现电能向机械能的转换，并通过定、动子之间的摩擦界面完成动力输出［1-7］。超声电机具有许多独特的优点，在很多领域都得到了应用。德国PI 公司开发了基于直线型超声电机的半导体制造运动平台;日本佳能公司已有37 种照相机聚焦镜头应用了超声电机;美国在宇宙飞船、火星探测、运载火箭等航空航天工程中都应用了超声电机;周铁英等研制出了1 mm圆柱式超声电机并将其成功应用在OCT 内窥镜中［8］;南京航空航天大学精密驱动研究所将超声电机成功用于多关节机器人、核磁共振注射器和机翼颤振模型试验［9-10］。其中直线型超声电机具有功率/质量比大、直线运动推力可直接产生、响应快、位置分辨率高、断电自锁、结构简单、设计灵活、无电磁干扰等特点，特别适合于小型、精密直线运动装置的驱动和控制［11-12］。目前还未发现直线型超声电机在引信安全系统中应用的相关文献。基于以上优点，将直线型超声电机用在引信安全系统中是一种很好的选择。本文针对引信安全系统设计了一种直线超声电机。

1 电机结构及运行机理

1.1 电机结构

本文设计的面外模态双驱动足直线电机由动子和定子组成，定子和动子通过预压力紧密接触。定子下端面贴有两片压电陶瓷片，上端面凸出部分为两驱动足;动子下端面的中间凸起部分，起运动限位作用。动子和定子中各有一通孔，用作传火通道:通孔错开时，引信处于隔火状态;通孔对正时，为隔爆机构对正状态。电机初始状态如图1所示。

1.2 定子工作模态的选取

以驱动足所在的定子上表面为研究对象，选取定子一阶纵振模态E1和上表面的面外二阶弯振模态B2.

一阶纵振振型函数为

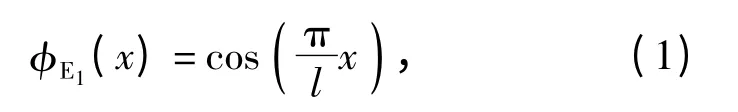
二阶弯振振型函数为

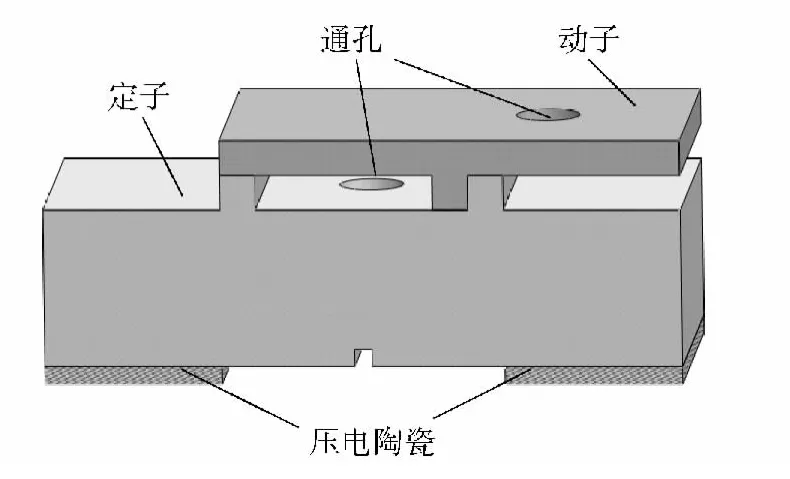
图1 电机初始状态Fig.1 Initial state of motor

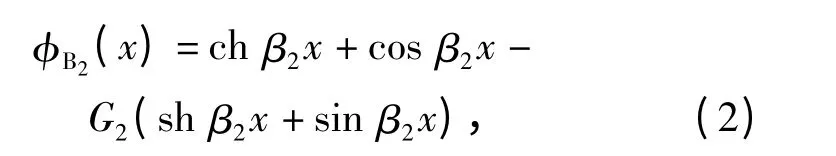
式中:G2、β2均为常量;l 为定子长度;x 为定子上任意点到原点O 的x 方向的距离。

其工作模态的振型图如图2所示，图中灰色部分为定子相应振型，黑色虚线为未变形前的定子轮廓。

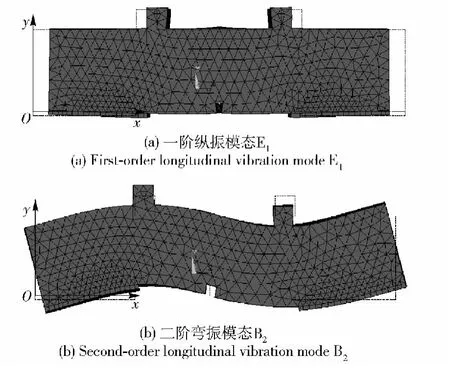
图2 定子工作模态振型Fig.2 The stator working modes

1.3 电机运动机理分析

电机定子结构如图3所示。电机的两驱动足分别位于弯曲振动的波峰、波谷处，定子的长度用L 表示，由自由-自由边界条件得到二阶弯振的波节位置分别为0.13L、0.5L 和0.87L［12］，因此波峰波谷位置分别为(0.13 L +0.5L)/2 和(0.87 L +0.5 L)/2处，即x =0.32L 和x =0.69L 处。采用两片压电陶瓷对电机定子进行激励，分别贴在定子底面两侧。两片压电陶瓷极化方向相反，分别施加电压信号sin(ωt+α)和sin(ωt+β)激励出定子两相振型。

一阶纵振使驱动足获得x 方向上的往复位移，二阶弯振使驱动足获得y 方向上的往复位移。由运动学可知:若一个质点以同一个频率在互相垂直的两个方向振动时，则质点的运动轨迹是一个椭圆。这样驱动足上的质点循环往复做椭圆运动，通过摩擦力带动动子运动。下面通过解析法验证电机驱动足的椭圆轨迹。

x 向伸缩振动和y 向弯曲振动响应函数分别为

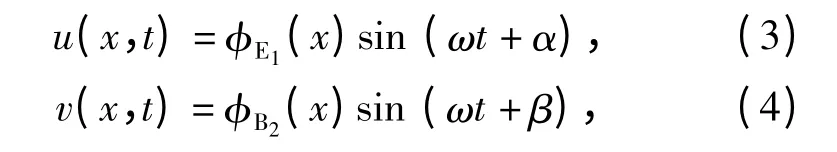
式中:ω 为振动角频率;t 为时间;α 为纵振初始频率;β 为弯振初始频率。由(3)式、(4)式中消去时间参数t 可得到［13］

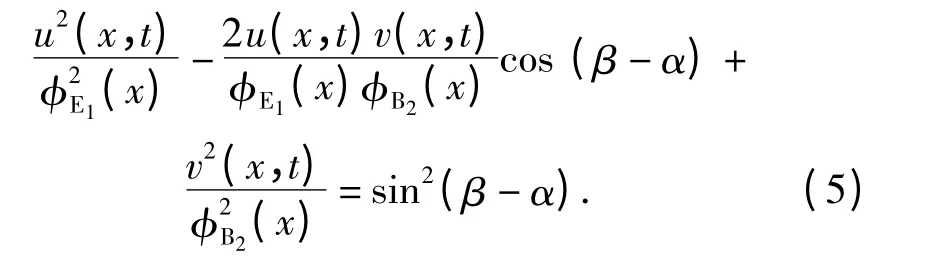
可以看出当β -α 为π/2 时，(5)式为标准椭圆方程:

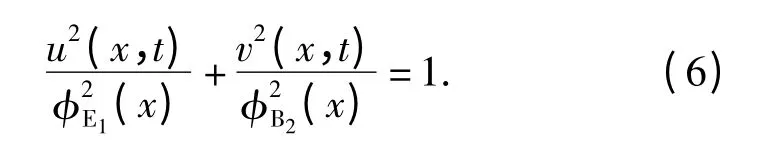
即当x 向伸缩振动响应和y 向弯曲振动响应的相位差为90°时，驱动足上每一点的运动轨迹为一椭圆，正是由于这些椭圆运动，电机定子才能推动动子产生直线运动。因此，实际工作中分别对两块压电陶瓷片施加cosωt 和sinωt 的电压信号，两片压电陶瓷片的极化方向相反。

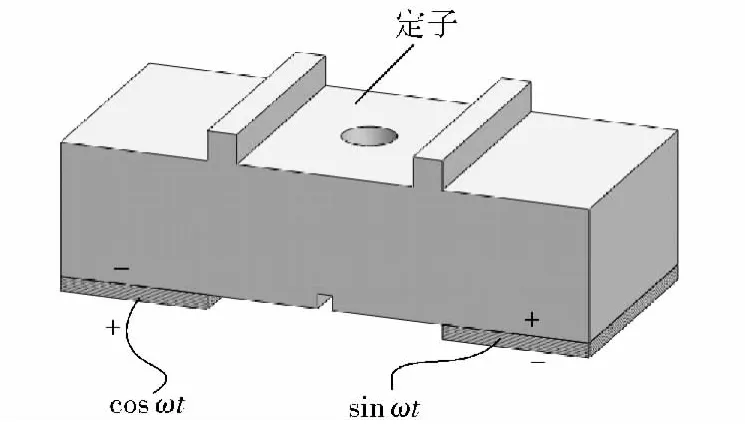
图3 电机定子结构Fig.3 Motor stator structure

2 电机仿真分析与参数确定

2.1 电机定子两相模态分析

电机工作所采用的一阶纵振和二阶弯振的频率必须一致，因此需要对定子的结构尺寸进行合理设计，研究每一个结构参数对两相频率变化的影响系数，即对结构参数进行灵敏度分析，找出对纵振频率和弯振频率灵敏度影响均较大的参数作为设计变量，对结构进行优化，最终使两相模态频率达到一致。图4为电机定子结构参数简图。

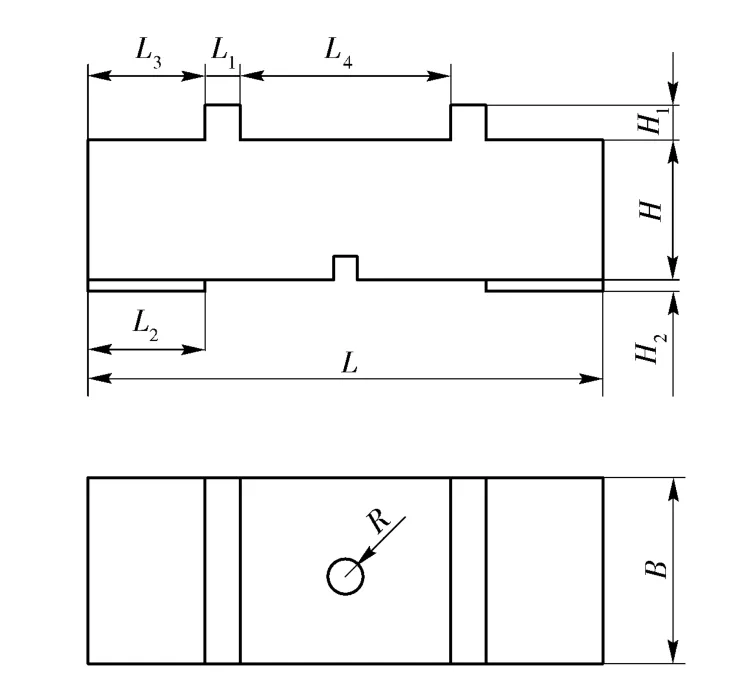
图4 电机定子结构参数简图Fig.4 Structure parameters of stator

结合引信安全系统的结构尺寸，定子长度L 取为18 mm，压电陶瓷的宽度L2=5 mm，厚度H2=0.2 mm，即这3 个参数为常量。考虑到电机在引信夹持装置中的定位，定子底部开一个0.5 mm×0.5 mm 通槽。由于2 个驱动足的中心位置分别在x =0.32 L 和x=0.69 L 处，因此L4可由L1表示，即L4=0.37L -L1;同理L3也可由L1表示，即L3=(0.63L -L1)/2.剩余L1、B、H、H1、R 5 个待确定的结构参数。

为了进行有限元分析，需要给出各待确定结构尺寸的初始值。将定子看作矩形板，为了使该矩形薄板两个振动模态频率尽可能相等，通常取L/H =4［14］. 则H 初值取为4.5 mm，其他待定参数初值如表1所示。

表1 各参数初始值Tab.1 The initial values of related parameters

利用有限元软件ANSYS 对定子初始结构进行模态分析，定子弹性体的材料为磷青铜，其密度为8 800 kg/m3，弹性模量为1.13 ×1011Pa，泊松比为0.33;压电陶瓷采用PZT8，其密度为7 600 kg/m3，机电耦合系数为0.53，机械品质因数为800，居里温度为300 ℃，介电损耗为0.5，压电常数为d31=95 pC/N，d33=245 pC/N，d15=190 pC/N，有限元分析时磷青铜和PZT8 分别选择SOLID45 单元和SOLID5单元。

由分析结果可得一阶纵振模态频率fE1=90 397 Hz，二阶弯振模态频率fB2=94 047 Hz，两相模态频率值相差较大为3 650 Hz，但是这两个振型是模态提取时紧邻的两阶振型，软件所提取的一阶纵振和二阶弯振是在一个频率范围内振幅最大的情况，在这个频率范围内有很多弱化的一阶纵振和二阶弯振，为各参数值的优化提供了可能性，只要合理设计各参数，两个振型频率会达到一致。

2.2 参数确定

针对两相模态频率一致性问题，首先将表1中的参数按顺序指定为灵敏度分析变量pi(i =1，2，…，5)，对5 个参数进行灵敏度分析。根据单一变量原则，即控制唯一变量而排除其他变量干扰从而分析唯一变量的作用，得到一阶纵振频率和二阶弯振频率随各参数变化的规律分别如图5和图6所示。

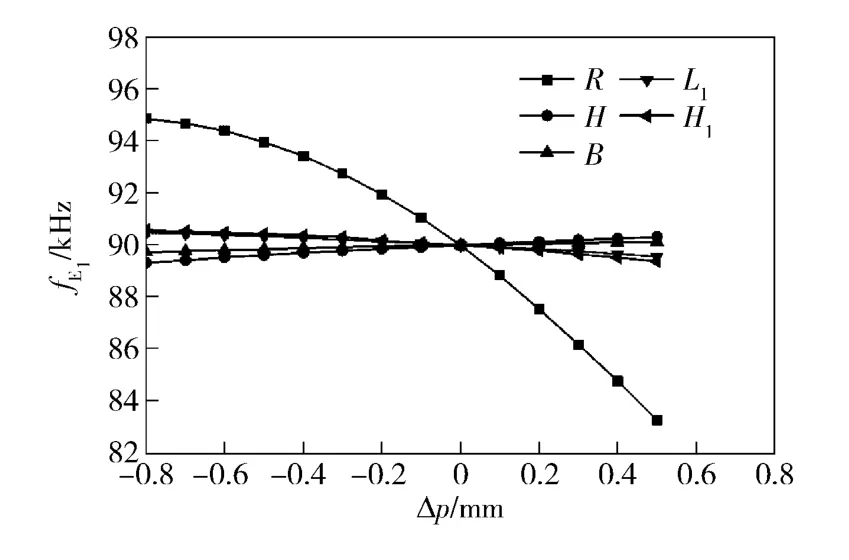
图5 一阶纵振频率fE1随各参数变化的规律Fig.5 The parameter-dependent curves of the first-order longitudinal vibration frequency fE1

由图5可以看出R、B、L1、H、H15 个待确定的结构参数中，B、L1、H、H1变化对一阶纵振频率fE1变化影响甚微，但是定子中的通孔半径R 的变化对fE1的变化影响十分明显，随着R 的增大，fE1显著下降，是因为随着通孔半径R 的增大，定子的刚度减小，模态频率下降。

由图6可以看出R、B、L1、H、H15 个待确定的结构参数中，B 、L1、H1变化对二阶弯振频率fB2变化影响甚微，定子中的通孔半径R 的变化同样对fB2的变化影响十分明显，fB2随着R 的增大而下降;同时定子厚度H 对二阶弯振频率影响较大，fB2随着H 的增大而增大。

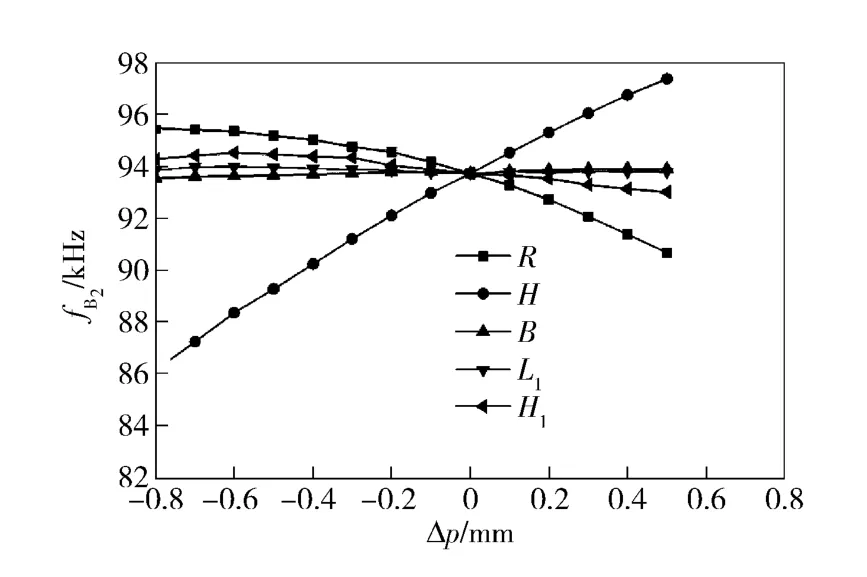
图6 二阶弯振频率fB2随各参数变化的规律Fig.6 The parameter-dependent curves of the second-order bending vibration frequency fB2

由此可见5 个待确定的结构参数中R 对两阶工作模态频率fE1与fB2的灵敏度较大，厚度H 对二阶弯振频率影响较大，其余参数灵敏度微小。

5 个待确定的结构参数对两阶工作模态频率fE1与fB2的一致性影响如图7所示。

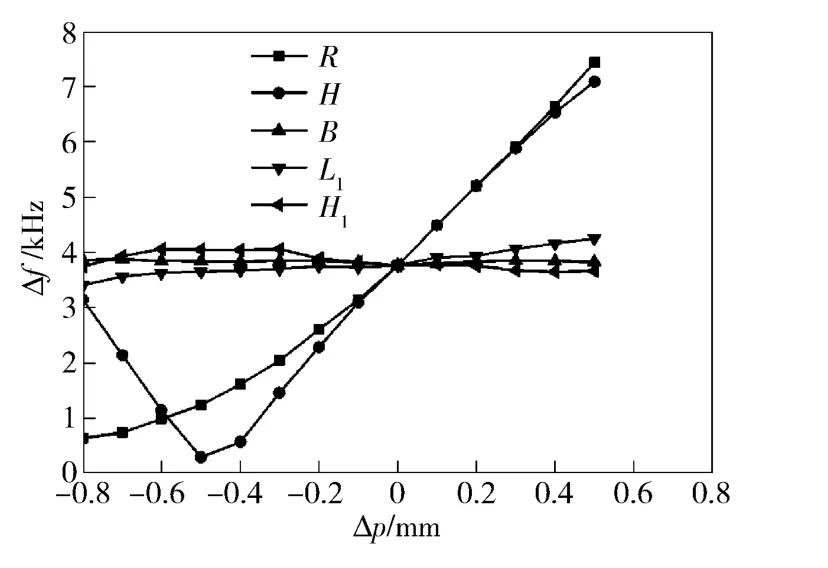
图7 各结构参数对两阶工作模态频率fE1与fB2的一致性影响Fig.7 Effect of structural parameters on the consistency of fE1 and fB2

由图7可以看出参数B、L1、H1的变化对频率一致性贡献甚微，参数R 的增量ΔpR对频率一致性影响较大，fE1与fB2的差值Δf 随着ΔpR的增大而增大。显然，定子上开孔不利于一阶纵振和二阶弯振频率一致，由于引信的特殊结构，定子上必须开孔作为传火通道，由以上分析可知R 越小越有利于两相频率一致;两相频率差Δf 随定子厚度H 的增大先减小后增大，在H=4 mm 时两相频率相差最小。

由以上分析，选取R、H 为最终设计参数，其余结构参数保持初始值不变。由图7可以得出随着R的减小，fE1与fB2不断接近，但是考虑到引信安全系统的实际情况，最小传火通道半径半径R 的值确定为1.7 mm;定子厚度取值为H =4 mm. 参数值确定后进行模态分析得到fE1与fB2的值分别为90 037 Hz、90 151 Hz，Δf =114 Hz，与初始参数情况比较如表2所示。可见尺寸优化对两阶频率一致性效果十分明显，两阶模态频率的差值由3 650 Hz 减小到114 Hz. 优化后的定子一阶纵振沿x 方向的位移等值线图和二阶弯振沿y 方向的位移等值线图如图8所示。

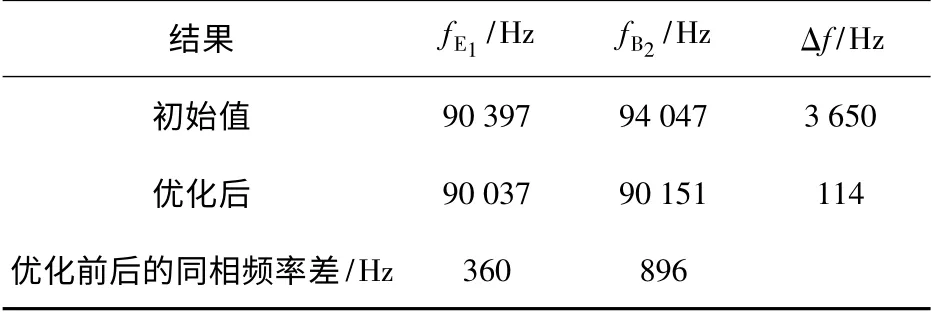
表2 参数优化前后两阶工作模态频率比较Tab.2 Modal frequency comparison before and after parameter optimization

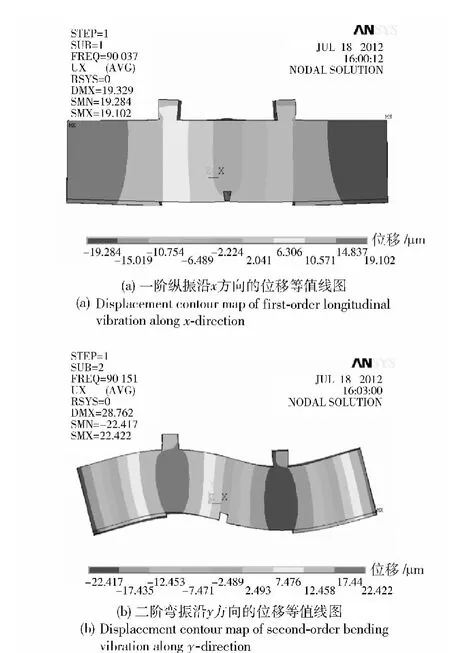
图8 参数优化后定子在工作模态下前视位移等值线图Fig.8 The working modal displacement contour maps of the optimized stator

3 实验验证与分析

图9为西安东方集团有限公司所加工制作的直线超声电机原理样机实物图。它由引信基座，电机和预压力结构组成。

图9 电机原理样机实物图Fig.9 Motor principle prototype

3.1 定子频率响应测试

应用PSV-300-B 型多普勒激光测振系统，对加工出来的电机定子进行了扫频测试，以确定电机实际的工作模态频率，图10 为扫频得到的定子频率响应曲线。

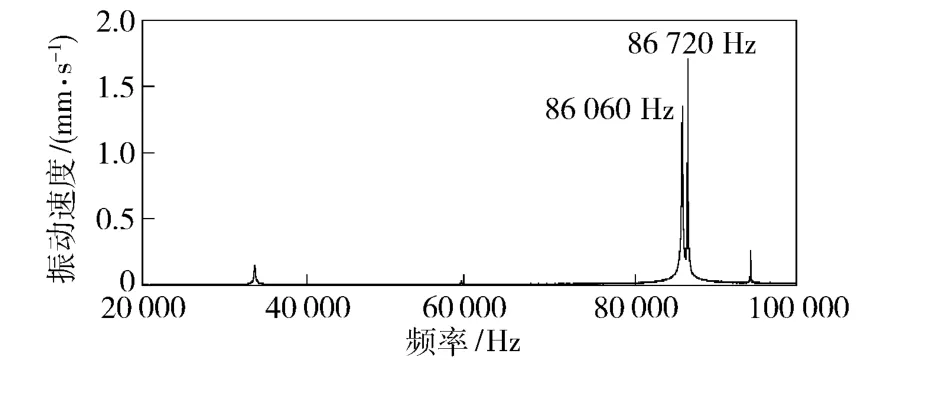
图10 定子频率响应曲线测试结果Fig.10 Test result of stator frequency response curve

扫频结果与优化结构有限元分析结果对比如表3所示。扫频得到的一阶纵振频率与二阶弯振相差660 Hz，可以满足设计要求。

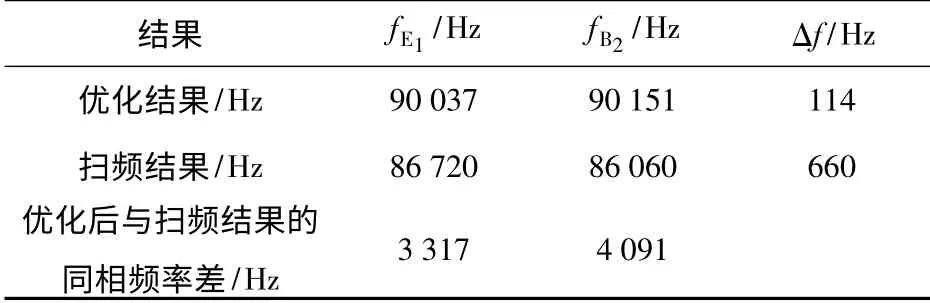
表3 扫频结果与优化结构有限元分析结果对比Tab.3 Comparison of frequency sweep results and finite element optimization results

测试结果与有限元分析结果有些差异，分析原因主要有以下三方面:1)利用有限元软件进行计算时，整个定子作为整体结构，但实际结构中，压电陶瓷元件和金属弹性体是通过粘胶材料黏结在一起的;2)存在材料和加工方面的误差，两片压电陶瓷安装的对称性也会对测试结果有影响;3)实际条件下电机的边界条件情况复杂，并不是有限元分析时理想的自由边界条件。

3.2 定子振动模态测试

根据激光多普勒测振仪扫频得到的电机实际的工作模态频率，对定子施加频率为86 060 Hz，峰峰值为40 V，电流为0.05 A 的正弦驱动电压，利用激光测振仪测得振型如图11 所示。可以看到两驱动足表面颜色不同，即代表两驱动足振动方向相反。从而说明在该驱动电压下定子的振型为二阶弯振，两驱动足分别在二阶弯振的波峰波谷处。并由此测得驱动足上的弯振幅值达到400 nm.

图11 定子二阶弯振振型Fig.11 Second-order bending vibration mode shape of stator

对定子施加频率为86 720 Hz，峰峰值为40 V，电流为0.05 A 的正弦驱动电压，并将定子立起来，利用激光测振仪测得振型如图12. 试验中可以观察到定子端面颜色交替变化，代表定子不停伸缩振动，说明在该驱动信号电压下定子的振型为一阶纵振。由此测得定子的纵振幅值达到500 nm.

图12 定子一阶纵振振型Fig.12 First-order longitudinal vibration mode shape of stator

3.3 电机运行性能测试

3.3.1 电机速度测试

在电机运动性能测试平台(如图13 所示)上，采用KEYENCE 激光位移传感器对电机运行特性进行测试，功率放大器输出两路同频相位差为90°的正弦信号，通过调节频率和驱动电压可得到不同驱动信号下电机的多次往返位移响应。

图13 电机运动性能测试平台Fig.13 Performance testing platform for motor

电机运动速度与驱动频率、驱动电压之间的关系拟合后如图14 所示。可见驱动频率对电机性能影响较大，最优工作频率86 540 Hz 在扫频得到的电机纵、弯模态频率范围之间，同时可得到驱动电压越高，电机运动速度越快。

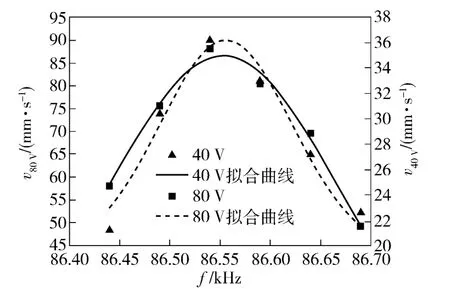
图14 电机速度与驱动频率的关系Fig.14 Motor speed versus driving frequency with different voltage

图15(a)显示的是在有预压力情况下，施加正弦电压峰峰值为80 V(引信中电源电压为9 V，经过驱动电路的升压最终加在电机上的电压为80 V)，频率为86 540 Hz 时电机往返15 次的位移响应，可见电机运行平稳。为便于观察，将电机往返1 次的位移响应情况放大，如图15(b)所示，图中曲线上升段表示电机由一端运动到另一端过程，曲线平台部分表示电机停止运动，曲线下降段表示电机返回初始位置过程。通过对测试结果进行数据处理得到:电机最大速度为88.2 mm/s;单程响应时间为0.057 s;单程最大位移为5 mm，与设计尺寸相符。

3.3.2 电机输出力测试

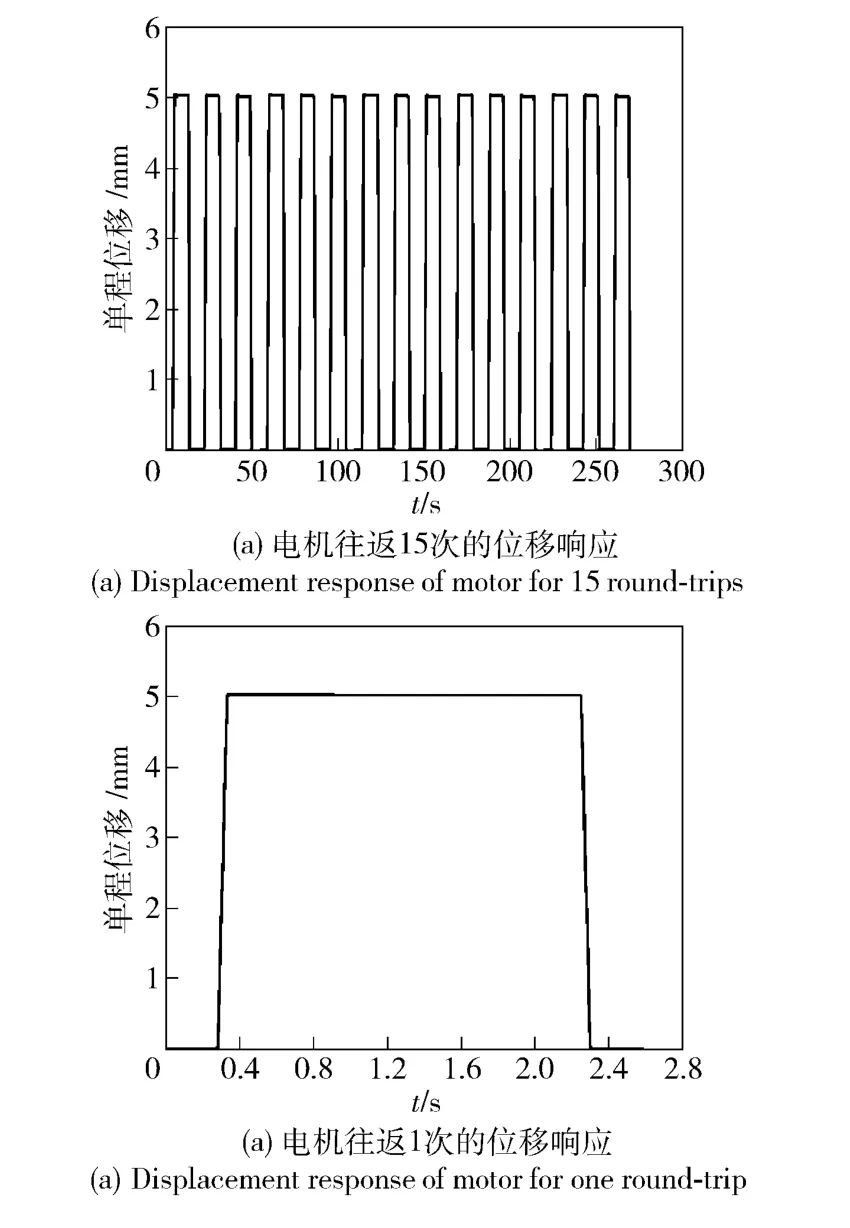
图15 电机运动位置与时间关系Fig.15 Motor displacement versus time

在电机动子一端固连一柔性弹簧，弹簧另一端固连在引信基体上，初始状态时，弹簧处于原长。电机运动时，动子压缩弹簧产生变形，采用KEYENCE激光位移传感器测量弹簧压缩变形量，如图16 所示，为了观察具体的内部测试结构，无预压力装置的电机如图中放大部分所示，实际测试中包括预压力装置。由弹簧刚度和压缩变形量可计算得到电机在最优工作频率86 540 Hz，施加信号电压峰峰值为80 V条件下最大输出力为2.3 N.

图16 输出力测试平台Fig.16 Output force testing platform for motor

4 结论

针对引信安全系统设计了一种直线型超声电机。根据引信安全系统的结构要求给出电机初始结构尺寸，利用有限元软件对电机定子进行了参数化建模，分析了各结构参数对电机两相模态频率一致性灵敏度;以电机两相模态频率达尽可能一致为优化目标，对电机结构尺寸进行了优化，并依照优化结果加工制作了电机样机。通过对定子进行了扫频测试和振动模态测试，得到了电机的两相工作模态，且两相频率接近，验证优化结果的正确性。在Upp=80 V，f=86 540 Hz 的两相相位差为90°的正弦信号激励下，电机的速度为88.2 mm/s，动子行程为5 mm 时所需时间为0.057 s，即为隔爆机构对正时间;电机输出力为2.3 N，动子为电机的组成部分，同时也是电机的负载，试验中观察到动子正反向灵活运动，即电机在驱动负载灵活运动的情况下净输出力为2.3 N，因此电机满足设计的功能要求。将直线型超声电机应用在引信安全系统中，为传统引信设计引入了新的思想，具有一定的工程意义和价值。

该直线型超声电机应用在引信安全系统中，必须要满足引信特殊的环境要求，例如电机能否抵抗常规弹药中的高过载问题，这是下一步重点研究的内容。

References)

［1］李玉宝，时运来，赵淳生，等.高速大推力直线型超声电机的设计与实验研究［J］.中国电机工程学报，2008，28(33):49 -53.LI Yu-bao，SHI Yun-lai，ZHAO Chun-sheng，et al. Research on linear ultrasonic motor with high speed and large thrust force［J］.Proceedings of the Chinese Society for Electrical Engineering，2008，28(33):49 -53. (in Chinese)

［2］Roh Y，Kwon J. Development of a new standing wave type ultrasonic linear motor［J］. Sensors and Actuators and Actuators A:Physical，2004，112(2):196 -202.

［3］金家楣，泮振锋，钱富.阶梯圆柱形压电振子直线型超声电机［J］. 振动、测试与诊断，2011，31(6):715 -719.JIN Jia-mei，PAN Zhen-feng，QIAN Fu. Linear ultrasonic motor using notched cylindrical piezoelectric vibrator［J］. Journal of Vibration，Measurement ＆ Diagnosis，2011，31(6):715 -719. (in Chinese)

［4］时运来，李珊珊，赵淳生. 轮式直线型超声电机定子的动态设计和分析［J］. 振动、测试与诊断，2011，31(1):1 -5.SHI Yun-lai，LI Shan-shan，ZHAO Chun-sheng. Dynamic design and analysis of wheel-shaped linear ultrasonic motor［J］. Journal of Vibration，Measurement＆Diagnosis，2011，31(1):1 -5. (in Chinese)

［5］Lu C Y，Xie T，Zhou T Y，et al. Study of a new type linear ultrasonic motor with double-driving feet［J］. Ultrasonics，2006，44:e585 -e589.

［6］姚志远，杨东，赵淳生.杆结构直线超声电机的结构设计和功率流分析［J］.中国电机工程学报，2009，29(24):56 -60.YAO Zhi-yuan，YANG Dong，ZHAO Chun-sheng. Structure design and power flow analysis of bar-structure linear ultrasonic motors［J］. Proceedings of the Chinese Society for Electrical Engineering，2009，29(24):56 -60. (in Chinese)

［7］石胜君，陈维山，刘军考，等.大推力推挽纵振弯纵复合直线超声电机［J］.中国电机工程学报，2010，30(9):55 -61.SHI Sheng-jun，CHEN Wei-shan，LIU Jun-kao，et al. A high power ultrasonic linear motor using push-pull longitudinal and bending multimode transducer［J］. Proceedings of the Chinese Society for Electrical Engineering，2010，30(9):55 -61. (in Chinese)

［8］周铁英，张凯，陈宇，等. 1 mm 圆柱式超声电机的研制及在OCT 内窥镜中的应用［J］.科学通报，2005，50(7):713 -716.ZHOU Tie-ying，ZHANG Kai，CHEN Yu，et al. Development of 1 mm cylindrical ultrasonic motor and application to OCT endoscope［J］. Chinese Science Bulletin，2005，50(7):713 -716.(in Chinese)

［9］邢仁涛，孙志峻，黄卫清，等.应用超声电机的多关节机器人的设计与分析［J］. 振动、测试与诊断，2005，25(3):179 -181.XING Ren-tao，SUN Zhi-jun，HUANG Wei-qing，et al. Design and analysis of multiple joint robotic arm powered by ultrasonic motors［J］. Journal of Vibration，Measurement ＆ Diagnosis，2005，25(3):179 -181. (in Chinese)

［10］赵淳生.超声电机技术与应用［M］.北京:科学出版社，2007.ZHAO Chun-sheng. Ultrasonic motors technologies and application［M］.Beijing:Science Press，2007. (in Chinese)

［11］许海，赵淳生.直线超声电机的发展及应用［J］. 中国机械工程，2003，14(8):715 -717.XU Hai，ZHAO Chun-sheng. Development and application of linear ultrasonic motors［J］. China Mechanical Engineering，2003，14(8):715 -717. (in Chinese)

［12］陈维山，赵学涛，刘军考，等.压电超声波马达发展现状及研究方向［J］. 电机与控制学报，2006，10(5):498 -502.CHEN Wei-shan，ZHAO Xue-tao，LIU Jun-kao，et al. A survey and current research of ultrasonic motor［J］. Electric Machines and Control，2006，10(5):498 -502. (in Chinese)

［13］陈永校，郭吉丰.超声波电动机［M］.杭州:浙江大学出版社，1994.CHEN Yong-xiao，GUO Ji-feng. Ultrasonic motors［M］. Hangzhou:Zhejiang University Press，1994. (in Chinese)

［14］刘剑，赵淳生.基于矩形薄板面内振动的直线型超声电机的研究［J］.声学学报，2003，28(1):86 -90.LIU Jian，ZHAO Chun-sheng. Study on the linear ultrasonic motor based on the vibration in plane of the rectangular plate［J］.Acta Acustica，2003，28(1):86 -90. (in Chinese)