大尺寸箭弹质量特性测量过程中位姿标定方法研究
王超,张晓琳,唐文彦,王军,马强
(哈尔滨工业大学 电气工程及自动化学院,黑龙江哈尔滨150001)
0 引言
质量特性参数是飞行体的一组重要参数,它包括质量、质心、转动惯量和惯性积。飞行器在使用之前都需要进行质量特性参数的测量,在工作时则根据这些参数来进行调整和控制,以达到姿态稳定并能够按照指定的轨迹飞行。
目前质量质心多采用多点支撑法测量,转动惯量和惯性积用扭摆法来测量,由于转动惯量和惯性积共有6 个独立分量,所以还需要在测量过程中变换产品的位姿。因此提高质量特性测量精度主要从3 个方面考虑:1)对测量质量质心所用到的称重传感器进行标定[1];2)对计算转动惯量和惯性积所需要参数(比如扭摆法中的扭杆系数[2-3],三线摆法中的空摆质量、摆长等)进行标定;3)提高产品测量位姿定位精度,这依赖于固定产品的机械工装加工和装配精度以及机械结构。对于中小型待测产品来说,由于测量设备体积小且机械结构简单,工装加工及装配精度可以达到较高的要求,因此通常情况下忽略产品位姿对测量精度的影响,只考虑前两个因素的影响。但是对于大型质量特性一体化测量设备来说,通常采用可两自由度旋转的连杆结构来实现位姿变换,机械加工以及装配所产生误差通过连杆的相对运动放大并传递至终端执行器,进而导致被测产品的位姿目标值与实际位姿之间的偏差较大。因此对于大尺寸箭弹质量特性测量来说,通过标定位姿以减小位姿误差对提高测量精度有着非常重要的意义。
1 运动学建模
产品位姿的变换依托于机械工装结构,如图1所示,这是一个串联型机械结构,工装上的2 个电机可分别带动产品进行横向和纵向两自由度的旋转,以实现变换不同测量位姿的需求。
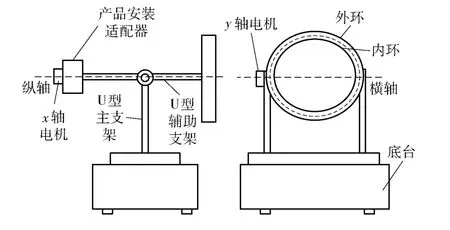
图1 机械工装示意图Fig.1 Schematic diagram of mechanical system
利用D-H 参数来建立机械结构的理想运动学模型。首先建立相关坐标系,如图2所示,建立参考坐标系Oxyz,选择横轴L1作为关节1,用z0表示,x0与参考坐标系x 轴方向一致,原点O0选择横轴中心点,根据右手法则建立关节1 的坐标系;选择纵轴L2作为关节2,用z1表示,x1垂直于z0和z1,O1与O0重合,利用右手法则建立关节2 坐标系O1x1y1z1,末端适配器坐标系也就是产品坐标系的坐标轴与关节1 坐标系坐标轴平行,原点为适配器上某一已知点。
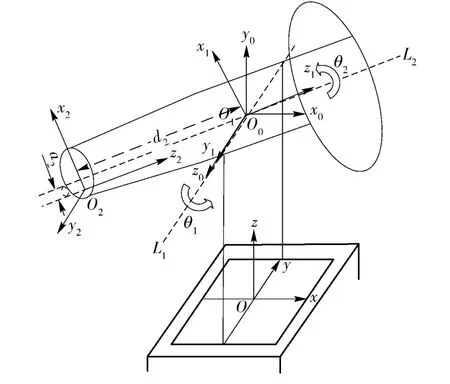
图2 连杆坐标系Fig.2 Coordinate frame of link-pole
建立坐标系后,从坐标系i -1 到坐标系i 的转换矩阵i-1Ti就可以用利用θ、d、a、α 这4 个D-H 参数并按照一定的顺序表示:
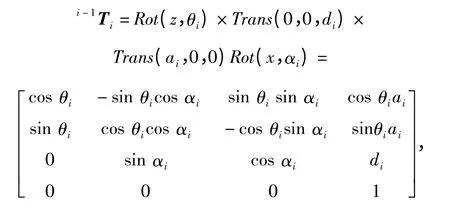
式中:θi为连杆夹角,即坐标轴xi-1与xi的夹角;ai为连杆长度,即坐标轴zi-1与zi的公垂线距离;di为连杆距离,即坐标轴xi-1与xi的公垂线距离;αi为连杆扭角,即坐标轴zi-1与zi的夹角。
从参考坐标系到产品坐标系的转换矩阵即产品位姿可记作:
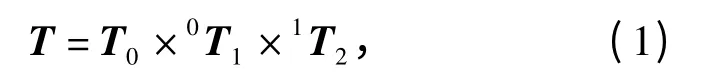
式中:T0是参考坐标系到坐标系O0x0y0z0的转换矩阵,是一个常数矩阵;0T1、1T2是含有D-H 参数的矩阵,只要已知θ=(θ1,θ2)和par=(di,ai,αi)就可以确定产品位姿T:
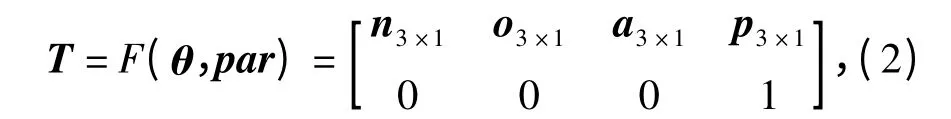
式中:n、o、a 分别是产品坐标系x、y、z 轴的方向向量;p 是坐标系原点坐标组成的列向量。
2 测量位姿对质量特性测量的影响
在测量质心时,产品需变换2 种位姿,然后分别将每个位姿下测得的数据转换到产品坐标系下,得到最终的结果:
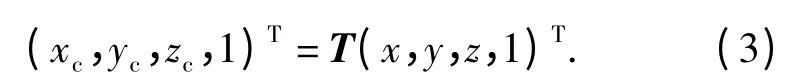
而在测量转动惯量和惯性积时,需要变换6 个位姿,联立6 个方程,得方程组:
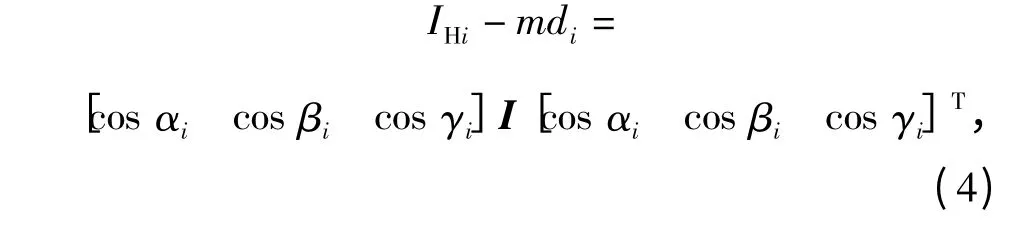
式中:αi、βi、γi分别是第i(i=1 ~6)个位姿下产品坐标系x、y、z 轴与扭摆轴的夹角;di是第i 个位姿下产品质心到扭摆轴的距离;I 为待测转动惯量和惯性积组成的惯性张量矩阵,
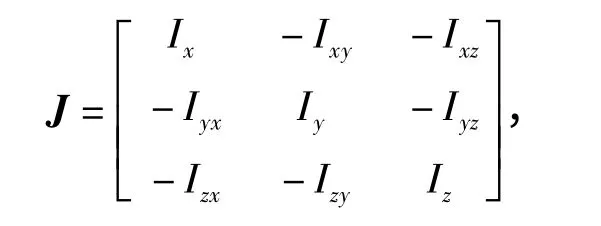
式中:Ixy=Iyx,Ixz=Izx,Iyz=Izy.
产品位姿产生偏差ΔT 会对测量结果产生如下影响:
2)质心位置的偏差会导致方程组(4)式中常数项矩阵中di存在偏差Δdi.
3)产品位姿偏差ΔT 中的姿态偏差或者叫旋转偏差[Δn,Δo,Δa],会产生Δαi、Δβi、Δγi变化。那么(4)式就变为
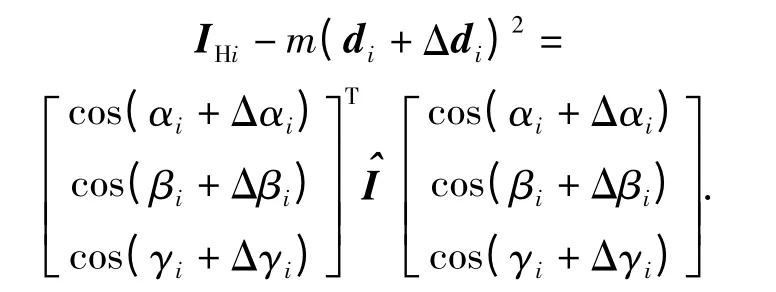
因此机械工装D-H 参数的准确与否直接影响产品测量位姿,进而影响测量结果的准确程度。
3 运动学标定法
由于工装D-H 参数以及运动角度都会有误差产生,因此产品的实际位姿为
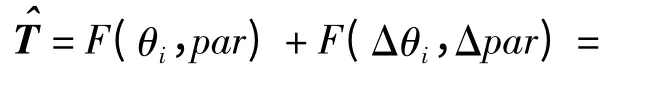
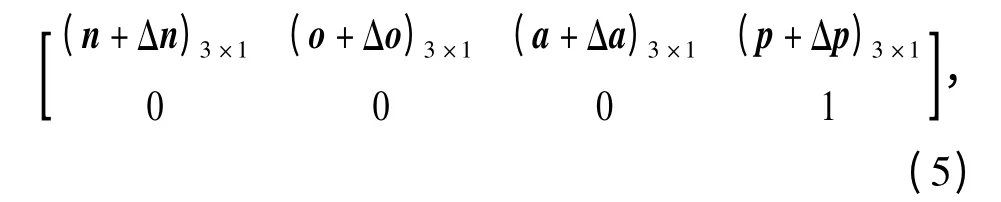
式中:Δn、Δo、Δa 为产品坐标系的姿态偏差(旋转偏差);Δp 为产品坐标系的位置偏差(平移偏差).
当实际几何参数与理论几何参数偏差较小时,位姿误差可简化成相应的线性模型[6]
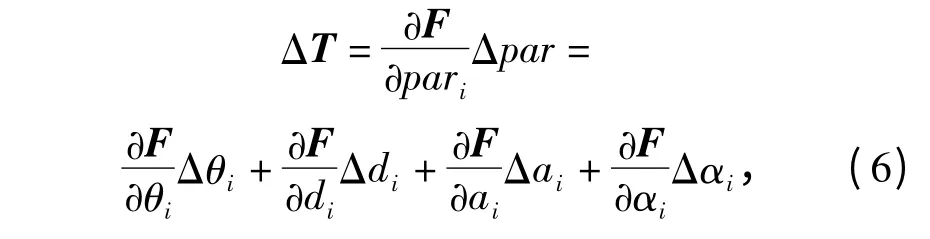
式中:Δdi、Δai、Δαi,是由于第i 个连杆的加工和安装精度导致的,一旦安装好后这些参数就为定值;而Δθi主要是由于工装重力因素和减速器齿轮之间的间隙造成的,属于非几何参数误差,且误差大小是随着旋转角度的变化而变化的。
将减速器中齿轮的间隙及偏心导致的角度误差记作Δθgi[7],Δθgi= P1gsin(αi+ φ1)+ P2gsin(niαi+φ2),式中:αi为关节旋转的角度;ni是减速器减速比;P1g、P2g、φ1、φ2为需要标定的参数。
机械工装自身重力和外加负载也会对该关节转角产生偏差,记作ΔθLi,将该柔性关节简化为线性扭簧模型,即ΔθLi=Cif(G,θi),式中:f(G,θi)为施加在柔性关节轴上的等效力矩;G 为连杆重力;Ci为需要标定的柔度系数。因此关节旋转角度的误差为
根据运动学的正解的原理[8],可以由(6)式得到产品坐标系上在任意位姿下的位置偏差与结构参数误差值的关系:

上式可以写成
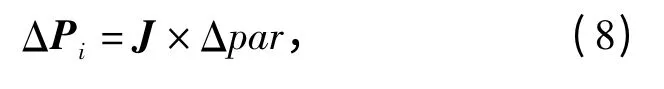
式中:矩阵J 为雅克比矩阵的一种变形形式,可视为参数误差的传递矩阵;ΔPi代表产品坐标系位置偏差,即标定点坐标的实际值Pr与名义值Pn的差。
标定过程如图3所示,将关节转角和待标定参数的名义值θn、parn代入到系统的运动学模型中,得到标定点位置的名义值Pn,同时根据关节转角将设备运动到指定位置,再利用激光跟踪仪测量标定点位置的实际值Pr,将位置偏差代入到(8)式,通过解非线性方程组,得到参数的误差值Δpar,将其代入(5)式得到产品的实际位姿。
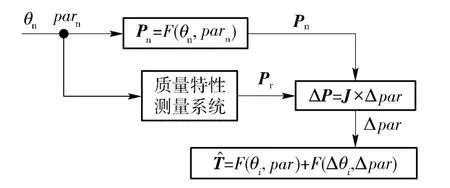
图3 运动学标定过程Fig.3 Kinematics calibration process
4 神经网络在位姿标定中的应用
运动学标定法虽然在原理上比较简单,但是需要考虑的影响因素较多,尤其是在关节旋转角误差的分析方面,其误差模型主要是通过经验公式和半经验公式得到的。这些方法都是要假设输入与输出之间存在一定的函数关系,这在理论上存在一定的缺陷,而且对于新出现的数据,经验公式不能较快地吸收来改进其本身的精度。因此采用神经网络方法来解决上述问题。
通过前文对运动学模型的分析,可以将参数误差分为两类:刚性参数误差和柔性参数误差。刚性参数误差就是D-H 参数中d、a、α 的误差,机械工装加工安装好以后,这些参数的误差就不发生变化了;而关节旋转角度θ 是一个变量,其误差是与当前角度有关的一个非线性变量,所以称之为柔性参数误差。下面对两种误差分别进行标定。
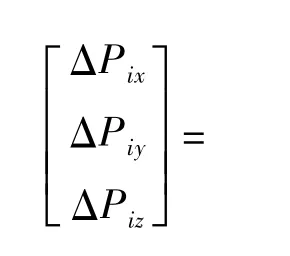
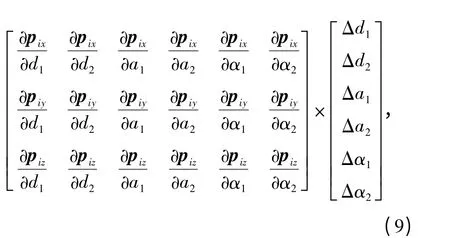
刚性误差仍利用运动学标定,标定原理及过程同上一节,在此不再赘述。最后得到产品坐标系位置偏差模型取N 个(N≥3)标定点坐标,代入(9)式,利用最小二乘原理解该线性方程组,就可得到刚性参数误差。
柔性参数误差则利用BP 神经网络进行标定,该网络共分3 层,第1 层为输入层,由两个神经元组成,分别为两个关节的旋转角θ1、θ2. 第2 层为隐层。第3 层为输出层,包含两个神经元Δθ1、Δθ2,代表关节的非几何参数误差。隐含层的传递采用S 形的正切函数,输出层传递函数采用线性函数,并利用梯度下降动量法训练该网络。
网络学习过程如图4所示,测量设备各关节按照名义角度θn旋转,利用激光跟踪仪测量运动后终端产品坐标系的实际位置Pr,将θn作为神经网络的输入数据,网络的输出数据Δθ 必须满足产品坐标系位置偏差不大于0.01 mm.
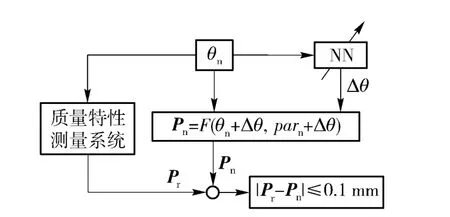
图4 网络学习过程Fig.4 The learning process of neural network
经过训练后的神经网络可以将各关节的旋转角度θ 和误差Δθ 的非线性关系建立起来。因此通过这种将神经网络与运动学相结合的方法标定后,可得到任意位姿下的设备结构参数误差Δθi和Δpar.将其值代入(5)式,就能得到产品坐标系的实际位姿。
5 标定实验过程及误差补偿结果
为了验证本文所述标定方法的有效性,进行了标定实验,如图5所示,利用控制台改变设备姿态,并利用激光跟踪仪进行关键点坐标的采集。根据标定原理,首先要选择若干组(θ1,θ2),实际关节的旋转角度范围为θ1∈[90°,180°],θ2∈[0°,360°]. 从初始位置开始关节1 按10°的间隔角进行运动,在关节1 的每个位姿下关节2 按45°的间隔角运动,最后在运动空间内共选取72 个标定位姿。

图5 利用激光跟踪仪进行标定试验Fig.5 Calibration experiment using laser tracker
利用运动学标定法来标定所有的参数,理论上16 个参数共需要6 个标定位姿就能得出结果,为了提高标定精度,从中选择20 个位姿进行标定;神经网络-运动学混合标定法中,同样利用其中的20 个位姿进行刚性参数的标定,然后选取整个空间72 个位姿进行神经网络的训练,进行柔性参数的标定。
为验证最终的标定效果,定义产品坐标系位置误差EL和姿态误差Ep为最后利用后20 个位姿来对比2 种方法的标定效果,如图6所示。
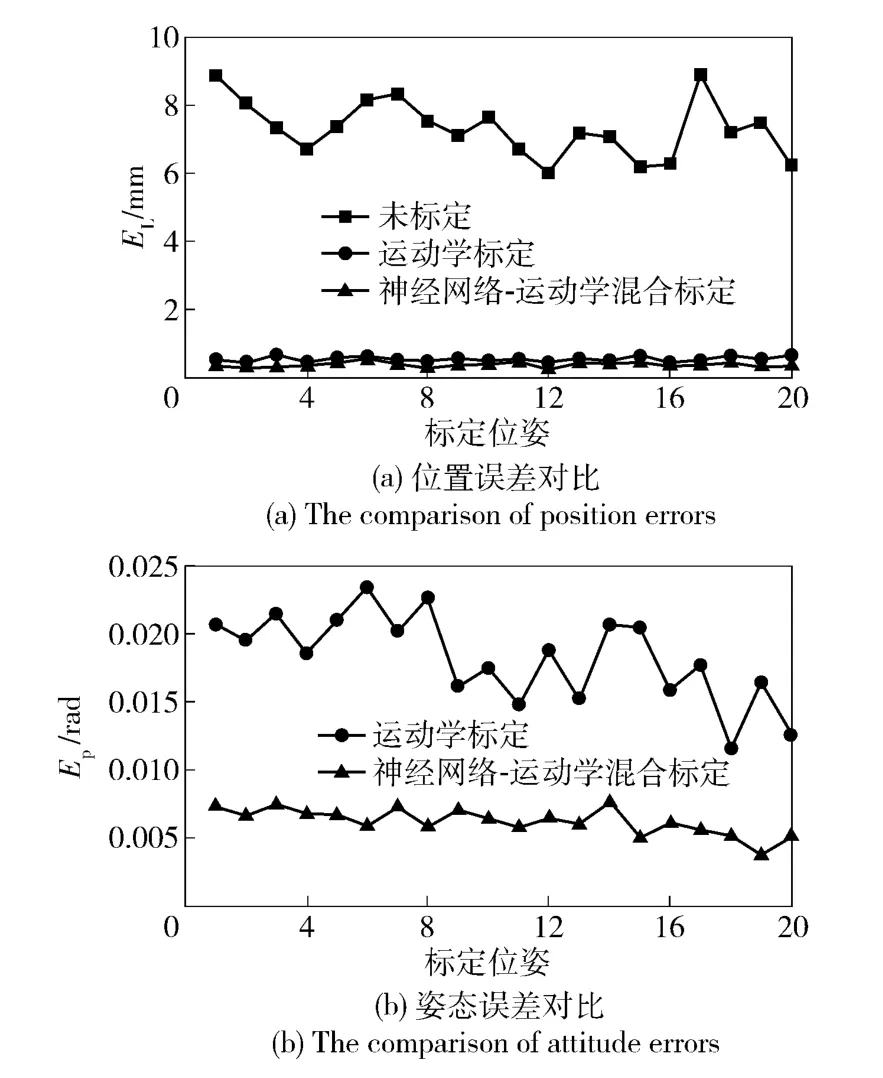
图6 标定结果对比Fig.6 The comparison of calibration results

表1 标准件质量特性测量结果对比Tab.1 Comparison of measurement results of mass properties of standard parts
从标定结果中可以明显看出,标定后的设备较未标定的设备位置误差明显减小,利用运动学标定后的设备位置误差平均值为0.565 8 mm,姿态误差的平均值为0.018 3 rad;而利用神经网络与运动学相结合的方法标定后的设备,其位置误差平均值为0.397 5 mm,姿态误差的平均值为0.006 2 rad. 可以看出后者的标定精度高于前者。
分别在采用两种标定方法进行位姿补偿的情况下测量并计算标准件的质量特性,得到结果如表1.通过实验对比,运动学标定法将质心测量误差减小为标定前的10%,转动惯量和惯性积测量误差减小为标定前的90%和20%;利用神经网络与运动学相结合的标定方法能将质心的测量误差减小为标定前的7%,转动惯量和惯性积测量误差减小为标定前的45%和15%.
6 结论
在大尺寸箭弹质量特性参数测量领域中,提高质量特性参数测量精度一直是研究的重点,而目前的方法对于大尺寸一体化质量特性测量系统具有局限性。因此本文从测量位姿对测量精度的影响出发,分别利用运动学标定方法和神经网络与运动学相结合标定法,通过对测量位姿的标定,提高了质量特性的测量精度。前者原理简单,具有普遍适用性——不同的待测产品只要测量设备不变就不需要重新标定;后者由于柔性误差受到待测产品本身的特性影响,因此针对不同的待测产品需要重新标定,但是其标定精度更高,更适合高精度测量。
References)
[1]潘文松,王昌明,包建东,等. 弹体质量、质心及质偏心测试误差补偿[J]. 机械工程师,2010(7):1 -2.PAN Wen-song,WANG Chang-ming,BAO Jian-dong,et al.Measurement error compensating for missile mass centroid and centroidal deviation[J]. Mechanical Engineer,2010(7):1 -2(in Chinese)
[2]吴斌,杨全洁. 用扭摆法测量导弹惯性积的误差分析[J]. 弹箭与制导学报,2005,25(4):153 -155.WU Bin,YANG Quan-jie. Error analysis for testing missile’s product of inertia using torsion pendulum[J]. Journal of Projectiles,Rockets,Missiles and Guidance,2005,25(4):153 -155.(in Chinese)
[3]张心明,王凌云,刘建河,等. 复摆法测量箭弹转动惯量和质偏及误差分析[J]. 兵工学报,2008,29(4):450 -453.ZHANG Xin-ming,WANG Ling-yun,LIU Jian-he,et al. The measurement of inertia moment and centroidal deviation of rocket projectile with compound pendulum method and its error analysis[J]. Acta Armamentarii,2008,29(4):450 -453. (in Chinese)
[4]王超,唐文彦,张晓琳,等. 大尺寸非回转体质量特性一体化测量系统的设计[J].仪器仪表学报,2012,33(7):1634 -1639.WANG Chao,TANG Wen-yan,ZHANG Xiao-lin,et al. Design of mass property integration measurement system for large size nonrotatinig bodies [J]. Chniese Journal of Scientific Instrument,2012,33(7):1634 -1639.(in Chinese)
[5]李慧鹏,唐文彦,张春富,等.导弹转动惯量测试系统及误差分析[J]. 兵工学报,2007,28(2):206 -208.LI Hui-peng,TANG Wen-yan,ZHANG Chun-fu,et al. A measuring system of inertia moment of missile and its error analysis[J].Acta Armamentarii,2007,28(2):206 -208. (in Chinese)
[6]Wu C H. The kinematic error model for the design of robot manipulators[C]∥American Control Conference. San Francisco:IEEE,1983:497 -502.
[7]Judd R P,Knasinski A B. A technique to calibrate industrial robots with experimental verification[J]. IEEE Transactions on Rototics and Automation,1990,6(1):20 -30.
[8]任永杰,邾继贵,杨学友,等. 利用激光跟踪仪对机器人进行标定的方法[J]. 机械工程学报,2007,43(9):195 -200.REN Yong-jie,ZHU Ji-gui,YANG Xue-you,et al. Method of robot calibration based on laser tracker[J]. Chinese Journal of Mechanical Engineering,2007,43(9):195 -200. (in Chinese)
[9]Aoyagi S,Kohama A,Nakata Y,et al. Improvement of robot accuracy by calibrating kinematic model using a laser tracking system-compensation of non-geometric errors using heural hetworks and selection of optimal measuring points using genetic algorithm[C]∥Intelligent Robots and Systems (IROS),2010 IEEE/RSJ International Conference on IEEE. Taipei,Taiwan:IEEE,2010:5660 -5665.

