SSG模型在压缩拐角激波/湍流边界层干扰模拟中的应用

张常贤，闫文辉，徐晶磊

(1.中航空天发动机研究院基础研究中心，北京100028；2.中国航空研究院，北京100012；3.北京航空航天大学能源与动力工程学院，北京100191)

SSG模型在压缩拐角激波/湍流边界层干扰模拟中的应用

张常贤1，闫文辉2，徐晶磊3

(1.中航空天发动机研究院基础研究中心，北京100028；2.中国航空研究院，北京100012；3.北京航空航天大学能源与动力工程学院，北京100191)

采用非线性方案模化雷诺应力再分配项的二阶矩雷诺应力输运模型——SSG模型和两方程线性涡粘模型SST模型，对24°高雷诺数二维压缩拐角激波/湍流边界层相互干扰流动进行数值模拟。通过在壁面压力分布、壁面摩擦阻力系数分布、截面速度分布及分离区大小等方面与实验数据比较，综合评估了上述两种模型模拟该问题的能力。结果表明：两种湍流模型在上述各方面都取得了与实验较为一致的结果，但相比较而言，除SST模型在流动再附后对壁面摩擦阻力系数分布的模拟更接近实验值外，SSG模型结果在上述其他方面均更接近实验值。本文工作为压缩拐角激波/湍流边界层干扰这类流动数值模拟的湍流模型选择提供了参考。

SSG模型；SST模型；压缩拐角；激波；湍流边界层；压力应变关系

1 引言

在诸多形式的湍流模型中，雷诺应力输运模型不同于涡粘湍流模型，其直接对湍流脉动应力建立微分形式的输运方程并模化求解，能更真实地反映湍流机理。其中，压力应变项Πij的存在是雷诺应力模型最显著的特点。该项影响湍动能再分配但不会产生脉动能量，因此又称为雷诺应力再分配项。由于该项在确定复杂湍流结构方面起着关键作用，故对其合理模化是保证二阶矩雷诺应力模型准确预测的基础[1]。Rotta[2]、Launder等[3]先后对Πij进行了模化研究，开发了采用线性方案的LRR-IP模式[4]。该模式后来成为雷诺应力输运方程基准模式。后续研究中，Lumley[5]证明了采用非线性形式的必要性，推导了基于各向同性张量性质的雷诺应力输运方程，其再分配项包含了二次项的形式，在高雷诺数和低各向异性条件下可降为LRR-IP模式。1992年，Spe⁃ziale等在非线性形式的基础上发展了SSG模型[1]。此模型基于张量不变量的函数性质，同时充分考虑均匀湍流的连续性特点，以一阶泰勒级数展开的形式，结合量级分析对再分配项的常系数做替换得到。Abid[6]、Jakirlic[7]、于意奇[8]和仇璐珂[9]等采用SSG湍流模型，数值模拟了凸包流动、翼型绕流、叶栅内流和内通道冷却流等，所得结果与实验吻合较好。

压缩拐角激波/湍流边界层干扰现象普遍存在于气体的高速流动中。如当飞行器处于超声速飞行状态时，在飞行器进气道口，压气机叶片与轮毂交界，以及飞行器外表面的机翼、机身舵面上，都存在着这种流动现象。在压缩拐角流动中，来流面对的拐角挤压结构诱导激波产生，接着激波与湍流边界层相互作用破坏了流动平衡状态而在拐角处产生分离等复杂流动现象。该问题涉及到湍流的逆压流动、非平衡状态、分离流动、旋转等一系列复杂情况，是理想的验证算例，常被用来检验可压缩湍流模型的综合预测能力。目前，国外很多相关的研究者已针对此类问题做了比较细致的研究。Settles[10～13]等在普林斯顿大学高雷诺数超声速风洞，研究了多角度高雷诺数压缩拐角干扰流动在激波湍流边界层相互干扰作用下，所呈现的从附着、产生分离到产生显著分离等多种流动形态。Elfstrom[14]、Fernholz[15]和Zheltovodov[16]等也都进行了大量相关实验，为研究压缩拐角流动提供了丰富的数据依据。针对这类问题的数值模拟研究已经开展，并在飞行器设计过程中起到越来越重要的作用。如何选用湍流模型能给出较为精确的数值预测，将对后续的飞行器设计研究具有重要意义。

本文采用SSG模型进行压缩拐角激波/湍流边界层干扰流动数值模拟。为了考察其与传统湍流模型的区别，还选用涡粘模式的两方程模型——SST模型[17]一同进行数值模拟，对比分析两种湍流模型在压缩拐角激波/湍流边界层干扰流动中，在壁面压力分布、壁面摩擦阻力系数分布、截面速度分布及分离区大小等方面体现出的各自特性。

2 控制方程及数值方法

2.1 控制方程

基本控制方程为可压缩Favre平均N-S方程，其守恒形式为：

2.2 SSG模型

压力应变项一般可表达成快速项与慢速项之和的形式，但经一系列数学变换[1]，其二次方形式在平板均匀湍流的情况下可写成式(9)的形式。

考虑到均匀湍流流动中各种情形下的渐近连续性及湍流脉动各向异性的特点，Speziale等在保留压力应变项原有形式的同时，将Aij和Mijkl写成以bij为变量的泰勒级数展开的形式并保留第一阶导数。具体方法是将c3用替代，c1用替代。则式(9)修改之后的形式为：

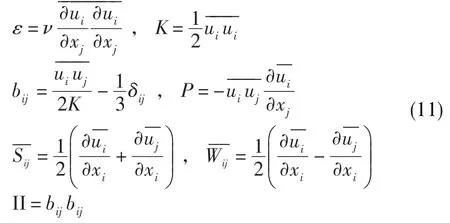
2.3 计算方法

本文所使用的计算程序为自编程序，采用有限体积法对可压缩Favre平均N-S方程和湍流模型输运方程进行离散求解，湍流模型分别选用SSG模型和SST模型。为提高激波位置捕捉精度，无粘通量离散采用矢通量分裂Roe[18]格式。为获得高阶的Roe格式，单元界面的流动参数由三阶MUSCL插值公式构造[19，20]。为抑制激波附近解的过冲或膨胀现象，采用minmod限制器。粘性通量采用中心差分格式。时间离散采用Jameson五步Runge-Kutta显式时间推进格式。

3 计算结果及分析

3.1 模型建立

采用Settles等在普林斯顿大学超声速风洞进行的二维24°压缩拐角实验为算例进行数值模拟[10～13]。该实验在其一系列压缩拐角实验中拐角角度最大，流动现象最为丰富。

实验条件：来流马赫数Ma∞=2.84，总温T0=262 K，壁温Tw=276 K，总压p0=6.89×105Pa，特征边界层厚度δ=23 mm，基于单位长度的来流雷诺数Re=6.3× 107。分别针对网格数为130×80、180×110、170×160和230×180进行了网格无关解验证，其中后面三种网格所得数值模拟结果基本一致，而第一种网格的结果有些差距。因此下面计算结果均基于180×110网格。此时最底层网格法向尺寸为2.0×10-7m，可保证y+＜1。本算例中，超声速气流流到拐角处由于斜坡压缩作用产生系列压缩波并汇集为激波。激波后边界层变厚，速度降低，逆压梯度增加。另外，由于拐角角度过大，流动在激波后产生分离。在超声速流动区，流场信息无法向上游传递。在边界层内亚声速流动区，激波后的大逆压梯度向上游反馈信息，增加激波前压强并引起边界层厚度增加，最终迫使激波前移至新的位置形成平衡。流体在绕过分离区后再附，并继续向前流动，形成新的压缩波区。流动示意图如图1所示。

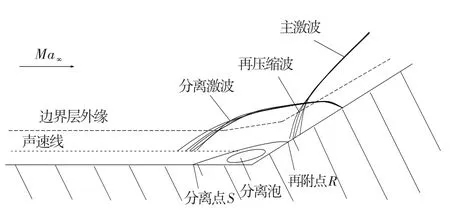
图1 压缩拐角激波/湍流边界层干扰流动模型Fig.1 The scheme of shock wave/turbulence boundary layer interaction

3.2 结果及分析

压缩拐角激波/湍流边界层干扰问题，主要关注分离和再附位置、分离区长度、激波位置、壁面摩擦力及截面速度分布。下面结合文献[9]中实验数据，对SSG模型与SST模型计算结果进行评测。

3.2.1 分离区

两种模型都模拟出了流动分离现象，具体流动分离及再附点位置见表1。可见，两种模型都成功预测出了流动分离，都对压缩拐角问题具有一定的模拟能力，但对分离与再附点的预测差别较大。SSG模型较为准确地预测了分离点的位置，而SST模型预测的偏差较大，分离点提前了近一倍；对再附点位置的预测，与实验值相比，SSG模型的有所提前，而SST模型预测结果严重滞后。

表1 分离位置区及分离区长度Table 1 Separation locations and length

图2描绘了两种模型所预测的分离区附近的流线图。从分离区范围看，SSG模型所预测的更接近实验测量，而SST模型预测结果大于实验测量值。总体而言，虽然两者预测的结果都与实验值有一定差距，但SSG模型的预测结果明显优于SST模型。

3.2.2 壁面压力分布

图3示出了计算所得壁面压力分布与实验值的对比情况，其中零点对应位置为拐角点处。可见，SSG模型模拟结果较为准确，无论是激波开始位置还是拐角处的压力分布曲线，都与实验测量结果吻合较好，不足之处在于对拐角斜面末端的预测略低于实验值。相比之下，SST模型的表现不够理想，计算所得激波位置过于靠前，而拐角之后的压力分布整体偏低。其原因是：算例中SST模型对湍流粘性的预计不足，造成流动过早分离，激波位置靠前和过迟再附，并伴随压力恢复不足。

图2 流场分离区流线图Fig.2 Stream-trace patterns at the separation zone

图3 壁面压力Fig.3 Surface pressure distribution

3.2.3 流向截面速度分布

图4示出了沿流向截面的速度分布。可见，x/δ0=-3.012位于分离之前，两个模型都得到了较好结果；但随着流动的发展，SST由于对湍流粘性预测不足，出现过早分离。从位置2开始，SST所预测截面速度型与实验出现偏差。直到位置5速度型在外缘部分开始与实验值相比之前吻合良好。SSG的预测结果明显优于SST的预测结果，但在拐角前相比实验仍有一定差距。原因为雷诺应力预测偏大，这也正是其速度型明显要比实验值更饱满的原因，特别是在边界层中部尤为明显。由于拐角后面的速度型对应的都是实验再附后的位置，此时SSG的分离也已经结束，因此又得到了较好结果。相比之下，SST在拐角后和在拐角前的问题一样，对湍流粘性的预测不足。对于拐角后的第一个测量点，实验中流动已经再附，而SST还处于流动分离状态，这直接影响了其预测准确性。从后续测量点的比较中可以看到，SST所预测的速度型在靠近壁面处相比实验测量亏损较大。

图4 沿流向截面的速度分布Fig.4 Streamwise velocity profiles at different stations

3.2.4 壁面摩擦阻力系数分布

壁面摩擦阻力是体现湍流模型预测能力的一个重要参数。两种湍流模型在对壁面摩擦阻力系数分布预测中的表现如图5所示。可见，对于拐角前摩擦阻力系数开始减小的位置，SSG模型预测结果比实验值稍为滞后，而SST模型比实验值提前且差距稍大。在分离区内，SSG模型率先达到最小值并开始回升，其具体位置也与实验值一致；而SST模型却继续降低到一个更小的数值，其直接影响就是对再附点位置的预测产生较大误差。再附后的流动中，SSG模型迅速增加并超过实验值，且随着流动的发展这种差距越来越大。SST模型的再附位置更靠后，且一直保持小于实验值发展，但更为接近实验值。综合看，在摩擦阻力系数的预测中，两种模型各有优缺点，流动再附前SSG表现较好，再附后则相反。

4 结论

SST模型与SSG模型，都能成功模拟出高雷诺数二维压缩拐角激波/湍流边界层相互干扰流动中的流动分离与再附等现象。但相比较而言，除SST模型在流动再附后对壁面摩擦阻力系数分布的模拟更接近实验值外，SSG模型结果在其他方面均更接近实验值，更适应于此类型流动。具体为：

(1)SSG模型和SST模型都成功预测了流动分离。SSG模型很好地预测出分离位置，但对于再附位置则有轻微提前；SST模型由于对湍流粘性预测不足致使分离位置提前，分离区过大，再附点严重滞后，预测结果不理想。

(2)SSG模型预测的激波位置与实验结果基本吻合，SST模型预测的激波位置由于流动分离则明显提前。

(3)SSG模型较好地预测出各截面处速度型，特别是在拐角后预测结果与实验值吻合得更好。而SST模型的预测速度型在拐角前相比实验结果较为亏损，到流动再附后才有所好转，亏损区域只集中在靠近壁面的区域，在边界层外缘符合较好。出现该现象的原因是由于SST模型对湍流粘性预测不足。

(4)两个模型对壁面摩擦阻力系数的预测都没有得到很准确的结果。SSG模型对流动再附后的摩擦阻力系数预测结果与实验值相差很大；SST模型在流动再附后一段位置较SSG模型预测结果更接近实验值，但在其他区域表现较差。

[1]Speziale C G，Sarkar S，Gatski T B.Modeling the Pres⁃sure-Strain Correlation of Turbulence:An Invariant Dy⁃ namical Systems Approach[J].Journal of Fluid Mechanics，1991，227：245—272.

[2]Rotta J C.Statistische Theorie Nichthomogener Turbulenz [J].Z.Phys，1951，129(6)：547—572.

[3]Launder B E，Reece G，Rodi W.Progress in the Develop⁃ment of a Reynolds Stress Turbulence Closure[J].Journal of Fluid Mechanics，1975，68：537—566.

[4]张兆顺，崔桂香，许春晓.湍流理论与模拟[M].北京：清华大学出版社，2005.

[5]Lumley J L.Turbulence Modeling[J].Journal of Applied Mechanics，1983，50(4b)：1097—1104.

[6]Abid R，Morrison J H，Gatski T B，et al.Prediction of Aerodynamic Flows with a New Explicit Algebraic Stress Model[J].AIAA Journal，1996，34(12)：2632—2635.

[7]Jakirlic S，Eisfeld B，Jester-Zürker R，et al.Near-Wall, Reynolds-Stress Model Calculations of Transonic Flow Configurations Relevant to Aircraft Aerodynamics[J].Inter⁃national Journal of Heat and Fluid Flow，2007，28(4)：602—615.

[8]于意奇，顾汉洋，杨燕华，等.稠密栅元不同子通道内湍流流动的RANS和URANS模拟[J].原子能科学技术，2011，45(10)：1191—1197.

[9]仇璐珂，王新军，韩宇萌，等.蛇型冷却通道中的蒸汽流动与换热特性研究[J].空气动力学学报，2011，29(2)：235—239.

[10]Settles G S，Vas I E，Bogdonoff S M.Details of a Shock-Separated Turbulent Boundary Layer at a Compres⁃sion Corner[J].AIAA Journal，1976，14(12)：1709—1715.

[11]Settles G S，Fitzpatrick T J，Bogdonoff S M.Detailed Study of Attached and Separated Compression Corner Flowfields in High Reynolds Number Supersonic Flow[J].AIAA Jour⁃nal，1979，17(6)：579—585.

[12]Settles G S.An Experimental Study of Compressible Tur⁃bulent Boundary Layer Separation at High Reynolds Num⁃ber[D].Princeton：Princeton University，1975.

[13]Settles G S，Dodson L J.Hypersonic Shock/Boundary-Lay⁃er Interaction Database[R].NASA CR-177577，1991.

[14]Elfstrom G M.Heat Transfer from Hypersonic Turbulent Flow at a Wedge Compression Corner[J].Journal of Fluid Mechanics，1972，53(1)：113—127.

[15]Fernholz H H，Finley P J，Dussauge J P，et al.A Survey of Measurements and Measuring Techniques in Rapidly Dis⁃tortedCompressibleTurbulentBoundaryLayers[R]. AGARDograph 315，1989.

[16]Zheltovodov A A，Trofimov V M，Schuelein E，et al.An Ex⁃perimental Documentation of Supersonic Turbulent Flows in the Vicinity of Sloping Forward-and Backward-Facing Ramps[R].USSR：Institute of Theoretical and Applied Me--chanics，USSR Academy of Sciences，1990.

[17]Wilcox D C.Reassessment of the Scale Determining Equa⁃tion for Advanced Turbulence Models[J].AIAA Journal，1988，26(11)：1299—1310.

[18]Roe P L.Approximate Riemann Solvers,Parameter Vec⁃tors,and Difference Schemes[J].Journal of Computational Physics，1981，43(2)：357—372.

[19]Van Leer B.Towards the Ultimate Conservative Difference Scheme V:A Second Order Sequel to Godunov’s Method [J].Journal of Computational Physics，1979，32：101—136.

[20]Anderson W K，Thomas J L.Comparison of Finite Volume Flux Vector Splitting for the Euler Equation[J].AIAA Jour⁃nal，1986，24(9)：1453—1460.

Application of SSG Model to Shock-Wave/Turbulent Boundary-Layer Interaction Flow at a Compression Corner

ZHANG Chang-xian1，YAN Wen-hui2，XU Jing-lei3
(1.China Aerospace Engine Establishment，Beijing 100028，China；2.Chinese Aeronautical Establishment，Beijing 100012，China；3.School of Energy and Power Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100091，China)

Numerical investigations on shock-wave/turbulent boundary-layer interaction flow at compres⁃sion corner were carried out using both SSG model and SST model.The results were compared with experi⁃ment data,including the pressure distribution,friction coefficients on the wall and velocity profiles at differ⁃ent positions,in order to evaluate which model was better.The results indicate that the SSG model gives a better performance for compression corner compared with SST model,but the simulation results of friction coefficient on the wall by SST model is closer to the experiment data.This investigation is referential to choose the turbulence model simulating shock-wave/turbulent boundary layer interaction flow.

SSG model；SST model；compression corner；shockwave；turbulent boundary layers；pressure-strain correlation

V211.3

：A

：1672-2620(2014)03-0001-05

2013-10-16；

：2014-06-02

张常贤(1981-)，男，江苏丰县人，工程师，博士，主要从事湍流模型数值研究。