某液压张紧器阻尼特性的数学建模与有限元验证*

胡玉梅,韩鲁强,刘 进,向以轩

(1.重庆大学，机械传动国家重点实验室，重庆 400044; 2.汽车噪声振动和安全技术国家重点实验室，重庆 400039)

前言

目前轿车发动机轮系中最常使用的自动张紧器主要分为干摩擦式和液压式两类。与干摩擦式自动张紧器相比，液压式自动张紧器能产生更大的阻尼，运行更平稳，且无噪声[1]。此外，选用液压式自动张紧器可以降低轮系的预张紧力，进而可以提高皮带和轴承的使用寿命[2]。

文献[3]中通过实验分析了液压张紧器的动态特性，建立了精确的模块化仿真模型，并在此基础上研究了温度和工作频率对张紧器工作状态的影响；文献[4]中利用AVL软件建立了采用液压式张紧器的发动机链传动机构的多刚体模型；文献[5]中利用实验手段对比研究了干摩擦式自动张紧器和液压式自动张紧器对前端轮系传动误差和皮带打滑的影响。

上述研究并未针对液压张紧器的阻尼性能进行深入探讨。本文中采用理论分析方法，建立了一种液压张紧器的数学模型，通过求解液压张紧器在简谐位移激励下的最大阻尼力和每周期所消耗的阻尼能来衡量液压张紧器阻尼特性；并采用有限元仿真对所建立的数学模型进行了验证。此液压张紧器数学模型的推导过程具有普遍意义，可有效指导类似液压张紧器的结构分析和设计。

1 张紧器结构与阻尼形成原理

图1为一典型的发动机附件轮系布置图，张紧装置总成由张紧轮、摇臂和液压张紧器3部分组成，布置在皮带的松边上。张紧器下端通过铰链连接到发动机机体上，上端与摇臂相连。摇臂的旋转运动最终转化为张紧器的上下往复运动。

图2为液压张紧器结构和工作原理示意图。该液压张紧器由活塞、活塞杆密封、活塞导向座、压缩弹簧、橡胶波纹密封和单向阀等组成。其中活塞导向座通过卡环随活塞运动，并将压缩弹簧的反作用力传递到活塞上。活塞杆密封用来防止油腔内油液泄漏到橡胶波纹密封腔内，气体可在橡胶波纹密封腔和油腔间流动。橡胶波纹密封可防止空气泄漏，保持油腔内压力，并排除外界环境对油液的污染。

在张紧器工作过程中，活塞被压缩至某一平衡位置并在平衡位置附近作微幅往复运动。活塞向下运动时，单向阀将高压腔与低压腔隔开，高压腔压力升高，液压油通过泄油间隙(即环形阻尼缝隙)被挤入低压腔。活塞向上运动时，高压腔内压力降低，单向阀打开，低压腔内的液压油被吸入到高压腔。

在此过程中，活塞在张紧器内受到的力主要有两个：一是压缩弹簧的反力，二是高压腔对活塞的压力。由于弹簧不是耗能元件，因此可以认为高压腔对活塞的压力即为阻尼力。在活塞向下运动时，高压腔压力方向和活塞运动方向相反，对活塞做负功；在活塞向上运动时，高压腔压力方向和活塞运动方向相同，对活塞做正功。由于活塞向下运动时高压腔压力远大于活塞向上运动时的压力，故活塞在往复运动中会消耗大量的能量。在此定义阻尼力为活塞在高压腔受到的压力，阻尼能为活塞一个运动周期所消耗的能量。

2 张紧器阻尼特性数学模型的建立

为准确计算液压张紧器在一个运动周期中消耗的阻尼能和产生的最大阻尼力，须对进、出高压腔的油量进行分析，并建立高压腔油压的微分方程；为准确表示流经单向阀的流量，须计算出单向阀开度，进而还须建立单向阀小球的运动微分方程。利用数值方法对高压腔油压微分方程和单向阀运动微分方程联立求解，即可得到任意时刻高压腔内的压强和阻尼力示功曲线，进而计算出张紧器的阻尼能和最大阻尼力。

2.1 高压腔油压微分方程的建立

为分析液压张紧器阻尼特性，建立如图2(b)所示的简化分析模型。图中：d为活塞直径；e为泄油间隙，即高压腔与活塞半径之差；l为泄油间隙的长度；h为高压腔的长度。高压腔压力为p1，低压腔压力为p2。由于活塞在平衡位置附近作微幅往复运动，低压腔体积变化可以忽略，分析中假设p2为常数。活塞杆受到幅值为A的强制位移激励。通过泄油间隙流出高压腔的体积流量为Q1，通过单向阀流入高压腔的体积流量定义为Q2。为方便起见，规定油液流入高压腔，流量为正值，油液流出高压腔，流量为负值。

根据液压流体力学相关理论，考虑偏心的圆柱圆环缝隙的流量计算公式[6]为

(1)

式中：μ为液压油动力黏度；ε为偏心率，ε=δ/e，δ为偏心距；v为活塞运动速度。

图3为单向阀结构示意图，当单向阀关闭时，Q2=0；当单向阀打开时，油液从低压腔通过单向阀进入高压腔，将此流动视为薄壁小孔出流，根据薄壁小孔流量计算公式[7]：

(2)

式中：AQ为单向阀最小流通面积；Cd为出流系数，在此取Cd=0.6[8]。

当单向阀开度不同时，流通面积的大小也在变化，因此AQ是单向阀小球升程xb的函数。根据参考文献[8]，单向阀流通面积的计算公式为

(3)

其中：

(4)

式中：db为单向阀小球的直径；ds为单向阀出口的直径。

液压传动中，当压力较高和进行动态计算时须考虑液体的可压缩性[9]。根据质量守恒定律，单位时间进出高压腔的油液体积流量与高压腔容积变化之差应等于高压腔油液密度变化所导致的体积变化量，即

(5)

其中高压腔容积:

(6)

根据液体体积模量的定义：

(7)

单位时间内高压腔容积变化相当于高压腔截面积与单位之间内活塞位移之积：

(8)

活塞的运动微分方程可表示为

(9)

综合式(5)、式(7)～式(9)即可得到高压腔油压的微分方程：

(10)

实际工作过程中，由于油液中混有空气，油液的体积模量E并非常数，会随着高压腔压力的变化而变化[10]，计算公式为

(11)

式中：Φgas0为一个大气压下空气在油液中的体积分数；patm为标准大气压；n为气体多变指数；Eoil为一个大气压下纯油液体积模量。

2.2 单向阀小球运动微分方程

图4为单向阀工作状态。单向阀小球运动过程中，共有3种受力状态：小球与下限位接触(图4(a))，小球不与上下限位接触(图4(b))，小球与上限位接触(图4(c))。

将上下限位作为大刚度大阻尼弹簧来模拟。大刚度是为阻止小球运动，起到限位的作用；大阻尼是为防止因将限位设置成弹簧而引起振动。忽略小球受到的油液黏滞力，质量为mb的小球受到的力包括单向阀弹簧力Fk1，上限位弹簧力Fk2，下限位弹簧力Fk3，上限位阻尼力Fc2，下限位阻尼力Fc3和压差力Fp。根据牛顿第二定律，建立单向阀小球运动微分方程为

(12)

其中

Fk1=-k1(xb+x0)

(13)

(14)

(15)

(16)

(17)

Fp=π(ds/2)2(p2-p1)

(18)

式中：k1为单向阀弹簧刚度；x0为单向阀弹簧预压缩量；xbmax为单向阀小球最大升程；k2、k3分别为上、下限位弹簧刚度，取值均为10 000N/mm；c2、c3分别为上、下限位阻尼系数，取值均为1N·s/mm。

2.3 数学模型的求解方法

联立式(9)，式(10)，式(12)，即可得到微分方程组：

(19)

在方程组中，v相当于外界对活塞杆的强制速度激励。参照我国减振器台架试验标准JB3901—85的规定，“测试减振器示功特性时，活塞相对于工作缸应做简谐运动”。因此张紧器阻尼特性数值计算中施加在活塞杆上的强制速度激励为

v=2πfAsin(2πft)

(20)

表明活塞运动速度是频率为f的正弦函数，即活塞受到幅值为A的简谐位移激励。

选取合适的初始条件，通过对微分方程组(19)进行数值积分求解，即可得到任意时刻高压腔内压强。根据式(21)，即可计算出活塞受到高压腔的压力F，即液压张紧器任意时刻受到的阻尼力为

F=(d/2)2πp1

(21)

3 数学模型的验证

为了验证数学模型的正确性，利用ADINA软件针对液压张紧器关键部分建立了流固耦合有限元模型。有限元仿真和理论计算采用了相同的边界条件和材料模型假设。不同之处在于：(1)有限元当中建立了上下限位的结构模型，并通过其与小球的接触来模拟上下限位对小球的作用力，数学模型是利用弹簧来模拟上下限位作用的；(2)有限元仿真根据计算流体力学的理论计算流量压力关系，而数学模型通过经验公式并配合流量系数的选择来进行计算。与理论计算相比，有限元仿真更接近于真实流动情况，可以看做数值实验。

液压张紧器高压腔部分是旋转轴对称结构，因此建立其二维旋转轴对称模型。

流体部分有限元模型如图5所示，高压腔壁使用壁面边界模拟，活塞用移动壁面边界模拟，并在其上施加幅值为0.5mm的简谐位移激励。对称轴上施加的是带有滑动条件的壁面边界，以模拟旋转轴对称边界。由于低压腔压强很小，而高压腔的压强最大值可达到20～30MPa，而且当弹性模量取值为常数时，低压腔的压强对液压张紧器消耗的阻尼能没有影响。为简化模型，将单向阀补油道的入口和阻尼缝隙的出口设置为自由边界，等效于低压腔压强p2设置为0MPa。

结构部分有限元模型如图6所示。小球受到的限位作用通过定义与上下限位间的接触来实现。单向阀的开闭通过在流体模型中设置GAP边界条件实现。通过对上限位施加位移约束来调节小球的最大升程。

流固耦合边界是流固耦合计算过程中结构模型与流体模型进行信息交换的界面，在有限元建模过程中，必须分别在结构模型和流体模型中将对应的边界面定义为流固耦合边界。结构模型和流体模型中的流固耦合界面在几何位置上应是重合的，且最好大小一致。分别在流体模型和结构模型中建立了流固耦合边界(见图5和图6)。

为了与有限元计算结果对比，数学模型中所有结构参数和流体材料设置与有限元中一致，如表1和表2所示。

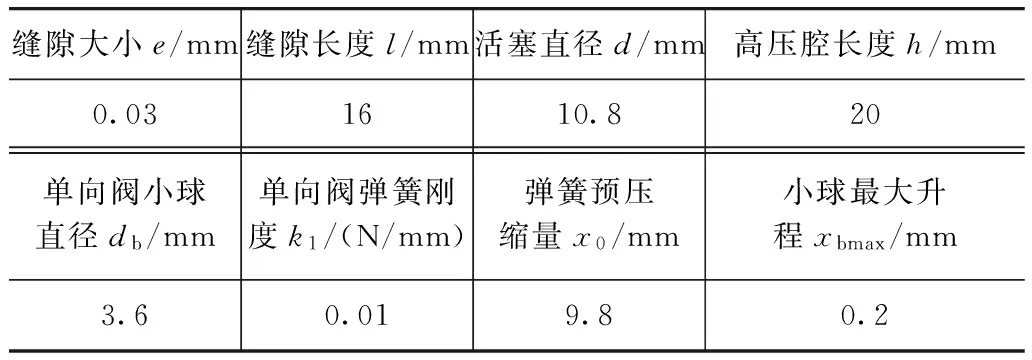
表1 张紧装置各结构参数

表2 油液材料参数

通常情况下，各类手册、文献建议在设计和分析液压系统时，忽略体积模量随压力的变化而采用有效体积模量，有效体积模量取值一般为700～1 400MPa[11]。在数学模型验证计算中，为了保持材料模型的一致性，忽略式(11)，设E为700MPa。

结合张紧器的实际工作情况，对激励为20～200Hz、间隔为10Hz的19种工况进行了有限元计算和理论计算。图7为激励为50Hz时的示功图对比。由图可见，两条示功曲线的形状非常接近；从示功图上可以直接读出两个最大阻尼力：数学模型计算为2 002.9N，有限元仿真为2 083.3N，相对误差3.9%；通过数值方法计算出示功图曲线围成的面积，即得到液压张紧器在一个工作周期内消耗的能量——阻尼能。数学模型计算得到的阻尼能为912.03mJ，有限元仿真模型得到的阻尼能为919.64mJ，相对误差0.75%。

其它各频率下最大阻尼力和阻尼能结果的对比如图8和图9所示。从图中可以看出，理论计算结果与有限元计算结果趋势基本一致，激励频率为20Hz时阻尼力出现最大峰值误差4.5%，激励频率为200Hz时阻尼能出现最大误差3.2%。由此可知，理论计算与有限元仿真结果吻合较好，本文中推导的理论模型正确。

4 阻尼能计算结果分析

由图8还可进一步看出，随着激励频率升高，最大阻尼力增大，但逐渐趋于平缓。而由图9则可发现，当激励频率在20～40Hz之间时，阻尼能随频率的增大而增大；当激励频率在40～200Hz之间时，阻尼能随频率的增大而减小。对于本文中所设定的参数，其阻尼能的峰值频率出现在40Hz左右。

为了研究阻尼能峰值频率和设计参数间的关系，计算了不同阻尼缝隙大小和长度时阻尼能随激励频率变化。

仅改变模型中缝隙的长度，发现随着缝隙长度的增加，阻尼能峰值频率降低。缝隙长度分别为5、10和20mm时，阻尼能的峰值频率出现在140、60和30Hz附近，如图10所示。

仅改变模型中缝隙的大小，发现随着缝隙的增大，阻尼能峰值频率升高。缝隙大小分别为0.03、0.035和0.04mm时，阻尼能的峰值频率出现在40、60和90Hz附近，如图11所示。

通过上述对比可以看出，最大峰值频率与设计参数有关，在设计和匹配张紧器时可以通过改变参数得到所期望的峰值频率。

干摩擦式张紧器的阻尼能基本不随激励频率变化[1]，因此阻尼能可变性也是液压张紧器相对于干摩擦张紧器的一大优点，可以通过合理设计和匹配，使液压张紧器在某阶共振频率附近阻尼能达到最大值，获得最佳减振效果。

5 结论

(1) 建立了考虑油液可压缩性情况下液压张紧器高压腔油压微分方程和单向阀小球运动微分方程，通过对微分方程数值求解，可以得到液压张紧器阻尼力示功曲线、阻尼能和最大阻尼力。

(2) 通过与有限元计算的对比，各频率下阻尼能和最大阻尼力的误差均在5%以下，表明本文中推导的理论模型正确。

(3) 随着激励频率的增大，阻尼能先增大后减小，这是液压张紧器相对于干摩擦式张紧器的一大优点，可以通过合理设计和匹配，使液压张紧器在某阶共振频率附近阻尼能达到最大值，以达到最佳减振效果。

(4) 本文中采用的液压张紧器阻尼特性理论模型的推导方法具有普遍意义，适用于其它液压式自动张紧器阻尼特性的分析计算。

[1] 田力.汽车自动张紧轮设计理论及优化[D].上海:上海大学,2008.

[2] KITANO Satoshi, ANAKA Tadahisa, NAKAGAWA Tomokazu. The Auto-tensioner Market and Technical Trends[J].NTN Technical Review,2005(73):110-117.

[3] Krueger Karin, Engelhardt Thomas, Ginzinger Lucas. Dynamical Analysis of Hydraulic Chain Tensioners-Experiment and Simulation[C]. SAE Paper 2007-01-1461.

[4] Takagishi Hiroshi, Muguruma Kazuto, Takahashi Nobuharu. Analysis of Effect of Tensioner on Chain System[C]. SAE Paper 2008-01-1496.

[5] Manin Lionel, Michon Guilhem, Remond Dither. From Transmission Error Measurement to Pulley-belt Slip Determination in Serpentine Belt Drives: Influence of Tensioner and Belt Characteristics[J]. Mechanism and Machine Theory,2009(44): 813-821.

[6] 刘李平.阀芯阀套间缝隙内部流场的CFD计算[D].太原:太原理工大学,2007.

[7] 袁子荣.液气压传动与控制[M].重庆:重庆大学出版社,2002.

[8] McCloy D, Martin H. Control of Fluid Power : Analysis and Design(2nd edition)[M]. Ellis Horwood Limited,1980.

[9] 张国强,吴家鸣.流体力学[M].北京:机械工业出版社,2005.

[10] 顾宏斌,丁运亮,吴云生,等.油液压缩性对摆振器工作特性的影响[J].南京航空航天大学学报,1999,31(6):656-633.

[11] 冯斌.液压油有效体积弹性模量及测量装置的研究[D].杭州:浙江大学,2011.