THS-III纯电动模式下的发动机转速控制*

赵治国,代显军,王 晨，,张 彤,袁喜悦

(1.同济大学新能源汽车工程中心,上海 201804； 2.浙江吉利罗佑发动机有限公司,宁波 315300)

前言

丰田Prius混合动力汽车最新搭载的THS-III(Toyota hybrid system)系统采用独特的双行星排动力分配和双电机结构，具有纯电动和混合动力两种运行模式。其中，纯电动模式仅利用蓄电池为电机供电驱动车辆行驶，清洁、无污染，多用于城市短途工况。而混合动力模式可以利用电机调速使发动机保持工作在最佳工况区域，提高了整车燃油经济性。

文献[1]中针对THS-II系统，推导了其动力学方程，描述了其能量流动方式，利用杠杆法分析其工作模式，并通过建模仿真验证了基于THS-II系统的整车能量管理策略。文献[2]中对THS系统的电机控制策略进行了研究，为获得较高的电机实际运行效率，分别对其纯电动、混合动力和减速制动模式的双电机的控制方式进行探讨。文献[3]中通过后向仿真，对比分析了THS-II系统和AHS(allison hybrid system)系统的能量分配策略，指出仅有一种功率分流模式的THS-II系统能量损失大于具有两种功率分流模式的AHS系统。文献[4]中推导了THS系统的数学模型，提出了一种改进的基于实时优化的等效燃油消耗量最小控制策略，并通过仿真与实验，证明了其有效性。文献[5]中基于车辆目标运行工况，分析了THS系统各关键动力部件的参数设计要求，并根据蓄电池可用功率，设计并优化了电机控制策略。然而，以上文献对THS-III系统的纯电动模式仅做了稳态研究，并未考虑瞬态过程中的车辆行驶平稳性问题。

本文中以THS-III系统为研究对象，利用杠杆法描述了其纯电动动态加速过程，分析了发动机转速波动的影响因素，针对该过程发动机转速波动会导致其直接被起动的问题，设计了发动机转速补偿控制策略，有效抑制了THS-III系统纯电动模式下发动机转速波动，提高了动力系统的工作效率，改善了车辆行驶的平稳性。

1 THS-III系统杠杆模型

1.1 单行星排杠杆等效

单行星排转矩和转速关系[6]满足方程：

Ts+Tr+Tc=0

(1)

Ts∶Tr∶Tc=1∶i∶-(1+i)

(2)

ws+iwr=(1+i)wc

(3)

式中：Ts、Tr、Tc分别为作用于太阳轮、齿圈、行星架的转矩；ws、wr、wc分别为太阳轮、齿圈、行星架的角速度；i为齿圈与太阳轮的齿数比。根据杠杆法[7-8]，单行星排杠杆等效图如图1所示。

图1中虚线杠杆与s轴、c轴和r轴的交点距水平实线的距离分别代表ws、wc、wr,c轴与r轴、s轴的水平距离代表行星排传动比。

1.2 THS-III系统杠杆等效

丰田汽车公司于2009年推出了Prius第三代车型，它搭载的THS-III混合动力系统如图2所示，采用双行星排、双电机结构，前行星排起功率分流作用，后行星排仅起定轴传动作用。发动机通过扭转减振器与前排行星架相连，小电机MG1(motor and generator)与前排太阳轮相连，大电机MG2(驱动电机)与后排太阳轮相连，后排行星架锁止在变速器壳体上，前后行星排共用齿圈。该变速器为典型的输入功率分流装置，发动机输出功率通过前行星排进行一次分流，分流后的能量一部分通过电机MG1以电能形式作用于电机MG2或者存储于蓄电池中，另一部分以机械能的形式与电机MG2产生的功率复合后传至齿圈输出端。

根据1.1节行星排杠杆等效原理，忽略各元件转动惯量的影响，可以对前行星排进行杠杆等效，如图3所示。

2 纯电动模式下等效杠杆分析

纯电动模式下，电机MG2转矩经后行星排放大在齿圈端产生驱动转矩TMG2，TMG2克服齿圈阻力转矩Tf使齿圈产生角加速度，驱动车辆前行。此外，该合力转矩(TMG2与Tf之差并除去用于使齿圈产生角加速度的转矩)按式(2)在行星架、小太阳轮上产生等效转矩Tc和Ts。若等效转矩Tc小于发动机静态阻力转矩TEng，则发动机转速维持在零点，电机MG1保持空转；反之，若等效转矩Tc大于发动机静态阻力转矩TEng，则发动机将被起动而产生转速波动，由式(3)可知，此时会引起齿圈端转速变化，从而影响输出端平稳性。实际控制应实时调整电机MG1输出转矩TMG1，将行星架转速控制在零点附近，同时为电机MG2提供补偿转矩TMG2′，以消除TMG1对齿圈输出端造成的影响。若纯电动加速过程中行星架转速始终维持在零点，随着车速的增加，齿圈阻力转矩Tf也随之增加，直至电机MG2输出转矩TMG2与齿圈阻力转矩Tf相平衡，杠杆位置保持稳定，系统进入匀速纯电动模式，忽略各个元件转动惯量的影响，纯电动过程等效杠杆如图4所示。

3 发动机转速波动影响因素分析

THS-III系统纯电动模式下只有电机MG2提供驱动转矩时，整车控制框图如图5所示，图中HCU为整车控制器，MCU2为电机MG2控制器，W2、V2、U2为电机MG2的三相电压控制信号。在Matlab软件平台上建立了整车动力系统模型及其在纯电动模式下的控制模型，如图6所示,图中nENG、nMG1、nMG2、nring分别表示仿真过程中发动机、MG1、MG2和齿圈端的转速，TMG1、TMG2表示MG1、MG2的转矩。模型相关部件参数[9]见表1。调整模型参数，仿真对比了THS-III系统纯电动运行时影响发动机转速波动的主要因素，结果分别如图7～图9所示。它们分别为不同的输出端需求转矩、发动机静态阻力矩和扭转减振器阻尼下的齿圈与发动机的转速与转矩时间历程。

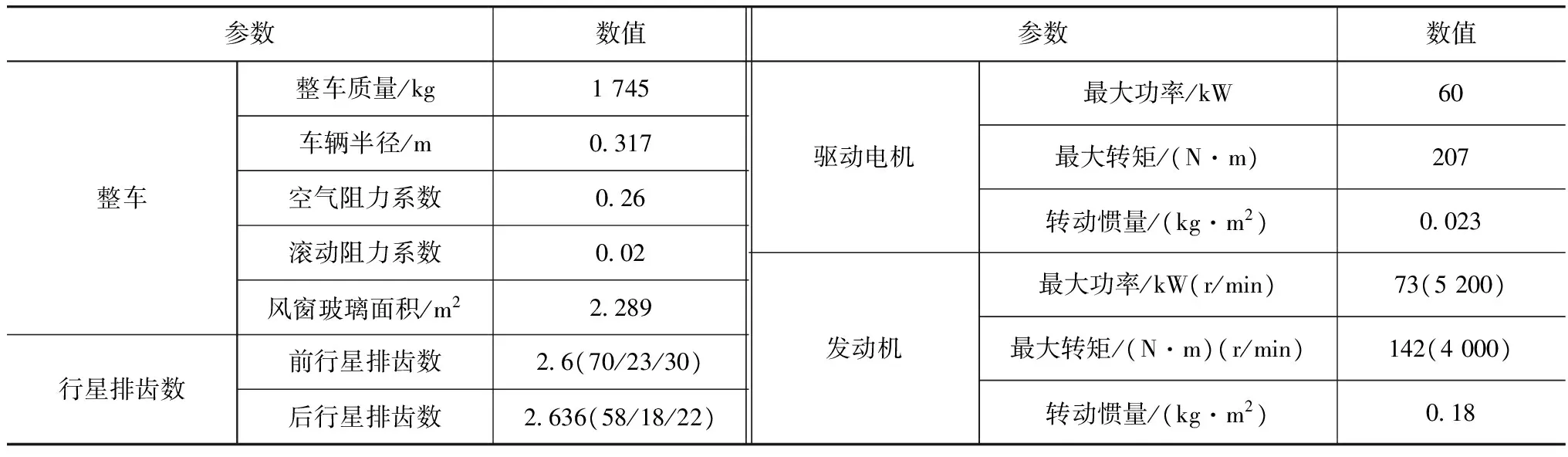
表1 THS-III系统模型主要参数

由图7～图9可见，输出端需求转矩越大，发动机静态阻力转矩越小，扭转减振器阻尼越小，则发动机转速波动越明显，整车行驶平稳性越差。

4 发动机转速补偿控制与仿真

由上述分析可知，若不实施发动机转速补偿控制，THS-III系统纯电动急加速时，发动机会被起动，并产生转速波动，影响了动力输出的平稳性，因此，需要设计发动机转速补偿控制策略抑制其转速波动，以确保整车行驶的平稳性。根据THS-III系统纯电动模式工作原理，并引入发动机转速补偿控制，所设计的整车控制框图如图10所示。

图10中HCU为整车控制器，MCU1为电机MG1的控制器，nENG′为发动机目标控制转速，i为行星排传动比，W1、V1、U1为电机MG1的三相电压控制信号，其余符号的意义同上。

引入的发动机转速补偿控制如图10中点划线框所示，通过控制电机MG1转矩，并进行MG2转矩补偿，将发动机转速控制在零点附近，一方面解决其转速波动所导致的直接被起动的问题，另一方面减少了摩擦功，改善了动力系统的工作效率。

其中PID控制器输入为发动机目标转速(为零)与实际转速之差，输出为电机MG1需求转矩信号。由于发动机转速的采集一般采用霍尔式或磁电式传感器，其采集精度与信号发生频率有关，转速越低，信号采集越不准，而纯电动模式时，发动机被起动的转速往往不高，故送入PID控制器的发动机转速不宜直接用其反馈的转速信号，而应该利用两个电机控制器反馈的电机转速(精度高)通过单行星排转速约束关系计算出发动机转速后送入PID控制器。

电机MG2的需求转矩来源于两部分：一部分是根据输出端工况，根据加速踏板行程和车速信号查整车转矩需求表得到其基本需求转矩，另一部分是添加转矩修正模块，即MG1需求转矩乘以行星排传动比，得到其修正转矩，这两部分叠加后为MG2实际需求转矩。添加MG2转矩修正模块是因为根据式(2)，MG1补偿时其转矩会在齿圈端产生与MG2驱动转矩相反方向的等效转矩，故要添加修正模块以补偿MG1转矩对输出端的影响。

得到电机MG1和MG2的需求转矩信号后，送入电机控制器以控制其转矩输出。为确保动力输出的平稳性，须合理选择整车控制器HCU和电机控制器MCU1、MCU2的采样时间。采样时间越短，电机转矩输出的响应速度越快，能更快地抑制发动机转速波动，进一步改善车辆行驶的平稳性。

纯电动模式下电机MG1、MG2补偿前后的仿真对比结果如图11所示。由图可知，电机MG1、MG2补偿前，发动机转速波动大，持续时间长；补偿后，发动机转速波动减小，并迅速降为零，改善了动力输出的平稳性，从而验证了上述电机补偿策略的有效性。

为分析控制器采样时间对发动机转速波动和动力输出平稳性的影响，在电机补偿作用下，通过设置不同的整车控制器HCU、电机控制器MCU1和MCU2的采样时间(其中较长采样时间为40ms，较短采样时间为10ms)，分别得到不同控制器采样时间下的仿真对比结果，如图12和图13所示。由图12和图13可见，整车控制器HCU和电机控制器MCU1、MCU2采样时间越短，发动机转速和齿圈转矩的波动越小。说明合理选择控制器采样时间，可使PID控制器输出的MG1转矩和齿圈端的MG2转矩均能更快地抑制发动机转速波动和补偿输出，从而改善动力输出的平稳性。

最终引入发动机转速补偿控制并合理选择控制器采样时间(控制器HCU、MCU1、MCU2采样时间均为0.01s)，得到的仿真结果如图14所示。可见优化后发动机转速波动范围小，持续时间短，并迅速下降为零，齿圈转矩波动也较小，输出端平稳性得到明显改善。至此，THS-III系统纯电动整车控制策略的有效性得到验证。

5 结论

(1) 利用杠杆法对THS-III系统纯电动加速过程进行的分析表明：纯电动模式下若仅对电机MG2实施转矩控制，可能会直接导致发动机被起动，不仅严重影响车辆行驶的平稳性，而且会降低系统的工作效率。

(2) 输出端需求转矩、发动机静态阻力转矩和扭转减振器阻尼是影响发动机转速波动的主要因素。输出端需求转矩越大，发动机静态阻力转矩越小，扭转减振器阻尼越小，则发动机转速波动越明显。

(3) 发动机转速补偿控制能够明显降低其转速波动范围，并且通过电机MG2转矩补偿，能够确保动力输出端的转矩响应和控制精度。同时，合理选择采样时间也能明显改善车辆的行驶平稳性。

[1] Mansour C, Clodic D. Dynamic Modeling of the Electro-mechanical Configuration of the Toyota Hybrid System Series/parallel Power Train[J]. International Journal of Automotive Technology,2012,13(1):143-166.

[2] Kim J, Kim N, Hwang S, et al. Motor Control of Input-split Hybrid Electric Vehicles[J]. International Journal of Automotive Technology,2009,10(6):733-742.

[3] John Arata, Michael J Leamy, Jerome Meisel, et al. Backward-Looking Simulation of the Toyota Prius and General Motors Two-Mode Power-Split HEV Powertrains[C]. SAE Paper 2011-01-0948.

[4] Liu Jinming, Peng Huei. Control Optimization for a Power-Split Hybrid Vehicle[C]. Proceedings of the 2006 American Control Conference Minneapolies, Minnesota, USA, June 14-16,2006.

[5] Akihiro Kimura, Tetsuya Abe, Shoichi Sasaki. Drive Force Control of a Parallel-series Hybrid System[J]. JSAE Review,1999,20:337-341.

[6] 葛安林.车辆自动变速器理论与设计[M].北京:机械工业出版社,1991.

[7] 冯樱.运用杠杆法计算汽车行星齿轮变速器的传动[J].湖北汽车工业学院学报,2008,22(3):17-20.

[8] Bendord H, Leising M. The Lever Analogy:a New Tool in Transmission Analysis[C]. SAE Paper 810102.

[9] U.S. Department of Energy Vehicle Technologies. Evaluations of the 2010 Toyota Prius Hybrid Synergy Drive System20585-0121[R]. Oak Ridge Natioanal Laboratory Mitch Olszewski,2011.