六轮电驱动铰接式自卸车操纵稳定性研究*
张学艳,张文明,罗维东,黄夏旭
(1.北京联合大学机电学院,北京 100020; 2.北京科技大学机械工程学院,北京 100083)
前言
铰接式车辆不同于单体车辆,由于铰接体和转向系统的作用,前后车体间存在附加的自由度,致使铰接式车辆行驶稳定性差,高速行驶时容易出现“蛇形”失稳现象,因此很多文献对铰接式车辆直线行驶稳定性进行了研究[1-4],但这些研究中所建的模型都没有考虑车体侧倾自由度,而建立动力学模型的研究就更少。
本文中以60t六轮电驱动铰接式自卸车(articulated dump truck, ADT)为研究对象,建立考虑车体侧倾自由度的转向数学模型,研究结构参数对车辆稳定性的影响;并在ADAMS中建立整车的多体动力学模型,在AMESim中建立整车转向系统和液压悬架系统模型,通过ADAMS/AMESim联合仿真进一步分析整车和结构参数对操纵稳定性的影响。
1 车体转向数学模型
本文中应用相对坐标系的动力学方程建立铰接式自卸车的转向运动模型[5]。在转向工况的操纵稳定性分析中,汽车沿相对坐标系Z轴方向的平动与绕Y轴方向的转动相对很小,因此忽略这两个方向的运动。图1为60t ADT车体速度、受力和加速度分析图(顶视图)。
图1中,坐标系O′X′Y′Z′是固定在地面上的绝对坐标系,X′、Y′轴在纸面内,Z′轴指向外;OXYZ是坐标原点固定在前车体质心位置上的动坐标系,且X轴与前车体纵向轴线重合;O″X″Y″Z″是坐标原点固定在后车体质心位置上的动坐标系,X″轴与后车体纵向轴线重合;δ为前后车体间的夹角;B为前后车体轮距的一半;Lf为前轴中点到铰接点的距离;Lr1为中轮中心到铰接点的距离;Lr2为后轴中点到铰接点在地面的投影距离;hf为前车体质心到铰接点的距离;hr为后车体质心到铰接点的距离。u1、v1、r1分别为前车体质心处的纵向速度、横向速度和绕Z轴的横摆角速度;u2、v2、r2分别为后车体质心处的纵向速度、横向速度和绕Z″轴的横摆角速度;a1x、a1y分别为前车体质心处沿X轴和Y轴的加速度;a2x、a2y分别为后车体质心处沿X″轴和Y″轴的加速度;Fix、Fiy分别为地面对i(i=1~6)号车轮的切向力和侧向力;T0为前后车体间的转向内力矩;Fx、Fy分别为铰接点沿X轴和Y轴的相互作用力。
60t ADT前车体采用单纵臂式油气独立悬架,前车体的侧倾中心O位于前车体纵向对称平面与地平面的交线上[6-7],如图2所示。图中:φ为前车体簧上质量的侧倾角(侧倾角速度为p);h1为簧上质量ms1的质心到侧倾中心的距离(侧倾力臂);hj为铰接点到侧倾中心的垂向距离。60t ADT后悬架没有设置弹性阻尼元件,因此不考虑后车体簧载质量的侧倾运动。
1.1 车体运动方程
为简化分析,对铰接式自卸车做如下假设:(1)车辆在水平面上运动,不考虑地面不平度的影响;(2)忽略空气阻力;(3)因车轮回正力矩作用微小,故忽略车轮回正力矩的影响;(4)忽略旋转零件的陀螺效应;(5)忽略对运动影响不大的摩擦力,如前后车体铰接处的摩擦力矩等。
根据相对坐标系的动力学方程,在动坐标系OXYZ中沿X轴、Y轴的受力平衡,得
(1)
(2)
绕X轴、Z轴的力矩平衡,得
-Dp-(Cφ-ms1h1g)φ-Fyhj
(3)
(F1y+F2y)(hf-Lf)-Fyhf
(4)
式中:m1为前车体质量;IXX为前车体簧上质量绕X轴的惯性矩;IXZ为簧上质量对X轴与Z轴的惯性积;D为悬架阻尼;Cφ为悬架刚度;ms1为簧上质量;IZZ1为前车体总质量绕Z轴的转动惯量。
在动坐标系O″X″Y″Z″中沿X″轴、Y″轴的受力平衡,得
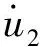
(5)
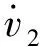
(6)
绕Z轴的力矩平衡,得
(F5y+F6y)(Lr2-hr)+(Fycosδ-Fxsinδ)hr
(7)
式中:m2为后车体质量;IZZ2为后车体总质量绕Z″轴的转动惯量。
根据坐标变换可得前后车体的速度和加速度的关系为
(8)
(9)
联立式(1)~式(9)可得系统动力学微分方程组。当整车进行小角度转向时,侧向加速度较小,轮胎侧偏特性处于线性范围,可忽略轮距影响,各轮侧偏角取为车轴中点处的侧偏角;忽略左右轮纵向力的差别,根据文献[7],忽略空气阻力,水平路面匀速行驶的全轮驱动车辆纵向力之和约等于零;由于中后轮轴距较短且有平衡梁结构,因此后四轮侧偏刚度取相同。则前述转向模型可简化为车轴模型。
1.1.1 轮胎侧偏力
Fiy=kiβi(i=1~6)
(10)
式中:ki为i号轮胎的侧偏刚度;βi为i号轮胎的侧偏角。
1.1.2 转向力矩
前、后车架和转向油缸的三维图如图3所示。前后车架通过铰接体连接,前车架以铰接体的上下两个铰点为中心相对后车架可在横向平面内转动,转向油缸绕铰接点动作实现前后车体的相对转动,从而完成转向功能。转向油缸简图如图4所示。
图4中,O为铰接点,A和D为转向杆与铰接体的连接点(横向平面内铰接体与后车架没有相对自由度,即此时A和D相当于转向杆与后车架的连接点),B和C为转向缸与前车架的连接点,B′和C′为前后车体转过δ角后转向缸与前车架的连接点,A1为转向缸无杆腔截面积,A2为转向缸有杆腔截面积,p1为转向缸进油腔压力,p2为转向缸回油腔压力,φ0为转向缸初始安装角度,h1、h2分别为左右转向缸的作用力臂。
当整车转向时,液压缸提供的转向力矩等于左右转向缸力矩之和:
T0=(p1A1-p2A2)h1+(p1A2-p2A1)h2
(11)
设转向盘输入角造成的前后车体的折转角为δN,由于油液可压缩性和传动机构的弹性等,车体实际折转角δ与δN间存在微小增量[8]。根据可压缩性流体流量连续性方程,稳态转向的转向力矩[9]为
T0=-kcy(δ-δN)
(12)
此时液压转向系统可等效为一个作用于铰接点,连接前后车体的扭转弹簧,其刚度为
(13)
式中:V1、V2分别为油缸进、出油端体积;βe为有效液体体积弹性模数。
1.2 稳定行驶
(14)
其中:
X=[v1r1r2pδφ]T
F=[0kcyδNkcyδN0 0 0]T
1.2.1 稳定行驶条件

BX=F
(15)
根据Hurwitz稳定性判断依据,式(15)存在稳定响应的条件是det(B)>0。将B的行列式展开得:
(16)
(17)
K为ADT行驶的稳定性因数,式(17)中,kf=2k1,kr=4k3,2Lr=Lr1+Lr2。则60t ADT稳定行驶的条件为:(1)Cφ-ms1h1g>0;(2)1+Ku12>0。
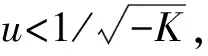
由ADT稳定行驶条件可知,考虑了侧倾自由度的铰接式自卸车的行驶稳定性不但要满足稳定性因数的要求,侧倾角刚度也要大于簧载质量重力与侧倾力臂的乘积。
根据60t ADT的结构参数,见表1,计算得满载稳定性因数K=0.001 6,特征车速uch=25.2m/s,空载稳定性因数K=0.001 8,特征车速uch=23.5m/s,该车具有不足转向特性。
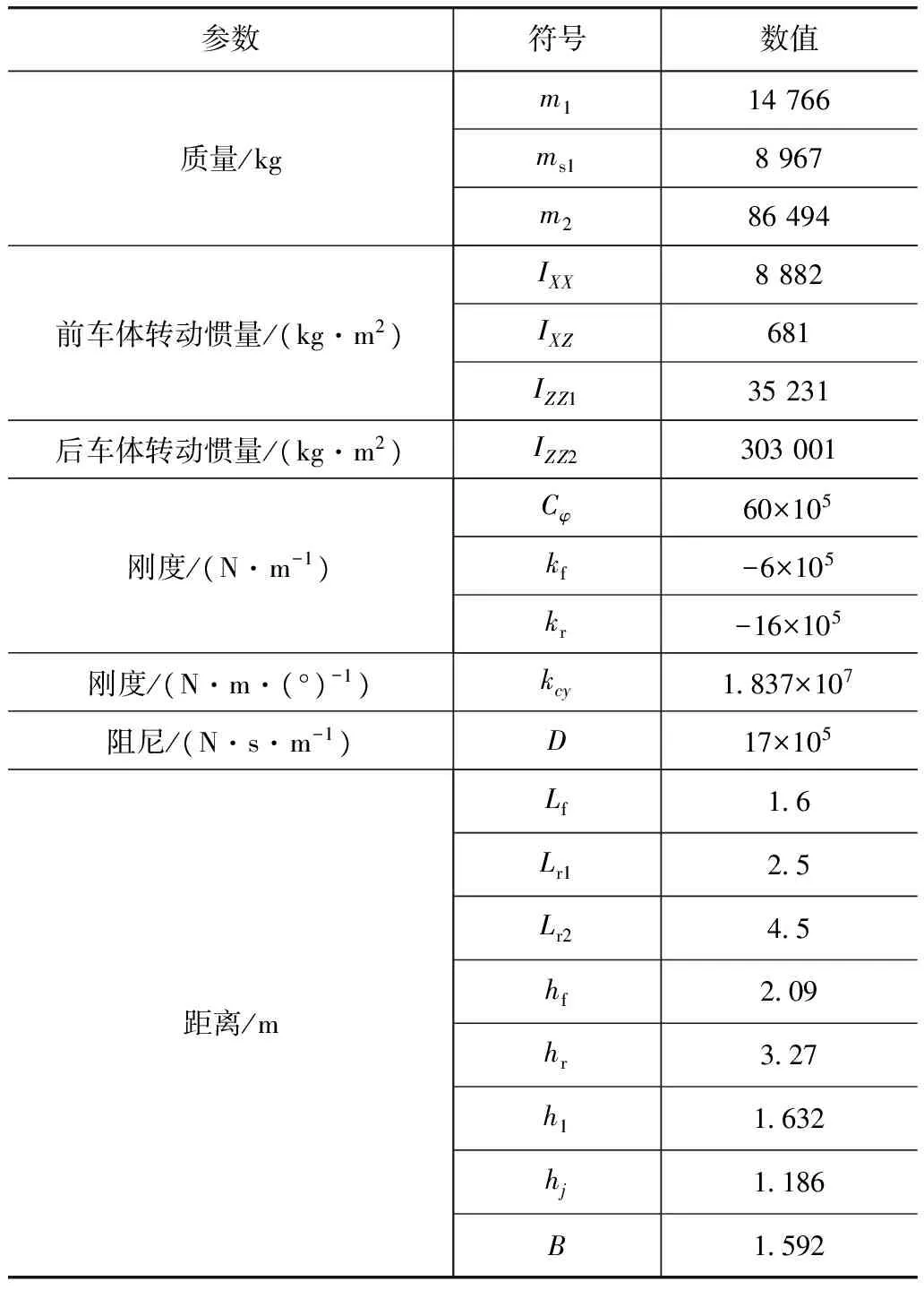
表1 铰接车结构参数
1.2.2 结构参数对稳定行驶的影响
铰接式自卸车由于驾驶室、水箱、燃油箱等的位置,前车体质心位置会发生变化;后车体由于货物的堆装质心位置也会变动[11]。
将Lf按前后桥距离L的0、20%、40%、60%变化,hf与Lf的比值δf按0.2、0.4、0.6、0.8、1、1.2变化,hr与Lr的比值δr按0.2、0.4、0.6、0.8、1、1.2变化,则稳定性因数随Lf和hf、Lr和hr的变化趋势如图5和图6所示。
由图5可见,当hr=0.8Lr时,随着Lf的增大,稳定性因数呈减小趋势,当Lf=0时,铰接式自卸车即转化为单体车,稳定性因数达到最大。当hr=1.2Lr时,无论Lf和δf如何增减,稳定性因数都是负值。
由图6可见,hf=0.8Lf和hf=1.2Lf对稳定性因数均影响不大,即图5中,对Lf的某一固定值,不同δf对稳定性因数的影响不大。由图6可以看出,当δr<1时,无论后轮轴线到铰接点距离增大还是减小,稳定性因数K均大于零;但当δr=1.2时,无论后轮轴线到铰接点距离增大还是减小,稳定性因数K均小于零,即铰接式自卸车具有过多转向特性,这与图5的结论是吻合的。
由以上分析可知,Lf、hf对整车的行驶稳定性影响不大,hr与Lr的比值δr对稳定性影响显著,为保证铰接式自卸车具有适度不足转向的特性,δr只能在1附近微幅变动。
2 整车操纵稳定性联合仿真分析
60t ADT的主要部件包括:前后车架、铰接体、悬架系统、发动机、货箱、轮胎等。根据整车结构设计图纸,在三维建模软件SolidWorks中建立各零部件并装配。
将SolidWorks中的整车模型导入ADAMS/View中,通过设置各零部件的材料属性,添加零部件的约束及力的关系,得到了ADAMS中整车多体仿真模型,如图7所示。
整车模型中各部件之间在ADAMS/View中的约束和连接关系如图8所示,图中R表示旋转副,F表示固定副,S表示球铰副。整车中除油气弹簧外,其它弹性元件采用轴套力(bushing)模拟,如驾驶室与前车架的减振垫和货箱与后车架的减振垫。
整车多体动力学模型中,轮胎选用UA轮胎模型,其特点是各方向的力和力矩由耦合的侧偏角、滑移率、外倾角和垂向变形等参数显式表达。该模型考虑了纵向和侧向联合滑动的工况,因而准确、全面[12]。轮胎特性参数如表2所示。
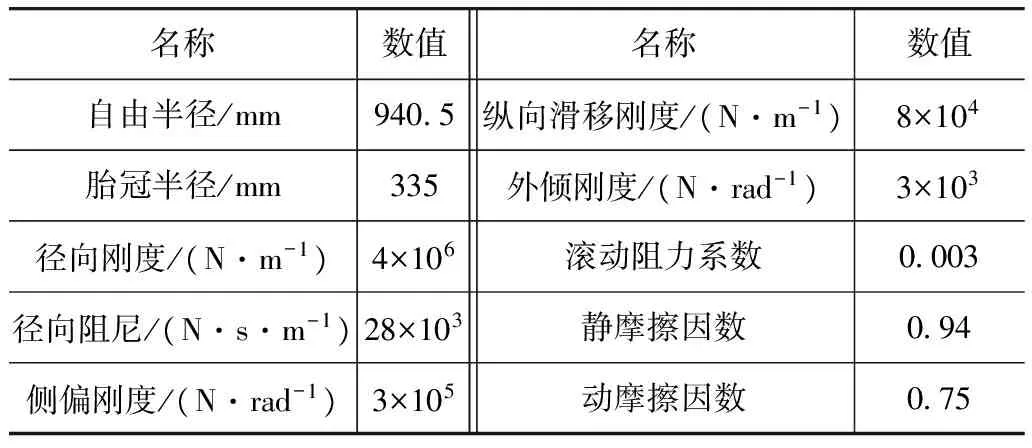
表2 轮胎特性参数
为了更准确地建立整车模型,在AMESim液压仿真平台上建立全液压转向系统和油气弹簧的液压模型[13]。60t ADT采用的是摆线转阀式全液压转向器,根据转向器的工作原理,以车体折转角与转向盘输入角的关系作为外部反馈模拟转向器阀芯与阀套的内部反馈,从而控制转向器的进出油量,节流口用以模拟转向器中阀芯阀套形成的配油面积[14-15],如图9所示。根据单气室油气弹簧结构特点,在AMESim中,通过缸筒外接一个蓄能器及两个阻尼孔和单向阀搭建单气室油气弹簧的液压模型,其部分参数如表3所示。
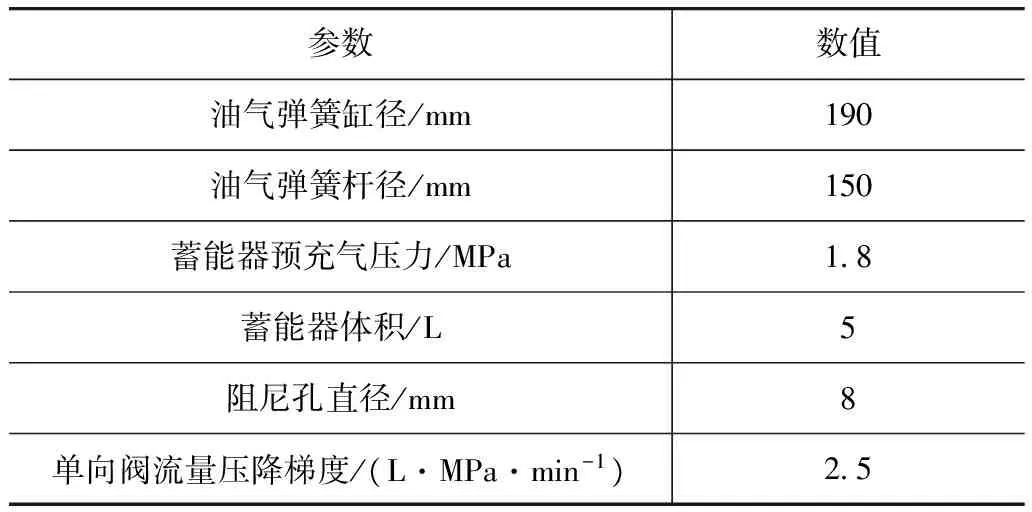
表3 单气室油气弹簧参数
联合仿真采用以AMESim仿真平台为主,将ADAMS模型编译后成为AMESim识别的模块插入AMESim模型中[16],如图9所示。
联合仿真模型创建过程为:(1)在ADAMS中创建状态变量,包括油气弹簧油缸和活塞杆间相对位移、相对速度和油气弹簧输出作用力,左右液压转向缸筒和转向杆间的相对位移、相对速度和油缸输出力,前后车架间的折转角,并将油气弹簧作用力、左右转向缸作用力定义为控制输入,将油气弹簧和转向系统的相对位移、相对速度和前后车架的折转角定义为控制输出;(2)AMESim中导入ADAMS-TO-AMESim模块,ADAMS中输出的位移、速度、加速度和折转角等信号传给AMESim,AMESim中油气弹簧根据其输入位移和速度计算其输出力,液压转向系统将ADAMS输出的折转角信号与转向输入信号进行比较,控制转向系统节流口的开度,从而输出转向缸的作用力,这些力信号输入到ADAMS-TO-AMESim模块中,传输给ADAMS。这样,两个软件通过联合仿真实现数据的相互交换。
图9中,glf、grf分别代表左、右侧转向缸的输出力;glx、glv分别代表左侧液压转向缸筒和转向杆间的相对位移、相对速度;grx、grv分别代表右侧液压转向缸筒和转向杆间的相对位移、相对速度;flf、frf分别代表左前、右前油气弹簧活塞杆的输出力;flx、flv分别代表左前油气弹簧油缸和活塞杆间相对位移、相对速度;frx、frv分别代表右前油气弹簧油缸和活塞杆间相对位移、相对速度;zhezhuanjiao代表前后车架的折转角。
2.1 稳态回转试验
采用固定转向盘转角连续加速方法对铰接式自卸车进行水平路面的稳态回转试验。前后车体折转角见图10,整车稳态回转运动轨迹如图11所示。
由图11可以看出,该铰接式自卸车具有不足转向特性,与数学模型结论一致。
2.2 质心位置对操纵稳定性的影响
不同车速下,后车体质心分别向前和向后移动200和300mm,对整车进行转向盘角阶跃输入试验,前车体横摆角速度、侧向加速度和侧倾角随时间的变化曲线如图12~图14所示。
由图12和图13可以看出,在低速时,后车体质心位置变化对横摆角速度和侧向加速度影响不大,随车速提高和质心位置后移量的增加,横摆角速度和侧向加速度越来越大。
图14中侧倾角随后车体质心位置变化的响应比较复杂。当车速较低时,如图14(a)所示,前移后车体质心增大侧倾角,后移质心时,出现侧倾方向相反的情况。这是由铰接车前后车体的特殊结构决定的。对于铰接式车辆,当车体静止且前后车体存在一个固定折转角时,路面对前轮内轮的垂向载荷大于外轮的垂向载荷,此时前车体向内侧方向倾斜(设此时侧倾角为正值);后移后车体质心位置会增大内轮垂向载荷与外轮垂向载荷的差值,即侧倾角变大;前移后车体质心则侧倾角变小,甚至变为负值。在车速较低时,离心力对侧倾角的影响较小,即主要是后车体质心位置对侧倾角的影响,因此前移或后移车体质心位置使侧倾角出现正负相反的情况。由图14(b)可知,当车速达到20km/h时,侧倾角都为负,离心力开始起作用,使外轮垂向载荷变大,车体向外侧倾斜,侧倾角都变为负值。图14(c)和图14(d)的趋势与图14(b)的趋势相反,后移车体质心增大了车体侧倾角,说明在车速较高的情况下,由于车体质心后移使侧向加速变大,在离心力的作用下侧倾角变大。综上所述,适当后移车体质心,车辆在中低车速行驶时,有利于降低车体侧倾角,高速行驶时不利于降低车体侧倾角。由于转弯工况时车辆大都低速行驶,因此可以考虑后移车体质心以减小车体侧倾。
后移后车体质心会影响车体的转弯半径,如图15所示。
由图15可见,相同车速下,后移车体质心减小转弯半径,不足转向量降低,这与图6的结论一致。
3 结论
(1) 建立了考虑车体侧倾自由度的铰接式自卸车转向运动数学模型,得到时不变输入下稳定行驶的条件:侧倾角刚度要大于簧载质量重力与侧倾力臂的乘积;稳定性因数大于零或稳定性因数小于零时,车速小于临界车速。分析了结构参数对行驶稳定性的影响,得出为保证铰接式自卸车具有适度不足转向的特性,应使后车体质心在后桥中心附近微幅变动。
(2) 利用ADAMS建立整车多体动力学模型,利用AMESim建立全液压转向系统和油气弹簧的液压模型,通过ADAMS/AMESim联合仿真分析整车操纵稳定性和车体质心位置变化对操纵稳定性的影响。结果表明:适当后移车体质心,车辆在中低车速行驶时,有利于降低车体侧倾角,高速行驶时不利于降低车体侧倾角;后移车体质心会减小转弯半径,不足转向量降低。仿真结果验证了数学模型的正确性。
[1] 葛强胜.铰接式车辆高速直线行驶动态仿真[J].农业机械学报,2003,34(4):39-42.
[2] 刘刚,张子达,邹广德,等.铰接车辆行驶稳定性的动力学建模[J].工程机械,1996(8):5-8.
[3] 汪建春,杨文华.铰接式装载机直线行驶稳定性分析[J].矿山机械,1996(2):2-6.
[4] Azad N L. Dynamic Modelling and Stability Controller Development for Articulated Steer Vehicles[D]. University of Waterloo,2006.
[5] 郑军.新概念车舒适性与操纵稳定性研究[D].长沙:湖南大学,2001.
[6] 刘惟信.汽车设计[M].北京:清华大学出版社,2001.
[7] Manfred Mitschke, Henning Wallentowitz.汽车动力学[M].陈荫三,余强,译.北京:清华大学出版社,2009.
[8] 刘刚.铰接车辆行驶动态特性的研究[D].长春:吉林工业大学,1997.
[9] 汪建春.铰接式车辆液压转向系统当量扭转刚度讨论[J].矿山机械,2008(7):47-49.
[10] 刘刚,张子达.铰接式车辆行驶稳定性的理论分析与数值计算[J].吉林大学学报(工学版),2004,34(3):367-372.
[11] 刘晋霞.非公路运输车辆操纵稳定性研究[D].北京:北京科技大学,2006.
[12] 冯金芝,喻凡,李君.基于虚拟样机技术的铰接式车辆动力学建模[J].上海理工大学学报,2004(4):372-377.
[13] Yanhua S, Taohua Z, Chun J. Co-simulation Analysis of Zero Radius Steering Characteristics of Articulated Vehicle with Six Motor-driven Wheels[C]. Electric Information and Control Engineering (ICEICE),2011:4848-4851.
[14] 侯友山.铰接车辆转向液压系统关键技术研究[D].北京:北京科技大学,2010.
[15] 王辉.矿用汽车前桥及转向机构的设计研究[D].北京:北京科技大学,2012.
[16] 杜恒,魏建华.基于遗传算法的连通式油气悬架平顺性与道路友好性参数优化[J].振动与冲击,2011(8):133-138.

