成品粮应急代储系统发展对策研究

胡会琴，侯云先，安久意

(1.中国农业大学经济与管理学院，北京 100083;2.北京物资学院物流学院，北京 101149)

一、引 言

进入21世纪以来，全球经济环境与自然环境遭遇着前所未有的挑战。全球金融危机对国内外粮食市场的供求格局和粮价走势产生了深刻影响，粮食加工业的市场风险迅速增加。同时，各类突发公共事件也更加频繁，这使得各国政府都更加重视和支持粮食储备。［1］我国粮食储备系统的公共服务能力也受到了严峻挑战，尤其是能够快速转化为食品的成品粮应急储备，成为考验各级政府应急减灾能力的重要指标之一。我国在经历了2003年“非典”、2008年汶川地震等重大突发事件之后，才逐步开始重视成品粮应急储备建设。成品粮应急储备系统是由地方政府、成品粮应急代储企业和供应网点构成的复杂政治、经济综合体，代储企业和供应网点的各种投机行为时有发生，严重危及到民众的公共利益。如2011年，中储粮未经内部审批在北京农村商业银行等13家商业银行开立定期存单，累计资金84.4亿元①，诸如此类既拿政府补贴又入市牟利的案例在实际工作中屡见不鲜。本文将运用博弈链理论与方法对成品粮应急代储系统中“政府—代储企业—供应网点”之间的博弈行为进行分析，为促进成品粮应急代储系统的发展提供决策依据。

博弈链理论基于系统思维方式，从全新的视角揭示组织系统复杂的博弈关系及演化规律。［2］与传统的博弈思想相比，博弈链将多个博弈主体视为一个整体，能够更好地研究实际问题中多个博弈主体间的相互影响，是研究多主体合作问题的重要工具。［3］［4］如在分析军民两用高技术产业集群核心企业与一级分包商，以及分包商与二级分包商两阶段知识博弈链模型均衡解的基础上，提出了产业集群协同创新机理;［5］通过对产学研合作中两个随机主体的博弈研究整个群体的进化规律，以及不同进化阶段的均衡状态，以促进区域产学研合作，［6］与之相似的还有产品研发设计链中知识共享机制的构建［7］。

三方博弈在现实生活中也较常见，如在大型灾害应急救援过程中，中央政府的投入及惩罚决定了地方政府的投入，而中央政府和地方政府的投入又决定了灾民的努力程度，对此三方博弈均衡状态的分析可为改进应急救援效率提供一些建议。［8］劳资关系也一直是社会关注的重要问题，政府、企业和劳工间的博弈及合约选择行为形成了“均衡陷阱”，定性分析三方均衡可从中得出跳出陷阱的策略。［9］另外，随着信息技术的发展，网络舆情对社会各方面的影响越来越大，而网络推手是网络舆情演化过程中的重要因素，通过对网络推手问题中的当事人、网络推手和政府间的三方博弈局势及复制动态方程进行分析，可为政府监管，以及当事人和网络推手合作等问题提出相应的应对策略。［10］可见，目前博弈链理论与方法多应用于两个主体间的博弈均衡研究，而三方博弈多以定性分析或三主体为一个博弈局势进行研究。本文将博弈链思想与一般的三方博弈方法相结合，通过一定的传递机制，将“地方政府—代储企业—供应网点”三个主体间的多个博弈局势联系起来，以系统为着眼点，由部分到整体，更深入系统地研究成品粮应急代储系统的演化规律。

二、成品粮应急代储系统博弈关系的形成机理

1.成品粮应急代储系统的界定

我国粮食储备体系实行垂直管理模式，由中央储备粮和地方储备粮构成。中央储备粮主要是原粮，由中国储备粮管理总公司和部分代储企业进行储备;地方储备粮实行省长负责制，储粮结构逐步调整为“原粮+成品粮”，其中成品粮一般由具有代储资格的当地企业进行承储。从储备功能看，粮食储备主要包括战略储备、后备储备和周转储备(商品储备)。［11］其中，后备储备以平抑粮食价格与调节粮食供需平衡为基本目的，是应对市场波动和突发事件的重要物资储备，直接决定着一个国家或地区的粮食安全，是各国都非常重视的一种储备。而终端供应则由具有一定资质的供应网点完成。［12］

本文所研究的成品粮应急代储系统(简称“代储系统”)是指在地方政府的主导下，由代储企业承储一定数量和品质的大米和(或)小麦粉，并在突发事件发生后将成品粮配送至其服务的供应网点，由供应网点完成终端供应，以实现平抑粮食市场价格波动或满足各类公共突发事件应急需求的政治、经济综合体。

2.成品粮应急代储系统的结构和主体行为

我国成品粮应急代储系统已基本形成，在近年的重大公共突发事件救援中发挥了重大作用。该系统中各要素之间，以及与经济、政治、文化等外界环境之间相互作用、相互影响。因此，可将成品粮应急代储系统视为一个由“地方政府—代储企业—供应网点”构成的三级供应保障网络。

(1)地方政府与代储企业间的结构关系。与原粮相比，成品粮轮换频次更高、风险更大，基于成本和效益两方面的考虑，地方政府一般利用当地符合代储资格的企业进行承储，以低成本实现应急保障的高效益。地方政府给予代储企业一定的财政补贴，并对其保管、轮换和配送等活动进行监管。因此，代储企业对地方政府的行为选择为努力或不努力，其收益主要来自地方政府的补贴、轮换盈余收益和投机收益等。

(2)地方政府与供应网点间的结构关系。健全的粮食供应网络是应急时期政府与民众及时衔接、准确投放的保障。供应网点多以当地的大型商超、粮油批发市场、便利店等商贸企业为主。地方政府对供应网点的应急保供工作进行监管，并给予一定的财政补贴。供应网点对政府的行为选择为努力或不努力，其收益主要来自于政府补贴、销售价差以及投机收益。

(3)代储企业与供应网点间的结构关系。地方政府对成品粮应急储备实行“政府委托、逐级负责、部门监管、企业运作”的管理办法。代储企业和供应网点接受政府委托，分别履行仓储配送和终端供应的职责，共同构成成品粮应急储备和应急供应网络。地方政府根据代储企业的承储规模和位置确定其最佳服务的供应网点数量和范围，应急时代储企业将一定数量和规格的成品粮配送至其服务的供应网点，供应网点在政府指导和监管下完成供应任务。代储企业与供应网点相互的行为选择为串谋或不串谋。在整个博弈过程中，地方政府的行为选择为对代储企业和供应网点进行监管或不监管，其收益主要包括上级拨款和为保证应急成品粮供应、维护社会稳定等所发生的无形可估算成本，以及监管时发现代储企业和供应网点不合法或不作为等举动的罚款收益。

三、成品粮应急代储系统博弈链模型

1.基本假设

在代储过程中，地方政府不能直接观察到代储企业和供应网点的努力程度，且代储企业和供应网点都是追求利益最大化的。故此，本模型作如下假设:

(1)参与人:地方政府、代储企业、供应网点。

(2)参与人三方是信息不对称的，且都是风险中性的有限理性经济人。

(3)博弈结构:地方政府和代储企业之间为博弈Ⅰ，与供应网点之间为博弈Ⅱ，代储企业和供应网点之间为博弈Ⅲ。

(4)地方政府对代储企业和供应网点的策略集合为(监管，不监管)，监管概率为ps∈［0，1］。只要政府监管，就能发现代储企业和供应网点的串谋行为。

(5)代储企业和供应网点的串谋概率为p1∈［0，1］，串谋总收益为Tc，二者的串谋收益分别为∂tc(0＜∂＜1)和(1－∂)tc。若串谋行为被地方政府发现，串谋收益不仅被没收，还将受到与串谋收益成正比的罚款，分别为 a1Tc和 a2Tc(a1，a2＞0)。

(6)代储企业和供应网点的策略集合为(串谋，不串谋)。

2.成品粮应急代储系统博弈链模型的构建

(1)博弈Ⅰ:地方政府与代储企业间的博弈

我国成品粮应急储备实行定额包干制，地方政府对代储企业i的财政补贴为R1i=r1Q1i(r1为单位成品粮补贴额，Q1i为代储企业的承储量)，代储企业则要自负轮换盈亏L1i，以及成品粮采购成本、贷款利息、仓储成本、轮换成本、人工成本和管理成本等必需成本C1i。因此，代储企业不串谋时的收益为R1i+L1i－C1i。当代储企业采取串谋策略时，其投机收益为∂Tc，一旦被地方政府发现，将受到a1Tc的罚款，则在政府监管情况下的串谋收益为R1i+L1i－C1i－a1Tc;若不被政府发现，其收益为R1i+L1i－C1i+∂Tc。因此，代储企业在不串谋和串谋两种情况下的收益分别为R1i+L1i－C1i和R1i+L1i－C1i+∂Tc(或R1i+L1i－C1i－a1Tc)。

在此过程中，地方政府的收益为Rg1。若对代储企业进行监管，就要付出相应的监管成本Cr1，此时若代储企业进行串谋，则地方政府可获得a1Tc+a2Tc的罚款收益;若代储企业不串谋，则其收益为Rg1－Cr1;若地方政府不监管，不发生监管成本也没有额外收益。因此，地方政府进行监管和不监管时的收益分别为Rg1－Cr1(或Rg1－Cr1+a1Tc+a2Tc)和Rg1。则地方政府与代储企业的收益矩阵如表1所示。

表1 成品粮应急代储系统博弈Ⅰ的收益矩阵

①基于代储企业在串谋和不串谋两种策略下的收益情况可知，代储企业的期望收益为p1［ps(R1i+L1i－C1i－a1Tc)+(1－ps)(R1i+L1i－C1i+∂Tc)］+(1－p1)(R1i+L1i－C1i)，即(R1i+L1i－C1i)+((1－ps)∂－a1ps)p1Tc。显然，代储企业是否投机，与其自身的串谋收益，以及政府的监管概率和惩罚力度有关。只有当((1－ps)∂－a1ps)p1Tc＜0，即代储企业的串谋收益小于地方政府的罚款时，代储企业才不会与供应网点串谋;否则，代储企业的最佳策略为串谋。

②地方政府的期望收益为ps［p1(Rg1－Cr1+a1Tc+a2Tc)+(1－p1)(Rg1－Cr1)］+(1－ps)Rg1，即Rg1+ps(p1(a1+a2)Tc－Cr1)。可知，只有当ps(p1(a1+a2)Tc－Cr1)＞0时，即罚款收益大于监管成本时，地方政府才会进行监管，此时的纳什均衡为(监管，不串谋);当ps(p1(a1+a2)Tc－Cr1)＜0，即监管成本大于罚款收益时，地方政府的最佳策略为不监管，此时的纳什均衡为(不监管，串谋)。

(2)博弈Ⅱ:地方政府与供应网点间的博弈

地方政府对供应网点的补贴为R2j=r2Q2j(r2为供应单位成品粮的补贴额，Q2j为供应网点j的供应量)，供应网点可以从成品粮销售差价中获益S2j，同时，也要消耗采购成本、短暂的仓储成本、人工成本和管理成本等必需成本C2j。

供应网点若不串谋，无论地方政府是否监管，其收益均为R2j+S2j－C2j。若供应网点与代储企业串谋，其串谋收益为(1－∂)Tc，在政府不监管的情况下，其收益为R2j+S2j－C2j+(1－∂)Tc;若政府监管，其收益为R2j+S2j－C2j－a2Tc。则供应网点在不串谋和串谋两种策略下的收益分别为R2j+S2j和R2j+S2j－C2j－a2Tc(或 R2j+S2j－C2j+(1－∂)Tc)。

地方政府对供应网点可采取监管和不监管两种策略，此时其收益为Rg2。若进行监管，成本为Cr2，发现供应网点的串谋行为可获得a1Tc+a2Tc的罚款收益，但供应网点也可能不串谋，地方政府就没有额外收益;若不进行监管，则没有监管成本，也没有罚款收益。因此，地方政府对供应网点监管和不监管时的收益分别为Rg2－Cr2+a2Tc(或Rg2－Cr2)和Rg2。则二者的收益矩阵如表2所示。

表2 成品粮应急代储系统博弈Ⅱ的收益矩阵

①由表2可知，供应网点的期望收益为p1［ps(R2j+S2j－C2j－a2Tc)+(1－ps)(R2j+S2j－C2j+(1－∂)Tc)］+(1－p1)(R2j+S2j－C2j)，即R2j+S2j－C2j+((1－ps)(1－∂)－a2ps)p1Tc。可知，只有当((1－ps)(1－∂)－a2ps)p1Tc＞0，即供应网点的串谋期望收益大于政府罚款时，供应网点才会选择串谋。否则，供应网点便不会串谋。

②地方政府的期望收益为ps［p1(Rg2－Cr2+a1Tc+a2Tc)+(1－p1)(Rg2－Cr2)］+(1－ps)Rg2，即Rg2+ps(p1Tc(a1+a2)－Cr2)。显然，当ps(p1Tc(a1+a2)－Cr2)＞0，即期望罚款收益大于监管成本时，地方政府才会进行监管，此时的纳什均衡为(监管，不串谋)。若ps(p1Tc(a1+a2)－Cr2)＜0时，地方政府的最佳策略选择为不监管，供应网点的策略转向串谋，此时的纳什均衡为(不监管，串谋)。

(3)博弈Ⅲ:代储企业和供应网点间的博弈

突发事件发生后，在成品粮的配送与供应过程中，若一方努力，而一方投机，努力方发现投机方的行为必定向地方政府举报，政府将对投机方进行处罚，但对举报方却无奖励。

当代储企业不串谋时，不管供应网点采取何种策略，其收益均为R1i+L1i－C1i。若二者串谋，则代储企业的收益为R1i+L1i－C1i+∂Tc或R1i+L1i－a1Tc。若供应网点不与代储企业串谋，且发现了代储企业的投机行为，则代储企业的收益为R1i+L1i－C1i－a1Tc;若供应网点并没有发现代储企业投机行为，假设此时代储企业的收益也为 R1i+L1i－C1i+∂Tc。

供应网点不串谋时的收益为 R2j+S2j－C2j，串谋收益为 R2j+S2j－C2j+(1－∂)Tc或 R2j+S2j－C2j－a2Tc。若代储企业不与之串谋，并举报了其投机行为，则其收益为R2j+S2j－C2j－a2Tc;若代储企业没有发现供应网点的投机行为，此时其收益仍为R2j+S2j－C2j+(1－∂)Tc。则代储企业与供应网点之间的收益矩阵如表3所示。

表3 成品粮应急代储系统博弈Ⅲ的收益矩阵

由此可知，代储企业和供应网点的期望收益分别为p1［ps(R1i+L1i－C1i－a1Tc)+(1－ps)(R1i+L1i－C1i+∂Tc)］+(1 －p1)(R1i+L1i－C1i)和 p1［ps(R2j+S2j－C2j－a2Tc)+(1 －ps)(R2j+S2j－C2j+(1 －∂)Tc］+(1－p1)(R2j+S2j－C2j)，即(R1i+L1i－C1i)+((1－ps)∂－a1p)p1Tc和 R2j+S2j－C2j+((1－ps)(1－∂)－a2ps)p1Tc。

当((1－ps)∂－a1ps)p1Tc＞0，且((1－ps)(1－∂)－a2ps)p1Tc＞0时，即代储企业和供应网点的串谋期望收益大于地方政府的罚款时，(串谋，串谋)是博弈Ⅲ的纳什均衡，此时，即使地方政府进行监管，二者仍会串谋。当((1－ps)∂－a1ps)p1Tc＜0，且((1－ps)(1－∂)－a2ps)p1Tc＜0时，即地方政府的罚款大于二者的串谋期望收益时，若地方政府进行监管，则代储企业与供应网点的最优策略为不串谋，此时地方政府的最优策略转变为不监管;地方政府一旦不监管，则代储企业与供应网点就会进行串谋，地方政府则要进行监管。因此，博弈Ⅲ是混合策略博弈，不能自动形成一个稳定的均衡点，也不存在稳定的均衡解。

从博弈链的角度来看，各个博弈局势之间通过一定的作用机理产生影响。本文以代储企业和供应网点之间是否串谋为传递机制来研究三个博弈局势的均衡。如果博弈Ⅰ的均衡解为(监管，不串谋)，则博弈Ⅱ和博弈Ⅲ的均衡解分别为(监管，不串谋)和(不串谋，不串谋);如果博弈Ⅰ的均衡解为(不监管，串谋)，则博弈Ⅱ和博弈Ⅲ的均衡解分别为(不监管，串谋)和(串谋，串谋)。如果地方政府的罚款收益大于监管成本，其便会进行监管，则代储企业和供应网点的最佳策略均是努力，此时，整个博弈链的纳什均衡为(监管，不串谋，不串谋);如果地方政府的监管成本大于罚款收益，便不会进行监管，则代储企业和供应网点的最优策略就是串谋。反之，如果代储企业或供应网点一方的策略为串谋，则另一方的最佳策略亦为串谋，此时地方政府的最佳策略为监管;政府一旦监管，代储企业和供应网点的最佳策略转变为不串谋。

四、成品粮应急代储系统博弈链均衡分析

1.地方政府的最佳监管概率

基于成品粮应急代储系统博弈链模型的分析，地方政府在对代储企业和供应网点监管中的期望收益为

由(1)式可知，地方政府的期望收益是其监管概率的函数，对ps求导，得

由(2)式可知，代储企业与供应网点的最佳串谋概率与地方政府的监管成本成正比，与罚款收益成反比。即地方政府的监管成本越高，其监管的动力就越小，则代储企业和供应网点便有机可乘;地方政府的罚款力度越大，则代储企业和供应网点串谋的概率就越小。由此可知，可通过加大惩罚力度来降低代储企业和供应网点的串谋风险。

2.代储企业的最佳串谋概率

代储企业的最佳策略选择并非总是串谋，由博弈Ⅰ和博弈Ⅲ可知，代储企业的期望收益为:

从(3)式可见，代储企业的期望收益是其串谋概率的函数，对式中的p1求导得:

由(4)式可知，地方政府对代储企业的最佳监管概率与对其罚款力度和代储企业的串谋收益有关。若罚款力度大，就可以实行较低程度的监管;若代储企业的串谋收益大，政府的监管概率则要提高。

3.供应网点的最佳串谋概率

由博弈Ⅱ和博弈Ⅲ可知，供应网点的期望收益为:

供应网点的期望收益是其串谋概率的函数，对(5)式中的p1求导得出:

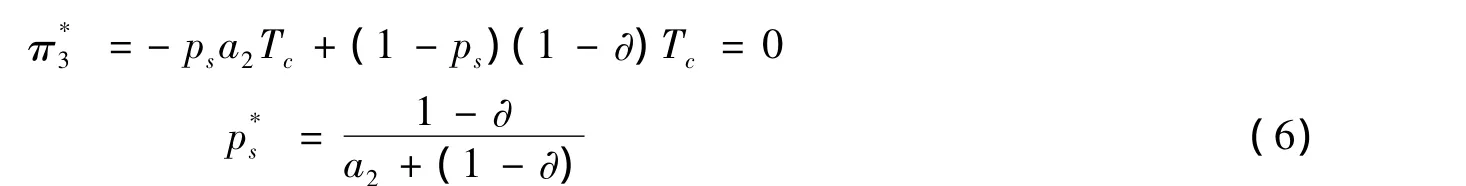
从式(6)可知，地方政府对供应网点的监管概率与供应网点受到的罚款系数和串谋收益系数有关。罚款系数越大，地方政府对供应网点的监管就可以适当降低;供应网点的串谋收益越大，则就越需要加强对供应网点的监管力度。

4.成品粮应急代储系统博弈链均衡解

通过对成品粮应急代储系统博弈链模型的分析可知，该博弈链的均衡解为:

地方政府可以通过调控政府监管成本，惩罚力度，以及代储企业和供应网点的串谋收益来实现对代储系统的良好控制，取得代储成本和应急效益的平衡。

五、对策建议

成品粮应急代储系统涉及利益相关者众多，其功能的有效发挥需要对不同利益主体进行协调，实现多部门、多主体的协同联动。由于主体间存在严重的信息不对称性，任何一个主体的策略变化都会影响整个系统的均衡状态。由影响成品粮应急代储系统均衡解的相关因素可知，地方政府在以后的工作中可从以下几个方面促进系统的协调发展。

1.建立科学的激励机制。成品粮储备是应急时的第一道生命保障线，其数量、质量和供应速度直接影响到受灾民众的生命安全。而目前地方政府对代储企业和供应网点除了一定的财政补贴外很少有其他的激励措施，形式单一，且不灵活。同时对企业的投机行为惩罚标准不明确、力度较小。因此，要从正、负两方面激励和督促代储企业和供应网点的行为，必须建立灵活多样的激励机制。

2.加强政府监管力度。地方粮食行政管理部门负责成品粮储备的日常管理和监管工作。由于代储企业和供应网点数量众多，而目前地方政府多采用人力督查的传统方式进行监管，效率低下的同时成本较高。从成品粮应急代储系统博弈链的均衡解中可以看出，地方政府必须在平衡监管成本和效益的基础上，利用计算机和信息技术，实现政府监管的实时性和连续性;引进现代化管理方式，创新管理理念，强化监管意识。

3.适时调整政府补贴标准。代储企业和供应网点的收益主要来自于政府补贴。随着经济的发展和物价水平的提高，代储企业和供应网点的运营成本逐年增加，但现行的储备粮补贴标准近二十年来未做调整，致使许多企业依靠多种经营辅业反哺粮油仓储主业，大大挫伤了企业的积极性。如北京市现行的储备粮补贴标准是1992年制定的，且当时的储粮对象仅是原粮，直至2010年才重新作了修订，还有许多省市至今未做调整。因此，地方政府要及时调整补贴标准，保证代储企业和供应网点的基本利益，以调动其合作的积极性。

4.创新成品粮轮换方法。轮换成本是代储企业运营成本的重要组成部分。相对于原粮，成品粮更强的腐败性决定了其具有更高的轮换频次，如小麦粉要求夏季(6、7、8月)每月轮换一次，其它季节45天轮换一次，并先进后出，且不能很好地利用市场规律，占用了企业大量资金。现在已有部分省市进行了轮换方法的创新，采取“动态均衡轮换制度”，按照储备粮实际库存的20%至30%分批轮换，保证轮换期间储备粮的实际库存量不得低于总规模的80%。另外，可引进市场机制，降低风险，提高轮换收益，激发企业的积极性。

5.完善粮食储备法律法规。目前，关于储备粮的国家级法规、规章、标准和技术规范尚不完善，地方标准也不统一。由于我国成品粮储备起步晚，关于成品粮储备几乎没有独立的法规、规章、标准和技术规范，大多是包含在储备粮相关政策法规里面。只有从法律法规的层面明确了政府、代储企业和供应网点各自的权益和义务，才能从根本上协调主体间的各种冲突，完善管理机制，促进代储系统健康快速地发展。

成品粮应急储备系统的完善和发展不仅要着眼于国内粮食市场，建立适合我国国情的粮食储备系统，更要与国际市场接轨，利用国际资源，构建稳定性更好的国际性粮食安全系统，积极实施大概念的“粮安工程”，进一步增强我国的粮食安全，提高我国政府的应急保障能力。

［1］Ben L，Andrew R.Grain Reserves and the Food Price Crisis:Selected Writings from 2008 – 2012［R］.Institute for Agriculture and Trade Policy，2012.

［2］侯光明等.组织系统科学概论［M］.北京:科学出版社，2006:157－164.

［3］Stolovitch，Harold D.Frame Games and Game Chains:A Technology for Interactive Teaching/Learning［J］.Viewpoints in Teaching and Learning，1982，58(3).

［4］胡明礼，刘思峰，方志耕，阮爱清.企业集群演进的进化博弈链模型研究［J］.科技进步与对策，2006，(11).

［5］钱春丽，侯光明，李存金.基于知识博弈链的军民两用高技术产业集 群协同创新机理研究［C］.香山科学会议第288次学术讨论会论文集，2008.

［6］陈洪转.基于链结构模型的区域产学研合作均衡研究［J］.软科学，2012，26(2).

［7］冯媛.基于博弈分析的设计链知识共享研究［J］.科技管理研究，2010，30(4).

［8］张昊宇，陈安.应急救灾三方博弈模型研究［J］.电子科技大学学报(社会科学版)，2011，13(3).

［9］黄婧，纪志耿.法律保护、合约选择及"三方"博弈行为分析［J］.经济与管理研究，2008，(4).

［10］陈福集，黄江玲.三方博弈视角下政府应对网络推手的对策研究［J］.中国行政管理，2013，(11).

［11］宋维佳.我国粮食储备体系重组的基本分析［J］.财经问题研究，2006，(3).

［12］Joachim V B，Maximo T.Implementing Physical and Virtual Food Reserves to Protect the Poor and Prevent Market Failure［J］.IFPRI Policy Brief，2009，(2).

责任编辑:蔡 强