地应力影响下隧洞边墙的爆破振动安全*
朱 俊,杨建华,卢文波,陈 明,严 鹏
(1.中国港湾工程有限责任公司,北京100027;2.武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉430072;3.武汉大学水利水电学院水工岩石力学教育部重点实验室,湖北 武汉430072;4.中交第四航务工程勘察设计院有限公司,广东 广州510230)
钻爆开挖是目前水电、交通、采矿和防护工程中边坡及地下洞室的主要开挖手段。爆破本身的瞬时性、复杂性以及爆破介质的多变性,使爆破开挖诱发的围岩损伤预测仍然存在较大的困难[1]。目前,在预测爆破振动损伤方面有了大量的工作。P.K.Singh[2]监测了印度某矿山露天爆破对地下洞室的影响,发现峰值质点振动速度(peak particle vibration velocity,PPV)达到113mm/s时,洞室有轻度损伤,并在洞顶部有小块体掉落,当PPV 达到181.9mm/s时,洞室损伤严重;M.Khandelwala等[3]采用神经网络方法预测爆破振动的PPV,判断爆破振动损伤,并将预测结果与实测数据多元回归所得的结果进行了对比。李新平等[4]结合溪洛渡水电站导流洞的开挖,采用FLAC-3D 软件模拟了爆破振动对相邻洞室的影响,并提出了基于拉应力准则的爆破振动安全判据;夏祥[5]分别运用LS-DYNA、FLAC、UDEC软件模拟了爆破中远区应力波和爆破振动的衰减,并在此基础上得到了爆破损伤范围,并提出相应的爆破振动安全判据;夏祥等[6]通过对红沿河核电站基岩爆破工程的实际检测,指出采用爆破临界峰值振动速度判定爆破损伤深度是合理的;J.H.Shin等[7]用数值模型计算了软岩条件下爆破对已有相邻洞室的影响。
目前,爆破振动对地下隧洞围岩的损伤与安全判据的研究中,对于地应力的影响较少考虑。对于浅埋隧洞,地应力影响可以忽略,但是对于处于中高地应力条件下的隧洞,地应力影响不可忽略。本文中,在已有研究的基础上,结合溪洛渡右岸5号导流洞的爆破开挖,考虑地应力,研究深孔梯段爆破激发的围岩振动对大跨度洞室本身安全的影响。
1 工程背景
溪洛渡水电站施工期右岸布置3条导流洞,洞身断面为城门洞型,断面宽为18 m、高为20 m。围岩主要为致密状玄武岩、斑状玄武岩及角砾熔岩,岩性坚硬,单轴抗压强度超过100 MPa。由于断面尺寸大,导流洞分3层爆破开挖。中层开挖高度11.0m,采取先预裂后梯段爆破的施工方法。主炮孔钻孔深度11.0m、孔距3.0m、排距2.5m、超深0.5m、孔径90mm,采用直径70mm 药卷连续装药,最大单响药量控制在60kg,爆破设计如图1所示。测点沿洞室轴线布置,间距10~20m,如图2所示。
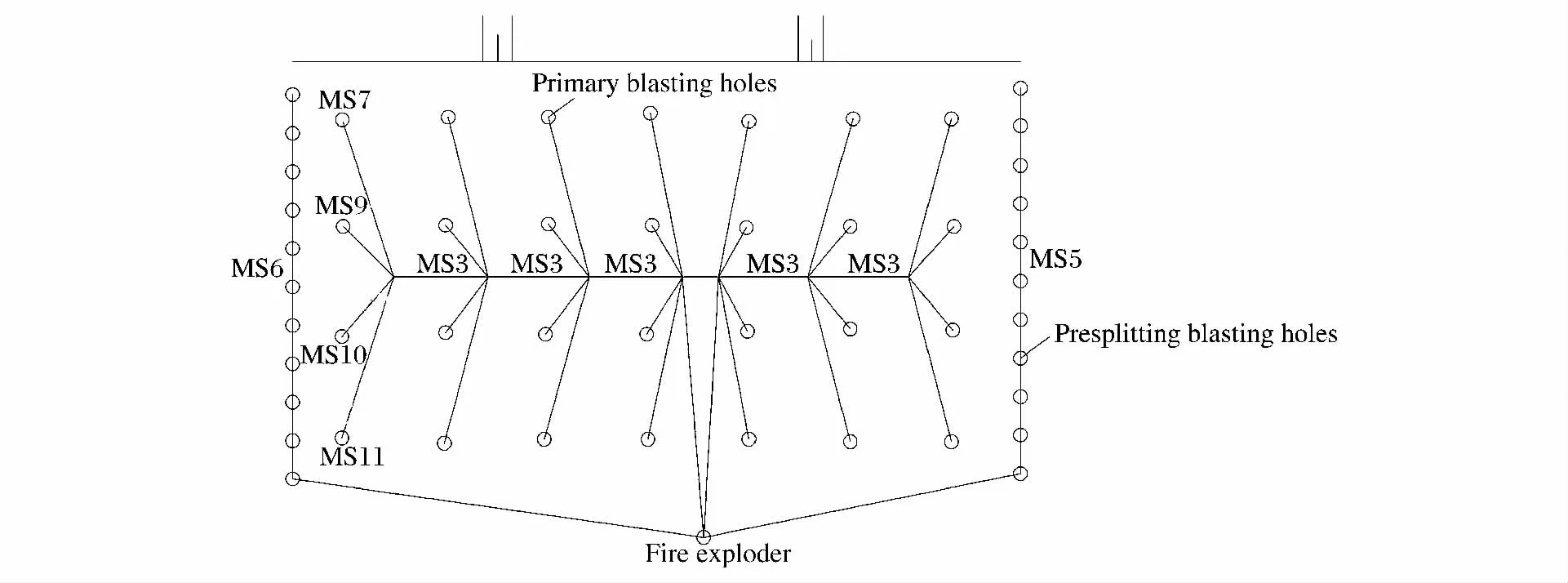
图1 中层开挖钻爆设计图Fig.1 Blast design of the second layer
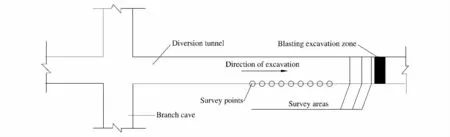
图2 爆破振动测点布置Fig.2 Layout of monitoring points on site
实测的峰值质点振动速度衰减规律为[8]:
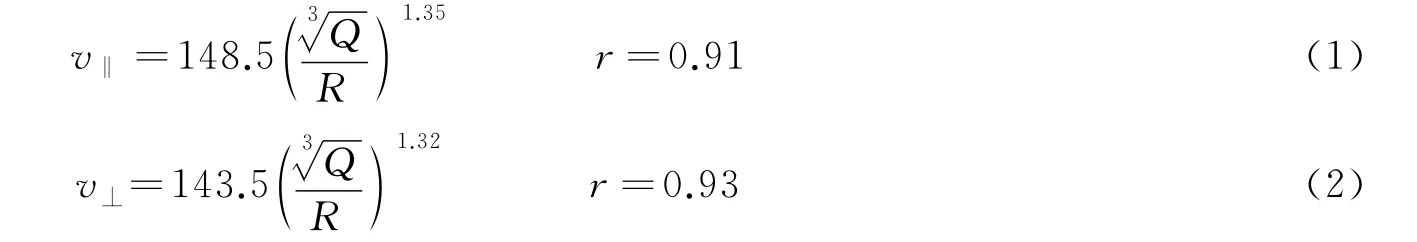
式中:v‖和v⊥分别为轴向和竖直向峰值质点振动速度,Q 为单响药量,R 为爆心距,r 为相关系数。
2 围岩爆破振动的数值模拟
对于微差爆破,选取最大段单响药量计算爆破振动的影响。考虑现场爆破多采用2孔1段起爆方式,本文中模拟2个垂直炮孔同时起爆。
2.1 计算模型
有限元计算模型如图3所示,计算区域长为100m、宽为90m、高为90m。为了消除人为边界处的反射波对动力响应的影响,设模型边界为无反射边界。采用塑性随动模型模拟岩体材料,弹性模量E=45GPa,切线模量ET=4.5GPa,屈服应力σy=60MPa,岩体密度ρ=2 700kg/m3,泊松比μ=0.23。溪洛渡工程区域为中等应力场区,应力场相对稳定。为简化计算,远场地应力采用均匀分布的面荷载。竖直向(y 向)地应力为6 MPa,水平向(x 向和z 向)地应力均为10 MPa[9]。对于洞室顶拱层部位,中层开挖时顶部已经完成了支护,因此对顶部的材料进行相应的强化处理。

图3 模型数值计算网格Fig.3 Mesh of numerical model
2.2 荷载与边界条件
炸药的爆轰过程复杂,而本文中主要研究爆破远区的振动与应力关系,根据圣维南原理,动力计算中,将爆破荷载加在炮孔周围粉碎区边缘。在CJ爆轰条件下,炸药的平均爆轰压力为[10]:

式中:pd为炸药爆轰平均初始压力;ρe 为炸药密度;D 为炸药爆轰速度;γ 为等熵指数;dc、db分别为装药直径和炮孔直径;le、lb分别为装药和炮孔的长度;n 为增大因数,n=8~11。
炮孔粉碎区边缘的峰值压力pm为[10]:
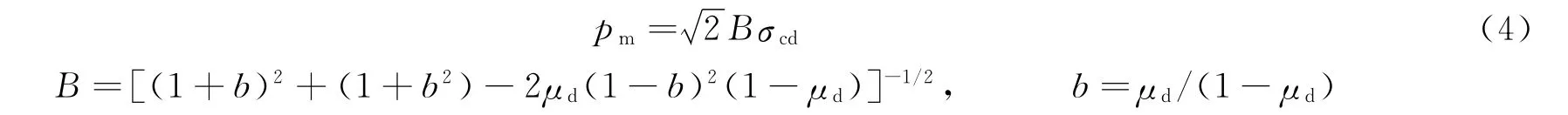
式中:σcd为岩体动抗压强度;μd 为岩体动泊松比。
粉碎区半径为[10]:

式中:rc、rb分别为粉碎区半径和炮孔半径;α 为冲击波衰减因数,一般取3。
根据式(3)~(5)可得,粉碎区边缘的峰值压力pm=136 MPa,粉碎区半径rc=172.8mm。采用三角形荷载曲线[11],取荷载上升时间tr=3ms、正压作用时间td=7ms。
2.3 数值模拟合理性评估
对实测数据点的峰值质点振动速度,采用萨道夫斯基公式回归分析,径线方向、垂直方向和轴线方向的振动速度的传播衰减规律为:
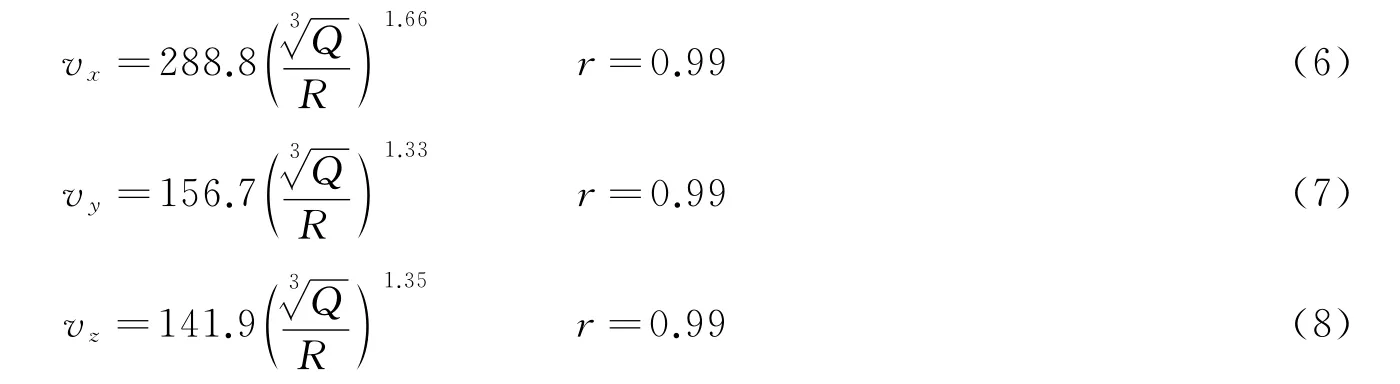
根据式(2)和(7),对比垂直方向现场实测数据和数值模拟分别回归分析得到的爆破振动变化规律,可以看到,实测数据与数值模拟结果较好吻合,这表明数值模拟的结果是可靠的。
2.4 洞室围岩轮廓面振速分布
在爆破开挖面后方(如图2所示),取离爆心距离分别为0.5、5.0和10.0m 的3个断面,洞室周边的峰值振动速度分布规律如图4所示。
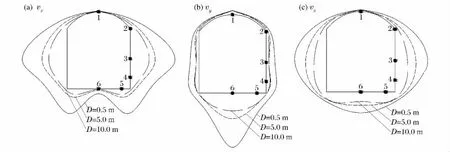
图4 洞室周边的峰值振动速度分布Fig.4 Distribution of peak vibration velocity
从图4可以看出:在水平方向(x 方向),质点峰值振动速度呈轴对称分布,在拱顶处与底面中心振动速度为约零,最大峰值质点振动速度出现在洞室断面直立墙中部,且在边墙部位振动速度较大;在竖直方向(y 方向),峰值质点振动速度呈轴对称分布,最大峰值质点振动速度出现在洞室断面底面中部,且在底面的峰值振动速度较大,在拱顶处分布较均匀;在边墙与下层台阶交界处,水平向与垂直向峰值振动速度都较大;在平行于洞室轴线方向(z 方向),质点峰值振动速度呈轴对称分布,最大峰值质点振动速度出现在洞室断面直立墙中部,且在边墙部位振动速度较大,在底部分部均匀,变化较小。
3 基于最大拉应力的爆破损伤判据
由于导流洞埋深较大,处于中等地应力水平,损伤不仅与爆破峰值质点振动速度有关,还与地应力重分布有关。溪洛渡工程地下洞室岩体的抗剪强度可达20 MPa[12],而岩石的抗拉强度较小,约4 MPa。以最大拉应力作为损伤判据,从动载单独作用(只考虑爆破产生的冲击荷载、不考虑地应力)和动静载共同作用(既考虑爆破冲击荷载、也考虑地应力)两方面,对比分析洞室围岩的损伤分布,提出考虑地应力影响的隧洞围岩爆破振动安全判据。假定拉应力为正值,压应力为负值,且σ1≥σ2≥σ3,σ1为最大主应力,σ2为中间主应力,σ3为最小主应力。
3.1 洞室围岩轮廓面应力分布
从振速分布(见图4),边墙与下层台阶交接处、拱座处、边墙中部及底板中部都是洞室容易发生破坏的危险区域。在爆破开挖面后方,取断面D=0.5m,动载单独作用时和动静载共同作用时的应力计算结果见表1。
由表1可以看出,动载单独作用下,洞室全断面均出现了不同程度的拉应力,最大拉应力与最大剪应力均出现在底板中部,并且在边墙中部拉应力和剪应力也较大,因此在边墙中部和地板中部在动载单独作用时容易出现拉剪破坏。
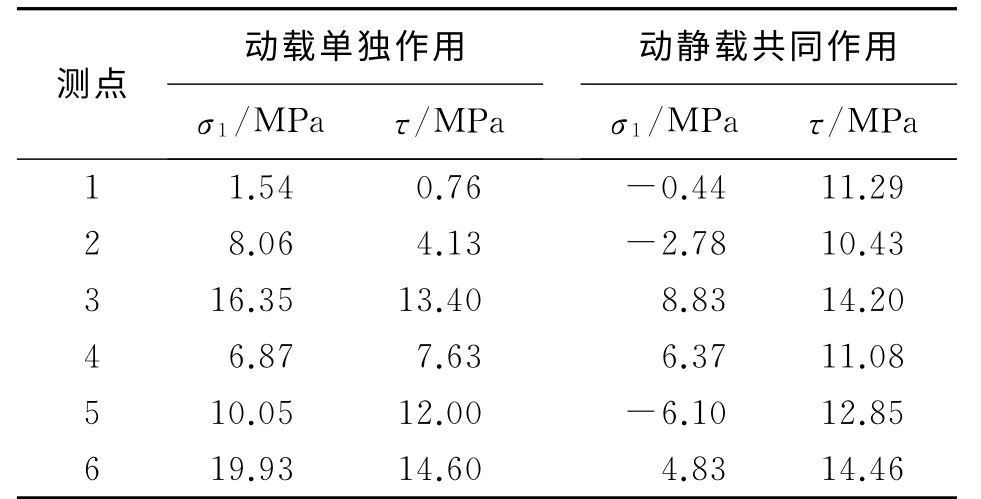
表1 洞室轮廓危险部位最大应力Table 1 Maximum stresses in dangerous area of underground diversion tunnel
动静荷载共同作用时,在边墙中部、边墙底部和底板中心出现拉应力,拉应力最大出现在边墙中部,同时边墙中部的剪应力也较大,因此在边墙中部容易出现拉、剪破坏。在墙角和拱座处出现压应力、剪应力集中,因此在动静载共同作用下,墙角和拱座最容易出现压剪破坏。
在计算中,模拟的是洞室分层开挖的中层开挖。而中层开挖时顶层的开挖以及支护已经完成,因此,拉应力不再是顶层爆破危害控制的主要因素,所以所测得的顶层拉应力较小。
动静载共同作用与动载单独作用相比,动静载共同作用时大部分测点最大剪应力均较大程度地增加,顶拱和拱座处以及底板边缘靠近边墙处的应力由拉应力变为压应力,断面最大拉应力由地板中部转移到边墙中部。因此,动静载共同作用时,容易在边墙和底板处产生拉、剪破坏。综合说来,动静载共同作用时,隧洞最容易出现破坏的部位是边墙中部,动载单独作用时,隧洞最容易出现破坏的部位是地板中部。因此,考虑地应力时,洞室的损伤判定与不考虑地应力时的损伤判定不同。
3.2 洞室围岩损伤范围
根据上述分析,在爆破开挖面后方,取边墙中部和底板中部的相应位置测点,其最大拉应力沿洞室轴向距离的衰减规律如图5所示。按照最大拉应力的损伤判别准则,动载单独作用时,中层梯段爆破开挖,在边墙中部的位置沿洞室轴向的损伤距离为14.33m,在底板中部的位置沿洞室轴向的损伤距离为约7.61 m;动静载共同作用时,中层梯段爆破开挖,在边墙中部的位置沿洞室轴向的损伤距离为2.36m,在底板中部的位置沿洞室轴向的损伤距离为约2.28m。计算结果表明,沿洞室轴向,爆破振动产生的损伤在边墙中部最严重,并且考虑地应力时爆破损伤范围与不考虑地应力时差别较大。
在爆破开挖面后方,取距爆心最近轮廓面边墙中部和底板中部的相应位置测点,其最大拉应力沿洞室径向距离的衰减规律如图6所示。动载单独作用时,中层梯段爆破开挖,在边墙中部的位置沿洞室径向的损伤距离为8.65m,在底板中部的位置沿洞室径向的损伤距离为约10.37m;动静载共同作用时,在边墙中部的位置沿洞室径向的损伤距离为约4.15m,在底板中部的位置沿洞室径向的损伤距离为约3.52m。在爆心平面所在的轮廓面,爆破振动产生的损伤在边墙中部最严重,并且考虑地应力时,爆破损伤范围与不考虑地应力时差别较大。
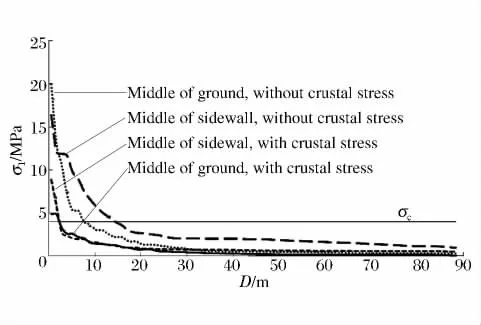
图5 最大拉应力沿洞室轴向衰减规律Fig.5 Attenuation law of maximum tensile stress in axial
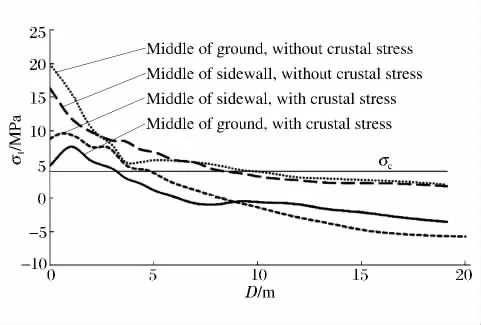
图6 最大拉应力沿洞室径向衰减规律Fig.6 Attenuation law of maximum tensile stress in radial
3.3 考虑地应力的爆破振动安全判据
采用峰值质点振动速度判据和最大拉应力准则所得的洞室损伤范围相近,因此可以认为峰值质点振速和最大拉应力具有一定的相关性,因此,可采用爆破振动峰值质点振速判定围岩的损伤。
在爆破开挖过程中,洞室轮廓面最大拉应力、最大振速出现在同一部位,即洞室的边墙中部,且最大主应力方向几乎与x 轴平行。因此,可以通过拟合x 向峰值质点振速与最大拉应力的关系,得到一定拉应力条件下的峰值质点振速的临界值。
对动载单独作用下的最大拉应力σth与动静载共同作用时的最大拉应力σtd进行线性拟合,拟合的线性关系较好,如图7所示。从图中可以看出,两个主应力相关性明显(相关系数r=0.997),呈现良好的线性关系,关系式为:

式中:σth为动载作用产生的最大拉应力,MPa;σtd为动静载共同作用时的最大拉应力,MPa。
根据杨建华等[11]的研究,爆破开挖所产生的振动仅由动载产生。因此,考虑振速和最大主应力的关系时,所采用的是主应力为动载所产生的主应力。
对动载作用产生的主应力与x 向振速进行数值拟合,如图8所示。
由图8可见,拟合的线性关系较好,相关性明显(相关系数r=0.982),呈良好的线性关系,关系式为:

变形可得:

式中:v 为振速,cm/s。
将式(9)、(11)联立,列可得动静载共同作用下的最大拉应力与振速的关系式:

对式(12)中的v、σtd进行相关性检验,可知两变量的相关系数为0.973,相关性较好。因此,可以根据式(12)估算有地应力情况下的临界振速。
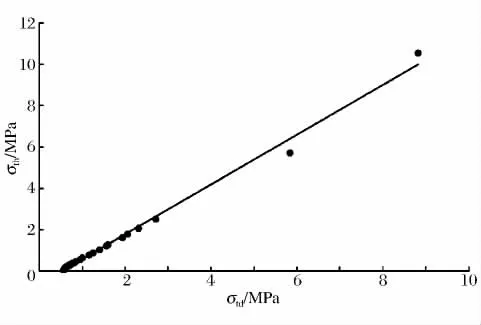
图7 动应力与耦合应力的数值拟合关系Fig.7Statistical relationship between dynamic stress and coupling stress
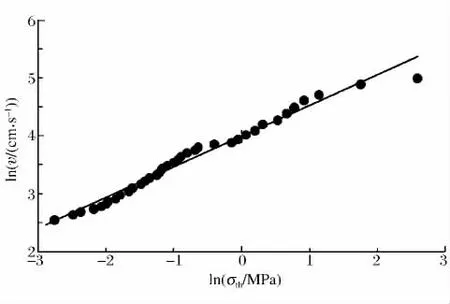
图8 动应力与x 向振速的数值拟合关系Fig.8Statistical relationship between dynamic stress and peak particle vibration velocity in xdirection
实际工程中,对于完整的地下洞室岩石,抗拉强度可取为3~4 MPa。此时,根据式(12)可得:v=97.55~116.77cm/s,即通过峰值质点振动速度判定围岩安全时,较完整的围岩洞室的临界峰值质点振动速度为97.55~116.77cm/s。对岩性较差的岩体,可取抗拉强度为1~2 MPa,此时,根据式(12)可得:v=40.68~74.15cm/s,即通过峰值质点振动速度判定围岩安全时,岩性较差的围岩洞室的临界峰值质点振动速度为40.68~74.15cm/s。
3.4 不同初始地应力条件下的围岩损伤临界振速
采用上述方法,可以得到不同初始地应力条件下的临界峰值质点振动速度,见表2。表中,σcru为初始水平地应力,侧压力因数β 为初始水平向地应力与垂直地应力的比,vc,p、vc,h分别为较差围岩临界振速、较好围岩临界振速。
从表2可以看出,无初始地应力时,洞室的临界振速小于有地应力的,这是因为有地应力时比无地应力时洞室不容易出现拉伸破坏。因此,根据拉应力所得的临界振速小于有地应力时的振速。

表2 不同初始地应力条件下的围岩损伤临界振速Table 2 The critical value of peak particle vibration velocity for damage under different geostresses
洞室围岩的损伤临界振速在侧压力因数较大时大于侧压力因数较小时的,且随着初始地应力的增大,洞室围岩的损伤临界振速逐渐降低。这是因为,在有初始地应力的情况下,围岩在爆破作用前洞室开挖后,地应力发生重分布,在洞室的轮廓面上有初始应力。爆破开挖后,洞室轮廓面上的应力为爆破荷载和地应力共同作用的结果。当洞室围岩应力达到损伤值时,初始地应力越大,侧压力因数越小,则爆破荷载引起的应力就越小。而对于围岩的振动,则主要由爆破产生的应力引起,爆破产生的应力越小,振动则越小。因此,根据振速应力关系所得到的围岩损伤峰值质点振速就越小。即当围岩的某点应力σt,max≥[σt]时,围岩被拉坏,而动载作用下某点应力σt=σtj+σtd,如果该点静应力σtj越小,则动应力σtd越大,即在允许抗拉强度相同的条件下该点能承受更大的动拉应力,也可承受较大的振动。
4 结 论
通过研究爆破振动对大断面洞室的影响,可得到如下结论:
(1)水平向振动对直墙影响较大,垂直向振动对洞室底面影响较大。爆破开挖过程中,洞室轮廓断面的最大振速和最大拉应力均出现在边墙中部,为水平径向振动速度。因此,边墙中部部位最容易产生拉伸破坏。
(2)损伤范围在地应力水平较大时小于不考虑地应力时的,因此,中高地应力水平情况下,地应力对爆破损伤的影响不能忽略。
通过研究地应力对地下隧洞边墙爆破振动安全阈值的影响,加深了对深部岩体爆破开挖损伤特性的认识,对研究深部岩体爆破振动损伤判据具有参考价值。
[1] 钱七虎.岩石爆炸动力学的若干进展[J].岩石力学与工程学报,2009,28(10):1945-1968.Qian Qi-hu.Some advances in rock blasting dynamics[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(10):1945-1968.
[2] Singh P K.Blast vibration damage to underground coal mines from adjacent open-pit blasting[J].International Journal of Rock Mechanics and Mining Sciences,2002,39(8):959-973.
[3] Khandelwala M,Singhb T N.Prediction of blast-induced ground vibration using artificial neural network[J].International Journal of Rock Mechanics and Mining Sciences,2009,46(7):1214-1222.
[4] 李新平,陈俊桦,李友华,等.溪洛渡电站地下洞室群爆破地震效应研究[J].岩石力学与工程学报,2010,29(3):494-500.Li Xin-ping,Chen Jun-hua,Li You-hua,et al.Study of blasting seismic effects of underground chamber group in Xiluodu Hydropower Station[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(3):494-500.
[5] 夏祥.爆炸荷载作用下岩体损伤特征及安全阈值研究[D].武汉:中国科学院武汉岩土力学研究所,2006.
[6] 夏祥,李海波,张大岩,等.红沿河核电站基岩爆破的控制标准[J].爆炸与冲击,2010,30(1):27-32.Xia Xiang,Li Hai-bo,Zhang Da-yan,et al.Safety threshold of blasting induced rock vibration for Hongyanhe Nuclear Power Plant[J].Explosion and Shock Waves,2010,30(1):27-32.
[7] Shin J H,Moon H G,Chae S E.Effect of blast-induced vibration on existing tunnels in soft rocks[J].Tunneling and Underground Space Technology,2011,26(1):51-61.
[8] 谭华,师锋民.溪洛渡水电站右岸导流洞洞室群开挖爆破试验[C]∥全国高拱坝及大型地下工程施工技术与装备经验交流会.2007:594-601.
[9] 李攀峰.金沙江溪洛渡水电站坝区地应力场及地下洞室群围岩稳定性数值模拟[M].成都:成都理工大学,2001.
[10] 戴俊.岩石动力学特性与爆破理论[M].北京:冶金工业出版社,2002.
[11] 杨建华,卢文波,陈明,等.岩石爆破开挖诱发振动的等效模拟方法[J].爆炸与冲击,2012,32(2):157-163.Yang Jian-hua,Lu Wen-bo,Chen Ming,et al.An equivalent simulation method for blasting vibration of surrounding rock[J].Explosion and Shock Waves,2012,32(2):157-163.
[12] 刘汉东,姜彤,黄志全,等.岩体力学参数优选理论及应用[M].郑州:黄河水利出版社,2006.

