多组分PBX炸药细观结构冲击点火数值模拟*
王 晨,陈 朗,刘 群,皮铮迪,胡晓棉
(1.北京理工大学爆炸科学与技术国家重点实验室,北京100081;2.北京应用物理与计算数学研究所,北京100094)
冲击起爆过程中,炸药首先受到冲击形成热点使炸药点火,然后反应进一步扩张,逐渐成长为爆轰。热点形成和点火过程与炸药细观结构有直接关系,研究炸药细观结构对冲击点火的影响是深入认识炸药冲击起爆机制的前提。由于技术的限制,从实验上还不能直接观测到冲击作用下炸药点火的过程。采用数学解析方法,又难以考虑非均质炸药复杂结构对冲击点火的影响。采用数值模拟方法可以描述炸药复杂细观结构,计算炸药内部不同组分界面的相互作用,为分析炸药冲击点火过程提供有效手段。
20世纪90年代起,人们开始开展炸药细观结构冲击点火的数值模拟。C.L.Mader等[1]以规则排布的空心圆球描述非均质炸药细观结构,对冲击作用下炸药响应过程进行了三维数值模拟,主要分析孔隙塌陷对热点形成的影响。P.A.Conley等[2]利用图像处理技术,将炸药细观结构扫描电镜照片转换成炸药细观结构计算模型,采用二维欧拉程序计算了冲击作用下PBX 炸药内部的温度分布,模型反映了炸药颗粒和粘结剂的不规则形状和分布。M.R.Baer[3]采用分子动力学的建模方法,建立了炸药颗粒尺寸和位置随机分布的三维炸药细观结构模型,分析了颗粒形状对炸药内部热点形成的影响。尚海林等[4]采用拼图方法构造三维炸药细观结构模型,采用离散元计算方法对PBX 炸药的冲击响应过程进行了研究,分析了炸药内部孔洞尺寸和形状对冲击响应的影响。A.Barua等[5]建立了细观条件下炸药颗粒随机分布的计算模型,分析了细观条件下炸药的响应过程。从现有研究情况看,人们在寻求不同的建模方法来构建炸药细观结构模型;数值模拟过程中只是对冲击作用下炸药颗粒间力学变形引起的温度变化进行计算,没有考虑炸药自身的反应,另外,计算模型与实际炸药结构还存在较大差距。
本文中,建立炸药颗粒自由堆积三维计算模型,模型中考虑炸药颗粒尺寸和位置的随机分布、粘结剂对炸药颗粒的包覆;采用非线性有限元计算方法,对炸药颗粒由自由堆积到密实装药的压药过程进行计算,求解PBX 炸药的细观结构模型;对多元PBX 炸药细观结构的冲击点火过程进行计算,考虑冲击作用下炸药内部热力的耦合作用和自热反应,分析炸药组分对冲击点火的影响。
1 PBX炸药细观结构
1.1 设计原理
PBX 炸药(plastic binder explosives)是一种塑料粘结炸药,由炸药颗粒、粘结剂等组成。炸药感度与炸药组分、颗粒度等细观结构相关。采用数值方法研究炸药的细观起爆机制,关键是获得炸药的细观结构。图1给出了一种PBX 炸药细观结构显微照片,可以看出,炸药颗粒呈不规则排列,形状、大小各异,粘结剂分布于炸药颗粒之间。
为获得炸药的细观结构,将炸药的压制过程考虑到细观结构模型构造中:先在一定尺度范围内构造炸药颗粒,将炸药颗粒装填在模具中,然后使用冲头冲压炸药颗粒,制得一定密度的装药。炸药压制过程中会出现颗粒变形、破碎和粘结剂重分布等现象,形成最终的炸药颗粒尺寸、分布以及粘结剂分布不规则的复杂炸药细观结构。
1.2 计算模型及参数
根据炸药压制原理,构建合理的炸药细观结构模型。根据图1所示PBX 炸药细观结构尺寸,构建一定数量的炸药颗粒,设未压前的炸药颗粒为球体,球体直径为一定范围内符合正态分布的随机取值,球体在一定空间内随机分布且相互没有重叠;每个球体外建立一定厚度的球壳作为粘结剂,粘结剂的厚度依据炸药和粘结剂的质量比确定,模型中炸药为HMX 和TATB,粘结剂为Estane;将这些球体装填在刚性模具中,构建成压药的原始模型,如图2所示。压药计算模型由冲头、刚性模具、炸药颗粒和粘结剂组成。把该模型导入有限元程序中,采用非线性有限元方法对压制过程进行计算[6]。计算中炸药上部为冲头加压面,其他3个方向为刚性壁面约束。冲头以一定速度向下移动,对炸药颗粒进行压制,外层包有粘结剂的炸药颗粒在冲头的作用下发生变形。根据不同的炸药密度,设定不同的冲头移动距离。通过控制压制后的炸药的最终体积,控制装药密度,获得PBX 炸药的细观结构模型。

图1 PBX 炸药细观结构显微照片Fig.1Image of the PBX microstructure
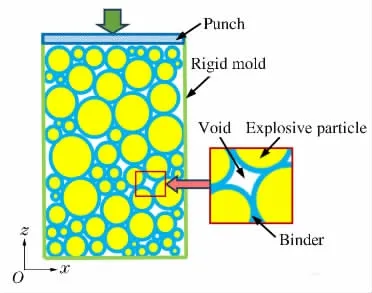
图2 炸药颗粒自由随机堆积示意图Fig.2 Pictorial of a packed ensemble of particles
模型中炸药颗粒和粘结剂Estane采用弹塑性流体力学材料模型和Grüneisen 状态方程描述。冲头和刚性模具材料为钢,不考虑其变形,采用刚体材料模型描述。表1 为材料参数[7],其中ρ 为材料密度,G 为剪切模量,σy为屈服应 力,c 为声速,s和γ0为Grüneisen状态方程参数。

表1 材料参数Table 1 Material parameters
1.3 计算结果
图3是HMX 炸药颗粒压制过程中不同时刻的变形图。冲头沿z 轴负方向移动,压制炸药。19μs时,冲头向下移动了很小的距离,大部分炸药颗粒基本没有变形,只是最上层的炸药颗粒在冲头作用下被冲压而变形;30μs时,上部的颗粒受到冲头作用影响,发生挤压变形和移动,使颗粒之间的孔隙减小,上部的炸药比下部更密实;55μs时,整个空间内的炸药颗粒已经发生很大变形,颗粒之间的孔隙已经很少;80μs时,冲头停止运动,炸药压制成型,整个炸药呈密实状态,密度为1.90g/cm3。
图4是计算得到的压制成型后的炸药细观结构截面图。从图4可以看出,整个炸药呈密实状态,炸药颗粒和粘结剂紧密接触,炸药内部基本没有孔隙。在冲头的作用下,初始状态为球体的炸药颗粒发生很大变形,炸药颗粒相互挤压变形并发生位移,粘结剂填充在炸药颗粒之间,使颗粒和粘结剂分布呈现不规则性。对比图1和图4可以看出,在炸药颗粒的大小、形状以及粘结剂的分布特征等方面,计算得到的炸药细观结构与实际炸药细观结构很接近,这表明采用该方法得到的炸药细观结构模型与真实的PBX 炸药细观结构相似,此模型可以有效描述PBX 炸药细观结构特征,即根据炸药压制原理获得的压药计算方法可以获得PBX 炸药的细观结构。

图3 压制过程炸药在不同时刻的变形Fig.3 Deformation of explosive particles at different times during compression

图4 计算得到压制成型后PBX 炸药细观结构截面图Fig.4 Calculated meso-structure of pressed PBXs
1.4 多元PBX炸药细观结构
PBXC10 炸药是一种由HMX 和TATB两种组分组成的混合炸药。根据PBXC10炸药中HMX 和TATB 的颗粒尺寸,建立不同HMX 和TATB比例的混合炸药自由堆积模型,模型中质量配比w1∶w2∶w3=88∶7∶5,76∶19∶5,67∶28∶5,57∶38∶5,38∶57∶5和29∶66∶5,其中w1、w2和w3分别为HMX、TATB 和Estane的质量分数。为了分析配方组成变化对多组分混合炸药冲击感度的影响,对以上6种配比的混合炸药的压药过程进行模拟,将炸药压制成1.90g/cm3的密实装药。图5是w1∶w2∶w3=38∶57∶5的炸药颗粒自由堆积模型。模型中有HMX 颗粒18个,颗粒尺寸为0.02~0.03mm,TATB颗粒98个,颗粒尺寸为0.015mm,所有颗粒自由装填在直径为0.1 mm、高度为0.3 mm 的刚性模具中。图6 为w1∶w2∶w3=38∶57∶5炸药细观结构1/2模型网格图。从图6可以看出,HMX 炸药颗粒变形较小,与HMX 相接触的TATB炸药颗粒变形较大。这可能是由于TATB的屈服应力比HMX 低,在颗粒相互挤压过程中,与HMX 接触的TATB颗粒更容易发生变形,而HMX 变形较小。此外,在TATB颗粒密集区,TATB颗粒的屈服强度相同,颗粒相互挤压引起的变形也相对较小。图7是压制完成后,6种配比炸药的细观结构。从图7可以看出,混合炸药压制完成后,HMX 和TATB都发生很大变形,颗粒交错分布。

图5 炸药颗粒自由堆积模型Fig.5 Packed ensemble of particles

图6 炸药细观结构1/2模型网络图Fig.6 Mesh of the calculation model

图7 不同配比混合炸药细观结构模型Fig.7 Calculated meso-structure for varying compositions
2 炸药细观结构冲击点火计算
PBXC10炸药内各组分的比例、尺寸等将会影响炸药的细观结构,从而导致炸药冲击感度变化。目前混合炸药组成配方都是根据经验或实验来确定,缺乏定量的方法指导,采用炸药压制原理建立混合炸药细观结构模型,计算不同组分比例混合炸药的冲击点火性能,可以为炸药配方设计提供定量指导。本文中采用非线性有限元计算方法,对PBX 炸药细观结构冲击点火过程进行数值模拟,分析混合炸药组分对炸药冲击点火的影响。
2.1 计算模型及参数
设计飞片冲击加载PBX 炸药细观结构的物理模型,如图8所示。模型由飞片、隔板和被测炸药组成。计算中,飞片以一定速度撞击隔板,产生的冲击波经隔板衰减后作用于PBX 炸药。模型中PBX 炸药直径为0.08mm,高为0.095mm,飞片和隔板的直径均为0.08mm,厚度均为0.01mm。图9为建立的飞片冲击加载PBX 炸药计算模型网格图。模型中飞片和隔板网格尺寸均为0.004mm,炸药网格根据颗粒尺寸大小确定。

图8 飞片冲击加载PBX 炸药物理模型Fig.8 Calculation model of shock to ignition

图9 飞片冲击加载PBX 炸药计算模型网络图Fig.9 Mesh of the calculation model
模型中HMX 和Estane都采用弹塑性流体力学材料模型和Grüneisen状态方程描述。飞片和隔板材料为钢,采用塑性动力学材料模型描述。弹塑性动力学材料模型的应力表示为:

式中:σ 为应力,σ0为初始屈服应力是应变率,C 和P 是Cowper-Symond应变率参数,是有效塑性应变,Ep是塑性硬化模量,β 为硬化参数。Grüneisen方程为:
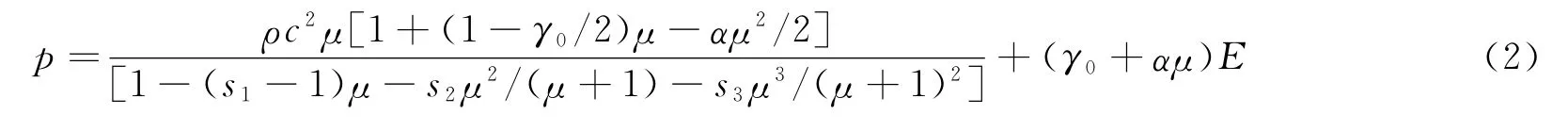
式中:p 为压力;μ=ρ/ρ0-1=1/vr-1,ρ0 为初始密度,vr为相对体积;E 为内能;s1、s2和s3为冲击波波速-波后粒子速度曲线的斜率系数;α 为一阶体积修正因数。
采用各向同性热材料模型来描述炸药和粘结剂的温度变化,实现热力耦合分析。根据能量守恒原理,热问题有限元方程可由热平衡方程推导求得[6]:

式中:C 为比热容矩阵,用于考虑系统内能的增加;KT为热传导矩阵,包括导热系数、对流系数以及辐射率和形状系数;T 为节点温度向量为温度对时间的导数;Q 为节点热流率向量。
热力耦合计算的基本方程为:

除了炸药受力发生变形引起温升外,炸药自热反应放出的热量也会引起温度的升高,两者共同作用最终引起炸药点火。采用Arrhenius方程描述炸药自热反应:

式中:S 为放热源项,Q 为反应热,Z 为指前因子,Ea为活化能,R 为普适气体常数,T 为温度。计算中,HMX 炸药的反应热为2 100J/g,指前因子为5×1019s-1,活化能为221 340J/mol;TATB炸药的反应热为2 520J/g,指前因子为3.18×1019s-1,活化能为251 600J/mol[8]。
2.2 计算结果分析

图10 温度分布图Fig.10 Distribution of temperature

图11 测点示意图Fig.11Schematic of gauging point

图12 炸药内部监测点温度时间变化曲线Fig.12 Calculated temperature-time curves of selected elements
HMX炸药具有较高的能量,同时较敏感,TATB炸药的能量较低,很钝感,因此为了达到炸药既钝感又高能的目标,现在炸药配方设计采用HMX和TATB混合的结构。混合炸药中各组分含量不同,导致炸药冲击感度有一定 差 别。对6 种HMX、TATB、Estane配比混合炸药的冲击点火过程进行计算,分析炸药组分对冲击点火的影响。图10 给出了在压力为5.3GPa的 冲 击 波 作 用 下,w1∶w2∶w3=38∶57∶5的混合炸药在0.01μs时的截面温度分布。从图10可以看出,0.01μs时,冲击波传播到炸药内部0.03mm 处,在冲击波经过的区域内,TATB 炸药颗粒的温度较高,而HMX 炸药颗粒的温度相对较低;局部高温区主要分布在与HMX 炸药颗粒相接触的TATB 上。这可能是由于与HMX 相接触的TATB 在压药过程中发生了较大变形,在冲击作用下更容易被压缩,温度升高较大。而HMX 颗粒在压药过程中变形相对较小,颗粒能够保持较好的完整性,在冲击波作用下温度升高较小。在距离炸药上表面0.025mm 处设置2个温度监测点,1号监测点位于TATB颗粒,2号监测点位于HMX 颗粒,如图11所示。图12是监测点处温度时间变化曲线。可以看出,1号监测点的最高温度达到453K,2号监测点的最高温度达到396K,表明TATB颗粒的温升比HMX 颗粒大。以上分析表明,炸药压药过程中变形较大的颗粒,在冲击作用下容易产生较大的温升。
采用不同速度的飞片撞击混合炸药,获取各种炸药发生点火的临界压力以及点火点位置。图13给出了临界点火压力加载下,不同配比炸药点火的细观结构、温度分布和点火位置。可以看出,尽管HMX 炸药的冲击感度较高,但各种配比炸药的点火点都出现在TATB 中,且都位于TATB 与HMX的界面上,这表明混合炸药冲击点火并不一定是由冲击感度较高的炸药组分引起,而是与炸药细观结构有很大关系,炸药压药过程中发生变形较大的炸药颗粒很可能首先点火。因此,在炸药配方设计中,应侧重于炸药各组分之间屈服强度的匹配以及压药工艺,尽量保证压制成密实状态的炸药颗粒的完整性,降低其冲击感度。
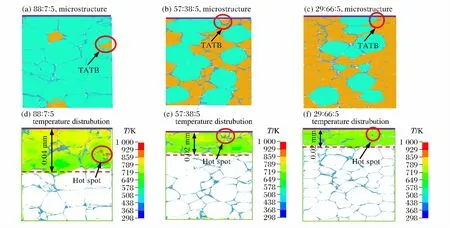
图13 不同配比炸药发生点火的位置Fig.13 Temperature contous of varying composite content

图14 临界点火压力随HMX 质量分数变化曲线Fig.14 Critical pressure of ignition varied with mass fraction of HMX
图14 为炸药的临界点火压力随HMX 含量变化曲线。从图14可看出,w1∶w2∶w3=29∶66∶5的炸药的临界点火压力为7.3GPa,w1∶w2∶w3=88∶7∶5的炸药的临界点火压力降低到4.6GPa。随着HMX 含量的增加,炸药发生点火的临界压力逐渐降低,炸药的冲击感度提高。这是由于HMX 含量增加后,混合炸药中TATB 颗粒与HMX 颗粒的接触界面增大,在炸药颗粒压制过程中发生大变形的TATB颗粒数量增加,使得混合炸药中潜在热点的数量增加,因此炸药更容易发生点火。
3 小 结
对多元PBX 炸药细观结构的冲击点火过程进行了数值模拟,采用炸药压制原理建立了混合炸药的细观结构模型,计算了不同组分质量分数的混合炸药的冲击点火性能。
(1)建立了炸药颗粒尺寸和位置随机分布三维自由堆积计算模型,通过对炸药颗粒由自由堆积到密实装药的压药过程的计算,获得了多组分混合炸药的细观结构模型。
(2)HMX 和TATB混合炸药压药过程中,与HMX 相接触的TATB变形较大,冲击作用下混合炸药点火点位于这些大变形的TATB内;混合炸药中TATB含量增加,炸药冲击感度降低。
[1] Mader C L,Kershner J D.The heterogeneous explosive reaction zone[C]∥Proceedings of 9th International Symposium on Detonation.Portland,Oregon,USA,1989.
[2] Conley P A,Benson D J.Microstructural effects in shock initiation[C]∥Proceedings of 11th International Symposium on Detonation.Snowmass,Colorado,1998:768-787.
[3] Baer M R.Modeling heterogeneous energetic materials at the mesoscale[J].Thermochimica Acta,2002,384:351-367.
[4] 尚海林,赵锋,王文强,等.冲击作用下炸药热点形成的3维离散元模拟[J].爆炸与冲击,2010,30(2):131-140.Shang Hai-lin,Zhao Feng,Wang Wen-qiang,et al.Three-dimensional discrete element simulation of hot spots in explosives under shock loading[J].Explosion and Shock Waves,2010,30(2):131-140.
[5] Barua A,Zhou M.A Lagrangian framework for analyzing microstructural level response of polymer-bonded explosives[J].Modelling and Simulation in Materials Science and Engineering,2011,19(5):1-24.
[6] Lawrence Livermore National Laboratory.LS-DYNA user’s manual[M].California:Lawrence Livermore National Laboratory,University of California,2001.
[7] 董海山,周芬芬.高能炸药及相关物性能[M].北京:科学出版社,1989:334-340.
[8] Gibbs T R,Popolato A.LASL explosive property data[M].California:University of California Press,1980:6-7,156-157.

