从范畴类型逻辑看蒙太格语法的被动转换规则
崔佳悦,邹崇理
(1.中国社会科学院研究生院,北京100732;2.中国社会科学院哲学研究所,北京100732)
从范畴类型逻辑看蒙太格语法的被动转换规则
崔佳悦1,邹崇理2
(1.中国社会科学院研究生院,北京100732;2.中国社会科学院哲学研究所,北京100732)
蒙太格语法是对范畴语法的继承,其句法规则采纳的是“毗连运算”这种遵循范畴语法函项应用原则的操作。但是在蒙太格语法中体现被动转换操作的扩展规则那里似乎看不到范畴语法的作用,被动转换规则是否遵循范畴语法的规律?以蒙太格语法对英语被动句——“结构被动句”的分析为例,从范畴语法的现代版本——范畴类型逻辑的视角来审视蒙太格语法的转换过程,获得的结论是:范畴类型逻辑提供的工具可以证明被动句转换的合理性,蒙太格语法扩展的被动转换规则同样遵循了范畴语法的规律。
蒙太格语法;转换规则;范畴语法;范畴类型逻辑;结构被动句
转换生成语法(Transformational Generative Grammar,简称TG)由美国著名语言学家乔姆斯基(N. Chomsky)在20世纪50年代创立。半个多世纪以来,TG成为国内外语言学领域中最有影响的语言学理论之一,TG的提出被誉为语言学界的“哥白尼似的革命”。TG的主要不足是缺乏关于自然语言语义的系统理论,而蒙太格语法(Montague Grammar,简称MG)为弥补这个缺欠,给自然语言的句法生成配置了语义的描写。MG句法规则的基本操作“毗连运算”来源于范畴语法(Categorical Grammar,简称CG)的函项应用原则,但MG对TG转换规则的描述似乎从中看不到CG的作用。因此MG是否完全遵循CG的规律是令人质疑的。本文针对这一问题,通过被动句转换的具体实例,用范畴类型逻辑(Categorical Type Logics,简称CTL)①范畴类型逻辑是范畴语法发展的最新阶段,扩大了范畴语法的表达力。所提供的工具证明:MG刻画被动转换的扩展规则同样遵循了CG的规律,而CG是适合于计算的语法理论。本文的工作是从计算机信息处理角度审视MG被动转换规则的研究结果。
一、相关背景
(一)蒙太格语法
蒙太格语法(MG)是美国逻辑学家理査德蒙太格(Richard Montague)用数理逻辑方法研究自然语言的形式语义学理论。MG的研究提供了将句法的生成与语义的组合相对应的模式,受到越来越多的语言学家和哲学家的关注,与MG及形式语义学相关的学术著作和学术论文不断出版和发表。托马森(Thomason)的“Formal Philosophy”(1974)和帕蒂(Partee)主编的“Montague grammar”(1976)等著述对蒙太格语法的早期推广起到了非常重要的作用。道蒂(Dowty)的“Word meaning and Montague grammar”(1979)及道蒂、华尔和皮特斯合著的“Introduction to Montague Semantics”(1981),以Gamut命名的荷兰学者合著的“Logic,Language,and Meaning”(1991),卡恩(Cann)的“Formal Semantics:An Introduction”(1993)等著述在学术界都负有盛名。近年在由荷兰著名学者范本瑟姆(Benthem)和美国学者穆伦(Meulen)主编的鸿篇巨制“Handbook of Logic and Language”(2011)中,MG作为首篇得到系统深入的阐释。
蒙太格语法来源于乔姆斯基的转换生成语法,基于转换生成语法确立了蒙太格语法的句法部分。在著名的PTQ英语部分语句系统中蒙太格共制定了17条句法规则S1-17,其中有基本规则(S1-S3),有函项应用规则(S4-S10),有合取与析取规则(S11-S13),有量化规则(S14-S16),最后一类是时态与记号规则(S17)[1]。
然而蒙太格语法句法规则中的句法操作却遵循了范畴语法的原则。我们以语句系统中第二类函项运用的规则S4和S5为例:
S4.若α∈PT且β∈PIV,则F4(α,β)∈Pt。而F4(α,β)=αβ′,并且β′是把β中的第一个动词置换成它的现在时第三人称单数而得到的结果。
S5.若α∈PTV且β∈PT,则F5(α,β)∈PIV。这里若β≠hen,F5(α,β)=αβ;若β=hen,F5(α,β)=α himn。
上述两条规则中的句法操作F4和F5体现了范畴语法的思想。这里句法操作的作用是把两个表达式毗连在一起,被毗连的两个表达式其中一个属于函子范畴,而另一个属于主目范畴。如“F4(α,β)=αβ′”中α可以是专名“John”,所属的函子范畴是S/(NPS),β可以是动词“walk”,所属的主目范畴是NPS,αβ′就是句子“John walks”,所属的结果范畴是S。S4告诉我们:由α和β进行毗连得αβ′,其背后隐藏着函子范畴S/(NPS)对主目范畴NPS向前运算得到结果范畴S的过程,这里的句法操作体现出范畴语法最基本的运算规律——函项应用原则。
蒙太格语法是转换生成语法的延续继承。针对PTQ系统的句法规则只能产生TG转换生成语法所谓的核心句(基本句式)这个局限,Partee等学者做了大量的、多方面的工作,扩展了MG的表达力,使MG能够进一步生成TG转换部分获得的非核心句(如被动句)。Partee对MG的修正有:将蒙太格句法规则使用的语符串(strings)表述方式改为加标括号(labeled bracket)式的表述;更重要的是创立了6条扩展规则来描述TG的转换内容,据此获得自然语言的被动、施事主语省略、宾语提升和主语提升等一系列转换句式[2]。而Partee的学生Bennett则充分拓宽了MG的句法规则,分为基本规则(3条)、函项应用规则(18条)、被动转换规则(6条)、合取析取规则(1条)、否定规则(4条)、量化规则(3条),共35条。其中的被动规则对被动句的主语施事和宾语受事的位置调换这一现象缺乏描述,整个转换过程的刻画不够完整。
蒙太格语法在自然语言的句法分析方面较之转换生成语法更严谨,逻辑性更强。乔姆斯基的转换生成语法是蒙太格语法的来源理论,后者胜过前者的原因除了有在句法基础上添加了语义描述外,还在于后者的句法分析建立在与自然语言信息处理密切相关的范畴语法基础上,其句法规则所体现的“毗连运算”操作是范畴语法的核心——函项应用原则。然而,MG描述转换思想的扩展规则跟范畴语法的关系尚不明朗,是否也是建立在范畴语法的基础上,或者说,转换规则刻画的过程是否同样遵循范畴语法的规律尚需论证。
(二)范畴语法和范畴类型逻辑
范畴语法是适合于计算的语法理论,其思想最初源于弗雷格(A.Frege)。其完整的表述归功于上世纪30年代的波兰逻辑学家列斯尼夫斯基(ksniewski)和爱裘凯维茨(Ajduciewcz)[3]。50年代初美国计算语言学家希勒尔(B.Hillel)出于机器翻译的需要发展了范畴语法。50年代末数学家兰贝克(J.Lambek)提出范畴语法的演算系统。
在范畴语法看来,自然语言分为两个基本范畴:名称范畴NP和句子范畴S,由这两个基本范畴派生出其他范畴;自然语言由小到大的生成可以通过其构成部分所属范畴的逐级运算来实现。范畴运算规则有:
(1)若α是属于范畴B/A的表达式并且β是属于范畴A的表达式,则αβ是属于范畴B的表达式。
(2)若α是属于范畴A的表达式并且β是属于范畴AB的表达式,则αβ是属于范畴B的表达式[4]。
比如说:表达式“love”属于范畴(NPS)/NP,表达式“Mary”属于范畴NP,两个表达式的毗连“love Mary”按照规则(1)就属于范畴NPS。表达式“John”属于范畴NP,它跟属于范畴NPS的表达式“Love Mary”毗连,按照规则(2)就获得属于范畴S的表达式“John loves Mary”。上述规则的运用由英语词条生成英语句,其“毗连运算”的操作体现出函项应用的原则,这也是蒙太格语法句法规则的基本思想。
上个世纪80年代中期到90年代末范畴语法逐渐走向繁荣。在这一时期,Steedman等人提出组合范畴语法CCG,Capenter等人发展了类型逻辑语义学。新世纪以来,Morrill和Moortgat的工作从范畴运算的算子和毗连的结构规则两方面丰富了Lambek演算,提出范畴语法的非连续系统和混合的多模态系统,这些是范畴语法的范畴类型逻辑发展方向[5]。
范畴类型逻辑CTL将语言学研究和数学逻辑运算更紧密地结合在一起,CTL的研究对自然语言的计算机分析显示出应用价值。CTL的基本原则是:语言认知就是数学计算,语法分析就是逻辑推演。CTL
不仅可以抽象地研究自然语言句法范畴的运行规律,还能够通过引入简单类型λ-演算的工具来展现句法和语义的接口(interface)[6]。
范畴类型逻辑在传统范畴语法描述“毗连运算”的函项原则基础上,增加了“交换”、“结合”、“添加”和“缩减”等一系列结构规则。CTL有Gentzen风格的矢列表述,用于讨论判定性问题;有树模式表述,用于直观展示句法生成和语义组合的并行推演;还有公理表述伴随可能世界的框架语义解释,据此讨论系统的可靠性和完全性。所有这些使得范畴类型逻辑作为研究自然语言的工具,其精准性远远强于传统意义上的范畴语法。因此,对自然语言的转换所涉及的“成分变动”和“成分增减”等现象都能给予充分解读。
为解答蒙太格语法中的转换规则是否具有范畴语法依据这样的问题,我们列出所需要的CTL的LP系统如下:
公理:(共三条)
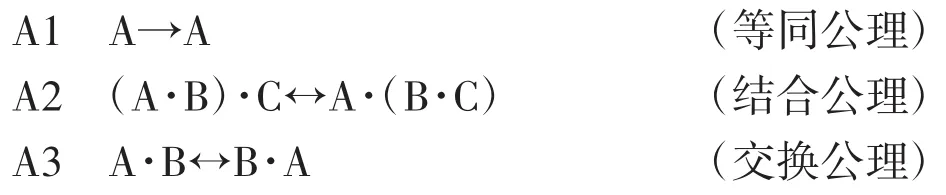
规则:(共五条)

本文第二部分针对英语被动句,采用蒙太格语法的转换规则推演出不同类型的被动句,通过范畴类型逻辑的LP系统所提供的工具,证明有关转换过程的合理性,从而论证MG的转换规则同样具有范畴语法的依据。
二、用CTL分析MG的被动转换规则
章振邦先生认为在语用学框架下划分被动结构的方式由“标记理论”支撑。这一理论认为,英语被动结构可以划分为“无标记结构”和“有标记结构”。“无标记结构”指的是“意义被动”,“有标记结构”称作“结构被动”[7]。如:
(1)The scientific equipment sells well.(这台科学仪器很畅销。)
(2)Friction can be reduced and the life of the machine prolonged by lubrication.(润滑能减少摩擦,延长机器寿命。)
以上(l)是“意义被动”,以主动语态表达被动含义,而(2)是典型的结构被动,因为它含有一种形态标记“be/get+过去分词”[8]。美国哥伦比亚大学语言学者肯尼斯认为:结构被动语态是一个有连接动词的语法标记(系动词),其后紧跟着动词的过去分词。下面我们讨论结构被动句法的情况,意义被动句的转换留待今后。
在本文第一部分我们看到,蒙太格语法的句法规则分为两大类:一类规则的任务是生成转换语法所谓的核心句。如S4:若δ∈PNP且ξ∈PVP,则F4(δ,ξ)=δ ξ′且F4(δ,ξ)∈PS。这类规则中的句法操作大都遵循范畴语法的函项运用原则,这些规则主要通过“毗连运算”进行操作,而“毗连运算”体现了范畴语法所谓由函子范畴对主目范畴进行计算的思想。如句法操作“F4(δ,ξ)=δ ξ′”表明由δ的范畴s/(s/np)对ξ的范畴s/np进行函项应用获得δ ξ′的范畴s。F4意味:输入的两个表达式的范畴之间进行一次运算得到其输出表达式的范畴,这就是F4体现的范畴语法原则,也是句法规则S4的范畴语法依据。
蒙太格语法另一类句法规则是扩展的转换规则,这类规则获得包括被动句在内转换结果。如Partee提出的结构被动句转换规则:
如果φ∈PS,且φ形如两种模式之一:
(a)严格模式:S[T[α]IV[TV[β]T[himi]]]
(b)非严格模式:S[T[α]IV[TV[β]T[δ]γ]]
则F101(φ)∈PS,其中F101(φ)为
例子:F101(Mary loves John)=John is loved by Mary。
就句法操作F101而言,输入的φ其范畴是S,输出的结果F101(φ)其范畴也是S,这个过程似乎没有显示范畴之间的运算。显然,转换规则中的句法操作F101不像前面生成核心句的句法规则中的F4那样,关注输入的两个表达式所属范畴之间的运算是否获得输出表达式所属的范畴。可见,考察MG的转换规则是否具有范畴语法的合理依据应该采取另外的视角。F101针对的是一个由几个表达式构成的主动句整体,经F101的运算使这个语句内部的成分发生一些变化:有些成分位置移动变换(主语名词和宾语名词),有些成分形态发生变化(动词),还增添了一些原来没有的新成分(或减少一些成分)。F101忽略了这些变化背后是否具有范畴语法的合理依据,是否隐藏着范畴类型逻辑潜在的运作机制,即并不关心形态改变后的动词其范畴跟动词原型的范畴是否相同,增添的成分指派什么样的范畴,F101强调的只是:输出的被动句其范畴也是S,但怎样得来并不在关注。
范畴语法却在意这些问题,范畴语法近20年发展迅猛的新分支——组合范畴语法CCG尝试解决MG转换规则带来的上述问题。CCG改变TG和MG把语言分为深层结构和表层结构的做法,认为自然语言是单层结构的,不需要由深层结构转换到表层结构。F101输入的主动句其内部成分被指派适当的范畴后,经过一次或多次运算获得范畴S。而F101输出的被动句其内部成分也需要指派合适的范畴(指派的范畴未必和主动句的相同),最终目的使得被动句内部成分的范畴运算也能得到S。依照CCG,主动句的范畴指派及其运算为:

被动句的范畴指派及其运算可能是①对于这里的被动句,考虑到系动词“is”和介词“by”在语义上是虚无所指的,故处理成恒等函项对应的范畴。当然CCG对被动句中成分范畴的指派还可能做另外的选择,如把“loved”的范畴同动词原型一样指派成“(np1s)/np2”,给系动词“is”指派的范畴做相应调整,最终结果要使被动句各成分的逐级运算也获得范畴S。另选什么方案并不影响我们要说明的观点:CCG并不关心主动句各成分的范畴指派与被动句各成分的范畴指派有什么关联。:

毋庸置疑的是,CCG是孤立看待主动句和被动句各自的范畴指派及其运算的。主动句是合语法的句子,给它的成分指派适当的范畴,经过逐级运算可得S。被动句也是合语法的句子,也能够运算得S。F101输入的主动句如何进行范畴运算得S跟F101输出的被动句怎样运算得S是没有关联的。换句话说,给φ内部各成分指派的范畴系列的毗连是否能够推出给F101(φ)内部各成分指派的范畴系列的毗连?如果能够推出,依据什么样的范畴类型逻辑工具?甚至给被动句中的动词变体指派的范畴为什么不同于给主动句中的动词原型指派的范畴?两者是否有关联?从逻辑的视角看,这些都是有意义的问题,是值得探究的工作。
通常认为,MG扩展的转换规则中的句法操作并不直接符合函项运用的范畴语法要求,这些规则中有添加的操作,添加系动词“be”和介词“by”;位置变动的操作,如施事名词和受事名词的位置变换;词条形态改变的操作,如动词原型在被动句中变成了动词的过去分词。我们的看法是:仅仅根据范畴语法最简单的函项运用原则,MG被动转换规则中句法操作的合理性得不到说明。但是依靠范畴语法最新版本——范畴类型逻辑所提供的工具,综合调动其中的结合、交换等结构规则和单调律等手段,可以在CCG
停顿的地方继续前进,从新的视角考察被动转换规则的句法操作的范畴语法合理性,即从给主动句各成分指派的范畴系列推出给被动句各成分指派的范畴系列,从而证明MG扩展的转换规则同样具有范畴语法的可计算依据。
Partee系统转换规则的句法操作F101可从主动句“Mary loves John”计算得到被动句“John is loved by Mary”。主动句“Mary loves John”的范畴指派如上述,给其词条指派的范畴排列为:np1·(np1s)/np2·np2。而经F101运算后获得的被动句,给其中的词条指派的范畴系列是:这些范畴的逐级运算最后获得的也应是范畴s。例如被动句“John is loved by Mary”的情况:np2·(np2(s/np1))/(np2(s/np1))·np2(s/np1)·np1/np1· np1。我们的任务是从主动句的范畴指派系列推出被动句的范畴指派系列,即证明:
(1)np1·(np1s)/np2·np2→np2·(np2(s/np1))/(np2(s/np1))·np2(s/np1)·np1/np1·np1
简言之,就是证明:
(2)np1·(np1s)/np2·np2→np2·np2(s/np1)·np1
是否是范畴类型逻辑中可推出的定理①证明了(2),根据X/X·X跟X的互换,就证明了(1)。。概括来说,就是证明形如A·(AB)/C·C→C·C(B/A)·A的公式是否是CTL的LP系统的定理。
证明:
(1)(AB)/C→(AB)/C(A1等同公理)
(2)((AB)/C)→(AB)(由(1)依据R3规则)
(3)A·(((AB)/C)·C)→B(由(2)依据R4规则)
(4)(C·((AB)/C))·A→B(由(2)反复交叉使用A2和A3)
(5)C·((AB)/C)→B/A(由(4)依据R1)
(6)(AB)/C→C(B/A)(由(5)依据R2)
(7)A·(AB)/C·C→A·C(B/A)·C(两次运用单调律)
(8)A·(AB)/C·C→C·C(B/A)·A(对后件反复交叉使用A2和A3)
可见,A·(AB)/C·C→C·C(B/A)·A是范畴类型逻辑LP系统的定理,即(2)乃至(1)成立,表明蒙太格语法的被动转换规则符合范畴语法的规律,具有范畴语法的依据。
三、结语
本文通过Partee关于结构被动句的转换规则的考察,分析了蒙太格语法的转换思想。从新的视角探讨MG扩展的转换规则中的句法操作的范畴语法依据。这个工作采用了范畴语法的最新版本——范畴类型逻辑CTL所提供的工具,如交换的结构规则、结合的结构规则以及单调等规则。最终得出结论:MG是CG的发展阶段,不仅生成核心句的句法规则遵循范畴语法的函项应用原则,刻画转换思想的扩展规则也具有范畴语法的可计算依据,MG的两大类句法规则都可以作为自然语言信息处理的指导理论。
[1]邹崇理.自然语言逻辑研究[M].北京:北京大学出版社,2000.
[2]Barbara H.Partee.Montague Grammar[M].New York:Academic Press,1976.
[3]Yehoshua Bar Hillel,Chaim Gaifman,Eli Shamir.On categorical and phrase structure grammars[EB].Bulletin of the Research Council of Israel,1960,9F:1-16.
[4]邹崇理.自然语言逻辑的多元化发展及对信息科学的影响[J].哲学研究,2001,(1).
[5]Kosta Došen,Peter Schroeder-Heister.Substructural Logics(Studies in Logic and Computation)[M].USA:Oxford University Press,1994.
[6]邹崇理.范畴类型逻辑[M].北京:中国社会科学出版社,2008.
[7]章振邦.新编英语语法教程[M].上海:上海外语教育出版社,1992.
[8]吴平.汉语特殊句式的事件语义分析与计算[M].北京:中国社会科学出版社,2009.
[责任编辑:熊显长]
B81
A
1001-4799(2014)06-0057-05
2014-05-10
国家社会科学基金重大资助项目:10&ZD073
崔佳悦(1986-),女,河北唐山人,中国社会科学院研究生院2012级博士研究生;邹崇理(1953-),男,四川成都人,中国社会科学院哲学研究所研究员、博士生导师,主要从事自然语言逻辑研究。

