中心主子阵约束下矩阵方程AX=B的双对称解*

赵丽君

（台州学院 数学与信息工程学院，浙江 临海 317000）

中心主子阵约束下矩阵方程AX=B的双对称解*

赵丽君

（台州学院 数学与信息工程学院，浙江 临海 317000）

中心主子阵是指划去周边相同的行和列所得的主子阵。从中心主子阵扩充到双对称矩阵是有效和自然的一种矩阵扩充。通过分析双对称矩阵以及中心主子阵的结构，不仅给出了方程AX=B在中心主子阵约束下有双对称解的充分必要条件，而且给出了通解的表达式。在此基础上，也给出了最佳逼近问题的解的表达式。

双对称矩阵；中心主子阵；线性约束

1 引言

令Rn×m表示全体n×m阶实矩阵集合，令AT，rank（A），A+，R（A）和N（A）分别表示矩阵A的转置，秩，Moore-penrose广义逆，列空间和零空间.I表示单位阵。‖A‖为矩阵的Frobenius范数.令BSRn×m表示所有n×n阶双对称矩阵的全体［1］，Ac（k）=（0，Ik，0）A（0，Ik，0）T表示矩阵A的k阶中心主子阵，即划去周边相同行和列所得的k阶主子阵［4］.A［k］=（0，Ik）A（0，Ik）T表示矩阵A的k阶逆序主子阵.

双对称矩阵在通信理论，工程和统计，数值分析理论等许多方面有着重要的应用.事实上，对称Toeplitz矩阵和对称Hankel就是两类典型的双对称矩阵.关于双对称矩阵的研究已经有很多很好的结果，例如［3，6］以及他们的参考文献.双对称矩阵由于其本身特殊的结构，考虑顺序主子阵约束问题是不合宜的，因为它破坏了原矩阵的双对称性.在中心主子阵约束下AX=B的双对称问题的提法显然要比在顺序主子阵约束下AX=B的双对称问题［2］的提法更加合理，因为它是根据双对称结构的特性提出来的，但至今没有文章有关这方面的研究，本文就这一问题进行讨论.

问题I.已知X，B∈Rn×m，A0∈Rk×k求A∈BSRn×n使得AX=B且Ac（k）=A0.

2 问题I的解

引理1［2］.A∈BSRn×n当且仅当存在A11∈BSR（n-r）×（n-r），A22∈BSRr×r使得

其中r=［n/2］表示不超过n/2的最大整数，且Dn是正交矩阵.

引理2［1］.令A∈BSRn×n具有（1）的形式，A0∈BSRn×n.若A0有分解式

其中A10，A20分别为k-t阶与t阶对称矩阵，则A0是A的中心主子阵，当且仅当A10=A11［k-t］，A20=A22［t］.

设X∈BSRn×m的奇异值分解为

其中U，V为正交矩阵。

引理3［3］.给定X，B∈Rn×m，且X的奇异值分解为（3），则方程AX=B有对称解的充要条件是XTB=BTX和BX+X=B，且通解为，其中G为对称矩阵.

引理4［5］.设X∈Rn×m的奇异值分解为（3），则方程XTCX=K有对称解的充要条件是KT=K，KX+X=K，且通解可表示为，其中C12是实矩阵，C22是对称矩阵.

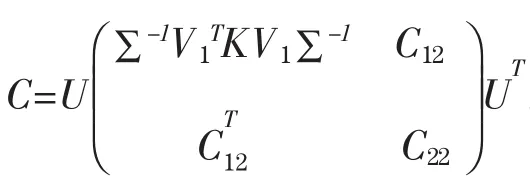
定理1.设X，B∈Rn×m，A0∈BSRk×k且A0如 （2）所示进行分块有如下分解），，其中X1，B1为前n-r行向量，X2，B2为后r行向量。并且有如下奇异值分解

则问题I有解的充要条件是

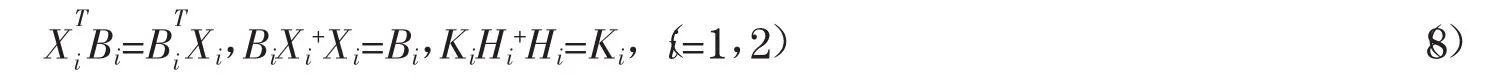
且解可表示为

其中E12，F12是任意的实矩阵，E22，F22是任意的对称矩阵.

且A11和A22满足

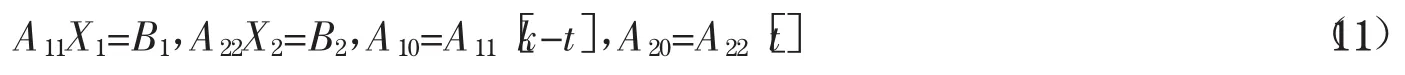
其中G1，G2是任意的对称矩阵.将（12）代入（11）,并注意到（5）（6）（7）式，则有，由引理4知，此式成立当且仅当，而由引理2和（7）式知Ki均是对称的，因此等价于（8），且G1和G2可表示为（10）.

3 问题II的解

当问题I有解时，容易验证解集合是闭凸集，因此，问题II存在唯一的最佳逼近解.下面我们给出最佳逼近解的具体表达式.

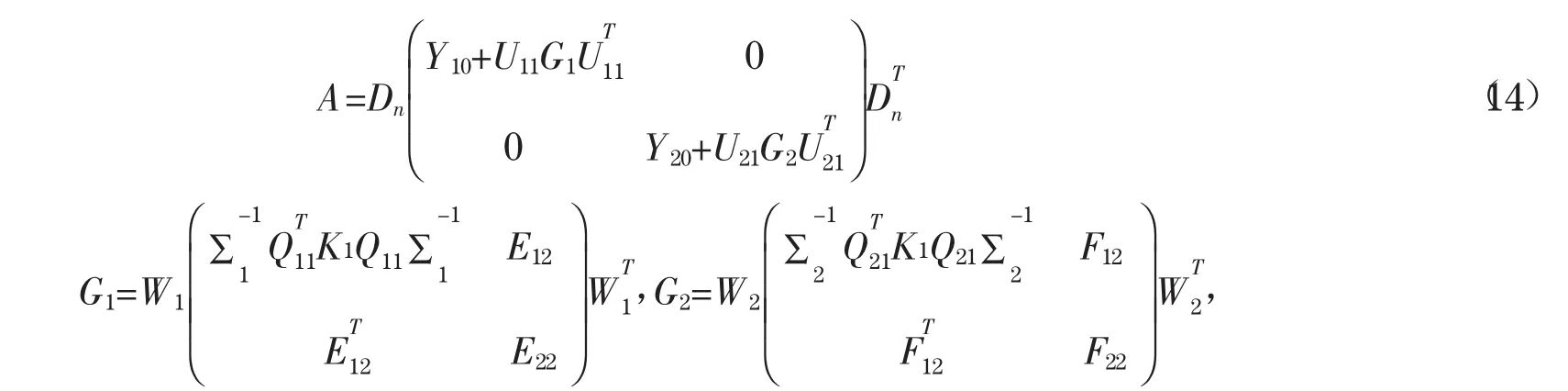
注意到W1是正交的，且是对称的，所以

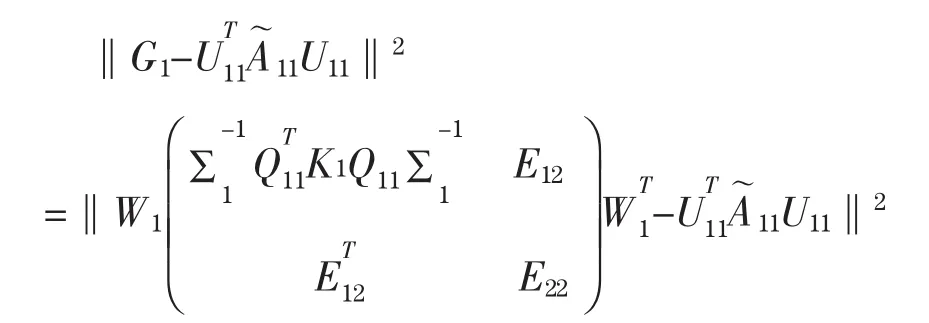
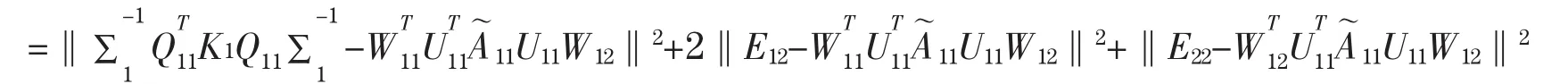
4 结束语

双对称矩阵由于本身的特殊结构，在中心主子阵约束条件下的双对称矩阵问题比在顺序主子阵约束下的双对称矩阵问题［2］的提法更加有效、自然和合理。因为顺序主子阵不具备双对称结构，而中心主子阵仍然具有双对称结构。根据双对称矩阵的特点，我们得到了双对称矩阵及其中心主子阵的降阶结构，并解决了双对称矩阵在中心主子阵约束下关于矩阵方程AX=B的约束问题，即得到了方程有解的充分必要条件以及解的表达形式。在此基础上，解决了相应的最佳逼近问题。

［1］Lijun Zhao, Xiyan Hu, Lei Zhang. Inverse eigenvalue problems for bisymmetric matrices under a central principal submatrix constraint［J］.Linear&Multilinear Algebra,2011,59（2）：117-128.

［2］Zhenyun Peng, Xiyan Hu, Lei Zhang. The inverse problem of bisymmetric matrices with a submatrix constraint［J］.Numerical Linear Algebra Applications,2004,11：59-73.

［3］孙继广.实对称矩阵两类逆特征值问题［J］.计算数学，1988，10（3）：282-290.

［4］Qingxinag Yin. Construction of real antisymmetric and bi-antisymmetric matrices with prescribed spectrum data［J］.Linear Algebra Applications,2004,389：95-106.

［5］Hua Dai,Lancaster Peter.Linear matrix equations from an inverse problem of vibration theory［J］.Linear Algebra Applications,1996,246：31-47.

Solutions to AX=B for Bisymmetric Matrices under a Central Principal Submatrix Constraint

ZHAO Li-jun

（School of Mathematics&Information Engineering,Taizhou University,Linhai 317000,China）

A central principal submatrix is a submatrix obtained by deleting the same number of rows and columns in edges of a matrix.This is a feasible and reasoned way to expand the submatrix to bisymmetric matrices. By means of the special structure of bisymmetric matrices and its central principal submatrix, this paper obtains not only necessary and sufficient conditions for the solvability of AX=B in bisymmetric matrices set under a central principal submatrix,but also the general representation of the solutions.Based on this,the expression of the solution for the corresponding optimal approximation problem is given.

bisymmetric matrix;central principal submatrix;linear constraint

10.13853/j.cnki.issn.1672-3708.2014.03.002

2014-02-28；

2014-03-26

国家自然科学基金委员会资助（11301107）。

赵丽君（1982- ），女，浙江台州人，讲师，博士，主要从事计算数学研究。