一种动刚度的测试方法及其在动平衡中的应用

鲁鹏，廖明夫，李明

（西北工业大学动力与能源学院，西安 710072）

动刚度是转子系统的重要参数之一，对研究转子系统的临界转速、振型、不平衡响应、传递特性等动力学特性，具有重要的价值[1]。转子系统结构状态上的变化在动刚度上将有直接反映。因此，动刚度测试对于研究转子结构与转子动力学之间的规律具有重要的应用意义[2]。但是如何获得转子动刚度曲线在国内外文献较少提及，Steve Sabin通过加载不平衡量方法简要介绍了测量动刚度的原理和获得转子动刚度的简略步骤[3]，并未对工程意义及应用进行讨论。近年来国内对动刚度的研究也主要是集中在支撑动刚度[4―7]。本文基于Jeffcott转子，利用转子不平衡激振力与转子不平衡响应的线性关系，建立了对转子系统动刚度的测试方法，测试结果综合考虑了转子—支承系统的装配工艺等因素对转子动刚度的影响，并基于动刚度提出了现场无试重动平衡方法，最后在转子实验器上进行了动平衡实验验证。

1 动刚度的测试方法

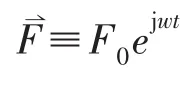
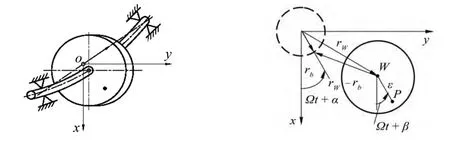
图1 Jeffcott转子模型

然而在动刚度的实际测量中还需考虑其他因素。如图1所示为一Jeffcott转子模型，由于材料不均匀、加工和装配误差等因素，存在一定的初始弯曲，相当于在转子上附加了不平衡量，破坏了转子原有的平衡状态，常常使得转子振动增大[2]。

通常并不能确切地知道转子系统的初始弯曲量，因此采用如下方法测动刚度，可以去除初始弯曲的影响：

（2）在转子的某个确定位置（相位为δ）加上一确定的不平衡量m，再次测出转子系统的振动位移响应；

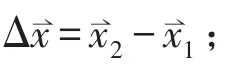
（4）计算不平衡量引起的不平衡激振力Δ=mrΩ2ejδ；

（5）利用步骤3和步骤4得到的振动位移响应Δ和不平衡力 Δ计算动刚度

通过以上步骤，可以测得转子系统在全转速下的不平衡响应，得到转子系统暂态过程的振动位移响应。不同转速下不平衡力的大小已知，就可以计算出整个工作转速范围内的动刚度幅频和相频曲线。

2 基于动刚度的无试重动平衡

基于动刚度的无试重动平衡是指在进行动平衡之前测得转子系统的动刚度曲线，在同类转子系统上进行动平衡时,直接利用已知的动刚度曲线计算配重，因而就省去了加试重的环节。

在线性条件假设下，当转速为Ω时转子系统动刚度的表达式为[8]

而影响系数的矢量表达式为[2]

由此可得出影响系数与动刚度的关系式为

影响系数法的平衡条件为[2]

平衡条件为

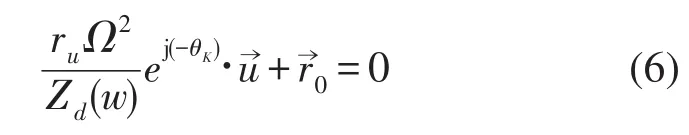
其中ru为测试动刚度时添加不平衡量的作用半径，为平衡校正量，为初始振动量，Zd(w)为动刚度矢量的幅值，θk为动刚度矢量的相位。

转子在工作转速下稳态运行时，转子的结构状态和性能将在一段时间内基本稳定不变[9]，即转子的动刚度基本不变。因此，可以考虑在转子第一次运行或者大修期间，较为准确地测得转子动刚度的幅频曲线和相频曲线，并将其存储到计算机中，当进行转子动平衡时再由软件调出。当发现转子振动异常须进行动平衡时，则采集一组初始振动信号，和调出存储的动刚度一起代入到式(6)中，即可求得校正质量但所选取的平衡面和测点与上次测得转子的动刚度时所选取的平衡面和测点需保持一致，否则计算结果不正确。

此外，在进行单面动平衡时，如果转子的振动仍未降低到允许的范围，则加校正质量的过程本身可以看作是一次加试重的过程，重新计算动刚度。如果发现新的动刚度与之前存在明显差异，则说明转子系统的结构状态发生了变化[9]。

3 实验验证

Jeffcott转子是个非常简化的模型，但它包含了一些转子的基本特征。通过对Jeffcott转子的研究，可以得到转子动力学重要典型现象的定性研究[10]。

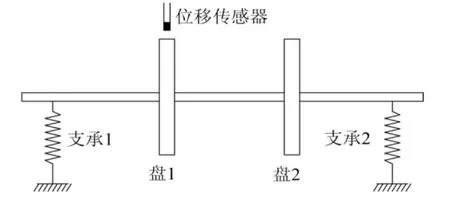
图2 转子实验器的简化模型

基于Jeffcott转子提出的不平衡力与响应之间的动刚度测试方法，也适用于双盘单转子实验器。利用双盘单转子实验器，对转子系统的动刚度进行测试并将得到的动刚度进行无试重动平衡实验，图2所示为实验器简化模型。在联轴器水平方向安装光电传感器，确保整周期采集数据，在盘处支座水平和垂直方向上呈90°分别安装电涡流位移传感器，用于测量振动信号。利用西北工业大学中德所研制的航空发动机状态检测与故障诊断系统，测量水平和垂直方向的振动数据，根据动刚度测试方法获得转子系统动刚度，并进行无试重动平衡实验。

3.1 转子实验器动刚度测试实验

使转子运行，测出整个工作范围的不平衡响应的振动位移幅频和相频曲线，如图3所示。在转子实验器的盘上0°位置半径为250 mm处加上一质量为m=3 g的不平衡量，测其整个工作范围的振动位移幅频和相频曲线，如图4所示。

图3 无调整状态下的振动响应

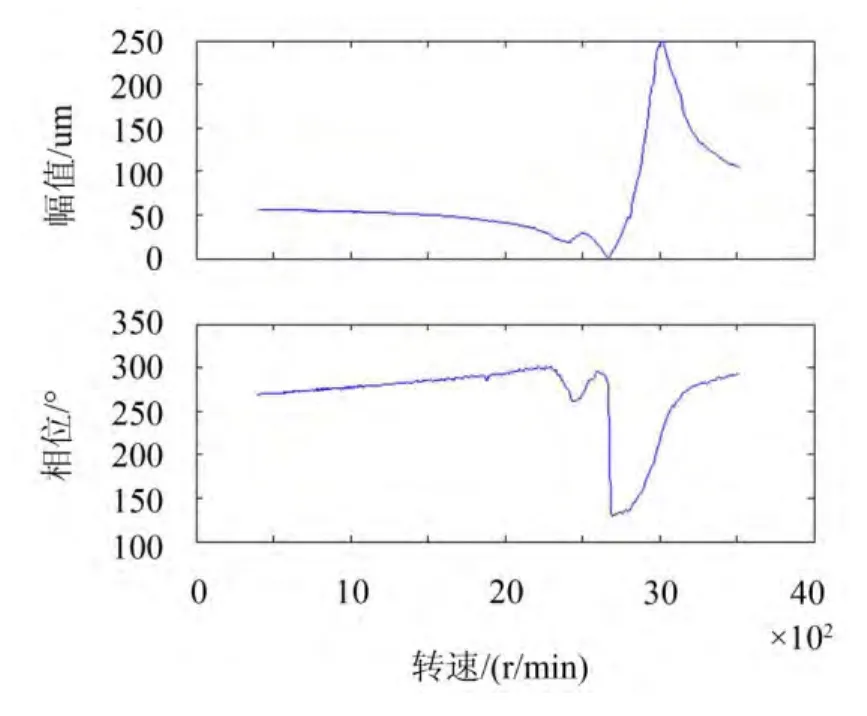
图4 加不平衡量状态下的振动响应

所得的动刚度的实部与虚部如下图5所示。

根据文献[6]和文献[3]可知，动刚度不仅与结构的内部属性有关，如质量m，阻尼c，静刚度k，同时还与转速Ω有关，其线性条件假设下的表达式为

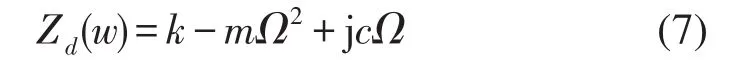
由于在低转速下，平衡前后的不平衡响应量Δx相差不大，由步骤（5）中的公式可知，低速段的动刚度计算数值不稳定，曲线比较振荡。将测得的振动数据实部用最小二乘法拟合，得到的实部拟合曲线如图6所示。

图680 N∙m时动刚度实部最小二乘法拟合曲线

由图6可知，拟合曲线与Y轴的交点为1.616×106N/m，与测得的转子支承系统的静刚度基本吻合；曲线与X轴的交点为2 946 r/min，与系统的临界转速基本相同。与文献[3]中图相比，实部曲线变化趋势与节点基本吻合，所以这种动刚度的测量方法是有效可行的。然而文献是基于单盘单转子、线性粘性阻尼力模型，但实测的虚部变化曲线表明文献中采用的线性阻尼力模型和真实的阻尼力不一致，真实阻尼力由实际的诸多外在因素决定，所以与文献[3]中给出简单的线性阻尼力曲线不符，但这并不影响对转子进行动平衡。

为验证转子结构状态改变将引起动刚度的变化，改变转子支承系统的装配参数，将轴承的锁紧螺母的力矩由80 N∙m改变到60 N∙m时，测得的动刚度曲线用最小二乘法拟合如图7所示。

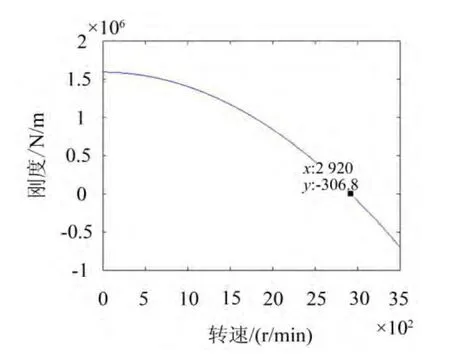
图760 N∙m时动刚度实部最小二乘法拟合曲线

转子系统的静刚度由1.616×106N/m变为1.588×106N/m，临界转速降到2 920 r/min。说明当系统结构状态发生变化时，动刚度随之发生变化，因此，用于进行转子动平衡的动刚度数据需随之更新。同时根据动刚度的变化也可检验转子支承系统的装配工艺是否与之前一致。

通过对图5所测数据进行复数运算，可得到全转速下动刚度向量的幅频曲线和相频曲线如下图8所示。

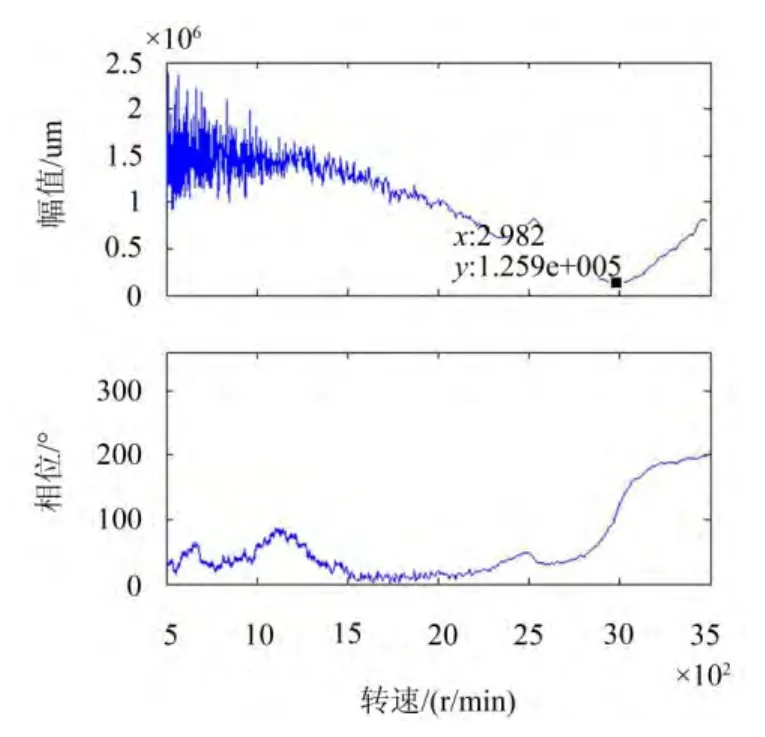
图8 动刚度幅频曲线和相频曲线

因为通常对转子系统动平衡都是在较高转速下进行，所以在低速段测得动刚度振荡曲线将不再使用。将测到的动刚度幅频曲线和相频曲线存储到计算机中，以备计算动平衡时调用。

3.2 转子实验器动平衡实验

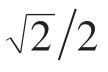
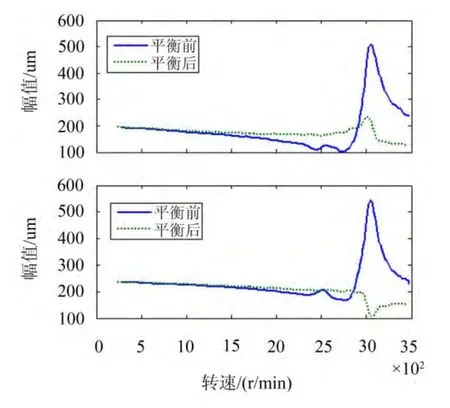
图9 暂态响应幅频曲线

当转速为3 000 r/min时,由图9实线的幅频曲线可得盘垂直的振动量413∠294°，水平的振动量448∠306°。从动刚度幅频曲线和相频曲线（如图7）可得到动刚度幅值和相位分别为1.259×105N/m和111°，ru为250 mm。

由式(6)可计算得到应加的配重质量约为2.1 g，相位为45°。考虑到盘上的配重加装位置，实际上将2 g的配重加在了40°的位置上。再次运行转子，测得不平衡响应的暂态响应幅频曲线如图9虚线所示。

如图3所示，转子系统的初始不平衡量幅值为52 μm，由图9实、虚线比较可得出：在转速为3 000 r/min时，盘垂直的振动位移幅值在平衡之后减为231.7 μm，盘水平的振动位移减为169 μm，减去初始不平衡量的幅值，垂直方向振动量降低了50.4%，水平方向振动量降低了70.4%，取得了明显效果。

4 结语

建立了基于转子不平衡激振力与转子不平衡响应的线性关系的转子—支承系统动刚度实验测试方法，并将其应用于现场无试重动平衡，并得到如下结论：

（1）建立的转子—支承系统动刚度实验测试方法是实用可行的；

（2）基于转子动刚度的现场无试重动平衡是可行的，可作为转子现场动平衡的有效手段；

（3）建立的转子动刚度方法还可用于转子动力学设计的验证和检验每次转子—支承系统的装配工艺是否一致。

[1]张大义，母国新，洪杰.航空发动机转子支承系统刚度计算中的几个问题[J].战术导弹技术，2005，5(2)：20-23.

[2]廖明夫.转子动力学基础[M].西北工业大学出版社，2000.

[3]Steve Sabin.Understanding and using dynamic stiffnessa tutorial[J].ORBIT,2000(SecondQuarter):44-54.

[4]赵文涛，陈果，李琼，杨飞益.航空发动机机匣支承动刚度有限元计算及验证[J].航空计算技术，2011，9.

[5]杜兆刚，张艳春，刘少权.MS9001E燃气轮机轴承支座结构动刚度测试研究[J].燃气轮机技术，2010，3.

[6]石清鑫，袁奇，胡永康.250 t高速动平衡机摆架的动刚度分析[J].机械工程学报，2011，47(1).

[7]韩余才，刘胜军.汽轮发电机组动平衡的等效动刚度系数方法[J].中国电机工程学报，1997，17(1).

[8]方同，薛璞.振动理论及应用[M].西北工业大学出版社，2010.

[9]王四季，廖明夫.转子现场动平衡技术研究[J].机械科学与技术，2005，24(12)：1510-1514.

[10]Giancarlo Genta.Dynamics of rotating systems[M].Springer Verlag,2005-4.

[11王维民，高金吉，江志农，李燕.旋转机械无试重现场动平衡原理与应用[J].振动与冲击，2010，29(2)：212-215.

[12]王四季，廖明夫.航空发动机柔性转子动平衡方法[J].噪声与振动控制，2011，31(6).

[13]王勃，李光辉，廖明夫，王四季.某小型涡扇发动机柔性转子高速动平衡试验研究[J].噪声与振动控制，2008，28(6).