浅谈大学物理学习过程中应重视的几个要点

古丽姗

(昌吉学院 物理系，新疆 昌吉 831100)

大学物理是物理学专业和工科各专业的必修课，是培养和提高学生科学素质、科学思维方法和科学研究能力的重要基础课。 由于大学物理和中学物理在教学方法、学习方法等各方面的许多不同，对已习惯于中学物理的教学方法和学习方法、已经形成了一定的思维定势的大学物理初学者来讲，感到无法适应。在学习过程中，大多数学生只习惯于把中学的思维、中学的方法生搬硬套到新的物理情境中来，不善于变换认识问题的角度，也不善于改变解决问题的方式，使得本该有助于自己学习大学物理所具备的中学物理基础知识，不但没有利于大学物理的学习，却给学习带来了一定的负面影响，甚至一些自认为中学物理课程学的很好的学生，在学习大学物理过程中觉得自己都不会处理问题了，感到困惑、茫然。 究其原因，重要的还是对大学物理学习中应该重视的一些要点没有引起足够的重视，如何使学生尽快适应大学物理教学和学习特点， 尽快地从中学物理过渡到大学物理的学习，渡过学习大学物理的难关，是每个教大学物理课程的教师和学习大学物理的学生面临并需要亟待解决的问题。

1 重视高等数学知识在大学物理学习过程中的重要性

高等数学是大学物理学习的重要工具，学好大学物理必须要有一定的高等数学基础。 大学物理学习中常用的高等数学知识有矢量代数、微积分和建立的数学模型，在本文中，就矢量代数、微积分知识在大学物理学习中的重要性谈谈自己的认识。

1.1 例谈矢量代数在大学物理学习过程中的重要性

对于理工科学生来说，大学物理中所用到的高等数学知识其实是很简单的一部分，物理难其实不在于计算，而是在于对问题的分析。在大学物理中大多数的物理量都是用矢量表示的,而中学物理中并没有涉及过矢量的概念。 矢量的加减与乘法和标量是不同的，但是不少学生在学习中不适应这种变化，还停留在用初等数学来处理物理问题的水平上，往往不能正确地用矢量来表示和分析问题，而且还经常把矢量当标量等，这是最普遍犯的一个错误。如何避免发生这样的错误呢？我认为首先要学会把物理量的矢量放到适当的坐标系中进行分析，如直角坐标系，平面极坐标系，自然坐标系等。但同一物理量在不同的坐标系中的形式也是不一样的，坐标系的选择，依据所讨论问题的简便而定，所以在具体计算物理量的时候，需要建立适当的坐标系，想方设法将物理量的矢量式转换成标量式， 这样才会使计算变得十分简单。其次要注意大学物理教材中物理量及其相关规律的矢量表达式。一般教材中是矢量的物理量以及相关规律的印刷体均是用黑体字母表示的,而手写体用在字母正上方加箭头的方法来表示。 在手写体表示方法上,学生们往往看到书上矢量没有加箭头,自然而然在写作业时就忘了加,这是绝大多数学生最易犯的错误，尽管教师在教学过程中反复强调，但并没有引起学生的重视。 在大学物理学习中加强矢量代数运算训练,尤其是对概念、规律的矢量投影的训练是掌握好大学物理知识的关键性所在，必须要引起学生高度的重视才行。

众所周知牛顿力学常被人们称作矢量力学，它的运动学量以及动量、角动量规律都是以矢量形式出现的，具有普遍、简洁的特色。 下面就以牛顿力学中的一个典型例子为例不妨说明一下矢量代数在学习过程中的重要性：

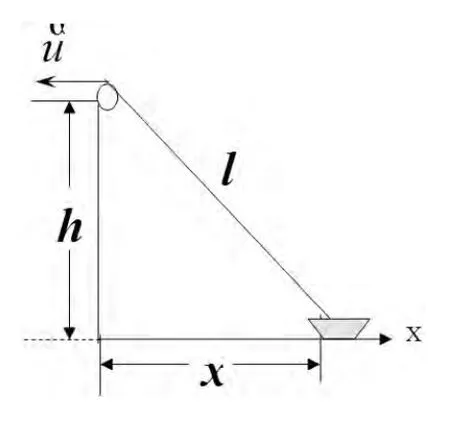
例如右图所示：通过绞车拉动湖中小船拉向岸边。 如果绞车以恒定的速率u 拉动纤绳, 绞车定滑轮离水面的高度为h, 要对小船的运动进行分析，亦即求小船向岸边移动的速度和加速度。 如果按图那样以岸边为原点沿湖面向右做x 轴，则小船的坐标为x，若将定滑轮至小船头这段绳子的长度设为l，则有不少学生对此式用求导的方法得到继续对t 求导，得小船的加速度为

仔细考虑一下，这种解法所得到的结果存在着问题。 如果v＞0，a＜0，小船应沿X 轴正方向做减速运动，然而现在小船却沿X 轴负方向运动。为什么解出的结果与实际不符呢？简单分析不难发现，采用这种解法的学生没有把物理量的矢量放到建立的坐标系中进行分析。如果解题过程中抓住速度的矢量性，根据所建立的坐标系就可以写出题中所涉及的所有速度在该坐标系中的表示， 如根据题中建立的坐标系，由于速度u 的大小为，方向与X 轴方向相反即其在该坐标系中的矢量表达式为：

这种解法所得到的结果v＜0，a＜0，沿X 轴负方向运动并且是加速运动，与实际相符，就不会存在问题了。 这样的例子很多，在此就不再一一例举了。

由此可见， 会把物理量的矢量放到适当的坐标系中进行分析，计算过程会更简单明了，也不会因为计算出的物理量前的符号问题而发生概念错误， 还能避免我们在解题时出现的随意增抹符号的概念错误。

1.2 例谈微积分在大学物理学习过程中的重要性

微积分知识是我们在大学物理学习过程中需要高度重视的另一个重要的数学工具。通过大学四年物理专业课程的学习我感受到大学物理不同于高中物理的重要的特点其实就是大学物理中公式的推导定量表示时广泛应用微分、积分的知识，而且有很多问题在处理中也都要用到微积分的方法。它可以将问题化繁为简、化难为易，可以帮助我们掌握概念的内涵,分析、解决问题；更重要的是能够帮助我们理解物理量微分形式的物理含义。微积分的分析方法已经成为解决大学物理问题的基本方法。因此，在大学物理的学习过程中我们要转变观念，学会用微积分思想去思考问题。

无限地分割复杂物理对象为无限小的物理对象,称为微分,每一个无限小的物理对象叫做微分(元)。 在微分范围内,抓住物理对象的主要矛盾而忽略次要矛盾, 即近似处理, 就能够把复杂物理对象近似成简单、基本、可以描述分析的物理对象，然后把无限多个微分的物理对象的描述分析集中起来,就是积分。 一般来说，推导公式或解题的关键就是要能找到所求物理量的微分表达式，并用已知条件表示出来，再求积分。 下面可以举例来说明：比如利用微积分的方法来推导我们早已熟悉的动量守恒定律，具体推到过程如下：

从动量守恒定律的推导过程可见，利用微积分思想方法不仅能使我们清楚了解到大学物理课程中的新任务，还能更清晰地了解规律的推理过程。

综上所述，用高等数学来理解和处理问题是大学物理给学生提出的一个新课题和基本要求。如果在学习大学物理过程中学生对这个问题不能给予足够的重视，不尽快予以突破，高等数学知识将成为他们大学物理学习道路上的一个最大的障碍。

2 重视大学物理教材和教法上的特点，初步把握大学物理学习要点

在知识上大学物理是中学物理的延伸和拓展而不是知识的重复。在教材和教法上独具自己的特点：

第一， 在教材上，大学物理教材注重理论上的分析、推理、论证，是用高等数学微积分思想方法与矢量代数描述分析物理问题。所以比较抽象，每章之后配有相应与该章节内容相关的习题以及与其他章节内容联系的综合题。 所以在大学物理的学习中，要求学生必须具有较强的自学能力， 克服自身在中学学习物理时对老师养成的依赖性，增强自身在学习过程中的自主性。使自己尽快适应大学物理教学和学习特点，从中学物理学习中快速过渡到大学物理的学习当中。

第二， 在教法上，大学物理教师要在短时间内讲授大量的物理知识，课堂主要以教师的讲解为主，几乎没有互动，例题也更关注物理过程的分析、定律的应用，而不是具体的计算过程。大学物理更强调更注重是培养学生科学系统的物理思维和方法,将自然科学上升到了更高的一个层次，而不像中学物理只强调要会做题就可以了。 这点与中学物理教学是完全不同的， 因此初学大学物理的学生必须要高度重视，在上课时要做好笔记，课后需花时间研读教材，加强复习，归纳、总结所学知识，做相关的练习时注重物理问题的过程分析，理清思路，在此基础上再选用合适的规律熟练解决问题。要求在解题过程中对写出的每一个方程或等式都要做出必要的文字说明即注明该方程或等式依据的是哪个规律，为什么要用这个规律等。而不是惯用中学模式，把物理题当成数学应用题来做， 整个解答过程只有几个干巴巴的式子，没有一个文字说明，即便出现错误还不能察觉是哪里出了问题。 下面举一个非常简单的实例来说明一下：

例如右图示一斜面，倾角为α，底边AB长为l=2.1m， 质量为m 的物体从斜面顶端由静止开始向下滑动， 斜面的摩擦因数为μ=0.14。 试问，当 α 为何值时，物体在斜面上下滑的时间最短?其数值为多少?

教师解法： 该物体的受力矢量图如图所示，取沿斜面为坐标轴Ox，原点 O 位于斜面顶点，则由牛顿第二定律有：

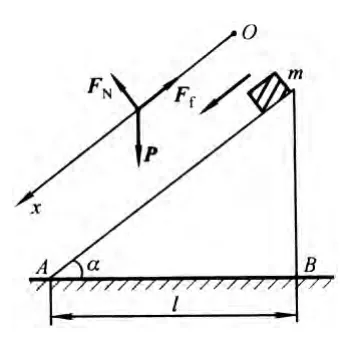
又物体在斜面上作匀变速直线运动，故有：

对（2）式进一步分析，不难知道，时间是的函数，所以为求物体在斜面上下滑的最短时间t，可令dt/dα=0，由式(2)有：

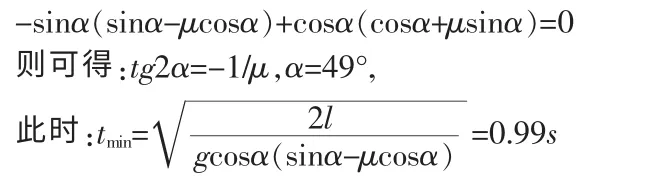
由过程分析可见，该题关键在列出动力学和运动学方程后，解出倾角与时间的函数关系α=f（t），然后运用对t 求极值的方法即可得出数值来。

3 结论

大学物理课程是高等院校理工科各专业学生的一门重要的基础课，其内容包括力学、热学、电磁学、波动光学、近代物理五部分。 该课程对学生的要求是：学好必要的物理知识，为今后的学习和工作打下坚实的物理基础， 通过该课程的学习培养科学的思维方法及分析问题、解决问题的能力。 由于大学物理较多地应用了高等数学知识,这和中学物理相比,是一个较高的梯度，因此初学大学物理的学生必须要摆脱中学的学习方法和学习习惯的束缚，形成良好的学习心态，并使自己较快适应大学物理学习的新要求， 从而使学习形成良性循环，这样才能学好大学物理。

［1］黎定国,等.大学物理中微积分思想和方法教学浅谈[J].大学物理,2005（12）.

［2］罗仁俊.关于大学物理与中学物理衔接问题的讨论[J].中山大学学报,2005（03）.

［3］郝会颖.大学物理教学改革的探索与实践[J].中国科技信,2008(06).

［4］张金平.高职大学物理课程教学探讨[J].新西部(下半月),2009(05).

［5］刘克哲,张承琚.物理学[M].4 版.高等教育出版社,2012.

［6］严国清,彭振生.例谈大学物理学习方法[J].宿州学院学报，2011（11）.