康复助力器吊臂的有限元分析
孙 泽 民,王 奥,杜 国 金,孙 秋 花,彭 彦 平
(大连工业大学 机械工程与自动化学院,辽宁 大连 116034)
0 引 言
康复助力器属于医疗康复器械的一种,由于它的实用性和灵活性,在国外已被广泛应用,其开发及应用具有理论及实际价值。作者设计研究一种可实现下肢的康复训练,以及辅助护理人员便捷移动患者这样双功能的轻便式康复助力器。它的主要功能之一是,患者可以在护理人员的牵引下方便地移动,减少人工搬移的不便性。它实现的功能之二是,使患者进行腿部的康复训练,以伺服电机的主动旋转带动患肢做被动的圆周蹬踏训练,患者也可以依靠自身的肌力,在没有电机的牵引下自主完成圆周蹬踏训练运动,从而使下肢关节运动机能逐渐得到恢复。
其中康复助力器吊臂梁是整机中的主要部件,患者的大部分重量由其承担,因此吊臂设计是否合理,直接影响着助力器的承载能力和整机的性能[1]。
如何在规定的变形和应力的约束条件下进行吊臂的设计计算,使得吊臂梁体积最小、材料最省,是设计中必须解决的问题。本文通过理论力学及有限元分析软件对吊臂梁进行设计分析,获得了理想的吊臂断面形状和结构尺寸,设计更为合理。
1 吊臂梁截面形状及截面面积的选择计算
1.1 设计分析
康复助力器机构原理简图如图1所示。受人体重力载荷作用的吊臂梁,在电动推杆推力T的作用下,可绕铰接点O在一定范围内作定轴转动,结合医用吊带及膝部固定架的支撑,可实现患者的安全起吊功能。
推力T在Y方向的分量Ty对吊臂梁的升降起主要作用。因为起吊载荷所受的重力方向竖直向下,当吊臂长度方向与载荷重力方向垂直时,吊臂各横截面的弯矩最大,即在等截面情况下所受应力最大,所以取吊臂与水平成0°时为研究状态,对吊臂的截面形状及截面面积进行设计计算。
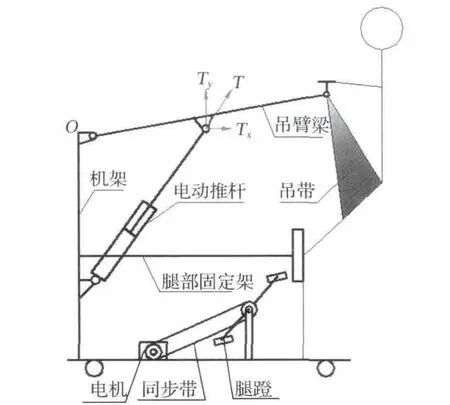
图1 机构原理简图Fig.1 Principle diagram of mechanism
此时吊臂梁可简化为图2所示端部受集中载荷G作用的外伸梁。
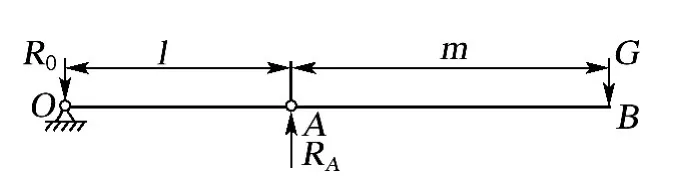
图2 结构简化受力图Fig.2 Force diagram of simplified structure
按实际工作需要及人体重力载荷大小,取臂长L=600mm。对于中间铰接点位置的确定,综合考虑电动推杆的额定推力和额定行程的大小,并结合在吊车起重吊臂的一般设计中,一般取L/3<l<L/2,取其平均值得:
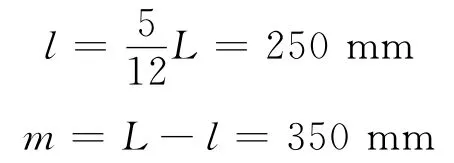
1.2 力学分析及计算
根据设计要求,吊臂工作时所承受的最大载荷为100kg,但吊臂在起降瞬间,载荷会对承载结构产生附加的动载荷作用,在考虑这种情况的载荷组合时,应将起升载荷乘以大于1的起升载荷动荷系数φ2,取φ2=1.25。
在一般梁的机械设计中,梁的自重小于其承受的载荷,为简化计算,可先按略去吊臂的自重进行处理。
由静力平衡方程求出吊臂梁的支座反力。
RA=GL/l=2 940N
RO=Gm/l=1 715N
吊臂梁的弯矩图如图3所示。
由图3可知,最大弯矩在铰接点A处,即
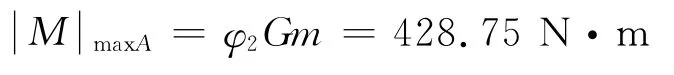
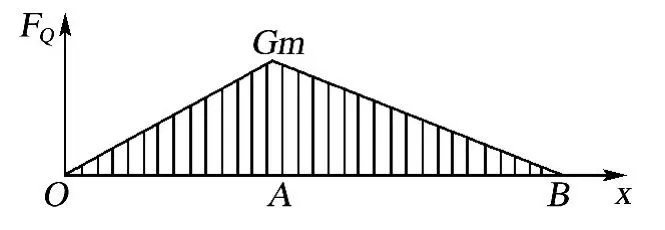
图3 弯矩图Fig.3 Bending moment diagram
1.3 截面选择计算
弯曲正应力是控制弯曲强度的主要因素,为保证吊臂梁在载荷作用下能安全可靠地工作,并考虑到必要的强度储备,利用弯曲正应力强度条件,对吊臂进行截面设计,即

式中:σmax为最大工作应力,MPa;Mmax为最大弯矩,N·m;WZ为抗弯截面系数,cm3;[σ]为材料许用应力,取157 MPa[2]。
由式(1)得
WZ≥Mmax/[σ]
代入数据得
WZ≥428.78N/157=2.731cm3
从此条件可以看出,梁所能承受的最大弯矩Mmax与抗弯截面系数WZ成正比。WZ不但和截面尺寸有关,且与截面形状有关。为了减少吊臂梁材料消耗,减轻自重,应选用抗弯模量WZ较大而截面面积较小的截面形状,即一般所谓的合理截面形状[2]。
由梁受弯截面的正应力分布规律可知,横截面上任意一点处的正应力与该点到中性轴的距离成正比,而在距中性轴为y的同一横线上的各点处的正应力均相等,中性轴的正应力为0[3]。所以弯曲时在梁横截面上离中性轴越远,正应力越大。为了充分利用材料,应尽可能地把材料放置到离中性轴较远的地方。
由此可见,同一截面形状的受弯曲梁,空心梁比实心梁更能充分发挥其材料性能,而且减轻了梁的质量,节约材料。
在通用的方形钢、矩形钢、圆形钢3种不同截面型钢梁中,以满足WZ≥2.731cm3为极值条件,选得截面面积最小,单位质量最轻的3种常用型钢的最佳结果,如表1所示[4]。
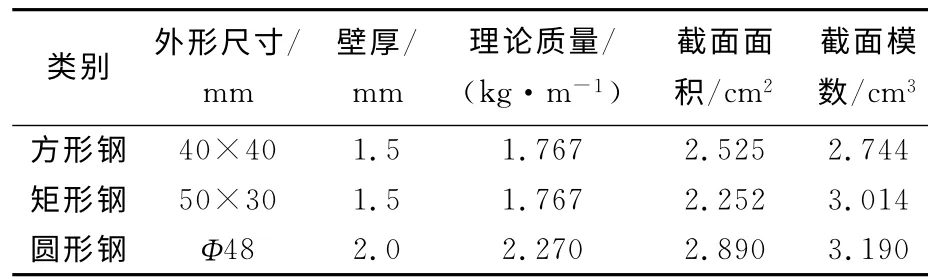
表1 型钢表Tab.1 Steel table
由表1比较可知,矩形钢在3种型钢中性能最突出,所以吊臂选取截面为矩形的空心型钢梁。
2 吊臂梁的强度、刚度分析
采用功能强大的有限元软件ANSYS为截面形状为矩形的康复助力器吊臂梁进行强度及刚度分析,并结合梁的自重,对结果进行校核与验证。
2.1 有限元模型的建立
建立吊臂梁的有限元模型,是进行有限元分析的前提和基础。模型建立的基本原则是既要如实反映结构的主要特征,又要尽量降低模型的复杂程度,以保证分析结果既有较高的计算精度,又能降低计算工作量,以节约计算所需的资源[5]。
考虑到吊臂梁模型的结构尺寸在长度上远远大于其宽度和厚度,为了提高有限元分析效率,在ANSYS中利用自定义截面梁单元直接建立模型进行有限元计算,这样在提高效率的同时又能简化3D 模型的建模过程和求解步骤。
2.1.1 模型的建立
在ANSYS环境下,通过表2 创建3 个关键点,其中连接关键点1、2作为梁的轴线,关键点3作为方向关键点。
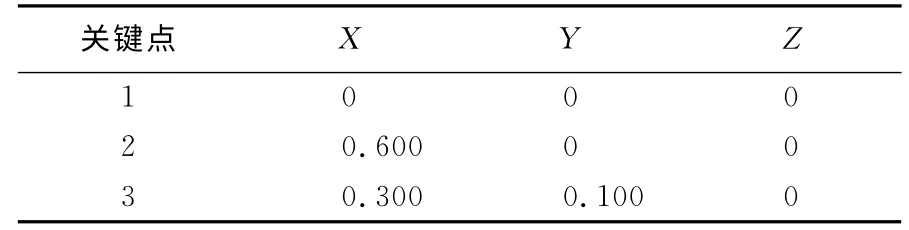
表2 关键点编号及坐标Tab.2 Number of key point and coordinates
2.1.2 单元类型的选择
梁单元是有限元法进行梁柱体系分析时最常用的单元。对于不同梁结构,ANSYS提供了不同的梁单元。实验采用基于Timoshenko梁理论的三维二次有限应变梁单元BEAM189。BEAM189适合于细长梁或适度深梁的计算分析,并考虑剪切变形的影响,其使用及后处理比起传统的梁单元更加直观方便,具有更广泛的适用性。
2.1.3 定义材料属性
材料的弹性模量设置为2×1011Pa,泊松比为0.3,密度为7 850kg/m3。
2.1.4 定义单元截面
通过对应的GUI流程,参考表1中的数据为梁单元指定矩形截面的相关参数,所得矩形截面图如图4所示。
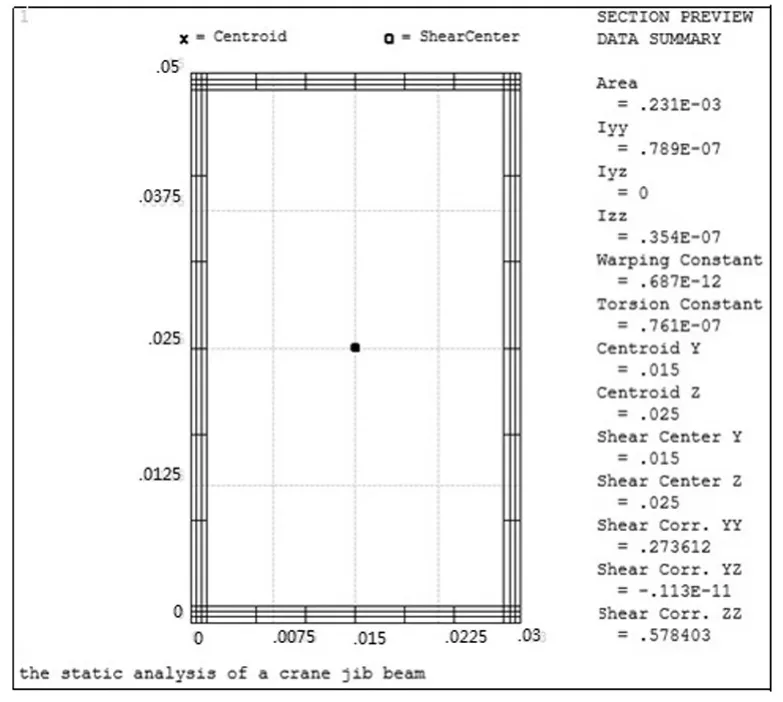
图4 梁单元截面Fig.4 Cross-section of beam
由图4可得到程序自动计算的梁截面的几何参数,包括面积、惯性矩、重心以及剪切中心位置等。
2.1.5 划分网格
从理论上来说,网格划分得越细,越符合实际,结果越可靠,但网格划分得过密,会不可避免地增加运算量和运算时间,所以综合考虑计算精度和运算速度,在分析时,将网格划分份数设置为24。同时为梁单元分配相应的线单元属性参数及截面属性参数。
最终生成有限元模型如图5所示。
图5 吊臂梁有限元模型Fig.5 Finite element model of hoisting beam
2.2 加载及约束处理
载荷组合:吊重(考虑动载系数)和吊臂自重。对于吊臂自重的处理,可在前处理模块中对应输入吊臂材料的密度和重力加速度,程序便根据单元类型、截面参数自行进行计算。对于吊重载荷的施加,可认为在吊臂梁末端施加一个等效集中力,力的大小为患者重力与动载荷系数的乘积。
约束处理:吊臂梁尾部与机架铰接处,约束3个方向平移自由度(UX,UY,UZ)和2个方向的转动自由度(RX,RY),释放绕销轴中心回转的转动自由度RZ。中间的铰接位置做同样处理。
2.3 计算结果处理及分析
2.3.1 强度校核
图6显示了载荷作用后的应力变化情况。从图中可以看出,最大应力出现在梁的下表面位于中间铰接的位置,在变形过程中梁的中性面以上受拉,中性面以下受压。因为吊臂梁采用的金属材料为Q235钢,其许用应力[σ]=157 MPa,由应力云图可知,此工况下的最大Von Mises等效应力为136MPa,小于材料的许用应力。可见,此梁结构在承受给定最大载荷情况下,其强度满足要求。
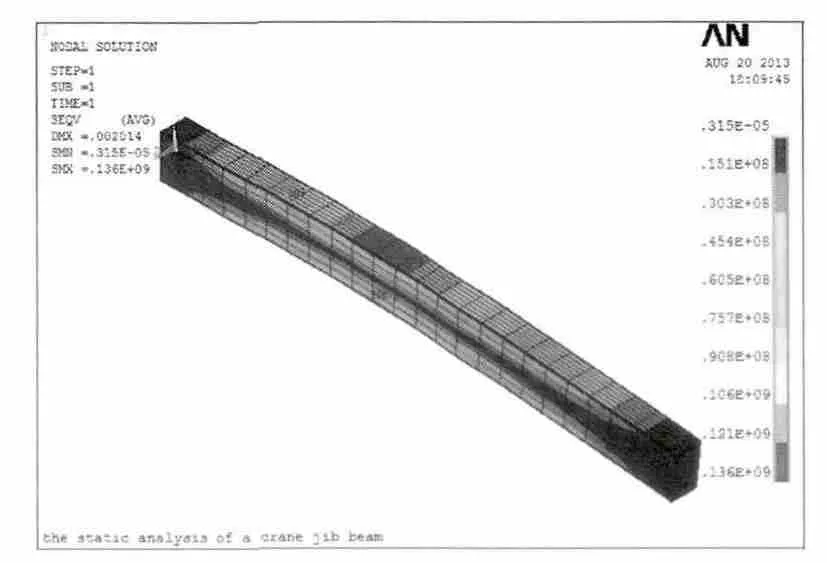
图6 吊臂梁应力云图Fig.6 The stress nephogram of crane jib beam
2.3.2 刚度校核及变形分析
为了保证机器的正常工作和梁的安全,在按强度条件选择了梁的截面后,往往还要进行刚度校核。需要把梁的变形限制在一定的范围内,即满足刚度条件:

式中:[y]为梁的许用挠度值,mm。
在载荷作用下,吊臂梁发生变形如图8所示,最大变形量出现在集中载荷作用处,也就是承受载荷的位置,其值Δmax=2.014mm。
结果表明,受载前后吊臂梁变形量很小,对整机的稳定性几乎无影响,因此吊臂的选材及尺寸符合设计要求。
综上分析,基于ANSYS有限元分析结果合理可靠。
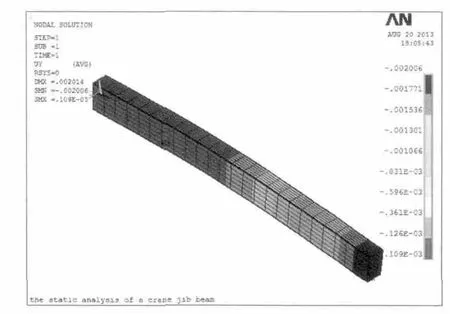
图7 Y 方向位移场分布等值线图Fig.7 Contour of Y-direction displacement field distribution
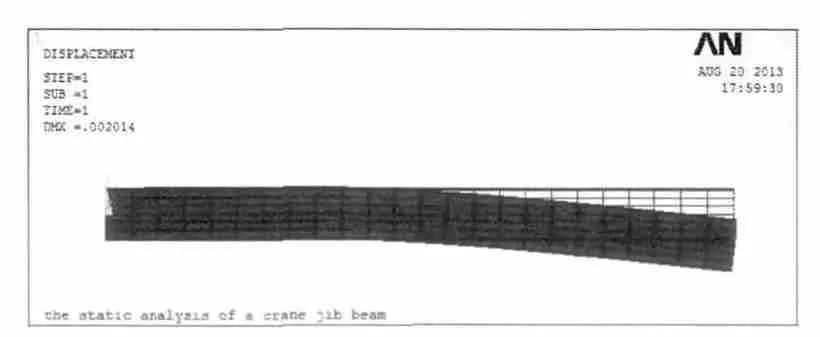
图8 吊臂梁变形图Fig.8 Deformed shape diagram of crane jib beam
3 结 论
通过理论力学的计算和有限元分析,对康复助力器吊臂进行了设计分析。结果表明,所设计的吊臂梁在满足使用要求的情况下,其质量最轻,所用材料最省,对此类康复助力器的技术提升起了重要的作用。
从应力和变形云图可以看出,吊臂梁在承载外力时,其最大应力及最大变形发生的部位,为吊臂结构的加工生产提供了工艺指导。
[1]马志宇.汽车起重机箱形伸缩臂的有限元分析与研究[D].贵州:贵州大学,2009:1-20.
[2]齐威,林巍.工程力学(I)[M].大连:大连理工大学出版社,2008:252.
[3]杨青,赵吉坤.梁截面优化对工程造价的影响分析[J].建筑技术,2010,41(10):942-945.
[4]成大先.机械设计手册:第3卷[M].4版.北京:化学工业出版社,2002:131-139.
[5]杨晶,李卫民,刘玉浩.汽车起重机吊臂的有限元分析[J].辽宁工学院学报,2007,27(3):195-197.

