具有参数不确定性的火炮弹药协调器定位精度优化

高学星，苏哲子，孙华刚，侯保林

(1.南京理工大学 机械工程学院，江苏 南京210094;2.中国兵器科学研究院，北京100089;3.总装备部 军械技术研究所，河北 石家庄050000)

0 引言

现代自行火炮对于火力、射速、机动性、战场生存能力、信息化水平、人机工程等性能有着苛刻的要求，因此系统复杂，存在故障频发的问题。典型故障之一就是弹药自动装填系统协调定位失效。

火炮的弹药自动装填系统旨在取代火炮的弹药选取、放置、传递、管理、输入炮膛等动作的人工操作并保证火炮高效、可靠射击。

弹药自动装填系统的协调器(见图1)用于接收弹仓内被推弹器所推送出来的弹丸，然后将该弹丸传送到输弹线上由输弹机输弹入膛后协调器再返回原位。协调器由两个串励式直流电机并联驱动，减速传动部分包括两级直齿轮传动和一级蜗轮蜗杆传动组成，其中蜗轮与耳轴固联。由平衡油缸和蓄能器等组成的小平衡机，用于平衡协调器的重力矩，减小驱动电机的负载，支撑协调器平稳运动。协调器与托架之间有角度传感器，用于提供协调器相对于起落部分的角度信号，使协调器转至正确位置［1］。

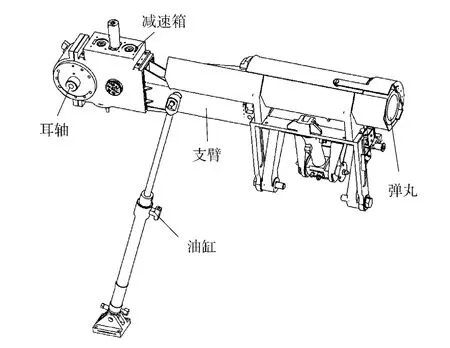
图1 协调器Fig.1 Shell transfer arm

协调器定位精度是一个受控、高速的机电系统动态过程结果，其可靠性受炮塔扰动、传动摩擦系数、液压系统性能、驱动电压等多个不确定性因素影响。在计算定位精度可靠性时，其极限状态函数是定位误差ε(X)=ε0，其中X =(x1，x2，…，xn)是不确定性变量，ε0是限定定位失效的某个确定值。ε(X)=ε0的显式表达式是无法直接求解获得的，通常可以使用响应面法［2］、Kriging 法［3］、神经网络法［4］等获得近似的极限状态函数，再进行可靠度或者可靠性参数的求解，最终计算得到的可靠性是有误差的，同时需要一定的计算时间。

如果进行基于可靠性的优化设计，每次改变设计变量时都需要重新计算可靠性，迭代过程中的反复计算可靠性，会造成令人难以接受的计算时间花费［5］。实际上，优化过程中的具体可靠性数值并不完全可信，只要保证优化的趋势是正确的，同样可以实现提高可靠性的目的。

本文避开优化过程中的可靠性计算，对不确定性变量进行空间转换，根据标准空间中采样点到均值点的距离来计算误差权值，在Simulink 中建立动力学和控制模型并对采样点进行仿真以获得定位误差，将定位误差的加权和作为优化过程的性能参数，并采用粒子群优化算法对该性能参数进行优化。

1 协调器建模

1.1 动力学建模

协调器支臂的受力分析如图2 所示。

图2 支臂受力分析Fig.2 Dynamic analysis of arm

影响协调器支臂转动的主要力有支臂自身重力m1g，炮塔垂直方向振动等效为支臂惯性力变化βm1g，小平衡机的支撑力F1，蜗杆对支臂的沿蜗杆轴向作用力F2. 由刚体定轴转动动力学:

对蜗杆进行受力分析(见图3)，在其轴向方向有

图3 蜗杆受力分析示意图Fig.3 Dynamic analysis of worm

旋转运动方程:

(2)式和(3)式中:m2为蜗杆质量;l2为蜗杆轴线到耳轴的距离(见图1);Fa、Ft，Ffa、Fft分别为接触压力的轴向分力、周向分力，摩擦力的轴向分力、周向分力:Fa=Fncos αncos γ，Ft=Fncos αnsin γ，Fft=cos γ=μFncos γ，Ffa=Ffsin γ =μFnsin γ，αn为压力角，γ 为导程角，Fn为蜗轮蜗杆啮合正压力，μ 为摩擦系数;Tb为电磁制动器输出力矩;r2为蜗杆分度圆半径;

为前级齿轮作用于蜗杆的转矩，T 为电机的输出转矩，n1、n2、n3为减速箱的三级传动比，其中蜗轮蜗杆的传动比n3=60，Tf为前两级齿轮的传动阻力矩。

将以上方程进行整理，在Simulink 中建立仿真模型。

1.2 控制系统建模

驱动单机使用的是两个串励式直流电机，相关的动态方程［6］有

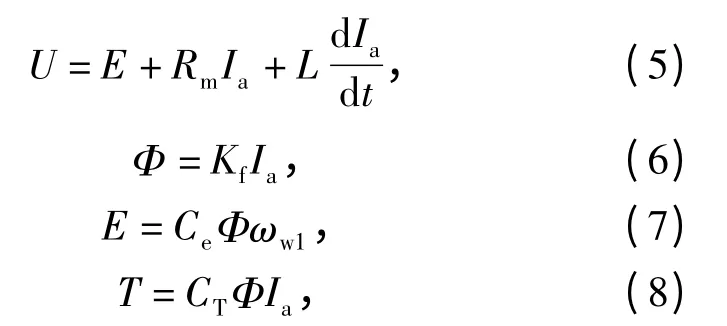
式中:U 为电机输入电压;E 为反电动势;Rm为电阻;Ia为电枢电流;L 为电感;Φ 为主磁通;Kf为励磁系数;Ce为反电动势系数;ωw1为电机转速;T 为电机输出转矩;CT为电磁转矩系数。

电机的控制与驱动方案如图4 所示，电机含有两个方向相反的励磁绕组，用来产生正向和反向驱动力矩，功率器件采用绝缘栅双极型晶体管(IGBT). 控制信号由比例-微分闭环控制产生，控制信号为正时，与正向励磁绕组相连的IGBT 导通，与反向励磁绕组相连的IGBT 断开;控制信号为负时，与正向励磁绕组相连的IGBT 断开，与反向励磁绕组相连的IGBT 导通。为防止两个励磁绕组同时接通，在触发电路中放置了门限电路，使得IGBT 的导通具有了迟滞性。协调定位时，励磁绕组上的电压为准脉冲形式，在功能上类似于脉宽调制。

图4 电机的控制与驱动框图Fig.4 Control and drive block diagram of motor

根据图4 在Simulink 中建立仿真模型中的控制模块。

2 不确定性变量与误差加权方法

2.1 不确定性变量及空间标准化转换

协调器工作时，可能受到由火炮射击带来的扰动;蜗杆蜗轮齿面之间受力大、受力情况复杂、不确定性明显，是协调过程中的关键受力面，蜗杆蜗轮间摩擦性能变化会对定位效果产生明显影响;小平衡机力直接加在支臂上，协调性能对小平衡机压力变化比较敏感，造成该力变化的主要原因是环境温度的不确定性;在自行火炮工作中，车载电源需要同时给多套设备供电，可能造成协调器驱动电机的电压不稳定。

故选择此4 个变量作为不确定性变量进行分析:扰动幅值系数R，蜗轮蜗杆间接触摩擦系数μ，多变指数na，电机输入电压U.

所掌握的以上4 个变量的不确定性情形如表1所示。

对不确定性变量空间进行坐标变换，使得区间下界映射到标准空间中对应坐标的-1 处，区间上界映射到+1 处，均值映射到0 处。由于不确定性变量的均值不一定为区间上界和下界二者的均值，需要选择单调的凹函数或者凸函数进行非线性变换。本文选择映射函数:

表1 不确定性变量Tab.1 Uncertain variables

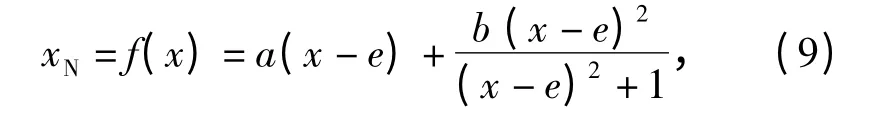
式中:xN为标准空间中的坐标;e 为变量均值;a、b为函数的系数，可根据各个变量的映射关系求出。

假设误差函数ε(X)较为连续且平滑时，考虑ε(XN)在标准空间内的分布与可靠性的关系，可知:

1)极限状态曲面ε(XN)=ε0的中心越靠近空间的原点(即均值点)可靠性越高;

2)极限状态曲面围成的区域(即安全域)越大可靠性越高。

例如图5 中3 种情形中，B 的可靠性高于A，C的可靠性高于B.

图5 3 个不同的极限状态曲面Fig.5 Three different limit state surfaces

所以即使不计算可靠性数值，在迭代过程中遵循以上两种趋势，也能实现提高可靠性的最优化设计。

2.2 误差权值与性能参数

在略大于不确定性变量区间范围内进行采样。假设采样是比较均匀的，为使得误差加权和对接近均值点的采样点的误差值更加敏感，同时考虑到以采样点到原点距离为尺度时，距离越大，采样密度越大，本文使用高斯函数作为误差权值函数:

式中:dk为标准空间中第k 个采样点到原点的距离;c 为均值点加权系数与顶点加权系数之比。均值点处d=0，cerror=1;而标准空间中不确定性变量分布区间围成的4 维超立方体顶点处d =2，cerror =1/c.

对每个采样点，将坐标值赋值到Simulink 中的参数中进行仿真，获得定位误差(绝对值形式)。将定位误差与相应的权值相乘取和作为性能参数:

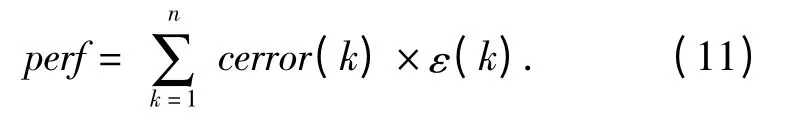
在安全域内有ε(XN)＜ε0，而且在误差函数ε(XN)不过分崎岖的情况下，大致上越接近极限状态曲面，ε 越大;越接近安全域的内部，ε 越小。

对于性能参数，由于越接近均值点具有越大的加权系数，故欲使性能参数perf 变小，要么降低整体的误差，使得安全域变大，要么使安全域的中心靠近均值点，即2.1 节所述的两种提高可靠性的趋势。

c 的取值与不确定性变量空间的维数及采样有关，并带有一定的主观性。本文采用拉丁超立方采样方法(LHS)，该采样方法具有更好的采样均布性和样本效率［7］，使用的采样点数为100，对每个采样点分别进行协调目标角度为25°和60°的动力学仿真并获取定位误差，故n =200，不确定性变量的维数为4，取c=20. cerror 与d 的关系如图6 所示。

图6 误差加权系数Fig.6 Error weights

3 粒子群优化

3.1 粒子群优化算法概述

粒子群优化算法(PSO)是一种模拟鸟群社会行为的群体搜索算法，粒子群中的粒子有一个基本的行为:仿效邻域个体的成功和他们自己的成功。从这个基本行为显现出来的集体行为就是在一个高维搜索空间中发现最优区域［8］。PSO 算法具有结构简单、参数较少、易于实现以及寻优能力强等优点［9］。

3.2 优化问题描述

取减速箱前两级传动比n1、n2，控制系统中角度反馈系数乘子Gθ，角速度反馈系数乘子Gω为优化的设计变量。

根据设计要求和对仿真模型的调试与分析，设定各设计变量的可取值范围，于是，本文的优化问题可描述为

3.3 优化流程

1)对不确定性变量进行拉丁超立方采样。

2)对不确定性变量进行坐标转换并计算采样点的误差加权系数cerror(k).

3)粒子群初始化，取种群大小16，初始化各粒子位置p(t，i，j)，其中t 为迭代次数，初始值t =1，i 为粒子标号，j 表示第j 维设计变量。运行Simulink进行协调过程仿真，获得定位误差ε(t，i，k)，计算性能参数初始化粒子最优位置y(t，i，j)和群最优位置(t，j)，初始化惯性权重w(t)=0.9，初始化粒子速度v(t，i，j)=0，加速系数c1=c2=1.

4)更新各粒子速度:

式中:r1(t，j)，r2(t，j)为0 ～1 间的随机值。

5)计算新的粒子位置:

6)分别检查每个粒子位置是否超出约束条件。如超出，更改v(t +1，i，j)=0，perf(t +1，i)=∞;否则运行Simulink 进行协调过程仿真，获得定位误差ε(t+1，i，k)，计算性能参数perf(t+1，i)=

7)根据性能参数更新粒子最佳位置y(t +1，i，j)和群最佳位置(t+1，j).

8)检查终止条件:群最佳性能参数取得收敛或达到最大迭代次数tmax. 若达到最大迭代次数而未收敛，回到步骤3 重新进行粒子群的随机初始化;若取得收敛，终止程序;否则，更新惯性权值:

9)重复步骤4 ～8，直到满足终止条件。

3.4 优化结果

进行3 次不同的不确定性变量采样，分别进行优化，取收敛后群最佳性能最小的一次作为优化结果。优化过程中群最佳性能的收敛过程如图7 所示。设计变量的最优解为:减速箱前两级传动比n1=3.27，n2=3.03;控制系统中角度反馈系数乘子Gθ=1.64;角速度反馈系数乘子Gω=1.00. 对齿轮传动比进行规整，最优设计变量取:n1=87/27 =3.22，n2=57/19 =3;Gθ=1.64，Gω=1.00.

图7 群最佳性能收敛过程Fig.7 Convergence process of swarm optimum performance

对比图8 与图9 中采样点定位误差与标准空间中采样点到原点的距离的分布关系可以看出，优化后(见图9)样本整体误差下降，且大致上误差越大离均值点越远。可由此推测，安全域更大且安全域的中心更加靠近均值点，即实现了2.1 节中的两个优化目标。

图8 优化前采样点ε(k)与dk 分布关系Fig.8 ε(k)and dk of samples before optimization

4 结论

图9 优化后采样点ε(k)与dk 分布关系Fig.9 ε(k)and dk of samples after optimization

本文利用Simulink 建立了火炮弹药协调器机电系统模型，并对定位过程中的不确定性因素进行了分析。对不确定性变量进行了空间变换和拉丁超立方采样，根据空间变换后采样点到均值点的距离计算误差权值后，对每个采样点进行Simulink 仿真，将获取的定位误差值进行加权取和，通过粒子群算法对此加权和进行了优化。优化后样本整体误差明显下降，并且由于误差权值的作用，使得大致上误差越大的点离均值越远。根据对可靠性与标准空间中安全域分布关系的分析，此方法间接提高了协调器的定位精度可靠性。

References)

［1］侯保林，樵军谋，刘琮敏. 火炮自动装填［M］. 北京:兵器工业出版社，2010.HOU Bao-lin，QIAO Jun-mou，LIU Cong-min. Ammunition automatic loading system of howitzer［M］.Beijing:Publishing House of Ordnance Industry，2010.(in Chinese)

［2］Nikolaidis E，Ghiocel D M，Singhal S.Engineering design reliability handbook［M］.Boca Raton:CRC Press，2005.

［3］潘林锋，周昌玉，陈士诚.基于Kriging 模型的非概率可靠度计算［J］.应用力学学报，2010，27(4):791 -794.PAN Lin-feng，ZHOU Chang-yu，CHEN Shi-cheng.Non-probability reliability calculation based on Kriging model［J］.Chinese Journal of Applied Mechanics，2010，27(4):791 -794. (in Chinese)

［4］吕震宙，杨子政.基于神经网络的可靠性分析新方法［J］. 机械强度，2006，28(5):699 -702.LYU Zhen-zhou，YANG Zi-zheng. New reliability analysis method based on artificial neural network［J］. Journal of Mechanical Strength，2006，28(5):699 -702. (in Chinese)

［5］Valdebenito M A，Schueller G I. A survey on approaches for reliability-based optimization［J］.Struct Multidisc Optim，2010，42:645 -663.

［6］汪国梁. 单相串激电动机［M］. 西安:陕西科学技术出版社，1980.WANG Guo-liang. Single phase universal motor［M］. Xi’an:Shaanxi Science and Technology Press，1980. (in Chinese)

［7］Roshanian J，Edrahimi M.Latin hypercube sampling applied to reliability-based multidisciplinary design optimization of a launch vehicle［J］. Aerospace Science and Technology，2013，28:297 -304.

［8］Engelbrecht A P. Computational intelligence:an introduction［M］. 2nd ed. New York:John Wiley ＆ Sons，INC，2009.

［9］王维博.粒子群优化算法研究及其应用［D］. 成都:西南交通大学，2012.WANG Wei-bo.Research on particle swarm optimization algorithm and its application［D］. Chengdu:Southwest Jiaotong University，2012. (in Chinese)