基于地磁与卫星组合的高旋弹丸滚转角高频测量及系统误差计算研究

曹鹏，于纪言，王晓鸣，姚文进，吴有龙

(南京理工大学 智能弹药技术国防重点学科实验室，江苏 南京210094)

0 引言

弹丸姿态角的测量是弹道修正弹的关键技术之一［1］。目前弹丸姿态角的测量方法有很多，其中包括卫星、陀螺、加速度计及磁探测等方法。然而单一的测量模式，都会因自身问题而限制系统的全姿态角测量及测量精度，例如:卫星更新频率低且不能测量弹丸滚转角;陀螺系统误差随时间而累积且不能抗高过载;加速度计无法适用于高动态环境;磁探测需要引入一个或两个外部已知角。卫星能提供速度倾角与偏角，并能提供位置信息补偿磁测量，而地磁信息能基于此完成滚转角的计算。因此，基于地磁与卫星组合的弹丸滚转角计算将可能成为一种有效姿态角测量方法。

目前关于地磁与卫星组合测量弹丸姿态角方案的研究中，杨小军等［2］与牛春峰等［3］采用卡尔曼滤波方法对弹丸的位置与姿态参数进行状态估计，但均采用了简化的弹道模型;史连艳等［4-5］对该方案的可行性及制导精度进行了简单分析，并在后续研究中利用拟牛顿法来进行姿态解算。以上研究均未全局考虑组合测量的系统误差。裴东兴等［6］基于单轴假设，利用地磁计算了弹丸的炮口角速率。针对无法通过实弹及半实物仿真实验的方法来验证地磁与卫星组合测量弹丸滚转角的可行性及精度问题，本文基于小攻角及单轴旋转假设，建立了地磁与卫星组合的弹丸滚转角及其角速率的计算方法，并推导了该假设下滚转角及其角速率的系统误差。通过建立以俯仰角为变量的系统误差仿真参数模型，完成全弹道域实时变化的弹丸滚转角及其角速率的系统误差计算，并通过4 个方向的独立6 自由度(DOF)外弹道仿真，验证了系统误差仿真计算的正确性及高频计算的可行性。

1 地磁与卫星组合的姿态测量原理

1.1 基于地磁的姿态测量原理

地磁测量单元捷联安装在弹体上，磁传感器的敏感轴方向与弹体坐标系方向一致。在弹丸飞行过程中，通过弹载地磁测量单元实时测量地磁数据，可以得到地磁与弹体姿态角的关系方程为

式中:hnx、hny、hnz为导航系(北东地坐标系)下的地磁分量;hbx、hby、hbz为地磁矢量在弹体坐标系的投影;ψ、θ、γ 分别为导航系到弹体系按z、y、x 轴顺序旋转而得的偏航角、俯仰角和滚转角。

由(1)式可知，对于单一地磁矢量组成的坐标转换方程，求解姿态角时存在无数解，无法得到唯一解。因此，仅仅依靠地磁测量模块实时测量弹体坐标系下的地磁信息，无法完成姿态角的解算。

1.2 地磁与卫星组合的弹丸滚转角测量原理

由外弹道知识可知，在弹丸飞行过程中，弹丸稳定飞行的上升阶段及下降阶段，满足弹丸攻角为小攻角(攻角为αt，αt≈(a2+ b2)0.5)的条件，而在大射角的初始阶段与弹道顶部阶段，可能出现大攻角［7］。在弹轴与速度坐标系下，满足如下关系式:

式中:a、b 分别为高低攻角和侧滑角;θV、ψV分别为弹道倾角和弹道偏角。

利用弹载卫星设备，可实时测量弹丸所在位置的经度、纬度、高度及速度信息。在速度与导航坐标系中，利用卫星提供的速度信息，即可得到弹道倾角与弹道偏角，其计算公式如下:

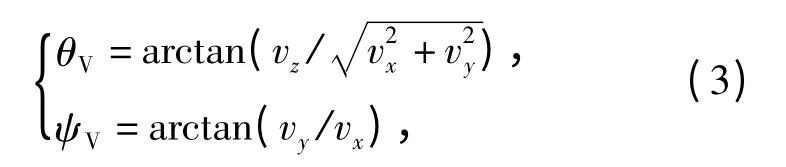
式中:vx为北向速度;vy为东向速度;vz为地向速度。

基于弹丸的小攻角假设可得，高低攻角和侧滑角a、b 为小量。因此，可以直接利用弹道倾角和偏角θV、ψV代替弹丸的俯仰角和偏航角θ、ψ. 即可认为弹道倾角和偏角为带有测量误差的俯仰角和偏航角。

已知俯仰角和偏航角，利用(1)式可得弹丸滚转角的计算公式

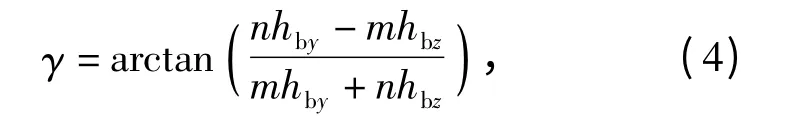
式中:m 与n 为中间变量，定义为

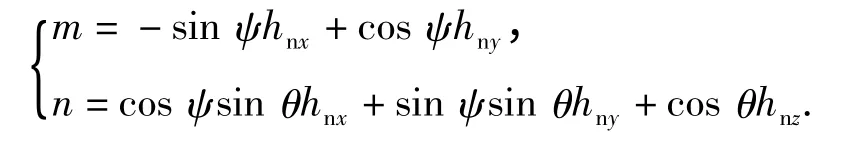
1.3 组合测量系统误差模型

由(4)式可得弹丸滚转角的另一种函数表达形式，如下式:

在利用(5)式计算弹丸的滚转角时，基于小攻角的假设，采用弹道倾角和偏角代替弹丸俯仰角和偏航角，即认为弹道倾角和偏角为带有测量误差的俯仰角和偏航角。令俯仰角与偏航角的角增量误差为δθ 与δψ，即

(5)式可以得到滚转角的误差方程为

从(7)式可以看出，基于小攻角假设的弹丸滚转角计算误差，与参考磁分量hnx、hny、hnz、俯仰角θ和偏航角ψ 及其增量误差δθ、δψ 相关。

在这一节中，基于弹丸的小攻角假设，完成了地磁与卫星组合计算弹丸滚转角的数学推导，并推导出该假设下的系统误差解析式。

2 组合测量系统的高频测量

2.1 高旋弹丸的高频测量原理

对于高速旋转弹丸，在弹丸飞行的全弹道过程中，弹丸的滚转角速率远远大于俯仰角及偏航角速率即在一个短的时间内，可以假设弹丸仅仅只有滚转角的变化，由(1)式整理可得

式中:A 与α 为中间变量，定义为

由(8)式可令滚转平面地磁输出为

式中:A 为磁测量幅值;f 为磁测量变化频率;t 为磁测量时间序列;φ 为初始偏移角。

基于单轴旋转假设，由(8)式和(9)式可得其滚转角速率为

2.2 高频测量误差模型

由(8)式和(9)式可得，滚转平面的地磁输出函数为幅值与周期变化的三角函数，其频率为

由(11)式可知，基于单轴旋转假设的滚转角速率计算误差即为. 令俯仰角与偏航角的角速率分别为与，由(8)式中α 的关系式可得

式中:

由(12)式和(13)式可以看出，基于单轴旋转假设的弹丸滚转角速率计算误差的影响因素包含:参考磁分量hnx、hny、hnz，俯仰角θ 和偏航角ψ 及其角速率

在这一节中，基于高速旋转弹丸的单轴旋转假设，完成了弹丸滚转平面磁测量频率变化计算滚转角速率的数学推导，并推导出了该假设下的系统误差解析式。

3 组合测量的系统误差研究

3.1 系统误差变量的取值

由6DOF 外弹道理论可知，俯仰角和偏航角增量δθ、δψ 及其角速率误差的值并非固定，而是随外弹道飞行阶段变化而变化，即:弹丸飞行稳定上升阶段至弹道顶点，攻角逐渐增大;由弹道顶点至弹丸下降阶段，攻角又逐渐减小。弹丸的飞行阶段不仅可以用时间描述，还可用俯仰角描述。因此，在研究小攻角及单旋转假设的系统误差时，可利用6DOF仿真数据，建立以俯仰角为变量的误差变量δθ、δψ及的仿真参数值。

以南京某地E118.85°、N32.03°地磁场为例，俯仰角及偏航角分别以步长Δ 变化，建立其系统误差的仿真参数。其仿真条件如表1 所示，得到误差变量δθ、δψ 及的值如图1 和图2 所示。

表1 系统误差仿真参数Tab.1 Simulation parameters of systematic errors

由外弹道知识可知，射角越大其最大攻角也就越大。从图1 可看出，在55°射角下，俯仰角与偏航角误差值的取值范围分别为:- 1° ＜δθ ＜1°与-1° ＜δψ ＜5°. 从图2 可看出，高速旋转弹丸的俯仰角及偏航角角速率取值范围为:-2.5°/s ＜＜0°/s 与-1.0°/s ＜＜0.5°/s，远远小于滚转角速率(初始角速率约为86 000°/s，落地角速率约为48 000°/s)。

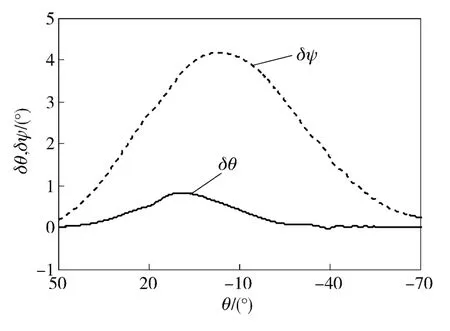
图1 俯仰角和偏航角误差参数Fig.1 Errors of pitch and yaw angles

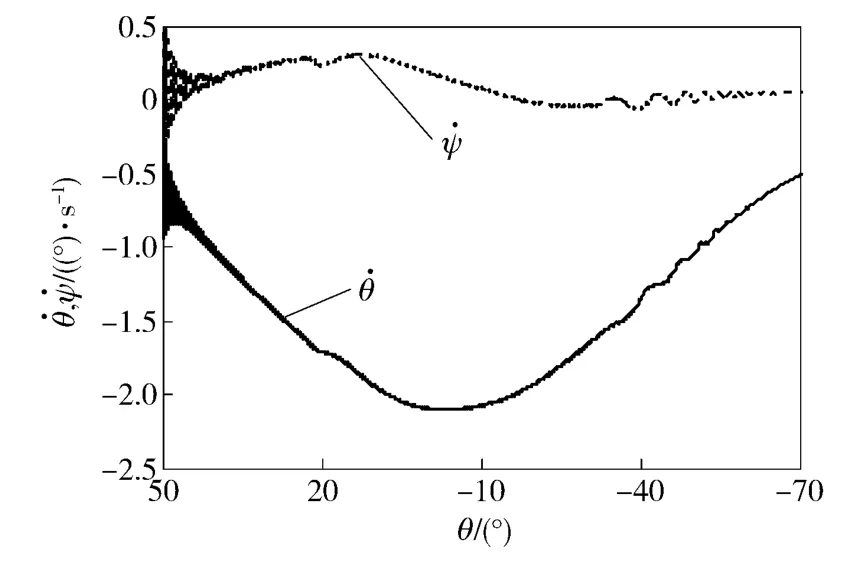
图2 俯仰角和偏航角角速率参数Fig.2 Pitch and yaw angular velocities

3.2 组合测量系统的误差计算

利用3.1 节的系统误差变量值，建立以俯仰角为变量的误差变量δθ、δψ 及的仿真参数值，再利用(7)式与(12)式即可完成全射向角区域(偏航角及偏航角取值见表1)的系统误差计算，如图3和图4 所示。

图3 为小攻角假设条件下，组合测量系统在全域范围内的滚转角误差等值线图。从图3 可看出，在小攻角假设条件下，地磁与卫星组合的弹丸滚转角计算误差范围为:绝大部分区域满足＜±5°. 图4为单轴旋转假设条件下，组合测量系统在全域范围内的滚转角速率误差等值线图。从图4 可看出，在单轴旋转假设条件下，弹丸滚转角速率计算误差范围为:绝大部分区域满足＜±5°/s.

图3 小攻角假设下的滚转角系统误差Fig.3 Systematic errors of roll angle under the assumption of small angle of attack

图4 单轴旋转假设下的滚转角速率系统误差Fig.4 Systematic errors of projectile roll angle rate under the assumption of single axial rotation

图3与图4 中均有两个相同的区域出现较大的误差，该区域中心位置为:ψ≈-5°≈D，θ≈-48°≈-I 与ψ≈175°≈D +π，θ≈48°≈I(D 为磁偏角，I为磁倾角)。当ψ=D，θ= -I 或ψ=D+π，θ=I 时，即弹轴与地磁矢量在同一直线上时，无法利用地磁信息计算任何角度。而当弹轴与地磁矢量有较小的夹角时，即使较小的俯仰角和偏航角误差及较小的俯仰角和偏航角角速率，也会带来较大的滚转角及其角速率误差。因此，在弹轴与地磁矢量有较小的夹角时，小攻角假设与单轴旋转假设下的滚转角及其角速率计算误差较大。排除该区域后，其整体滚转角误差小于±5°，角速率误差小于±5°/s.

4 弹道仿真验证

为了检验在小攻角和单轴旋转假设下组合的滚转角计算误差，以某型高旋弹丸为例，进行6DOF 外弹道仿真研究。外弹道仿真分别以正东(ψ =90°)、正南(ψ=180°或-180°)、正西(ψ = -90°)及正北(ψ=0°)4 个射向角发射，射角均为55°;地磁与卫星组合计算滚转角的频率为10 Hz(假定卫星速率数据更新频率为10 Hz);滚转平面的地磁旋转速率输出频率为200 Hz(模拟地磁采集频率最高可以达到5 MHz，即可满足200 Hz 的计算)，计算方法为取该周期内的频率f 的均值。最终滚转角计算误差仿真结果如图5 所示。

图5 组合滚转角计算误差Fig.5 Calculated error of combined roll angle

图5为在小攻角及单轴旋转假设条件下，组合测量系统频率为200 Hz 时，组合计算的弹丸滚转角与6DOF 外弹道仿真的差值。比较图5 与图3 可知，单次6DOF 仿真的滚转角误差在全域仿真的滚转角误差范围内。图5 中正南与正北方向相比正东与正西方向的滚转角误差大，对比图3 可知:正东与正西角度轨迹需穿越弹轴与地磁矢量较小的夹角区域。图5 中，正南方向θ =50°附近与正北方向θ =-40°附近的组合滚转角计算误差的波动较大，对比图4 可知:该区域用于高频计算滚转角的角速率误差较大。

由上面分析可知，6DOF 外弹道仿真结果验证了基于小攻角假设的组合测量方法以及基于单轴旋转假设的高频计算方法的可行性，同时也验证了建立以俯仰角为变量的系统误差计算模型的正确性。

5 结论

利用高速旋转弹丸的外弹道飞行特性，即在中小射角下，满足小攻角与单轴旋转假设的特性，建立了地磁与卫星组合的弹丸滚转角及其角速率计算方法。根据其计算原理，分别推导了地磁与卫星组合的弹丸滚转角及其角速度的系统误差方程。通过6DOF 外弹道仿真验证，可以得出如下结论:

1)在中小射角下，排除弹轴与地磁矢量小夹角的区域时，地磁与卫星组合测量的弹丸滚转角系统误差小于±5°，弹丸滚转角速率的系统误差小于±5°/s.

2)利用单轴旋转假设，建立了通过测量弹丸滚转平面的地磁旋转速率计算弹丸滚转角的方法，并以此获得了地磁与卫星组合的高频测量方法。该计算方法具有误差不随时间累积的优点，满足弹丸滚转角测量高频高精度的要求。

3)本文推导的地磁与卫星组合测量弹丸滚转角系统误差的解析式，及建立的以俯仰角为变量的系统误差参数的仿真计算方法，能较为准确地计算全射向角范围的系统误差。

References)

［1］岳明凯，曲家惠. 弹道修正弹药的关键技术和发展趋势［J］.飞航导弹，2009，9:25 -28.YUE Ming-kai，QU Jia-hui. The key technologies and trends of trajectory correction ammunition［J］. Aerodynamic Missile Journal，2009，9:25 -28.(in Chinese)

［2］杨小军，施坤林，汪仪林. 基于磁传感器/GPS 组合制导飞行弹体的姿态和位置估计［J］. 兵工学报，2008，29(2):169 -173.YANG Xiao-jun，SHI Kun-lin，WANG Yi-lin. Estimate of attitude and position of flying projectile controlled by combined guidance based on magnetometer/GPS［J］. Acta Armamentarii，2008，29(2):169 -173. (in Chinese)

［3］牛春峰，刘世平，王中原. 高速旋转弹位置与姿态测量数据分析方法［J］. 火力与指挥控制，2012，37(5):89 -92.NIU Chun-feng，LIU Shi-ping，WANG Zhong-yuan. Estimate of position and attitude of high-speed rotating projectile［J］. Fire Control ＆ Command Control，2012，37(5):89 -92. (in Chinese)

［4］史连艳，杨树兴，张夏庆. MR/GPS 制导在旋转火箭弹中的应用分析［J］. 弹箭与制导学报，2006，26(2):1145 -1147.SHI Lian-yan，YANG Shu-xing，ZHANG Xia-qing. Analyzing of MR/GPS guiding applied in rotating rocket-powered missile［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2006，26(2):1145 -1147. (in Chinese)

［5］史连艳，张自宾，宋文渊. 基于MR/GPS 的弹体姿态解算方法研究［J］. 系统仿真学报，2010，22(12):2948 -2951.SHI Lian-yan，ZHANG Zi-bin，SONG Wen-yuan. Study of rocket body attitude solving method based on MR/GPS［J］. Journal of System Simulation，2010，22(12):2948 -2951. (in Chinese)

［6］裴东兴，王文武，崔春生. 利用转速测试弹丸炮口速度的方法研究［J］. 兵工学报，2013，34(1):125 -128.PEI Dong-xing，WANG Wen-wu，CUI Chun-sheng. Study on projectile muzzle velocity measurement based on rotational speed［J］.Acta Armamentarii，2013，34(1):125 -128. (in Chinese)

［7］Robert L M. Modern exterior ballistics［M］. Atglen:Schiffer Publishing，1999.