PM2.5的时间分布与演变扩散研究

卢鹏, 何杰

(1.西南交通大学峨眉校区基础课部, 四川峨眉 614202; 2. 西南交通大学土木工程学院, 成都 610031)

PM2.5的时间分布与演变扩散研究

卢鹏1, 何杰2

(1.西南交通大学峨眉校区基础课部, 四川峨眉 614202; 2. 西南交通大学土木工程学院, 成都 610031)

最初利用时间序列——指数平滑法来分析PM2.5的时间分布情况. 考虑到在分析过程中不确定PM2.5与时间之间存在怎样的关系, 所以分别建立了一次、二次及三次指数平滑模型, 通过对比分析最终确定PM2.5与时间的具体关系. 为了更好的控制和治理PM2.5污染物, 则需要对其扩散规律进行分析, 基于此, 本文建立了基于高斯扩散模型的PM2.5污染物扩散模型, 建模过程中, 首先建立了大气稳定状态下的基本模型, 然后在此基础上又进一步建立了能够反映风速、温度以及湿度对PM2.5扩散产生影响的基本模型, 具有一定的适用性.

PM2.5; 时间分布; 指数平滑法; 高斯扩散

1 引言

随着社会的不断发展, 各城市的大气污染程度也在不断的加剧, 现如今大气污染状况已经成为了公众关注的焦点之一. 考虑到大气的污染状况不仅对环境有巨大的影响, 同时还关系着广大人民群众的健康和生命安全,所以需要对有关大气污染的问题进行深入的研究. 研究出合理的方案用于解决环境大气污染问题, 研究方案之前首先需要分析大气污染物的时间分布情况, 即大气污染物的含量随时间的变化呈现怎样的变化趋势, 之后则应该对大气污染的演变扩散规律进行相应的分析. 本文分析的对象是大气污染物中的细颗粒物(PM2.5), 研究的内容包括PM2.5含量随着时间呈现怎样的变化趋势, 以及PM2.5在大气中的扩散演变规律. 在此基础上进一步分析温度、湿度、风速等对PM2.5扩散演变的影响情况.

2 分析方法理论研究

2.1 时间分布分析法

考虑到PM2.5含量与时间存在很大的关系[1], 所以本文采用指数平滑法来分析PM2.5与时间的关系, 即PM2.5的时间分布情况. 为了深入的研究PM2.5浓度随着时间的变化趋势及分布情况, 首先建立了PM2.5浓度随时间变化的一次指数平滑预测模型[2]. 为了进一步验证结果的准确性,建立了二次、三次指数平滑预测模型, 通过对比分析三种模型的结果来确定PM2.5的时间分布情况, 以下以一次指数平滑预测模型为例建立模型.

也就是以第t期指数平滑值作为t+1期预测值.

2.2 高斯扩散模型

为了更好的分析PM2.5浓度在风力、湿度等天气和季节因素下的扩散情况, 首先建立了大气稳定状态下的基本模型[4], 然后在逐渐考虑其它因素的影响, 并建立了考虑大气温、湿度变化的PM2.5扩散模型.

2.2.1 大气稳定状态下的基本模型

由分子扩散的Fick定律[5](即梯度输送理论: 分子扩散的质量通量与扩散物质的浓度梯度成正比)和湍流扩散等扩散理论, 可以得到污染物迁移、转化的基本方程:

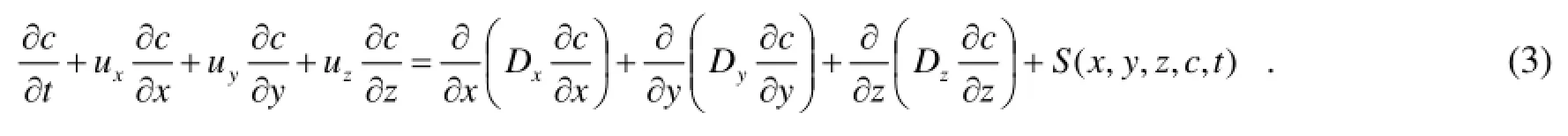
式中:

c: PM2.5在环境介质中的浓度, 单位mg/m3;

Dx,Dy,Dz: 为x,y,z 方向上的分子扩散系数;

Dmx，Dmy， Dmz: 表示湍流扩散系数, 单位m3/s ;

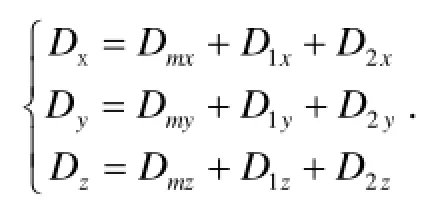
S（x ,y,z,c,t ）为考虑到环境介质中会由于物理、化学、生物等作用引起污染物的增减在公式中附加的一个源-汇项[6].

2.2.2 考虑大气温度、湿度变化的PM2.5扩散模型

在实际的大气环境中空气湿度对污染物在大气中的扩散影响较大, 对颗粒污染物(PM2.5等)的影响尤为明显. 当寒冷季节在水网地带气温较低, 湿度较大时, 水蒸气容易以烟尘、微尘为凝结核而形成雾, 使污染物粒子变重而下沉, 并积聚在低层空气中, 同时阻碍烟气的扩散, 加重了空气的污染. 所以有雾时, 空气中的污染物的浓度往往显著增高, 所以温湿度对PM2.5扩散影响需要进行考虑[7].

首先考虑湿度、温度等天气和季节因素的影响后, 对公式(2.3)进行改进. 改进过程如下:

由于空气温湿度主要影响分子扩散系数, 所以公式(2.3)可修正为:

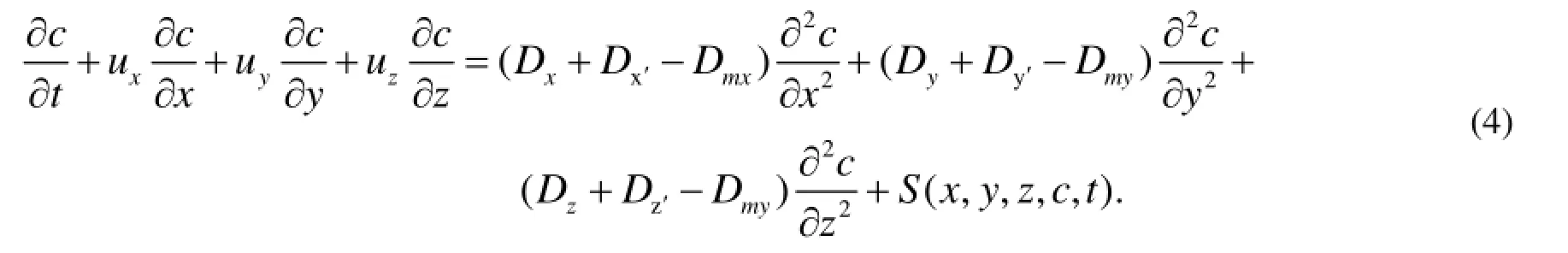
式中:

Dmx,Dmy,Dmz: 分别为在x,y,z 方向上在干空气中的分子扩散系数;

Dx′,Dy′,Dz′: 分别为在x,y,z 方向上湿空气中的分子扩散系数;

Dx′-Dmx, Dy′-Dmy,Dz′-Dmz: 分别为湿度对于分子扩散系数的影响变化量.

Dmx,Dmy,Dmz和Dx′,Dy′,Dz′的取值问题详见文献[8].

3 基于时间序列的时间分布结果

利用在西安市采集的PM2.5浓度值进行分析, 得到了在一次、二次、三次指数平滑的预测效果图, 如下所示:

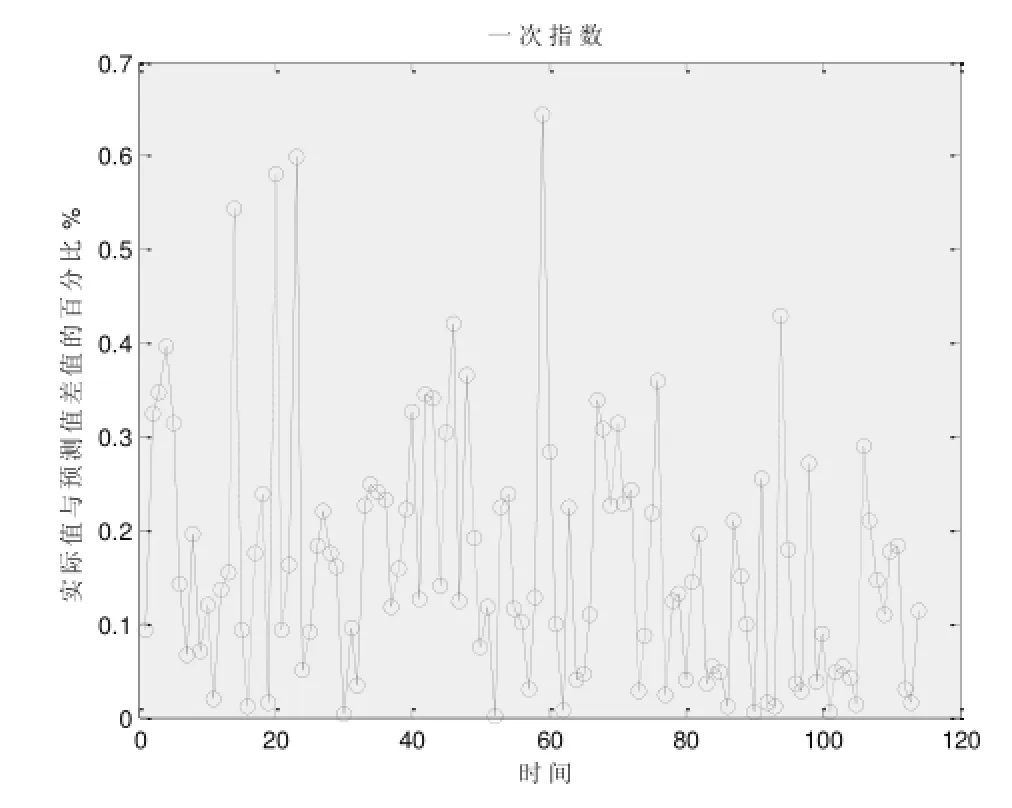
图1 一次指数平滑相对误差分析图

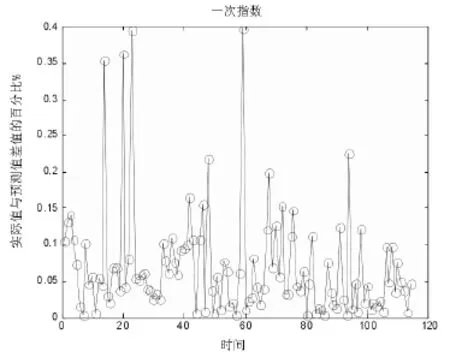
图2 一次指数平滑相对误差分析图

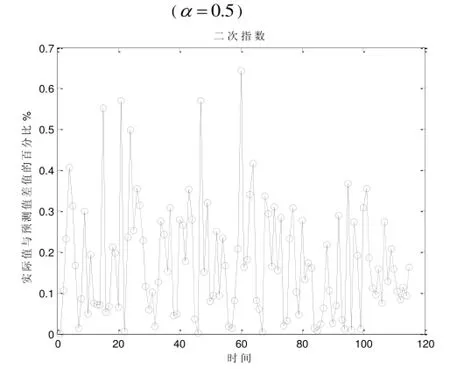
图3 二次指数平滑相对误差分析图

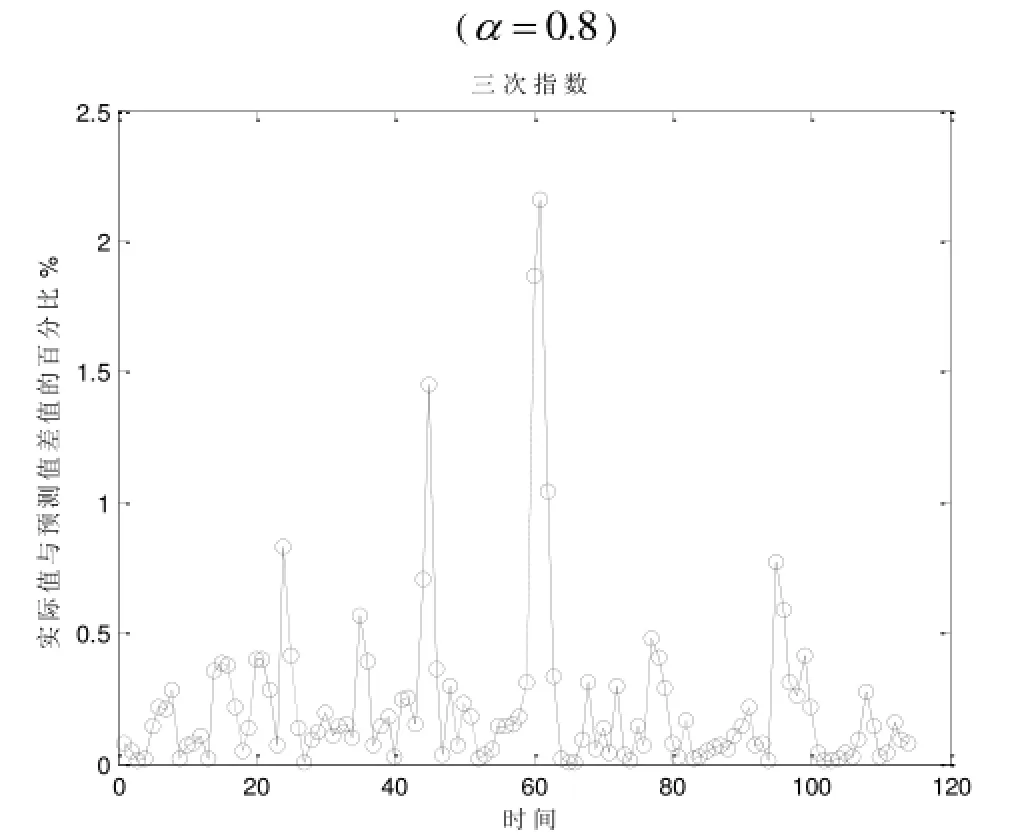
图4 三次指数平滑相对误差分析图

根据上述图形可知, 各阶次指数平滑预测值与实际值相对误差不超过2.5%, 且误差百分比集中在0%～0.5%范围内, 一次平滑指数预测精度最高, 这间接说明该地区PM2.5平均浓度与时间分布很紧密, 并且具有很强的分布规律, 可以通过指数平滑模型来进行PM2.5浓度的预测.

下图给出了西安市四个地区从2013年1月1日到2013年4月28日每15天PM2.5浓度平均值的柱状统计表, 如下所示.

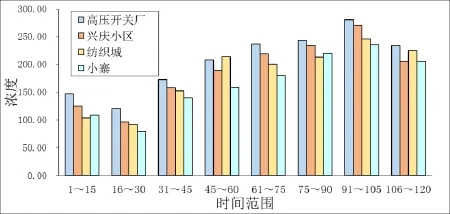
图5 各测点PM2.5浓度随时间统计图

由图5可知, 各监测点随着时间的变化规律基本一致, 1月到4月各测点PM2.5呈现逐渐递增的趋势, 这说明PM2.5与季节有一定的关系, 间接说明该地区PM2.5浓度与时间存在一定的联系.

4 基于高斯扩散模型的实验结果

利用在西安市采集的PM2.5浓度值进行分析, 得到了风速、温度以及湿度对PM2.5扩散的影响:

4.1 风速对PM2.5扩散的影响

为了研究风速对PM2.5扩散与衰减规律[9]的影响, 按照表1所示的计算参数, 分别求解了风速在5m/s (3级风)、10m/s (5级风)、20m/s (8级风)、30m/s (11级风)作用下的PM2.5扩散分布图, 研究风速对PM2.5污染物的影响, 计算结果如下图表所示

表1 研究风速影响的计算参数表

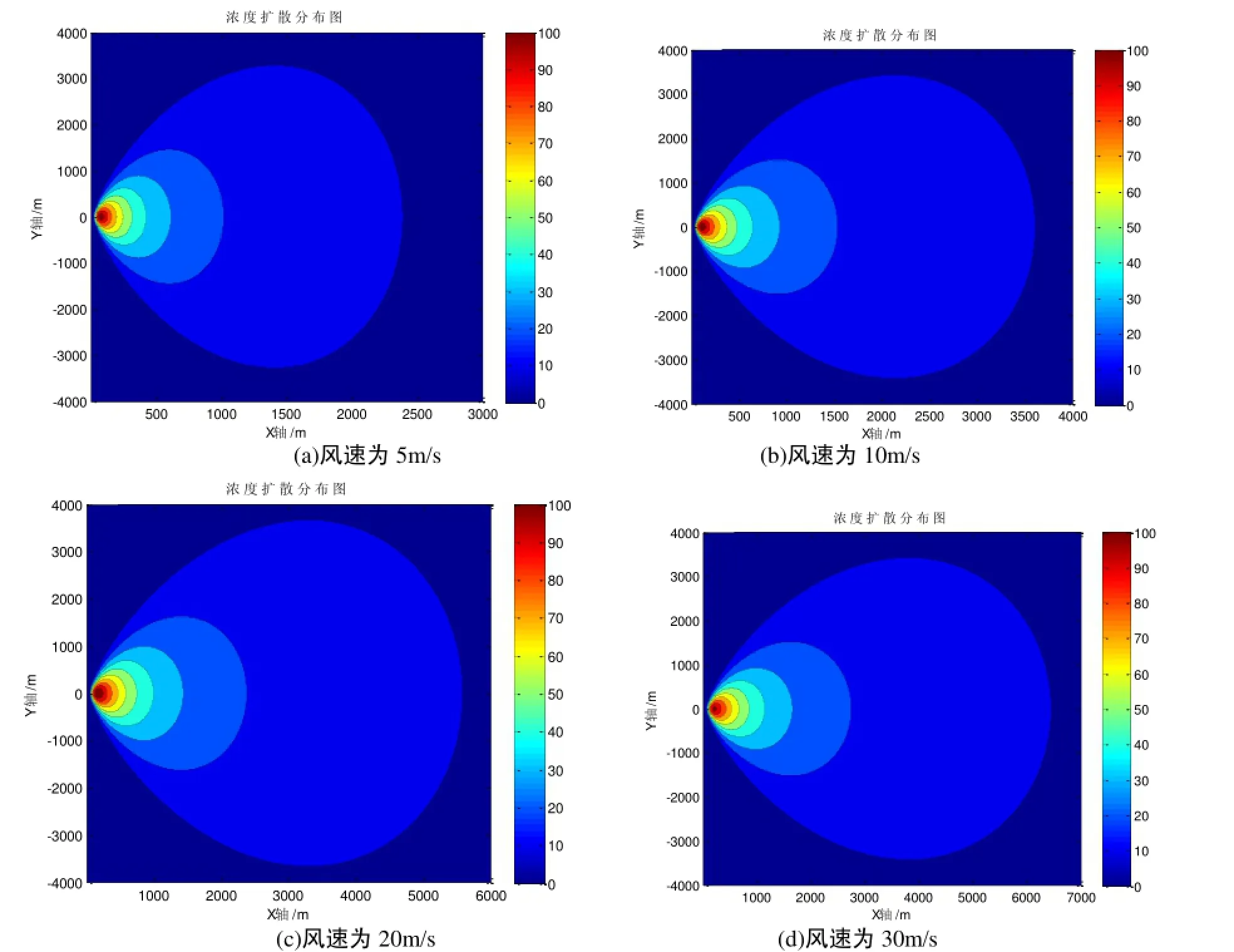
图6 不同温度作用下PM2.5扩散衰减分布图

由图可知, 随着风速的逐渐增加, PM2.5扩散范围在逐渐增大, 影响面积也在不断的扩大, 沿着风速方向的影响距离在不断增加, 因此风速对PM2.5污染物的影响较明显.

4.2 湿度PM2.5扩散的影响

为了研究湿度对PM2.5扩散与衰减规律[10]的影响, 在其他参数保持不变的情况下, 分别求解了湿度在20%、40%、60%、80%的PM2.5污染物扩散结果. 结果如下图所示:

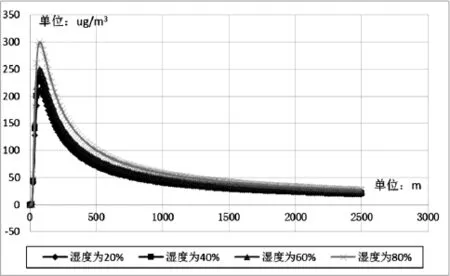
图7 不同湿度条件下PM2.5污染物地面浓度纵向中心分布图

由上图可知, 随着湿度的增大, PM2.5的扩散分布变化不大, 随着湿度的增加扩散也在逐渐增加, 但影响较小.

4.3 温度对PM2.5扩散的影响

为了研究温度对PM2.5扩散与衰减规律的影响, 在其他参数保持不变的情况下, 分别求解了温度在10、20、30、40摄氏度的PM2.5污染物扩散结果. 结果如下

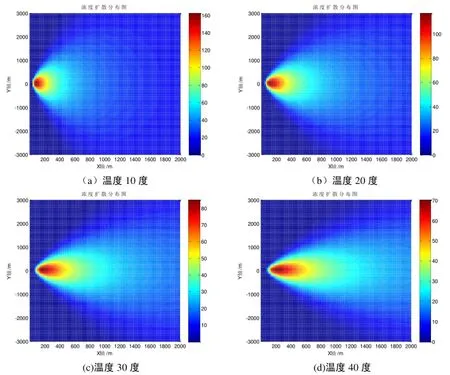
图8 不同温度下PM2.5的扩散分布图

由图可知, 随着温度的逐渐增加, PM2.5扩散范围在逐渐增大, 影响面积也在不断的扩大, 因此温度对PM2.5污染物的影响较明显.

5 结语

通过利用时间序列分析可知PM2.5平均浓度与时间分布很紧密, 且具有很强的分布规律, 即可以利用指数平滑模型来进行PM2.5浓度的预测. 为了更好的控制治理PM2.5的污染情况, 本文建立了PM2.5的扩散模型,并得到了如下一些结论, 首先随着风速以及温度的逐渐增加, PM2.5扩散范围会逐渐增大, 影响面积也会不断的扩大, 且沿着风速方向的影响距离会不断增加; 其次随着湿度的增大, PM2.5的扩散分布变化不大, 随着湿度的增加扩散也在逐渐增加, 但影响较小. 可见, 风速、温度以及湿度会在一定程度上影响PM2.5污染物的扩散情况.

[1] 司守奎, 孙玺清. 数学建模算法与应用[M]. 北京: 国防工业出版社, 2012.

[2] 韩忠庚. 数学建模方法及其应用[M]. 2版. 北京: 高等教育出版社, 2009.

[3] 姜启源, 谢金星, 叶俊. 数学模型[M]. 3版. 北京: 高等教育出版社, 2003.

[4] 郭遵强. 大气污染扩散模型的研究及在环境应急系统中的实现[D]. 青岛: 中国海洋大学, 2008.

[5] 伊凤. 大气污染物扩散的理论和试验研究[D]. 青岛: 中国海洋大学, 2006.

[6] 彭希珑. 南昌市大气PM10与PM2.5的污染特征及来源解析[D]. 南昌: 南昌大学, 2009.

[7] 杨天智.长沙市大气颗粒物PM2.5化学组分特征及来源解析[D]. 长沙: 中南大学, 2010.

[8] M S AHUJA, J PASKIND, J E HOUCK, et al. Design of a Study for the Chemical and Size Characterization of Particulate Matter Emissions from Selected Sources in California[R]. In Transactions: Receptor Models in Air Resources Management, 1989.

[9] US EPA. National ambient air quality standards for particulate matter (Final Rule)[S]. Federal Register, 1997, 62: 3865138760.

[10] 吴国平, 胡伟, 滕恩江, 等. 我国四城市空气中PM2.5和PM10的污染水平[J]. 环境学研究, 1999, 19(2): 133-137.

The research of PM2.5's time distribution and evolution of diffusion

LU Peng1,HE Jie2
(1. Emei Campus, Southwest Jiaotong University, Emei 614202, P.R.C.;
2. College of Civil Engineering, Southwest Jiaotong University, Chengdu, P.R.C.)

This article uses time series analysis---the exponential smoothing method to analyze the time distribution of PM2.5. Considering the uncertainty relationship between PM2.5 and time in the process of analysis, primary, secondary and three exponential smoothing models are established respectively. Through the comparison and analysis, the relationship between PM2.5 and time is determined eventually. For the purpose of better control and governance of PM2.5 pollution, it is necessary to analyze its dispersion characteristics. Based on this, this paper establishes the PM2.5 pollutant diffusion model foundation of Gaussian diffusion model. During the process of modeling, the basic model of atmospheric stability condition is established, and further, a model is established that can reflect wind speed, temperature and humidity on the basic model of PM2.5 diffusion effects, which has a certain applicability.

time distribution; exponential smoothing; Gaussian dispersion

O212

A

1003-4271(2014)01-0066-06

10.3969/j.issn.1003-4271.2014.01.14

2013-11-10

卢鹏(1983-), 男, 讲师, 研究方向为数学建模理论与方法, 粗糙集理论与应用; 何杰(1990-), 男,硕士研究生, 研究方向为桥梁结构健康监测与损伤识别.