基于虚拟样机技术的齿轮摩擦动力学仿真

李宝良，陶雪娟

(大连交通大学 机械工程学院，辽宁 大连 116028)*

0 引言

随着现代科学技术的不断发展与进步，人们对齿轮的应用越来越广泛，进而对其力学性能的要求也有所提高.在齿轮传动的过程中，齿间摩擦力引发齿面磨损，从而导致齿轮失效.因此在齿轮动力学方面的研究过程中，研究人员研究了齿间摩擦力对齿轮动力学的影响.

目前研究人员黄泽平等人［1］对齿轮系统进行了动力学仿真，得到了单对轮齿间的法向力及摩擦力的变化规律曲线，但该研究只分析了某一特定传动条件下的单对轮齿，并没有对其它轮齿进行全面分析.谢永智［2］探讨了齿轮偏心等缺陷对啮合力的影响，同时刘涛等人［3］研究了锥齿轮动态啮合过程中输入、输出轴转速及啮合力的变化规律，而方子帆等人［4］计算了在输入转速和载荷的共同作用下各级齿轮的动态啮合力，但均未分析齿轮转速对该啮合力的影响.周旭辉等人［5］通过动力学仿真分析了摩擦系数和渗透深度等参数随时间变化的规律，但研究结果仅适用于齿轮与齿条间的啮合情况.

基于以上研究可以看出，虽然在齿轮动力学方面已经取得了一定的成绩，但是研究人员从摩擦角度出发，对齿轮动力学的研究仍然需要进一步的完善和研究.因此以渐开线直齿圆柱齿轮为研究对象，对其进行动力学仿真，获得齿轮上某一点从啮入到啮出完整周期内的压力、摩擦力的载荷谱，并研究啮合过程中齿轮摩擦力的变化趋势，分析主动齿轮转速对齿轮正压力、摩擦力的影响，从而为齿轮系统优化设计提供理论参考.

1 齿轮虚拟样机模型的建立

1.1 虚拟样机模型的建立

以某通用单级减速器中的渐开线直齿圆柱齿轮为研究模型，通过查阅相关文献资料［6-7］计算得到齿轮的几何参数如表1所示，利用Geartrax插件的方法，建立齿轮模型，并在Solidworks中完成装配以及干涉检查等操作.

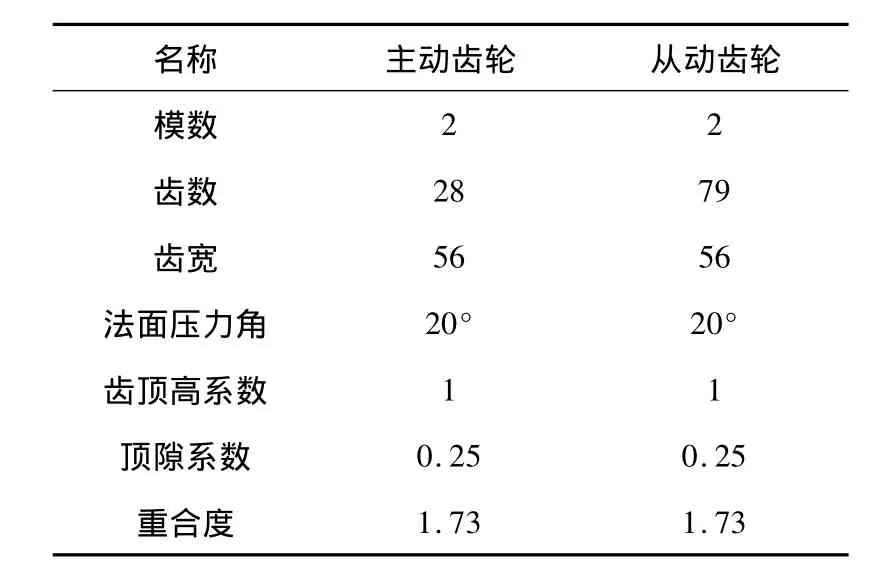
表1 齿轮几何参数

完成齿轮的几何建模后，应用文件专用传输接口的Parasolid格式将SolidWorks中的模型数据导入到ADAMS中，定义模型的物理属性，添加接触［8］、旋转副，施加负载扭矩.

1.2 齿轮摩擦系数的定义

选取的摩擦系数与齿轮所处的啮合接触位置有关.根据前期研究所获得的摩擦系数公式可计算出各个啮合位置的摩擦系数，具体计算表达［9］:

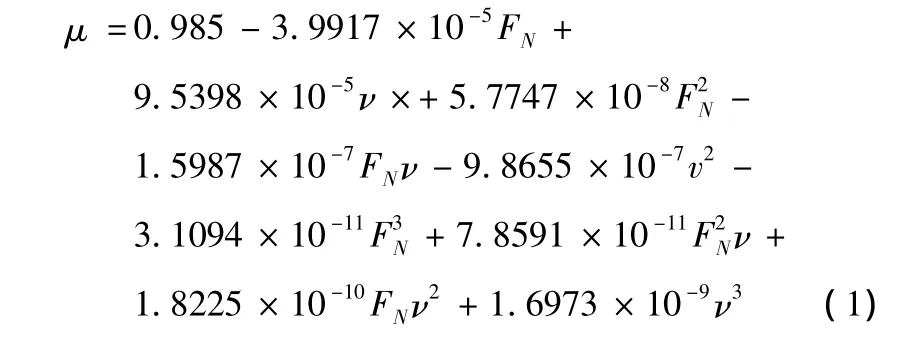
式中:μ为啮合处的摩擦系数;ν为啮合处的相对滑动速度;FN为法向载荷.

由式(1)可求得在主动齿轮转速不同的情况下，齿轮处于不同啮合位置时的摩擦系数，其中f1、f2、f3分别代表转速为 675、750、960 r/min的摩擦系数，如下表2所示.

表2 不同啮合位置时的摩擦系数

经过以上步骤，已经完成对渐开线直齿圆柱齿轮摩擦动力学仿真模型的创建以及相关参数的设置.齿轮啮合虚拟样机模型如图1所示.

图1 齿轮啮合虚拟样机模型

2 仿真结果分析

2.1 后处理的设置

在仿真分析开始之前，需对该仿真模型进行检验，排查建模过程中是否存在不恰当的连接或约束，质量定义不完全等情况，从而确保能够顺利地进行仿真分析.在确定仿真模型的创建是正确的前提下，便可以对该模型进行仿真设置，分别设置仿真时间为0.1 s，步数为2 000，仿真类型为Default.

2.2 仿真结果的验证

为了检验渐开线直齿圆柱齿轮的摩擦动力学仿真模型是否可靠，需通过对该仿真模型进行动力学仿真并将仿真所得到的结果与其理论数值进行对比分析.经过动力学仿真之后，得到了主动齿轮角速度为4 050、4 500、5 760(°)/s的从动齿轮角速度和齿轮间啮合力并分别表示为ω1、ω2、ω3、Fn1、Fn2、Fn3.现根据机械设计中的相关计算公式计算齿轮间啮合力与从动齿轮角速度的理论数值以及各自的误差值，如表3所示.

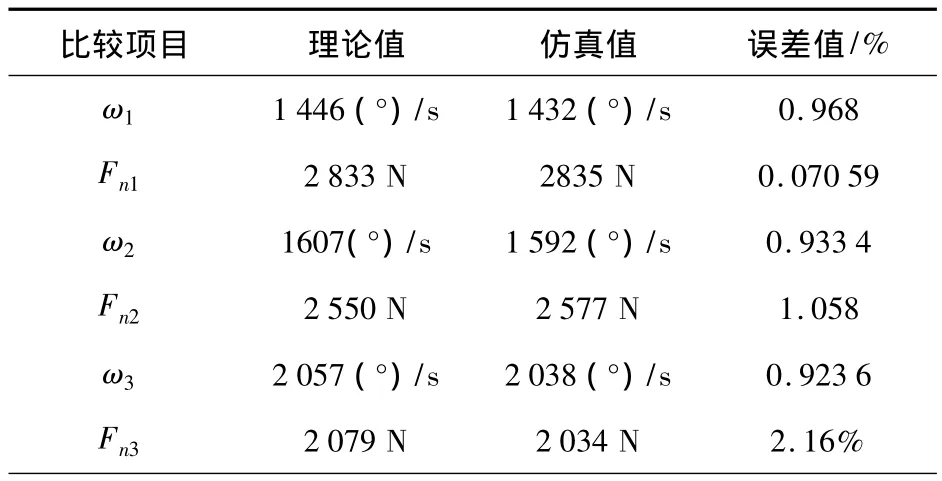
表3 理论计算值和仿真分析值的比较

由表3得知:齿轮间啮合力与从动齿轮转速误差值均未超过5%，可以认为该参数的理论数值与仿真数值二者基本吻合，表明齿轮的摩擦动力学仿真模型具有可靠性，并且考虑摩擦影响的齿轮间啮合力与从动齿轮转速才能更为真实的反映实际状态，分析更为准确.

2.3 不同啮合位置齿轮摩擦力的分析

由于在齿轮啮合过程中，参与啮合的两轮齿的摩擦系数是不断变化的.所以将摩擦系数取为定值，并不符合齿轮传动的真实情况.需以稳定啮合阶段中的某对轮齿作为研究对象，依据各个啮合位置的齿轮摩擦系数，对齿轮的接触进行定义，从而得到齿轮从进入啮合到退出啮合的过程中，该齿轮转过角度为 5°、10°、15°、25°时的正压力、摩擦力(表4)，同时作出正压力、摩擦力随齿轮转角变化的曲线图.其中θ为齿轮转过角度;FN1、FN2、FN3、f1、f2、f3分别为主动轮转速是 675、750、960 r/min时的齿轮正压力、摩擦力.

表4 不同啮合位置的正压力、摩擦力

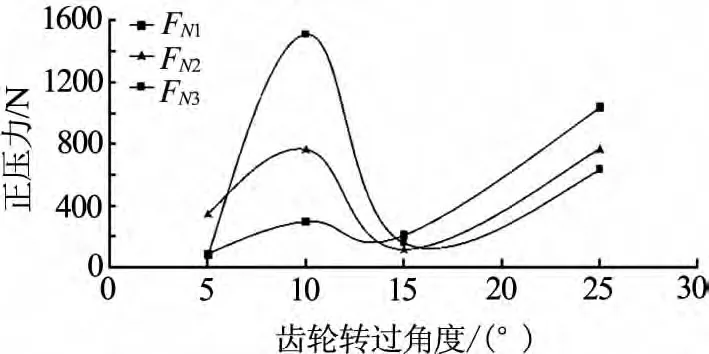
图2 不同转速下齿间正压力与齿轮转过角度的关系

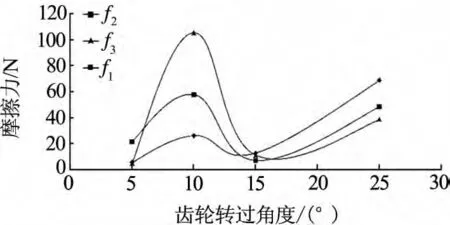
图3 不同转速下齿间摩擦力与齿轮转过角度的关系

由图2图3可知:虽然主动齿轮转速有所不同，但在总体上齿轮间的摩擦力均呈现出先上升后下降到再上升的趋势.产生这种趋势的主要因素是齿轮的正压力.当齿轮转过的角度由5°转到10°时，轮齿进入单齿啮合区，该区域内的齿轮正压力逐渐增大，与此同时，轮齿间的摩擦状态由滑动摩擦变为静摩擦，摩擦系数也随之增大，从而使得摩擦力在该转角范围内急剧变大;当齿轮转过的角度由10°转到15°时，齿轮从单齿啮合区运行到双齿啮合区，该区域的齿轮正压力逐渐减小，摩擦状态又从静摩擦变回到滑动摩擦，摩擦系数也随之减小，导致齿轮摩擦力急剧变小，在剩余的转角范围内，由于齿轮正压力的再次增大，而摩擦状态却一直处于滑动摩擦状态，故摩擦力在该转角范围内的趋势有所上升但相对比较平缓.

2.4 转速对齿轮正压力、摩擦力的影响

针对图2、图3作进一步分析，将不同转速下同一啮合位置的齿轮正压力、摩擦力作为分析对象.由图2、图3可知:齿轮间的正压力、摩擦力随主动齿轮转速的增大而增大.但当齿轮处于转角为5°的啮合位置时，高速下齿轮的正压力、摩擦力明显小于低速和中速下的齿轮正压力、摩擦力.这是由于在高速的情况下，当齿轮的功率一定时，轮齿速度越大，齿面间产生的弹性变形越小，因此齿轮间的正压力、摩擦力就小.

3 结论

(1)虚拟样机技术可以实现对齿轮啮合过程的动力学仿真，仿真分析结果与理论计算结果基本吻合，表明齿轮的摩擦动力学仿真模型具有可靠性，同时该仿真方法具有很强的实际指导意义;

(2)对啮合过程中不同啮合位置的齿轮摩擦力进行仿真分析，得出:不同转速下的齿轮间摩擦力均呈现先上升后下降到再上升的趋势;

(3)应用虚拟样机技术仿真分析了主动齿轮转速对齿轮正压力、摩擦力的影响，同时得到了齿轮间的正压力、摩擦力随主动齿轮转速的增大而增大的规律;当齿轮处于转角为5°的啮合位置时，高速下齿轮的正压力、摩擦力明显小于低速和中速下的齿轮正压力、摩擦力.

［1］黄泽平，马吉胜，吴大林.齿轮轮齿接触力仿真研究［J］.机械传动，2007，31(2):26-28.

［2］李三群，贾长治，武彩岗，等.基于虚拟样机技术的齿轮啮合动力学仿真研究［J］.系统仿真学报，2007，19(4):901-904.

［3］刘涛，于化东，李一全，等.基于 CATIA和ADAMS的直齿圆锥齿轮建模与动力学仿真［J］.机械传动，2010，34(9):43-46.

［4］方子帆，舒刚，何孔德，等.齿轮传动多体接触动力学模型［J］.机械传动，2009，33(1):15-20.

［5］周旭辉，疏舒，马俊.基于ADAMS的小齿轮齿条动力学仿真分析［J］.船海工程，2012，41(5):119-121.

［6］机械设计手册编委会.机械设计手册单行本·齿轮传动［M］.北京:机械工业出版社，2007.

［7］成大先.机械设计手册:单行本.减(变)速器·电机与电器［M］.北京:化学工业出版社，2004.

［8］龙凯，程颖.齿轮啮合力仿真计算的参数选取研究［J］.计算机仿真，2002，19(6):87-88.

［9］石莹.机车牵引齿轮摩擦学性能研究［D］.大连:大连交通大学，2013.