白鹤电厂泵房进水间导流板倾角优化数值模拟
李家海, 桂林, 刘鹏
(四川大学水电学院, 四川 成都 610065)
白鹤电厂泵房进水间导流板倾角优化数值模拟
李家海, 桂林, 刘鹏
(四川大学水电学院, 四川 成都 610065)
基于Navier-Stokes方程和标准k-ε湍流模型, 采用非结构化网格和SIMPLEC算法对白鹤发电厂二期工程取水泵房进水间流道进行优化计算, 并对进水间前导流板角度变化时流态变化进行比较计算, 确定较优的导流角, 增强泥浆泵的排沙效果. 计算结果表明当前导流板角度为30o和后导流板角度为35o时有较好的流态, 此时流道底板附近流速较大, 并且整个流道内有较强烈的湍动流产生, 大部分泥沙可以达到冲淤平衡. 对多泥沙河流泵房取水间的设计、运行及维护有一定的参考价值.
数值模拟; 进水间; 导流角;模型
白鹤发电厂位于重庆市开县境内, 电厂一期工程装机100MW, 二期扩建装机2X300MW, 取水水源均为东里河. 二期取水口位于一期工程取水口上游约800m的右岸, 其取水泵房进水间共两个进水窗口, 相应有两个进水流道, 其进口宽度4706mm, 进口底板海拔高程172.20m, 水泵房布置四台16SAP-95A型水泵(流量为900-1260m3/h), 三台工作, 一台备用, 分别由两台水泵从一个进水间取水. 东里河河水中悬移质较多, 推移质较少, 平时河水清澈, 洪水时则河水浑浊. 河流洪水期含沙量较高, 取水泵房进水间水流流速慢, 容易造成泥沙淤积, 对发电厂正常工作造成了重大威胁. 本文采取优化水泵房进水间流道, 增加导流板的措施来减少取水间泥沙淤积量, 并通过数值模拟来比较改造前后的流道流态和改造后前导流板角度不同时的流态, 从而确定最优导流角[2]. 前导流板角度为30o进水间结构见图1.
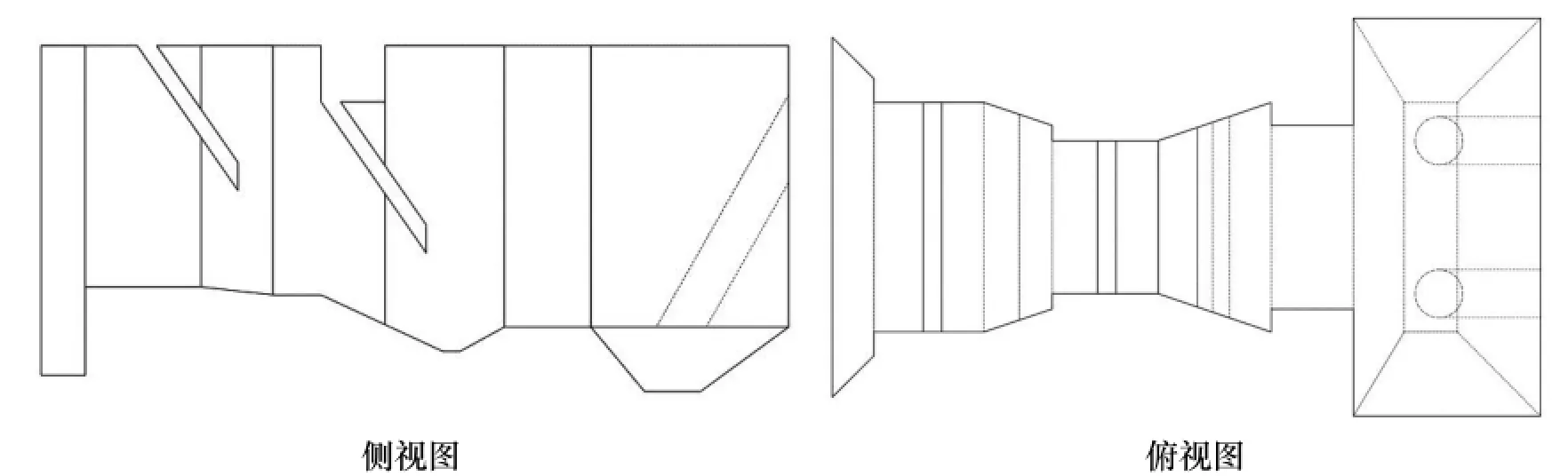
图1 前导流板角度为30o进水间结构Fig.1 The former guiding angle is 30owater channel structure
近年来, 计算流体力学(CFD)技术伴随着计算机技术的不断发展而逐渐成熟起来, 并被广泛应用到流场计算中. 本文取白鹤发电厂一个取水泵房进水间工作频率较高的某一工况(进水间水位高程为176.30m, 流量为1864m3/h)来进行数值模拟计算[3]. 分别对设计原型和改造后的三个不同前后导流板角度的模型进行了数值计算,并利用水力学知识进行比较分析, 以论证改造方案的可行性和确定最优导流角. 采用SolidWorks软件建立三维模型, 借助Gambit软件对模型流场进行网格划分和边界条件定义, 利用Fluent软件对四个不同的模型流道内部流场进行三维粘性流动数值计算, 得到了各个流道在不同流道结构和布置的流态, 利用水力学知识比较改造前
后的流态和比较不同导流角模型的流态. 本文对取水口的优化设计提供了一定的参考.
1 模型与计算理论
1.1 流体控制方程
本文用清水代替实际水流来进行计算, 并考虑到进水间水流速度慢, 水流液面变化很小的因素, 把取水口流道中的清水流动看作是非定常三维粘性不可压缩的液态单相流, 因此本文采用k-ε方程模型进行数值模拟,从而该流体满足如下流动方程组[4]:
连续性方程:

1.2 模型和计算网格
本模型是水泵取水间流道模型, 模型构建过程中忽略了拦污栅和进水间闸门的影响, 模型尺寸见表1.本文中计算模型流道内流体运动稳定性较差, 为了能顺利的对流场进行计算, 在划分网格时采用四面体和六面体网格[5]. 由于本文需要对三个模型进行计算并比较, 为了保证比较结果的准确性, 对三个模型的网格划分方式和大小保持一致性, 模型1网格划分见图2.
1.3 模型流道边界条件设置

图2 模型1的网格划分Fig.2 The mesh division of model 1

表1 模型尺寸Table 1 The size of model
进口: 速度进口(VELOCITY_INLET), 速度值为0.027m/s.
出口: 自由出流(OUTFLOW).
2 计算结果与分析
2.1 速度矢量图

图3 模型1速度矢量Fig.3 The velocity vector of model 1
由图3可以看出, 水流是呈现一个急剧压缩后急剧扩散的一个过程. 前导流板以下流道底板附近水流速度沿着水流方向逐渐增大, 但是在前导流板与后导流板之间流道底板附近水流流速逐渐减小. 此模型流道底板附近流速沿着水流方向变化较大, 泥沙在流速较大的地方不易沉积, 但是在流速减少的地方泥沙淤积比较严重,
并且水流与前导流板之间撞击和脱流比较严重.
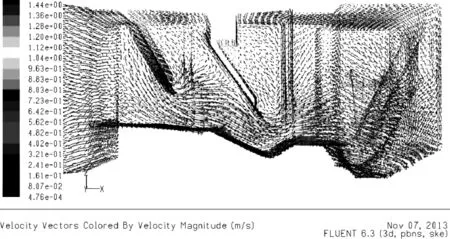
图4 模型2速度矢量Fig.4 The velocity vector of model 2
由图4可以看出, 水流在经过前导流板后, 流道底板附近流速大小分布比较均匀, 没有较大的变化, 能够较好的减少水流中泥沙在流道底板沉积. 水流与前导流板正面和背面接触较为平缓, 撞击和脱流现象不严重.
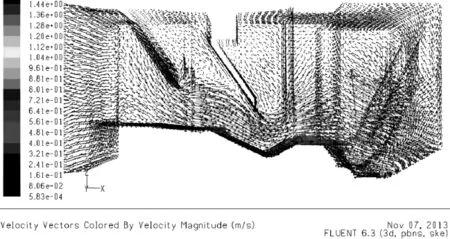
图5 模型3速度矢量图Fig.5 The velocity vector of model 3
由图5可以看出, 前导流板以下流道底板附近和前导流板与后导流板之间速度较小, 水流中泥沙容易沉积.
2.2 水流速度和湍动强度对比分析
取水泵房进水间的泥沙沉积程度与水流流态有较密切关系, 评估该种水力条件的重要参数是流速和湍动强度[6]. 在对进水间加装导流板之后, 在导流板处减小了过水断面的湿周, 增加了水力半径, 在相同的流量时, 该过水断面水流速度增大, 湍流强度增强, 并在导流板附近前后形成涡流, 减少了泥沙沉积量, 尤其是前导流板角度为30o时底板水流流速较大, 水流湍动较强烈, 有效的提高了取水泵房进水间的可靠性和经济性.
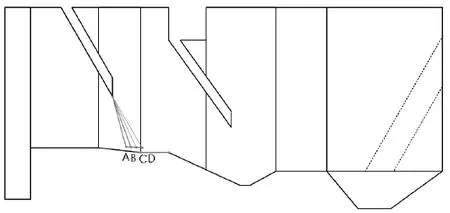
图6 模型比较取点位置Fig.6 The pointing position of model compare
为了比较模型前挡流板以下底板附近泥沙淤积程度, 并考虑到最优扩散角为15o, 取前导流板角度为30o模型底板附近的A、B、C、D四个点(如图6所示), 每个点所在线段与相邻之间夹角为5o, 距离进水间流道底板0.1m. 利用FLUENT的后处理功能, 分别获取各个模型在这四个点处的速度值和湍动强度值, 将其分别绘制到相应的两个图表上, 如图7和图8所示.
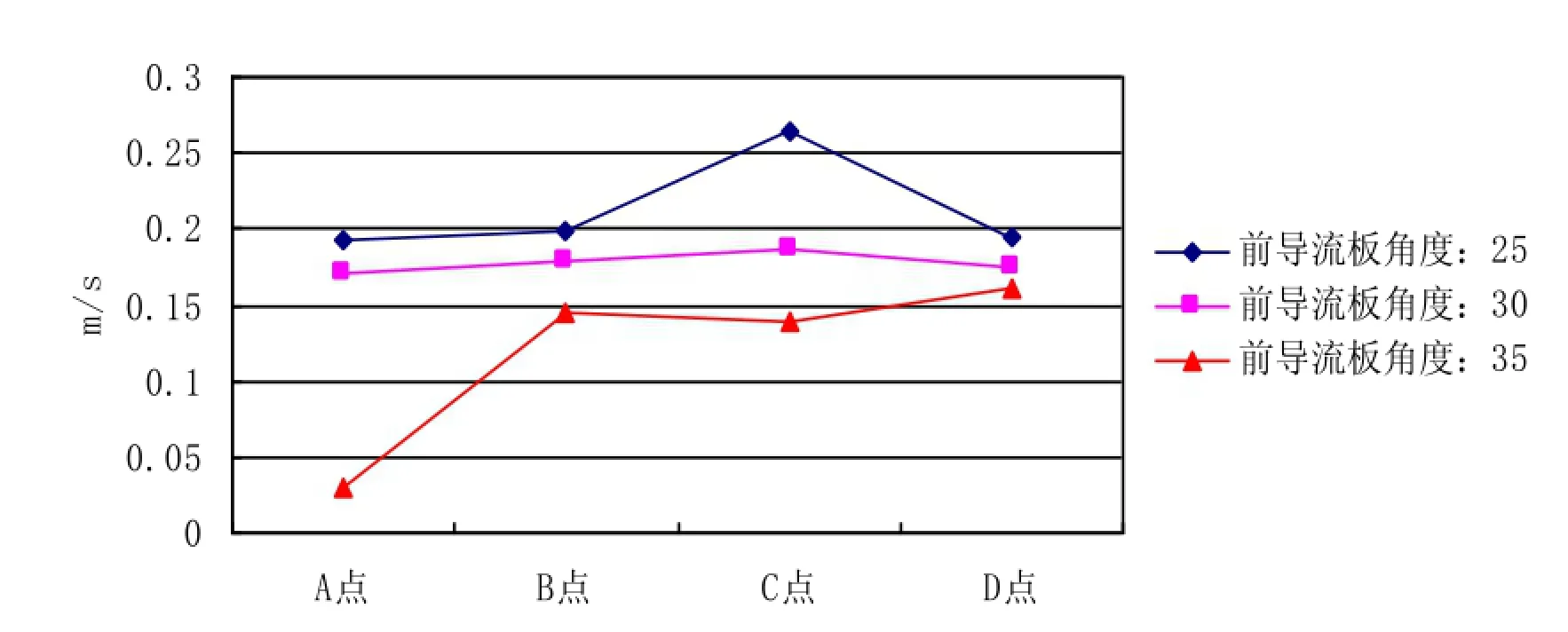
图7 A、B、C、D点流速分布图Fig.7 The velocity distribution of A,B,C,D
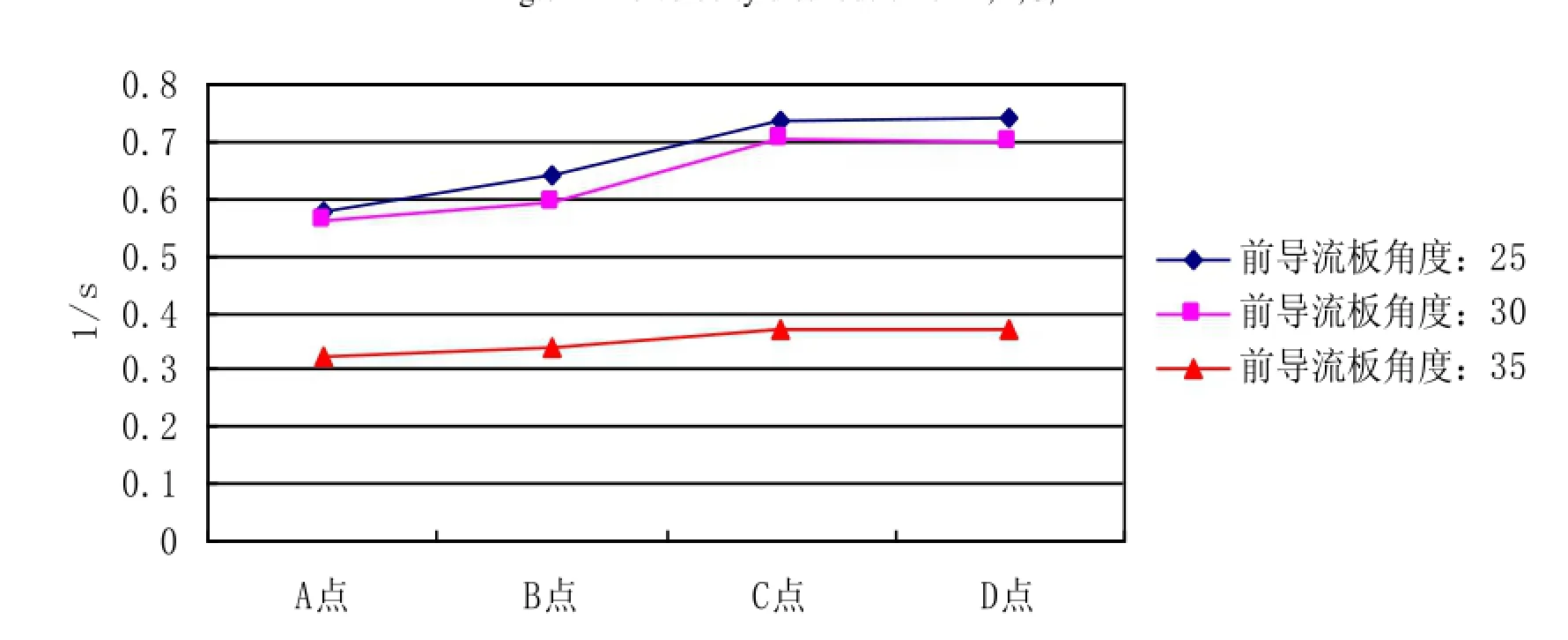
图8 A、B、C、D点湍动强度Fig.8 The turbulence intensity of A,B,C,D
如图7所示, 与另外两个模型流道相比, 前导流板角度为30o的模型2流道中A、B、C、D四点的流速值差
异并不大, 主要集中在0.15m/s和0.2m/s之间, 并且速度值变化较小, 而另外两个模型速度值有较大的变化.
如图8所示, 前导流板角度为30o的模型2流道中A、B、C、D四点湍动强度与模型1较为接近, 但是比模型3大很多. 综合考虑水流在模型流道中A、B、C、D四点处的速度值和湍动强度, 模型2流道中这几个点的水流运动程度都较剧烈, 泥沙淤积较少, 而模型1和模型3只是个别点处水流运动程度较剧烈, 由此可知, 前挡流板角度为30o时大部分泥沙可以达到冲淤平衡.
3 结论
本文为了对某发电厂取水泵房进水间导流板倾角进行优化设计, 分别构建了前导流板角度为25o, 30o和35o的三个流道模型, 采用Navier-Stokes方程、标准k-ε湍流模型、非结构化网格和SIMPLEC算法对三个模型进行数值模拟计算. 在对模型流道进行了流态比较和流速、湍动强度取点比较之后, 分析得出以下结果:
(1)水流取水泵房进水间流道进口处速度较慢, 在前导流板处速度迅速增大, 形成湍流, 减少泥沙沉积. 在后导流板处也有类似的效果.
(2)前导流板角度为30o的进水间流道底部附近流速比其他模型进水间流道底部附近有更好的分布, 不仅速度值较大, 而且范围广, 与此同时, 水流湍动强度也较高.
(3)计算成果表明前导流板角度为30o后导流板角度为35o为最佳组合.
(4)通过本文中对几个模型的计算得到了较符合实际的结果, 其与物理模型实验的结果较为接近. 由此表明,数值模拟方法不仅能够代替昂贵的物理实验, 而且可以得到较为可靠的数据.
[1] 王兰香. 同位网格SIMPLE 算法在水沙运动数值模拟中的应用[J]. 中国高新技术企业, 2011.
[2] 杨洪忠, 赖喜德, 张仁福. 水电站改造中的新技术[J]. 四川工业学院学报, 2004.
[3] 张利, 张鑫. 具有水室式调压室的引水发电系统调节保证计算及小波动稳定性分析[J]. 西南民族大学学报: 自然科学版, 2012, 38(5): 826-830.
[4] 王福军. 计算流体动力学分析—CFD软件原理与应用[M]. 北京: 清华大学出版社, 2006.
[5] 韩占忠, 王敬, 兰小平. FLUNT流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2005.
[6] 陈建, 李义天, 邓金运, 等. 水沙条件变化对三峡水库泥沙淤积的影响[J]. 水力发电学报, 2008.
The numerical simulation study on the optimum design about water channel guiding angle of Pump House of Baihe Power Plant
LI Jia-hai, GUI Lin, LIU Peng
(School of Water Resource & Hydropower, Sichuan University, Chengdu 610065, P.R.C.).
This paper, based on the Navier-Stokes equations and the standard k- ε turbulence model, uses unstructured gridand SIMPLEC algorithm to optimize and calculate the water intake pump house water channels of second phase project of Baihe power plant, compares the calculation of the flow regime when the former guiding angle is changed, explores a better guiding angle and enhances the desilting effect of mud pump. The calculation results show that when the former guiding angle of30oand the hind guiding angle of 35ohave better flow regime, velocity near the flow channel floor is larger, and the entire flow is relatively strong turbulent flow in the water channel, most of sediment erosion and deposition can reach a balance.
numerical simulation; water intake house; guiding angle;model
TV214
: A: 1003-4271(2014)03-0415-06
10.3969/j.issn.1003-4271.2014.03.17
2013-12-19
李家海(1986-), 男, 四川古蔺人, 硕士研究生, 研究方向: 水电站水力学及动力系统, E-mail: 331701726@qq.com.通讯作者:桂林(1963-), 男, 副教授, 研究方向: 水电站水力学及动力系统.

