基于切比雪夫不等式的输变电工程造价合理区间的计算方法
张戈力,温卫宁,李培栋,任 妍,卢 玉,商 桑
(国网北京经济技术研究院,北京市102209)
0 引 言
根据我国电网的发展规划,电网企业将加快建设坚强智能电网,全力推进重点工程建设,以提高电网智能化水平。为了适应新的工程建设,保障项目建设顺利开展,研究与之有关的造价水平的合理性分析方法,保障造价管理精益化水平不断提高,对于电力企业的项目决策和社会经济资源的合理利用都具有重要的理论和实践意义。
在基建项目中,造价管理水平的高低直接决定着投资效益。现行的造价管理方法虽已较为完善,但在项目的规划论证及技术经济分析领域仍有一定的提高空间,缺少以数学理论及大量工程实际数据为基础的定量分析依据。
电网基建工程的造价水平受到物价上涨、政策调整等方面影响会有一定上涨[1],工程造价会出现一定变化,合理的工程造价水平是影响电力建设健康发展较为关键的因素,因此,控制电网工程造价水平的问题显得较为突出[2]。
目前,电网工程造价水平分析方面的成果主要有:文献[3]根据电网工程限额设计指标,对220 ~750 kV 电网工程做了分析;文献[4]采用输变电工程通用造价分析方法,对110 ~750 kV 电网工程进行分析等。这些方法以技术条件为计算基础,较为贴近实际工程,在项目论证、经济评价、造价管理等方面被广泛地应用。
文献[5]指出受到经济条件、设备材料价格、建设外部环境影响,电网工程的造价是不断变化的,应作较为深入的分析,为有效控制工程造价提供参考。处于不同地区的电网工程造价水平波动应在一定合理范围内。掌握造价的合理范围,可以直观表现电网工程造价特性。合理区间可以作为工程前期论证的决策参考,指导工程造价工作,为多角度定量分析造价提供了新的方法。目前,尚未有一种深入分析造价合理区间的计算方法。
为此,本文提出造价合理区间的概念并给出其计算方法,基于可靠数据,该方法可以实现对全电压等级造价合理水平的分析,具有较强的可用性。
1 输变电工程造价的合理区间
1.1 造价合理区间的定义
分析输变电工程中各电压等级变电、线路工程的样本数据时,为了得到一个具有代表性的造价合理水平区间作为造价控制的参考指标,根据相关专家经验,定义使得大部分(频数占总数至少80%)造价样本数据落入的集中分布区间φ 为输变电工程造价的合理区间,代表该地区这一电压等级待建工程造价合理水平。
该造价合理区间指标可作为初步判别工程投资的依据,也可为制定投资计划提供参考依据等,实现工程造价控制的可控、在控的要求。
1.2 造价合理区间的计算思路
论文提出的造价合理区间的计算分为3个步骤,包括样本数据的特征值计算,采用箱线图剔除样本异常值[6],根据切比雪夫定理[7]、单变量最优化法[8-9]计算造价合理区间。
统计输变电工程中各电压等级的变电、线路的工程总投资,根据总容量或总长度数据分别计算单位容量造价和单位长度造价,作为造价合理区间计算的原始样本数据。
将变电、线路工程的数据样本按照“电压等级”、“所在地区”两个条件进行划分,其中线路工程分为“单回”和“双回”两种情况分析,如图1 所示。
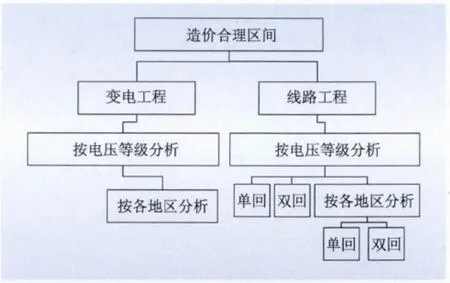
图1 造价数据分析的分类方法Fig.1 Classification of cost data analysis
2 工程造价合理区间的计算方法
2.1 计算步骤
(1)计算该样本数据的中位数、第一四分位数、第三四分位数,分析得到样本数据的最大值、最小值,计算样本数据的样本均值、样本方差[10]。
(2)采用箱线图剔除异常值,对造价数据进行一次异常值分析,排除异常值以后,样本数据将减少,样本数据将更趋于合理,为下一步计算区间提供基础数据。
(3)根据切比雪夫不等式原理,有至少80%的统计数据落在区间φ 中,即
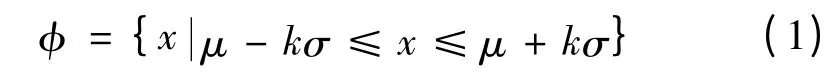
式中:μ 为样本的平均值;σ 为样本标准差;k 为区间系数。
此时k =2.24,将k 值作为造价合理区间的系数初值,利用一维参数寻优中的进退法迭代计算k 值的最优值,最终确定造价合理区间。
2.2 箱线图
异常值是指样本中的个别值,其数值明显偏离其所属的其余观测值[11]。因为数据中的异常值常会对数据的计算带来较大的拉动作用,如果不进行异常值筛选,分析结果有较大可能会偏离正常水平,所以应在分析计算之前筛除异常值。
箱线图是由1 组数据的最大值、最小值、中位数和2个四分位数这5个特征值绘制而成的、反应原始数据分布的图形。箱线图提供了识别异常值的标准:异常值被定义为小于下四分位数QL减去1.5 倍四分位距离QIQR、大于上四分位数QU加上1.5 倍四分位距离QIQR,即Q <QBL或者Q >QBU,其中

箱线图判断异常值的标准以四分位数和四分位距离为基础,因为四分位数是一个固定位置的数据值,不容易受到数据异常变化的影响,异常值不能对这个标准施加较大影响。
在筛除了对样本均值、样本方差拉动作用较大的异常值后,再计算样本均值及样本方差得到的分析结果更能反映样本数据的数理特点。
2.3 根据切比雪夫不等式确定k 值初值
对于任意分布形态的数据,根据切比雪夫不等式,至少有C 组数据落在k个标准差之内。切比雪夫不等式不要求明确样本数据的分布情况,能够确定数据所占百分比例C 的下限,样本数据落入均值周围k倍标准差[10],即区间的百分比例至少为

由式(3)得到样本值落入区间的百分比例,结果如表1 所示。
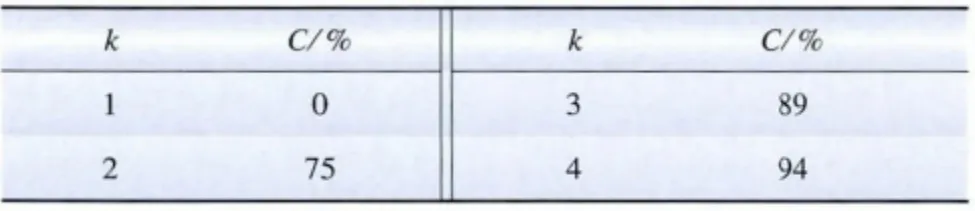
表1 样本值落入区间的预测比例值Tab.1 Prediction ratio of sample values located in interval
由表1 可知:当C =80%时,即至少有80%的数据样本落入区间时,系数k =2.24。如计算得到的区间包括了80%以上样本数据,则可以通过调整系数k的值,使得造价区间趋于包括80%左右的样本数据,即本文所提出的造价区间。
2.4 基于进退法参数寻优的合理区间计算
参数寻优方法较多,包括黄金分割法、割线法、抛物线插值法[12-14],本文以一维参数寻优方法中的进退法为基础,计算合理区间中的参数k。
进退法的计算思想是先从初值λ0出发,利用目标函数F(λ)的信息,来回仔细地搜索,以期求得无条件极值问题、即minF(λ)的最优解。进退法计算步骤如图2 所示。

图2 造价合理区间的系数k 值的调整计算过程Fig.2 Calculation process of k adjustment in reasonable interval
计算造价合理区间,即是计算当λ0= k 时,使得
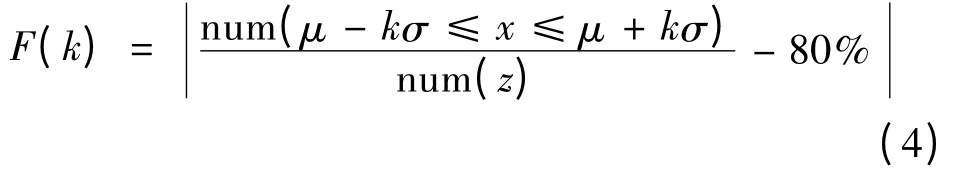
有最小值。
3 合理区间的算例分析
3.1 样本数据
以A、B 两个地区的35 kV 变电工程为例,做造价合理区间的算例分析,两个地区分别有10个工程造价样本,分别为x1i,x2i,单位为元/(kVA),如表2所示。其中A 为中国内陆省份,B 为中国沿海省份,B 地区较A 地区经济更为发达。
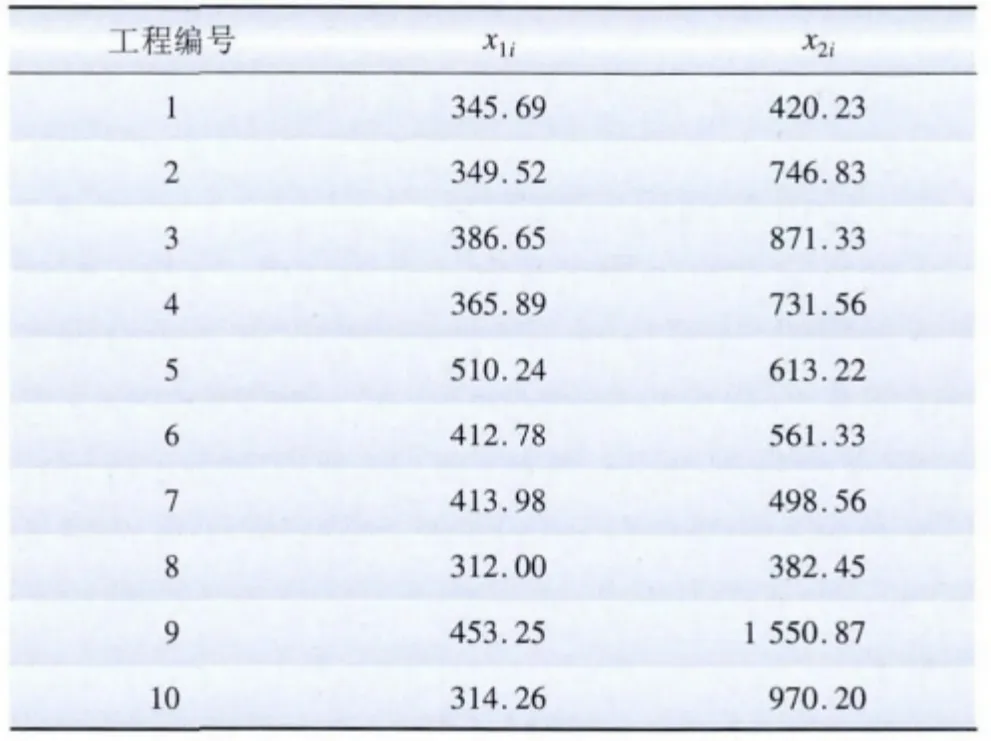
表2 某35 kV 变电工程单位造价样本Tab.2 Unit cost sample of a 35 kV substation元/(kVA)
3.3 算例计算
计算样本的中位数、第一四分位数、第三四分位数,分析得到样本数据的最大值、最小值,计算样本数据的样本均值、样本方差,结果如表3 所示。
计算箱线图的上、下限,得到的结果如表4 所示。由表4 可知:x29=1 550.87 超出了上限值,不在箱线图正常数据的范围之内。该项工程因为建在特殊地域,项目的建设场地征用费等其他费用占总体造价的比重较高,因此拉高了总造价。如果加入合理区间的计算当中,将对计算结果起到较大的拉动作用。
对比分析剔除异常值前、后的样本均值和样本方差,结果如表5 所示。

表4 箱线图上下限Tab.4 Upper and lower limit of boxplot元/(kVA)

表5 异常值的影响Tab.5 Influence of outliers
分析可知,该样本对于样本方差的影响达到了41.86%,对样本方差有较大的拉动,使得计算结果偏离了合理水平。经过分析,x29属于异常数据,应予剔除。
根据切比雪夫不等式确定初值区间,代入计算得到的样本方差和样本均值,得到A 地区及B 地区的初值区间φ1、φ2为
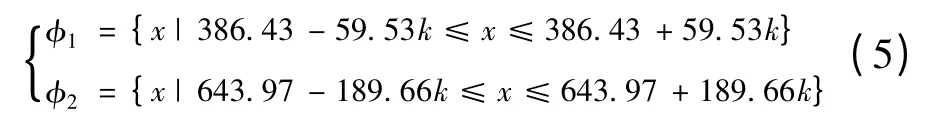
则有:
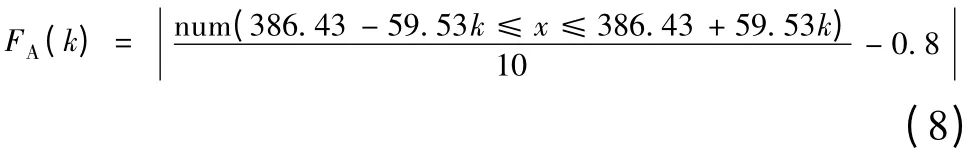
求可使FA(k)取最小值的k 值。
设初始步长h0= -0.1,ε=0.005,k0=2.24。利用进退法计算k 值,A 地区的计算结果如表6 所示。
由表6 可知,当迭代计算到16次时,步长|h| <ε,计算终止,得到kx1=1.215 0,计算得到造价合理区间为:φ1={x|314.10≤x≤458.76}。
同理可计算得到B 地区的计算结果如表7 所示。由表7 可知,当迭代计算到9次时,步长|h| <ε,计算终止,得到kx2=1.383 7,计算得到造价合理区间为:φ2={x|381.52≤x≤906.41}。
3.4 结果验证及分析
算例计算得到的合理区间φ1、φ2分别包含了样本A、B 中的8个样本,占总样本数的80%,符合论文对于合理区间的定义。
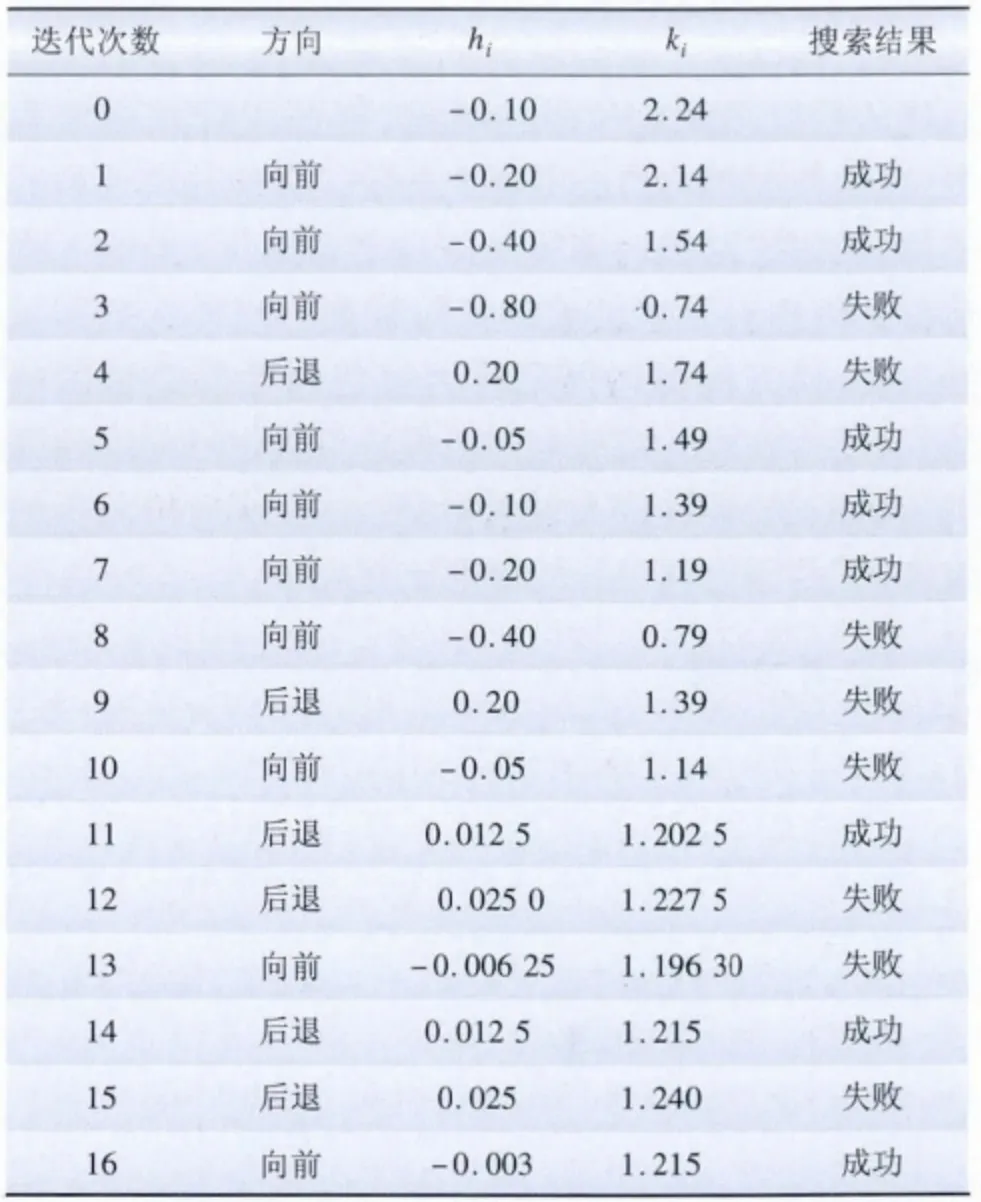
表6 A 地区参数寻优计算Tab.6 Parameter optimization calculation of Area A
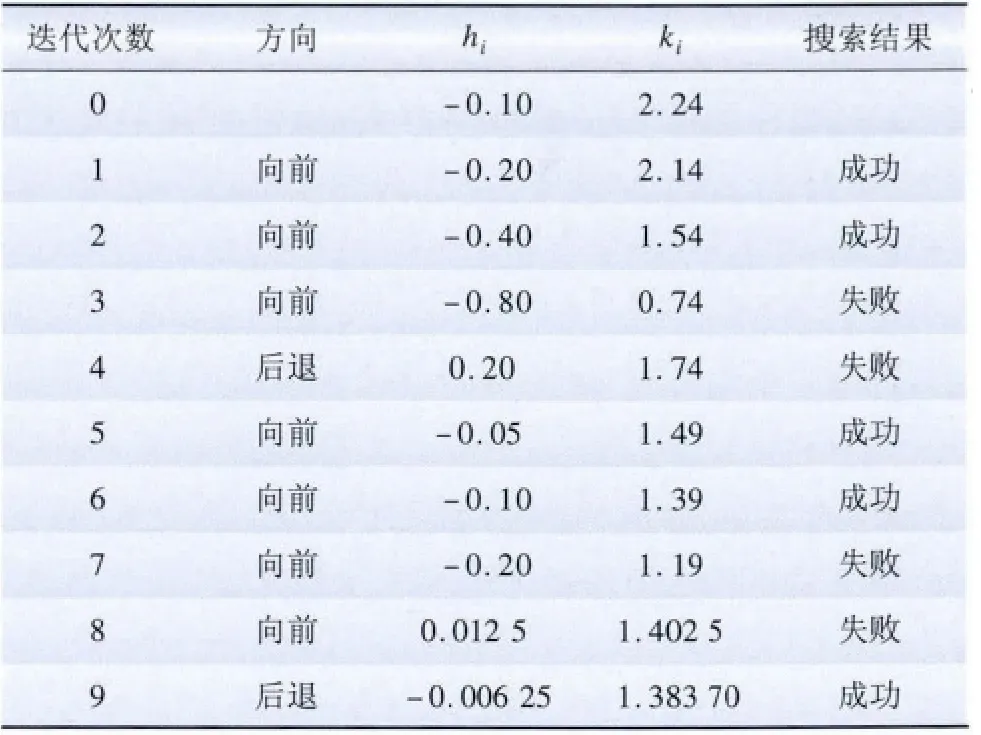
表7 B 地区参数寻优计算Tab.7 Parameter optimization calculation of Area B
由于B 地区处于沿海发达地区,线路、变电工程造价中建设场地费用占总造价的比重较大[15],相应的造价水平也相对较高,φ2的单位容量造价水平较φ1更高一些,合理区间计算的结果也反映了这一情况。
4 结 论
在实际的工程决策、工程评审中,造价区间可以作为参考指标,用2个地区的造价合理区间的算例分析说明了论文方法的应用。本文定义了工程造价合理区间,提出了一种合理区间计算方法,该方法首先运用的箱线图优化了原始数据,提高了计算可信程度,然后依据切比雪夫不等式确定了寻优迭代计算的初值,利用进退法计算得到造价合理区间,降低工程造价工作中对专家经验的依赖程度。当样本数据足够大时,该方法可以得到较为有代表性的造价区间值,可以为该地区控制电网工程造价提供可靠度较高的分析依据,具有较大的实际意义;扩展造价分析的维度,有利于电网工程的标准化建设。
[1]李新华.对电力工程造价控制的探讨[J].电力建设,1997,18(9),63-65.
[2]刘华敏,杨丽霞,肖红. 电力工程造价的管理和控制[J]. 电力建设,2001,22 (3):64-66.
[3]电力规划设计总院.电网工程限额设计控制指标(2012年水平)[R].北京:电力规划设计总院,2013.
[4]刘振亚.输变电工程通用造价[M].北京:中国电力出版社,2010:1-11.
[5]贾平俊.统计学[M].北京:清华大学出版社,2004:95-96.
[6]史雪飞,赵彪,陈立,等.2010年输变电工程造价分析[J].能源技术经济,2012,24(4):44-47.
[7]庄作倾.Box Plot-描述统计的一个简便工具[J]. 统计与预测,2003(2):56-57.
[8]朱丰,柏又青,冯有前,等.一种针对收敛性问题的改进进退法及其仿真验证[J]. 空军工程大学学报:自然科学版,2010,11(2):86-90.
[9]史清录,孔祥莹,康健.进退法在多维非线性有约束优化问题中的应用[J]. 太原重型机械学院学报,2001,22(8):200-203.
[10]李心渝.应用经济统计学[M].北京:北京大学出版社,1999:67-85,88-89.
[11]GB/T 4883—2008 数据的统计处理和解释 正态样本异常值的判断和处理[S].北京:中国计划出版社,1985.
[12]吴新元.改进割线法及其大范围收敛性[J].南京大学学报:自然科学版,1994,30(4):583-588.
[13]宋巨龙.利用平面上的黄金分割点法求全局最优解[J]. 数学实践与认识,2004,34(11):113-117.
[14]程远楚.水轮机瞬变过程计算的改进抛物线插值法[J]. 水电站设计,1997,13(1):57-61.
[15]郑燕,宋毅.线路工程建设场地征用与清理情况现状分析[J]. 电力技术,2010,19(7):50-52.

