基于最小二乘综合权重优化模型的风电场电能质量评估

杨 梅，周喜超

(1．甘肃省电力设计院，兰州市730050;2．国网节能服务有限公司，北京市100052)

0 引 言

随着风力发电规模的不断升级，风电渗透率越来越高，风电场的并网运行对电网电能质量的负面影响也随着风电场规模的扩大而成为人们日益关注的重点［1-5］。随着用户侧对电能质量要求越来越高以及敏感性负荷设备的日益增多，如何对用电质量进行综合评价逐渐成为现代电力系统一项重要的研究内容。

风电场电能质量的评估是一个基于多指标的综合性评估问题，如何科学合理地选择指标及确定指标权重，直接关系到风电场电能质量综合评估结果的正确性以及后续的治理方案。电能质量评估不当，将付出巨大的人力和经济代价［6］。目前，确定电能质量指标权重的方法大致可以分为2 类:主观赋权法和客观赋权法。主观赋权法的特点是能较好地反映评价对象所处的背景条件和评价者的意图，体现了决策者的经验判断;其缺点是权重的确定与数字特征没有关系，忽视了评价指标之间的联系，并且各个指标权重系数的准确性直接取决于评价者的经验和知识［7］。客观赋权法完全不依靠评价者的主观判断，只根据原始数之间的数字特征来确定权重，因此评价结果有很强的数学理论依据［8］。但是，客观赋权法却忽视了专家的知识与经验等，因而通用性和决策人的可参与性较差，在实际运用中确定的权重常常会和评价指标的实际重要程度相反［9］。

考虑到客观或主观赋权方法的局限性，本文提出了一种基于最小二乘综合权重优化模型，既避免了利用客观赋值得到的权重系数不合理的现象，又避免了层次判断矩阵主观随意的缺点。最后，通过对昌马西风电场4个母线电能质量测量点的综合评估，验证了该模型的合理性。

1 层次分析法的标准评估方法

层次分析法(analytical hierarchy process，AHP)是一种多准则决策方法，它结合了定量与定性分析，同时结合了人的经验判断以及严格的数学理论，因此可以比较有效地测评决策者的判断，分析目标体系层次间的非序列关系［10-12］。其算法的基本步骤如下所述。

(1)判断体系中各对象的相互关系，构建递阶层次结构。

(2)对处于同一层次的各对象关于上一层次中某一要素或准则的重要性进行相互比较，在此基础上构造判断矩阵M，其元素取值根据Saaty 的1 ～9 标度法选择，如表1 所示。

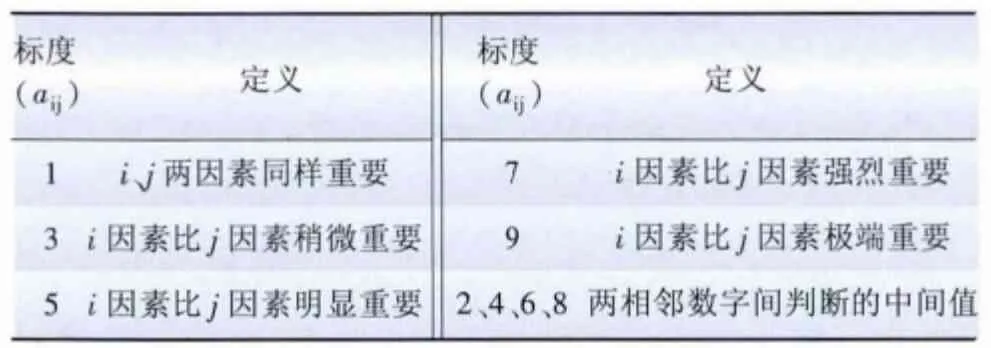
表1 判断矩阵元素含义Tab.1 Elements meaning of judgment matrix

(3)对构造的矩阵M 进行一致性检验，从而保证所构造判断矩阵的正确性，并计算单层权重向量。

CI 表示评价判断矩阵的一致性指标:

式中:λmax为M 的最大特征值。CI 值越小，判断矩阵的一致性越好，CI =0 时，矩阵M 具有完全一致性。随机一致性比率CR 等于判断矩阵的一致性指标CI与同阶平均随机一致性指标RI 的比值:

当CR≤0.1 时，判断矩阵通过一致性检验，否则需要调整aij值，重新构造判断矩阵。

计算得到判断矩阵的最大特征值，并求出其对应的特征向量Q=［q1，q2，…，qn］，则有:

将特征向量Q 进行归一化，得到单层权重向量

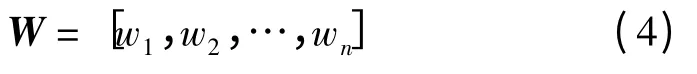
(4)综合单层权重向量计算综合权重向量。

(5)按综合权重向量对评价系统的方案进行排序。

AHP 的评估过程是把复杂问题分解成各个组成因素，按因素间的支配关系建立层次结构模型。针对本层次任意2个因素间，上一层次某因素的相对重要性，构造判断矩阵得到相对重要度。最后经过单层排序和总排序决策判断，确定最低层各方案相对于最高层目标的最优程度排序［13-14］。在上述确定权重系数的过程中，由判断矩阵决定权重向量的方法实际上是一种主观赋权法，体现了决策者的经验判断，并且只靠决策者的知识来确定评价对象的重要性排序从而确定权重。而客观赋权法［15-16］却只依赖于数据信息，虽能有效传递评价指标的数据信息和差别，但由于忽视了专家的知识与经验积累，在实际运用中确定的权重常常会和评价指标的实际重要程度相反。因此本文提出基于最小二乘综合优化的指标权重模型，使层次分析法在客观赋值法下进行改进以实现两者的有机统一。

2 基于最小二乘综合权重优化模型

设由判断矩阵确定的主观指标权重系数为

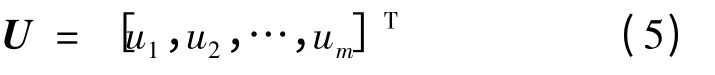
由变异系数法确定的客观指标权重系数为

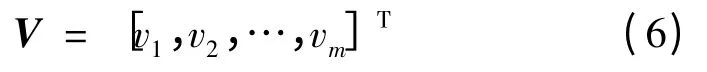
基于最小二乘综合优化之后的指标权重系数为

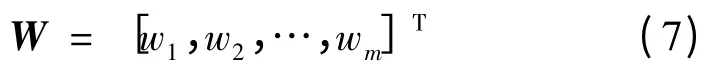
设待评估对象有n个，评估指标有m个，则标准化后的测量数据矩阵为Z = (Zij)n×m。其中，第i个评估对象的评估值为

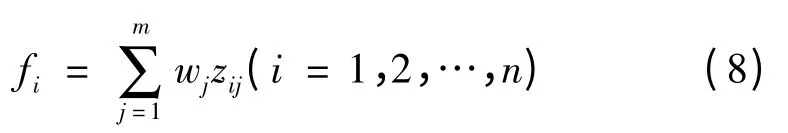
层次分析法确定的评估对象的所有指标的评价值偏差应当越小越好，为此建立如下最小二乘法综合评价模型。

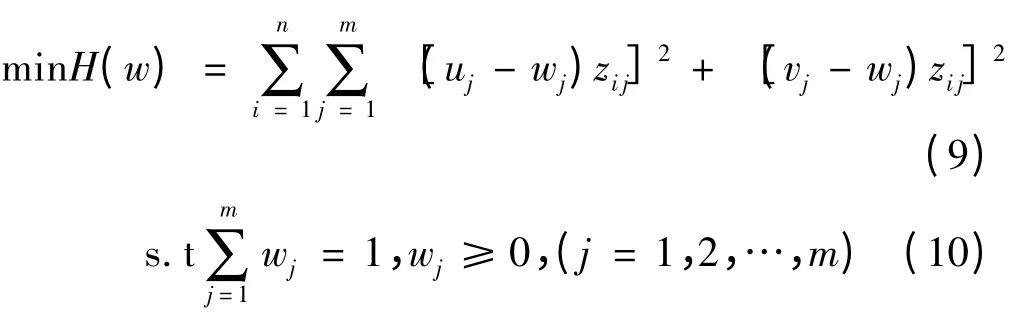
构造一个拉格朗日函数对条件极值进行求解:

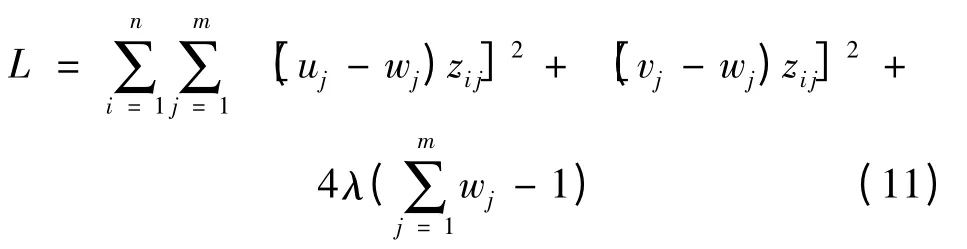
拉格朗日函数求偏导:

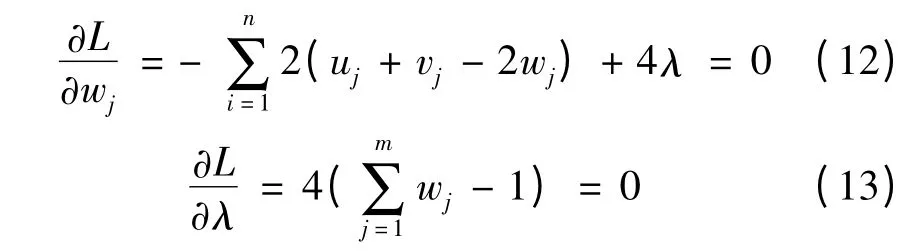
转换成矩阵形式:

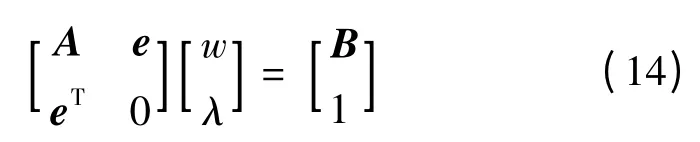
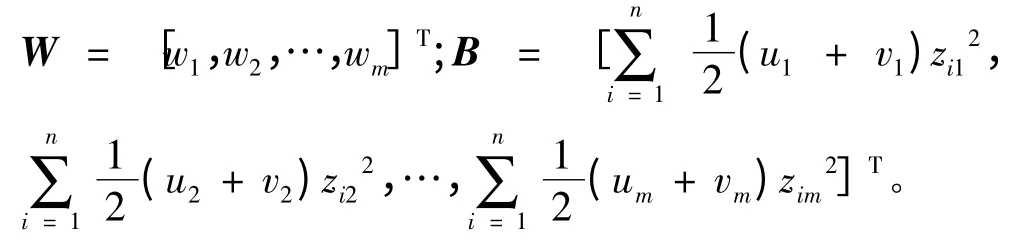
因此，可解上述矩阵，得到综合优化权重系数为

由上述构建过程可以看出，最小二乘综合优化之后的指标权重系数综合了主观赋权法和客观赋权法的特点，通过降低评价值的偏差实现了2 种赋权方法的有机结合。

3 实例分析

3.1 电能质量评估等级划分

本文将电能质量评级标准划分为8个级别，合格范围内的为5 级，不合格范围的为3 级。其中不合格范围的指标数值跨度为合格范围内的2 倍，这样有利于细化考量合格范围内的电能质量，粗略考察不合格范围的电能质量。电能质量考察指标分别为电压正负偏差绝对值ΔU、谐波电压总畸变率THD、奇次谐波畸变率HRU、三相不平衡度εU、频率偏差Δf 和短时间电压闪变Ut，具体划分方法如表2 所示。

3.2 昌马西风电场

昌马西风电场位于甘肃酒泉风电基地，共有3 座50 MW 风电场，3 座风电场均采用东方汽轮机厂的FD82 双馈风机，每台风机均经过机旁的箱式变压器升压至35 kV 后，汇入35 kV 母线后分别由3 台35/363 kV 主变汇至330 kV 母线由玉昌线送出。分别对35 kV 电压等级的母线1、母线2、母线3 和330 kV 母线4 的电能质量进行测量。该风电场接线图及电能质量监测点位置如图1 所示。

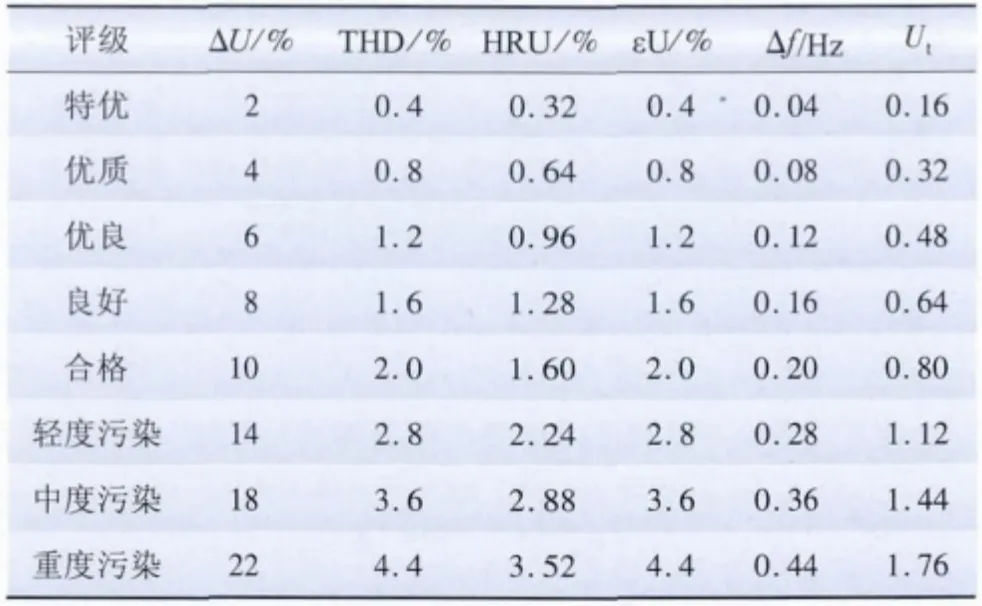
表2 电能质量等级划分方法Tab.2 Power quality grading method

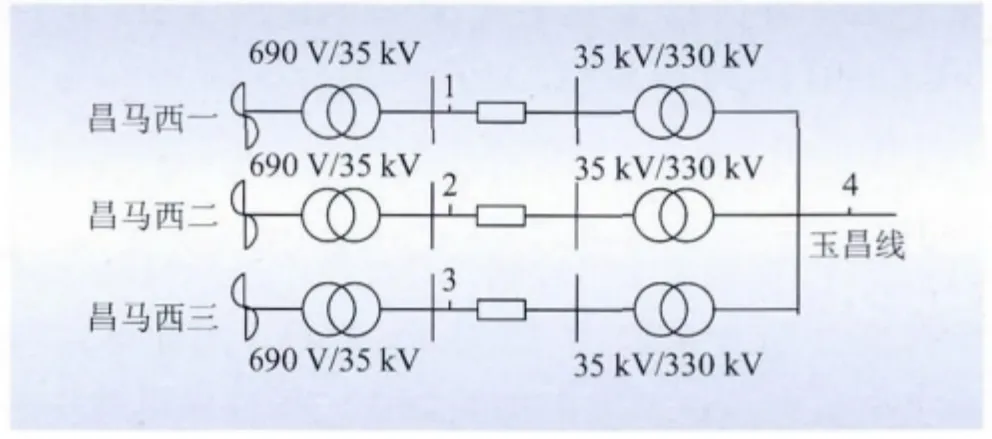
图1 昌马西风电场接线图及电能质量监测点Fig.1 Wiring diagram and power quality monitoring points in ChangMaxi wind farm

3.3 昌马西风电场电能质量综合评估

监测母线电能质量指标电压偏差、电网谐波含量(包括总畸变率THD、三次谐波含有率HRU3、五次谐波含有率HRU5 和七次谐波含有率HRU7)、电压波动闪变值Ut、三相不平衡度εU、频率偏差Δf 的监测数据如表3 所示。

构建昌马西风电场电能质量评估模型如图2所示。

首先，根据层次分析法确定权重系数，根据专家确定的电能质量指标相对重要程度构造判断矩阵，得到主观权重系数为U =(0.34 0.067 0.02 0.04 0.03 0.16 0.26 0.088)。

其次，采用变异系数法求得35 kV 电压等级的客观权重系数为V = (0.003 0.09 0.24 0.004 0.055 0.24 0.13 0.21)。

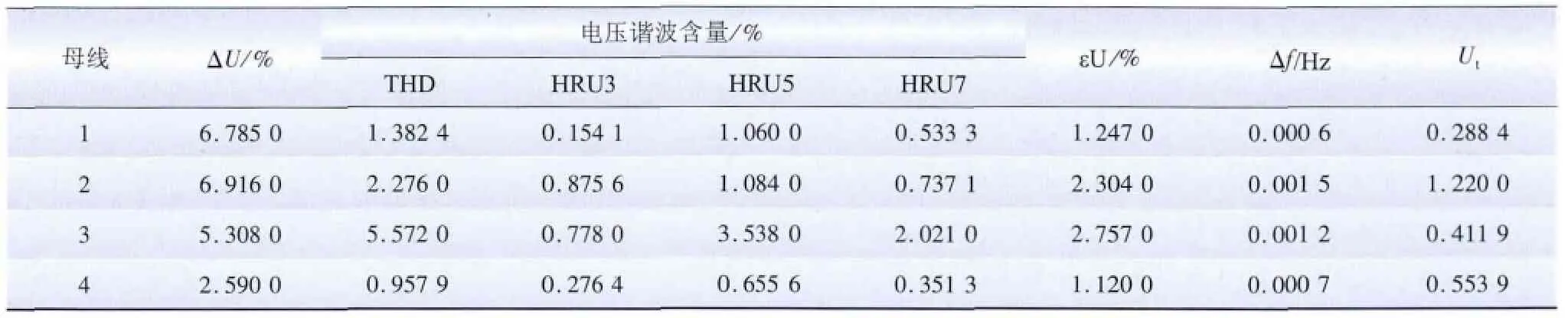
表3 昌马西母线监测点电能质量数据Tab.3 Power quality at busbar monitoring points in ChangMaxi wind farm

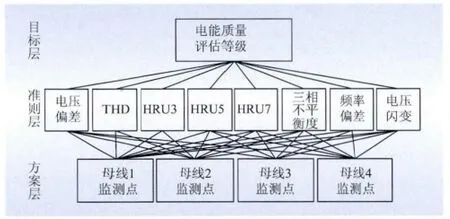
图2 昌马西风电场电能质量评估模型Fig.2 Power quality assessment model for ChangMaxi wind farm

再次，利用最小二乘综合权重优化模型得到电能质量综合评估权重系数为W = (0.17 0.075 0.13 0.02 0.04 0.20 0.197 0.15)。

最后，对单层权重系数进行综合，计算层次总权重系数，按层次总排序重要性系数对评价系统的方案进行排序，得到4个待评估点母线的电能质量综合评价数值分别为0.52，0.23，0.27，0.49。因此可以得到4个监测点母线的电能质量优先等级为母线1 ＞母线4 ＞母线3 ＞母线2。

对比表2 电能质量等级划分数据可以得到昌马西母线监测点电能质量评估结果:母线1，优良;母线2;轻度污染;母线3，轻度污染;母线4，优良。对比表2 和表3 可以看出，母线1 和母线4 的8 项测量指标均合格，在实际仿真中，母线1 和母线4 所接负荷均为线性负荷，即电能质量综合评估结果为优良;母线2 大部分的测量指标均合格，不过由于电力机车、闪变源及不对称负荷的存在，使得其THD、εU 和Ut超出国家标准，因此电能质量综合评估结果为轻度污染;同理，由于不对称负荷和整流装置的存在，母线3的THD、HRU5 和εU 均超标，因此电能质量综合评估结果为轻度污染。因此，结合上述仿真结果和电力系统实际运行条件可知，4条母线的电能质量综合评估结果是正确合理的。

4 结 语

针对主观或客观赋权方法的局限性，本文提出基于最小二乘综合权重优化模型用于风电场电能质量的综合评估。通过构造基于最小二乘法的综合评价模型和拉格朗日函数对条件极值进行求解，实现了层次分析法在主观赋值和客观赋值法的有机统一。通过对电能质量评级标准划分等级和基于该模型对昌马西风电场四条母线的电能质量监测数据进行了综合评估，评估结果正确合理，从而验证了本文提出模型的正确性，为风电场电能质量评估提供了一种科学有效的方法。

［1］Chen C L，Lee T Y． Impact Analysis of Transmission Capacity Constraints on Wind Power Penetration and production cost in generation dispatch ［C］//IEEE International Conference on Intelligent Systems Applications to Power Systems，Taibei，China:IEEE，2007:1-6．

［2］雷亚洲，王伟胜，印永华，等． 一种静态安全约束下确定电力系统风电准入功率极限的优化方法［J］． 中国电机工程学报，2001，21(6):25-29．

［3］张国新．风力发电并网技术及电能质量控制策略［J］． 电力自动化设备，2009，29(6):130-133．

［4］王海云，王维庆，梁斌．风电场在公共连接点的闪变［J］． 电力自动化设备，2008，28(12):81-83．

［5］樊宝龙．STATCOM 抑制并网风电机组电压波动的研究［D］． 秦皇岛:燕山大学，2011．

［6］孟婷．电能质量综合评估方法研究及系统开发［D］．长沙:湖南大学，2012．

［7］毛定祥．一种最小二乘意义下主客观评价一致的组合评价方法［J］． 中国管理科学，2002，10(5):95-97．

［8］陈顺怀，冯恩德，王呈方．闭区间数多属性决策方法［J］．武汉交通科技大学学报，1999(3):267-269．

［9］蔡红军． 武川风力发电场电能质量综合评估及治理措施研 究［D］．保定:华北电力大学(保定)，2011．

［10］Hosten C，Fidan B． An Industrial Comparative Study of Cement Clinker Grinding Systems Regarding the Specific Energy Consumption and Cement Properties ［J］． Powder Technology，2012 (221):183 –188．

［11］吴琼．风电场对电网电能质量影响的研究［D］． 南昌:南昌大学，2008．

［12］Khurana S， Banerjee R， Gaitonde U． Energy Balance and Cogeneration For a Cement Plant ［J］． Applied Thermal Engineering 2002，22(5):485 –494．

［13］Ansari N，Seifi A． A System Dynamics Model for Analyzing Energy Consumption and CO2Emission in Iranian Cement Industry under Various Production and Export Scenarios ［J］． Energy Policy，2013 (58):75 –89．

［14］娄素华，李志恒，高苏杰，等．风电场模型及其对电力系统的影响［J］．电网技术，2007，31(增刊2):330-334．

［15］Tande J O G． Impact of wind turbines on voltage quality［C］//The 8th International Conference on Harmonics and Quality of Power ICHQP’98，Athens:IEEE，1998:14-16．

［16］Grandhare W Z，Bhagwatikar G R． Power Pollution due to Connected Wind Electric Converter［C］//International Conference on Control Applications，Anchorage，Alaska，USA:IEEE，2000:892-895．