覆冰导线空气动力系数数值分析

刘振宇

(北京国网富达科技发展有限责任公司，北京市100070)

0 引 言

覆冰导线的气动力是舞动的激励源，是舞动激发最直接的决定因素，而气动力的变化主要取决于覆冰导线空气动力参数的特性，因此覆冰导线气动力参数是导线舞动的关键因素，需要开发有效的方法研究其特性为舞动的理论分析提供初始输入条件。自1974年以来，国内外学者对覆冰导线气动力特性进行了大量试验研究［1-9］，其中D 型和新月型这2 种形式的覆冰研究较为成功，但是目前还缺乏非稳态条件下覆冰导线动力特性的研究。同时由于覆冰形状、导线型号、覆冰厚度及来流风速的多样性，风洞实验研究代价巨大，仅靠风洞试验提供覆冰导线的空气动力学参数是不实际的，因此采用数值模拟的方法研究覆冰导线空气动力特性，已经引起重视并开展了相关分析。蔡萌琦等［10］采用流体动力学分析软件计算了典型覆冰四分裂导线在特定风速下的绕流问题。林巍等［11］计算了新月形薄覆冰单导线及四分裂导线的气动力系数。何蔚超等［12］计算了不同覆冰形状的导线在不同风速和攻角情况下的影响规律。Braun 等［13］采用流固耦合模型分析了双分裂、三分裂及四分裂导线的扰流场。吕翼等［14］对新月形与扇形覆冰单导线和三分裂导线的气动力特性进行了数值模拟计算。

本文利用数值模拟的方法对覆冰导线绕流流场进行研究。首先考察了数值模拟技术在一定程度上代替风洞试验的可行性，将覆冰导线的气动力参数计算结果与实验结果进行了对比分析，验证了计算模型的精度。然后计算了四分裂导线在全攻角下的阻力系数、升力系数、扭矩系数的变化规律，分析了覆冰形状、覆冰厚度、来流风速对覆冰导线气动力系数的影响，并计算分析了导线间距与直径比对尾流的影响，所得空气动力参数可为导线舞动研究提供载荷支持。

1 气动力计算模型

采用湖北省中山口三分裂覆冰导线模型，扇形覆冰形状，将该导线结构的数值计算结果与风洞实验数据进行比较，验证该计算模型的精确度。

1.1 导线、间隔棒以及冰型参数

导线组成:钢芯铝绞股线，其中钢芯线37 ×φ2.6 mm，铝线42 × φ3.64 mm，密度:2.755 kg/m3;截面:圆形;直径:32.76 mm;导线综合拉伸弹性模量E:10 300 kg/mm2。

三分裂导线的3 根子导线用等边三角形间隔棒隔离、定位。间隔棒的几何尺寸如图1 所示，质量为9.1 kg。

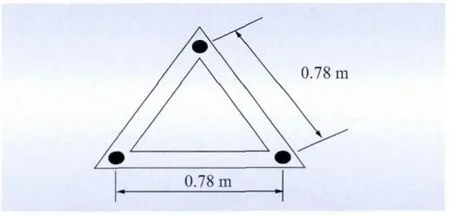
图1 间隔棒尺寸Fig.1 Size of spacer

如图2 所示，d 为导线直径，h 为冰型厚度;扇形冰型ABCD 由圆弧AB、CD 和直线AD、BC 围成，其中圆弧AB 和CD 为同心圆弧，圆弧AB 的圆心角为140°，圆弧CD 的圆心角为120°。

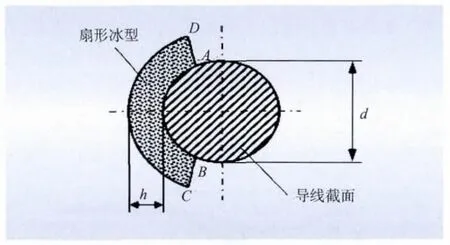
图2 扇形冰型Fig.2 Fan-shaped type ice

1.2 数据处理与对比分析

经过计算得到导线直径为32.76 mm、冰厚为18 mm的扇形冰型导线，在来流风速为14 m/s 工况下的气动力参数。中山口三分裂导线气动力参数实验值与数值解的对比曲线，如图3 ～5 所示。

由图3 ～5 三分裂导线数值解与实验值的对比分析可知:数值解与实验解的气动力曲线基本重合，仅仅是图3 的阻力系数在150°以后偏差比较大。但是由于风攻角一般不会大于150°，因此该计算模型可靠，误差在控制范围以内，可以将该数值模拟方法推广到更多导线气动力系数的数值计算中。

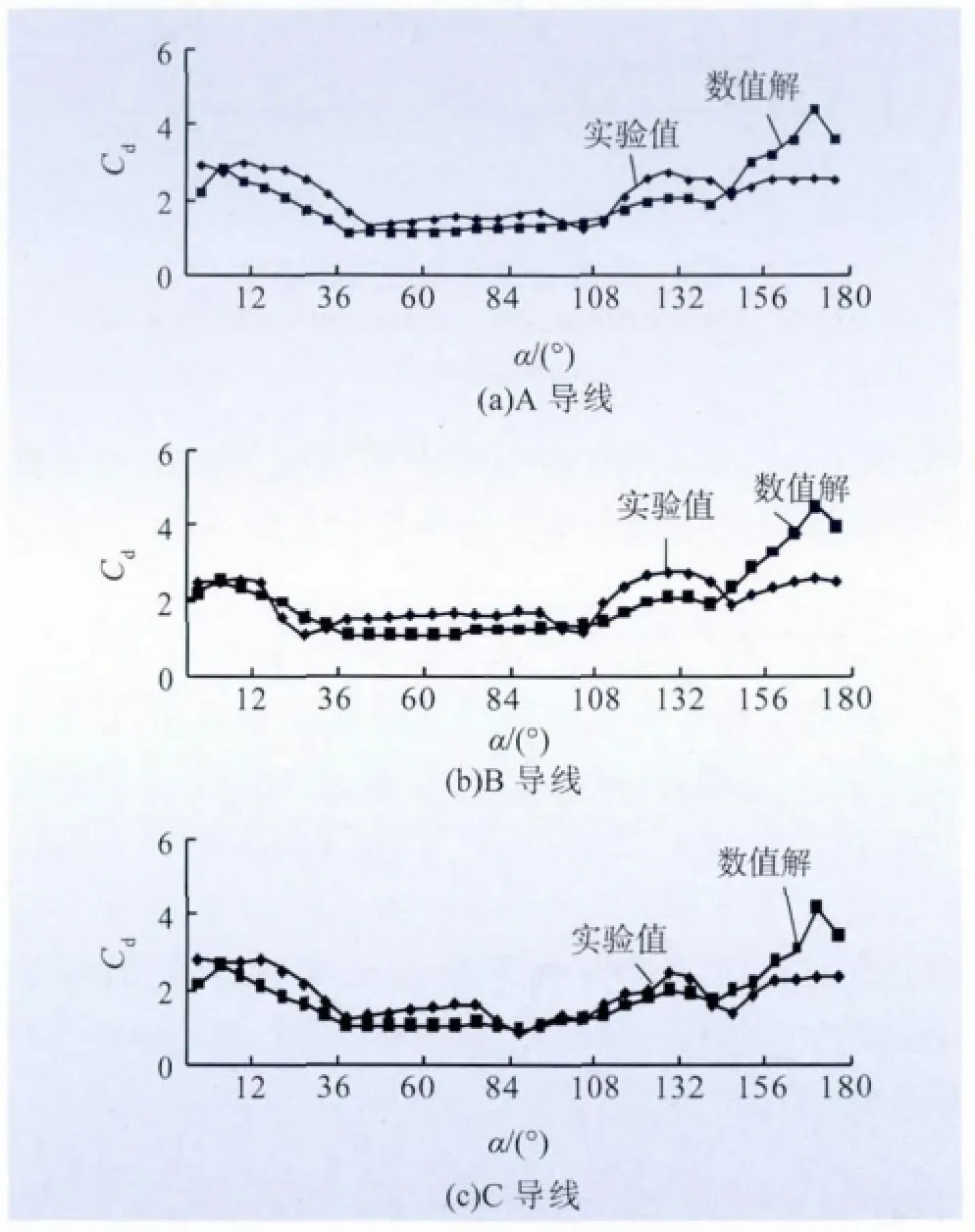
图3 阻力系数对比曲线Fig.3 Comparison curve of drag coefficient

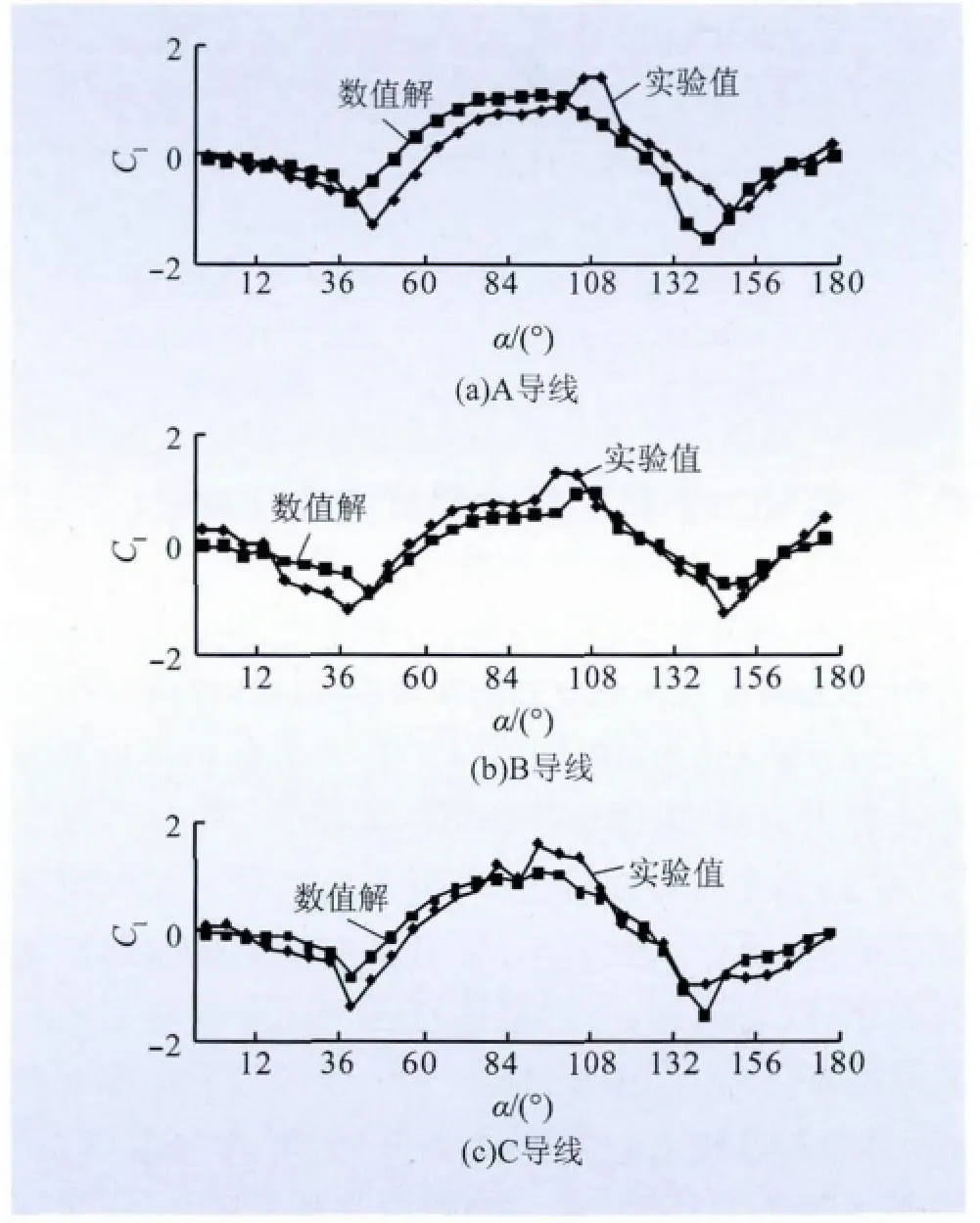
图4 升力系数对比曲线Fig.4 Comparison curve of lift coefficient

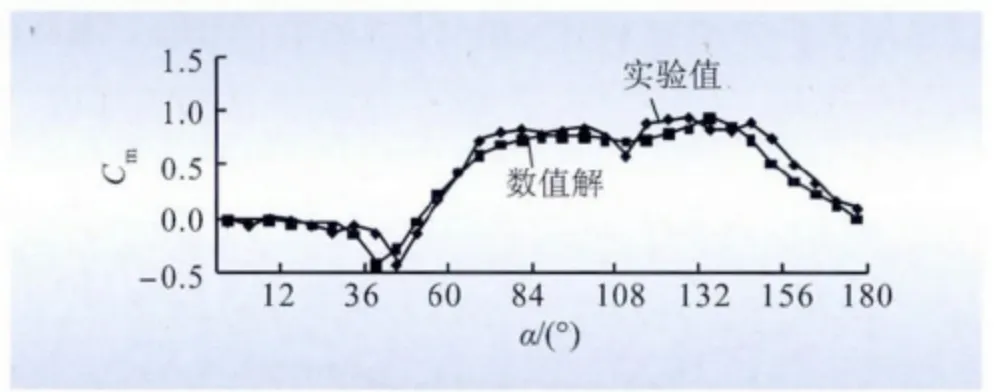
图5 A 导线扭转系数对比曲线Fig.5 Comparison curve of torsion coefficient of conductor A

2 气动力参数规律

图6 为新月形覆冰导线的横截面示意图，d 为导线直径，h 为覆冰厚度，新月形冰型ABCD 由半圆弧ABC 和半椭圆弧ADC 围成，半椭圆的短轴即为导线的直径d，长半轴为d/2 +h。图7 为D 形覆冰导线横截面示意图，d 为导线直径，h 为覆冰厚度，D 形冰型ABC 由半圆弧ABC 和直线AC 围成，其中AC 为D形半圆的直径，其大小为2(d+h)。

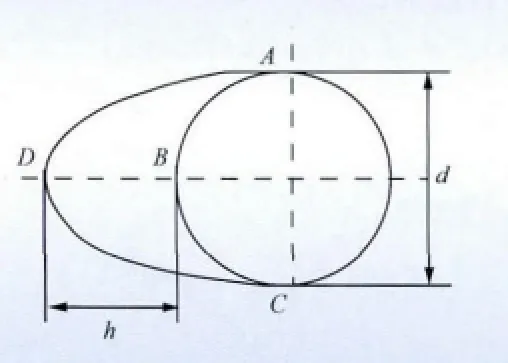
图6 新月形冰型Fig.6 Drescent-shaped type ice

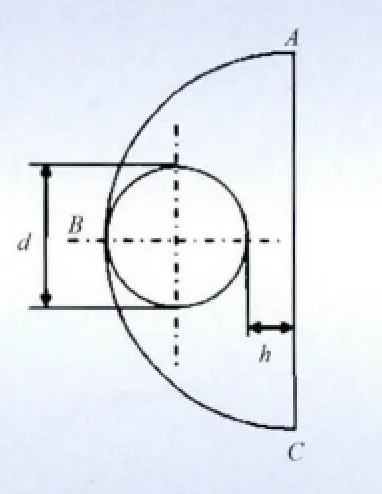
图7 D形冰型Fig.7 D-shaped type ice

2.1 气动力系数随覆冰厚度的变化规律

选取4×LGJ400/35 型新月形覆冰导线，来流速度为10 m/s 的其中一根子导线(A 子导线)在冰厚分别为5，10，15 mm 工况下的气动力系数数据进行分析。

(1)覆冰厚度对阻力系数、升力系数和扭矩系数均有较大影响，但影响规律不尽相同。

(2)由图8 可以看出，当风攻角为0° ～30°，覆冰厚度越大，阻力系数越小;阻力系数随着攻角的增加而增加;攻角越大，不同覆冰厚度工况下的阻力系数差异越来越小。当风攻角为30° ～150°，覆冰厚度越大，阻力系数越大。当风攻角趋于30°或135°时，不同覆冰厚度工况下的阻力系数差异越来越小;当风攻角为150° ～180°，覆冰厚度越大，阻力系数越小;阻力系数随着攻角的增加而减小;攻角越大，不同覆冰厚度工况下的阻力系数差异越来越大。

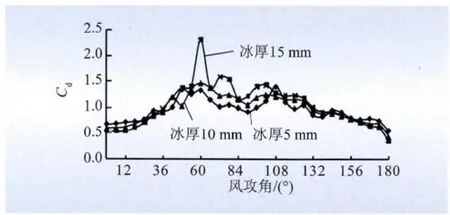
图8 阻力系数与覆冰厚度的关系Fig.8 Relationship between drag coefficient and ice thickness

(3)由图9 可以看出，当风攻角为0° ～120°和150° ～180°，覆冰厚度越大，升力系数越大;当风攻角趋于0°、120°、150°或180°时，不同覆冰厚度工况下的升力系数差异越来越小;当风攻角为120° ～150°，不同覆冰厚度下的升力系数近似相等，无明显差别。

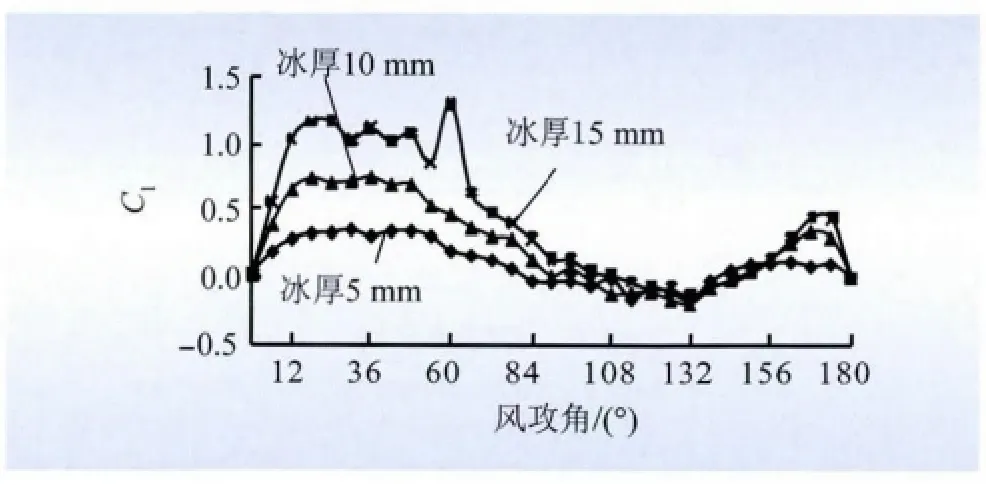
图9 升力系数与覆冰厚度的关系Fig.9 Relationship between lift coefficient and ice thickness

(4)由图10 可以看出，风攻角为0° ～180°，覆冰厚度越大，扭矩系数的绝对值越大;风攻角为0° ～108°，覆冰厚度对扭矩系数的影响较大，且攻角趋于0°或108°时，不同覆冰厚度工况下的扭矩系数差异越来越小;风攻角为108° ～180°，覆冰厚度对扭矩系数的影响不明显。

图10 扭转系数与覆冰厚度的关系Fig.10 Relationship between torsion coefficient and ice thickness

2.2 气动力系数随覆冰形状的变化规律

选取导线型号为4 ×LGJ400/35，冰型分别为新月形、D 形及扇形的覆冰分裂导线，在冰厚为10 mm，来流速度为10 m/s 工况下的其中一根子导线(A 子导线)的气动力系数数据进行分析，计算结果见图11 ～13所示。

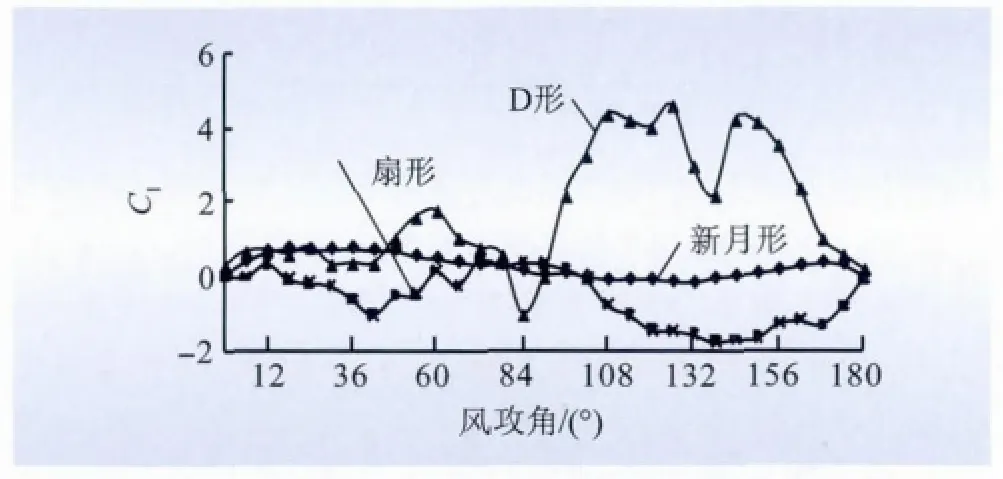
图11 升力系数与覆冰形状的关系Fig.11 Relationship between lift coefficient and ice shape

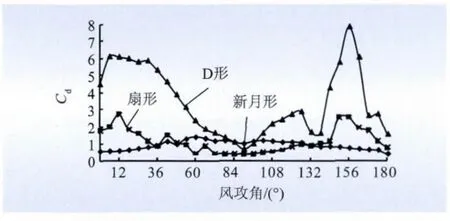
图12 阻力系数与覆冰形状的关系Fig.12 Relationship between drag coefficient and ice shape

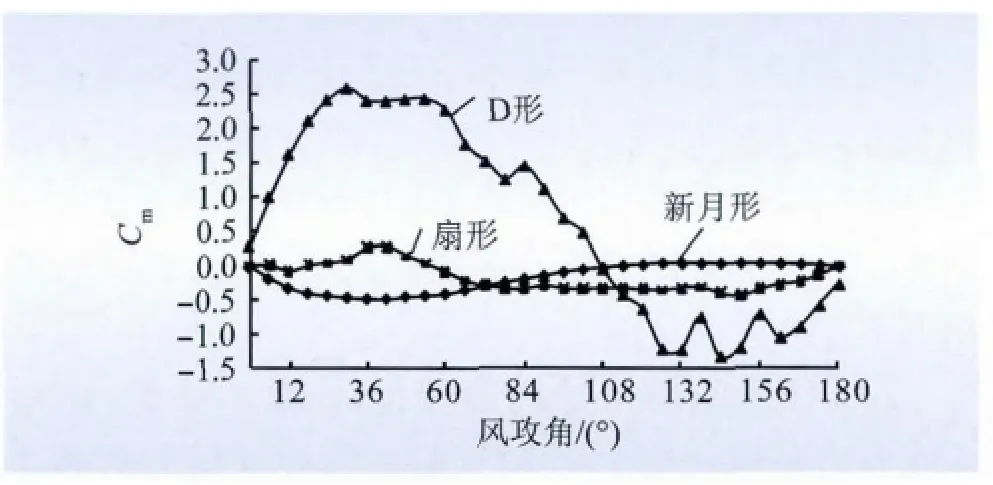
图13 扭矩系数与覆冰形状的关系Fig.13 Relationship between torque coefficient and ice shape

(1)由图11 ～13 可知，D 型冰型的气动力系数明显比其他2 种冰型大，原因在于相同导线直径的情况下，由图2、图6 及图7 的几何构型可以看出，D 型的总体几何尺度比另外2 种冰型大。

(2)由图11 ～13 可以明显地看出不同冰型，气动力系数随着风攻角的变化规律不尽相同。其原因在于覆冰导线属于工程结构剖面，描述非定常气动力的最有意义的系数是Strouhal 数，对于特定冰型的覆冰导线，Re 数对流动的图像几乎没有影响，因为气流在尖点处几乎立即分离，涡激气动力与Strouhal 数之间的关系没有规律，即与来流风速之间也没有规律，只能对具体剖面进行实验确定，不同的剖面会表现出不同的规律。

(3)根据图13 还发现4 ×LGJ400/35 扇形的扭转系数随风攻角的变化规律与湖北中山口三分裂导线的变化规律不尽相同，主要体现在96°到150°这一段的变化规律。其原因在于导线的几何构型对于扭转系数影响比较大，中山口分裂导线的冰厚为25 mm，4 ×LGJ400/35 导线的冰厚为10 mm，相差甚远，会在某特定角度范围表现不同的规律。

2.3 气动力系数随来流风速的变化规律

选取4 ×LGJ400/35 型新月形覆冰导线，覆冰厚度为10 mm 的其中1 根子导线(b 子导线)，在风速分别为7，10，15 m/s 工况下的气动力系数数据进行分析，计算结果见图14 ～16。

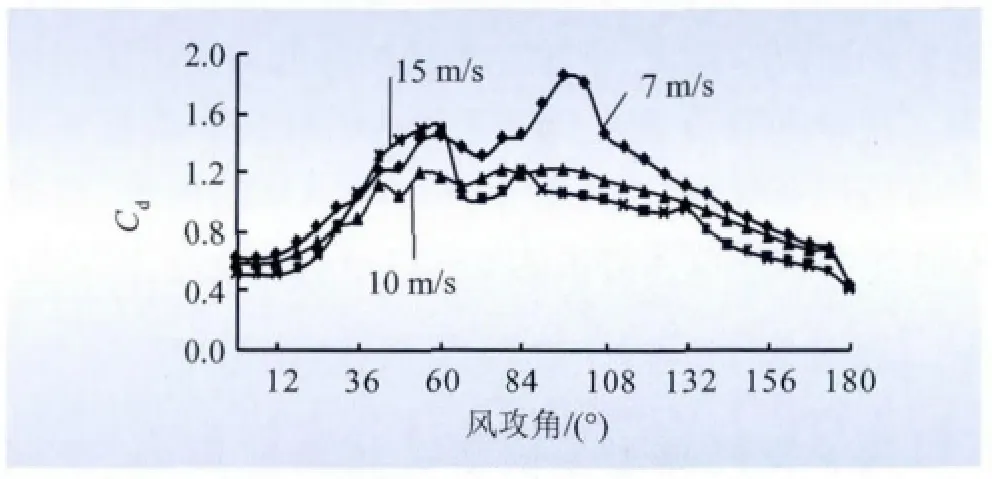
图14 阻力系数与风速的关系Fig.14 Relationship between drag coefficient and wind velocity

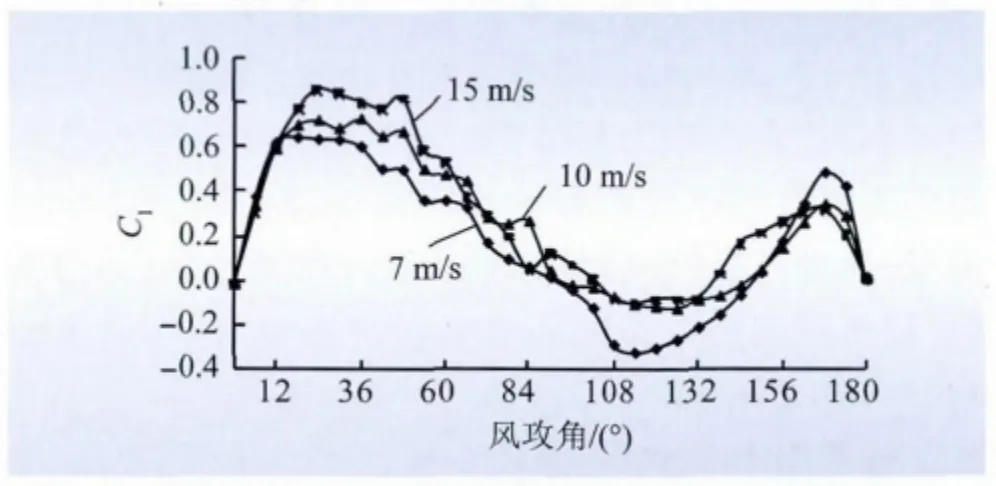
图15 升力系数与风速的关系Fig.15 Relationship between lift coefficient and wind velocity

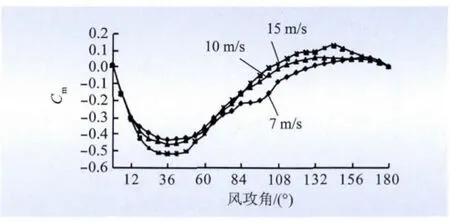
图16 扭矩系数与风速的关系Fig.16 Relationship between torque coefficient and wind velocity

(1)由图14 可以看出，来流风速对阻力系数有较大影响;在一定覆冰厚度下，当风攻角在0° ～180°的大部分区域内，风速越大，阻力系数越小;随着来流风速增加，不同风速下阻力系数的差异越来越小;同时随着风速的增加，出现波峰的位置向小角度偏移。

(2)由图15 可以看出，来流风速对升力系数的影响不明显，在v =7 m/s 到v =15 m/s 的数值模拟风速范围内，升力系数曲线在大部分攻角下是相似的。在风攻角为12° ～42°、162° ～174°时达到波峰，在108° ～138°时达到波谷。升力系数由正到负呈波状变化，随着风速增加，出现负升力系数的区间逐渐缩小。

(3)由图16 可以看出，来流风速对扭矩系数的影响不明显，在v =7 m/s 到v =15 m/s 的数值模拟风速范围内，扭转系数曲线在大部分风攻角下是相似的。同时风速越大，出现正扭转系数的风攻角区间越大。扭转系数分别在风攻角为45°和135°附近达到波谷值和波峰值，这是由于在以上风攻角附近，扭矩相比于其他风攻角处更大。

3 部分覆冰导线前后尾流影响分析

为了研究覆冰导线前后尾流的影响，选取4 ×LGJ400/35Y1007工况下的气动力系数数据进行分析。

针对新月形四分裂导线在攻角为45°工况下(导线直径为20 mm，冰厚为10 mm，来流风速为10 m/s)进行气动力系数的计算，通过改变导线的间距来研究气动力系数和导线间距与导线直径之比的关系，分析处于上风位和尾流中心区导线的气动力系数，归纳总结尾流对气动力系数的影响，计算结果如图17 ～19 所示。

分析图17 ～19 可知:

(1)导线间距与导线直径之比越小，前后导线的气动力系数相差越大。

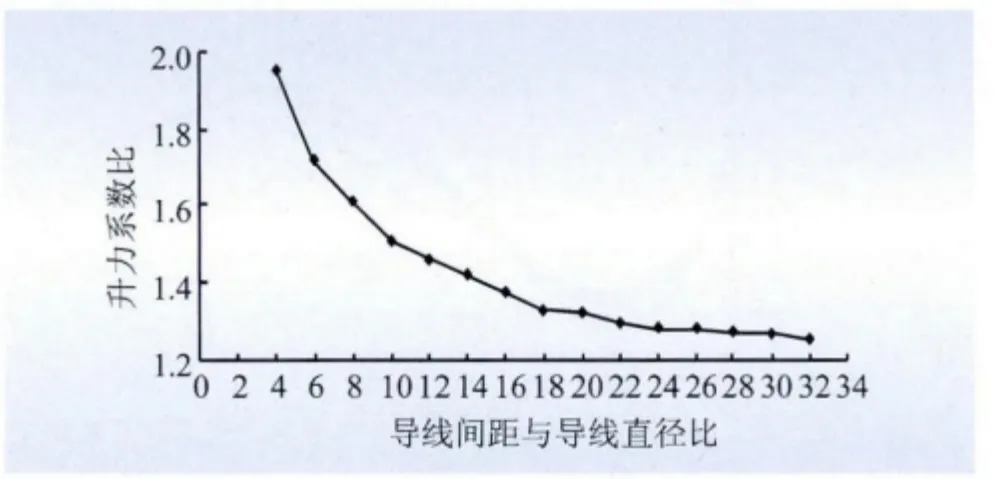
图17 前后导线升力系数比Fig.17 Lift coefficient ratio of front and rear wire

图18 前后导线阻力系数比Fig.18 Drag coefficient ratio of front and rear wire

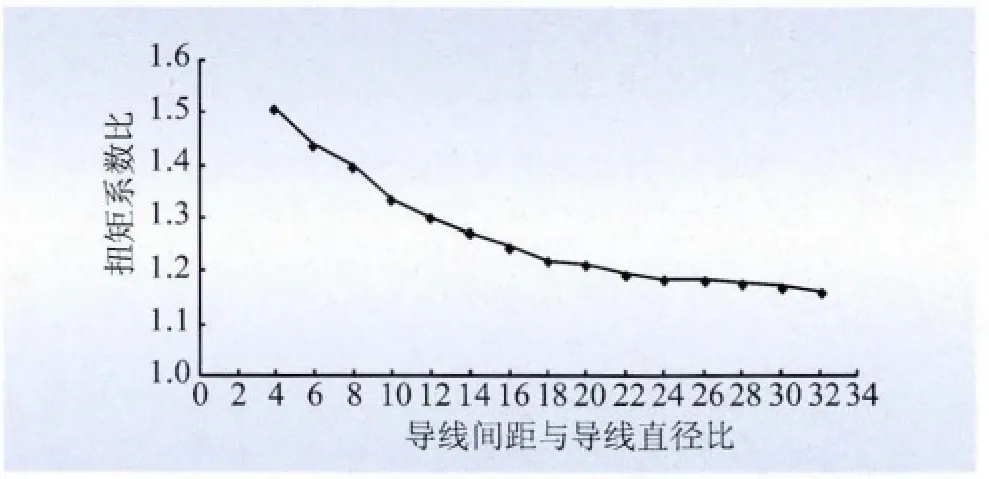
图19 前后导线扭矩系数比Fig.19 Torque coefficient ratio of front and rear wire

(2)当导线间距与导线直径之比达到一定程度时，前后导线的气动力系数之比就会越来越趋近于1的附近。即只要导线间距远大于导线直径时，尾流对导线气动力系数的影响较小，在可以接受的范围内可以忽略不计。

(3)由以上气动力系数变化曲线可知，导线间距与导线直径之比在0 ～20 时，前后导线之间的尾流影响较大，气动力系数相差较大，这时分裂导线不能用单导线的结果代替;当导线间距与导线直径之比大于20 时，前后导线的气动力系数比趋于平缓，并会逐渐趋近1 左右。

(4)导线间距与导线直径比为20 ～32 时，前后导线升力系数比趋于1.253，前后端导线阻力系数之比趋于1.141，前后导线扭转系数之比趋于1.160。由此可以得出阻力系数受尾流影响最不敏感，升力系数受尾流影响最敏感，扭转系数介于二者之间。

(5)虽然导线间距足够大，但是前后子导线的各气动力系数比并未完全等于1，还存在10% ～20%的差别。分析其原因，主要是因为位于上风位的子导线产生的涡脱落之后随流场往下游周期交替并逐渐减弱，当到达位于尾流中心区的子导线时，脱落涡并没有完全衰退，会对后方位于尾流中心区的子导线气动力系数产生影响。

4 结 论

(1)覆冰厚度对空气动力系数有较大影响。风攻角为0° ～180°，覆冰厚度越大，阻力系数、升力系数和扭矩系数的绝对值越大。

(2)来流风速对阻力系数有一定影响，在7 ～15 m/s风速时，风速越大，阻力系数越小，随着来流风速的增加，不同风速下阻力系数的差异越小;升力系数及扭矩系数受来流风速的影响较小，在7 ～15 m/s风速时，升力系数和扭矩系数曲线在大部分攻角下是相似的。

(3)导线的覆冰形状对气动力系数有很大的影响，在相同冰厚及来流风速条件下，气动力系数随着D 形覆冰、扇形覆冰、新月形覆冰依次大幅降低，且气动系数曲线的波动性依次降低。

(4)导线型号对气动系数也有一定程度的影响，对于新月型覆冰的5 种不同型号的导线，导线直径越大，升力系数、扭矩系数的绝对值越小;导线直径越大，阻力系数越小。

(5)在大部分风攻角范围内，分裂导线中各子导线的气动力系数随风攻角变化曲线与单导线基本相似;只是在某些风攻角下，流场后方子导线位于前方子导线的尾流影响区内时，气动系数存在一定差异。

(6)阻力系数受尾流影响最不敏感，升力系数受尾流影响最敏感，扭转系数介于二者之间。导线间距与导线直径比在20 ～32 时，前后导线升力系数比趋于1.253，前后端导线阻力系数之比趋于1.141，前后导线扭转系数之比趋于1.160。导线间距与导线直径之比在0 ～20 时，前后导线之间的尾流影响较大，其气动力系数相差较大。导线间距与导线直径比达到一定程度时，前后导线的气动力系数比就会越来越趋近于相同，即只要导线间距远大于导线直径时，尾流对导线气动力系数的影响较小，在可以接受的范围内可以忽略不计。

［1］Nigol O，Clarke G J． Conductor galloping and control based on torsional mechanism［C］//IEEE Power Engineering Society Winter Meeting，1974:74016-2．

［2］Chadha J，Jaster W． Influenee of turbulence on the galloping instability of iced conductors［J］． IEEE Transactions on Power Apparatus and System，1975，94(5):1489-1499．

［3］Stumpf P，Ng H C M． Investigation of aerodynamic stability for selected inclined cables and conductor cables［D］．Canada:University of Manitoba WinniPeg，1990．

［4］Ishihara T A．Wind tunnel study on aerodynamic characteristics of ice accreted transmission lines［C］//5thInternational Colloquium on Bluff Body Aerodynamics and Applications，Ottawa，2004:369-372．

［5］李万平，杨新祥，王海期，等． 大跨越覆冰导线空气动力学特性的测试［J］．超高压输变电运行技术，1990(8):95-107．

［6］顾明，马文勇，全涌，等．两种典型覆冰导线气动力特性及稳定性分析［J］．同济大学学报:自然科学版，2009，37(10):328-332．

［7］马文勇，顾明，全涌，等． 准椭圆形覆冰导线气动特性试验研究［J］．同济大学学报:自然科学版，2010，38(10):1409-1413．

［8］张雁宏，严波，周松，等． 覆冰四分裂导线静态气动力特性试验［J］．空气动力学学报，2011，29(2):150-154．

［9］肖正直，晏致涛，李正良，等． 八分裂输电导线结冰风洞及气动力特性试验［J］．电网技术，2009，33(5):90-94．

［10］蔡萌琦，严波，吕欣，等，覆冰四分裂导线空气动力系数数值模拟［J］．振动与冲击，2013，32(5):132-137．

［11］林巍．覆冰输电导线气动力特性风洞试验及数值模拟研究［M］．杭州:浙江大学，2012．

［12］何蔚超． 架空输电线路舞动气动参数模拟及在线监测技术研究［M］．南京:南京理工大学，2013．

［13］Braun A L，Awruch A M． Aerodynamic and aerolastic analysis of bundled cables by numerical simulation［J］． Journal of Sound and Vibration，2005，284(1-2):51-73．

［14］吕翼，楼文娟，孙珍茂，等，覆冰三分裂导线气动特性的数值模拟［J］．浙江大学学报:工学版，2012，44(1):175-179．